Lévy 稳定过程均值变点监测在EWMA 和GLR控制图中的比较
胡松瀛,李 泰
(亳州学院 电子与信息工程系,安徽 亳州 236800)
为优化自动系统的自动故障监测,工业生产中的质量控制等功能,就要解决在随机系统中如何快速的监测出变点.为了快速监测出变点,就产生了不同的控制图,例如:Shewhart[1]控制图、EWMA[2]控制图、CUSUM[3-4]控制图、Cuscore[5-6]控制图和GLR[7]控制图.一些研究是基于随机变量服从正态分布,或方差有限[8-9].在实际问题中,大量的变量是服从稳定分布的,有无限方差,例如:年降雨量、刻画核反应堆温度的温度分布、股票市场的收益率及金融网络中的资金交易量,这些都是Lévy 稳定过程,可见研究Lévy 稳定过程均值变点具有十分重要的意义.在统计过程控制中,通过计算平均运行长度,考量控制图监测均值变点的效果.笔者首先探讨了控制图EWMA、GLR 的平均运行长度的估计,其次分析了数字模拟比较.
1 预备知识
首先给出4 个定理[7],利用这4 个定理得到其他定理.
依照规定,水行政执法机关一旦发现涉水违法行为可能触犯刑法,有义务将相关案件移送至公安、检察等司法机关处理。按照最高检规定,水行政执法机关向公安机关移送案件,公安机关作立案、不立案决定处理,应向同级检察院备案。但对未报送检察机关备案的,没有规定监督和惩罚措施,这使得部分水行政执法机关对应移送的案件持一种消极态度。虽然刑法第402条规定了行政执法机关不移送案件的刑事责任,但该条款的适用取决于检察机关及时发现行政机关在移送案件过程中的渎职行为。事实上在未及时备案又缺乏信息共享的前提下,检察机关很难发现部分水行政执法机关的渎职行为。

定理2 若ξ~Sα(p,q,μ),r是实常数,则:ξ+r~Sα(p,q,μ+r).
定理3 随机变量ξ~Sα(p,q,μ),k∈R,k≠0,有:


由此(2)式的向下不等式得证.下面证明(2)式的向上不等式.

定理6 设稳定过程的第i(i=1,2,…)个观测值是ξi,ξi~Sα(1,0,μi)且相互独立,1<α≤2,μi≥0,令μ0=inf[μi],μ0=sup[μi],,对于EWMA 控制图,有:
下面证明(3)式的向下不等式.
由于ξm(i=1,2,…)是相互独立的一列随机变量,根据定理4,有:
2 平均运行长度ARL 的估计
由于ξm(i=1,2,…)是相互独立的一列随机变量,根据定理4,有:


设ξi,i=1,2,…,n,是独立稳定随机变量序列,考虑检验问题:

定理5 证毕.
其中变点o未知,μ0≠μ,α∈(0,2],q∈[-1,1],p≥0.
目前,人工智能技术还处于初级阶段。对于人工智能技术能达到何种水平,存在分歧。乐观者,如人工智能科学家加里斯认为,人工智能的智力是人类的万亿个万亿倍(10的24次方)。在21世纪末,量子计算机的计算能力可能是当代计算机的万亿个万亿个万亿倍(10的36次方)。①这种人工智能可以称为“超人”。届时,人类与超人的智力差距,比细菌与人类的智力差距还大。但是,并非所有人工智能科学家都赞同加里斯的技术乐观(不是社会效应乐观)态度。

估计EWMA 和GLR 控制图的平均运行长度之前,对一些符号先做出说明,没有均值变化的概率和期望用P(·)和E(·)表示.ARL0表示受控平均运行长度,ARLμ表示失控平均运行长度,且:ARL0(T)=E(T),ARLμ(T)=Eμ(T).其中T表示的是过程失控时的预警时间.考虑实际情况,c取充分大.

(3)式的向上不等式得证.
为了检验过程中均值有没有变点,需要利用假设检验(1)式.假设在过程中变点没有出现,那么接受H0;否则接受HA.在HA情况下,从时刻o开始,过程均值产生漂移μ-μ0.若μ>μ0,就是向上漂移,若μ<μ0,就是向下漂移.不论是双向飘移,还是向下漂移,它们的监测与上漂移的监测没有本质区别,笔者仅就向上漂移的监测作出探讨.

MONARCH-2[11]是一项Ⅲ期、双盲临床研究,入组了669例HR+和HER2-的晚期乳腺癌患者,按2∶1的比例随机分为接受abemaciclib(150 mg,2次/d,持续给药)或安慰剂联合氟维司群治疗组。结果显示,abemaciclib组和安慰剂组的mPFS分别为16.4个月和9.3个月(HR=0.553,95% CI:0.449~ 0.681,P< 0.001)。
从孔子“礼”的发生机制来看,礼必须具有能指导主体实践的功能。前文提到,孔子之“礼”是在周礼实践基础上之改造再实践。礼的核心内容包含了对人伦关系的规定。孔子强调,仁是礼的核心内涵,所以礼的内容主要着眼于仁的约制规范和实践。孔子主要从以下两个方面进行对于礼的规制的:其一是处于特殊的身份、地位的道德实践主体拥有不同的道德实践义务与原则,其一是作为一般普遍意义上而言的道德实践主体又必须必须具有共同的行为准则。
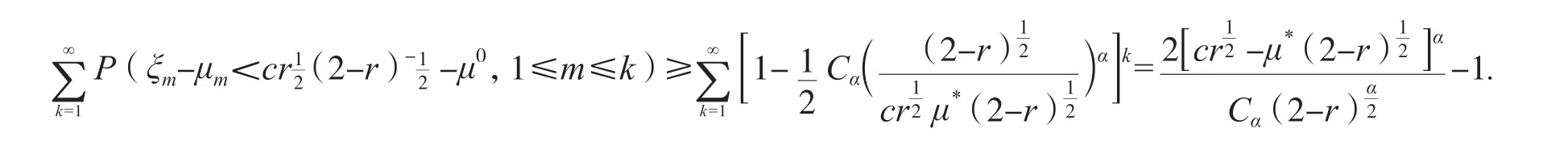
定理6 证毕.
3 数字模拟
检验控制图效果的一个标准是平均运行长度ARL0,在受控的前提下,并且ARL0以及均值漂移μ相等,需要比较失控状态时的平均运行长度ARLμ,ARLμ小的控制图的效果就是较优的.这里仅就σi=1.5 和σi=1.8 时,比较EWMA 和GLR 这两种控制图的平均运行长度ARLμ.表1 和表2 给出了EWMA 和GLR 这两种控制图在Xi~S1.5(1,0,μ)和Xi~S1.8(1,0,μ)状态下的平均运行长度.模拟的结果是由多次重复试验获得,其中随机变量序列Xi~Sαi(1,0,μ)是由rstalbe 程序生成的.
第一,构建了完备的法律体系。美国早在1965年起,为了能够为老年人的医疗、救助、安养机构提供法律保障,出台了《多目标老人中心方案》、《老年法》等法律。其次,建立完善的养老金制度。由于美国强大的养老金制度的支持,使得市场力量能够大量引入美国养老机构中。

表1 Xi~S1.5(1,0,μ)情况下两种控制图平均运行长度的比较

表2 Xi~S1.8(1,0,μ)情况下两种控制图平均运行长度的比较
4 分析数据
从表1 可以看出,在α=1.5 稳定分布中,GLR 的效果明显比EWMA 的好.从表2 可以看出,在α=1.8稳定分布中,当r<0.1 时,EWMA 的效果明显比GLR 的好;r=0.1 两者的效果相差不大,随着r的增大,EWMA 的效果不如GLR 的效果.

