统计学专业数理统计课程研究性教学之初探*
——非正态总体参数的区间估计
姜培华,汪晓云,朱五英
(安徽工程大学数理与金融学院, 安徽 芜湖 241000)
引言
数理统计是一个有着广泛应用的数学分支,而参数估计又是数理统计的重要内容之一,它包括点估计和区间估计.与未知参数的点估计相比,区间估计有着明显的优势;它不仅给出了参数真值所在的范围,还给出了该范围包含参数的可信程度.对于正态总体参数的区间估计问题各类教材都有非常详尽的介绍,如文献[1]和[2],但对非正态总体参数的区间估计讨论较少.文献[3]和[4]通过实例介绍了一般总体构造其分布中未知参数区间估计的枢轴量法和分布函数法.文献[5-7]研究了对一般总体构造其分布中未知参数近似区间估计的方法.文献[8-10]基于枢轴量法和大样本方法研究了几种非正态离散总体参数的精确区间估计和近似区间估计问题.本文对非正态总体构造未知参数区间估计的常用方法进行全面梳理和总结,并通过实例来呈现如何使用这些方法来分析求解未知参数的置信区间,以方便学生系统掌握和教师课堂讲授.
1 相关知识
定义1[1]设θ∈Θ是总体的一个参数,(x1,x2,…,xn)为来自该总体的简单随机样本,如果对于给定的
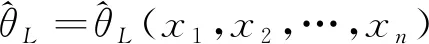
引理1[1]若随机变量X服从均匀分布,即X~U(0,1),则有
1)随机变量Y=1-X服从均匀分布,即Y~U(0,1);
2)随机变量Z=-2lnX服从卡方分布,即Z~χ2(2).

定理1设总体X服从分布F(x,θ),x1,x2,…,xn为来自该总体的简单随机样本,则有
证明因x1,x2,…,xn为来自总体F(x,θ)的简单随机样本,由引理2知:F(xi,θ)~U(0,1),
1-F(xi,θ)~U(0,1),基于引理1再利用卡方分布的可加性可知结论成立.
定理2设总体的密度函数为f(x),xp分为其p分位数,f(x)在xp处连续且f(xp)>0,则当
n→+∞时,样本p分位数mp的渐近分布为
特别地,对样本中位数,当n→+∞时,近似地有
此定理的证明可参见文献[1],这里不再赘述.
2 区间估计的构造方法
2.1 枢轴量法
枢轴量法是构造非正态总体未知参数θ的置信区间的最常用方法之一,下面简要给出通过构造枢轴量进行区间估计的步骤:
1)设法构造一个样本和参数θ的函数G=G(x1,x2,…,xn,θ)使得G的分布不依赖于未知参数,一般称具有这种性质的G为枢轴量.
2)适当地选择两个常数c和d,使得对给定的α∈(0,1),有P(c≤G≤d)=1-α成立,在离散场合上式等号改为大于等于.

对未知参数进行区间估计的关键在于构造合适的枢轴量并确定其所服从的概率分布,然后根据相应的分位数得到所需要的概率表达式.枢轴量的好坏不仅影响求解的速度,更重要的是对置信区间的优良性有着直接的影响.下面通过一些具体实例说明如何选择一个合适的量来构造枢轴量,进而得到相对优良的置信区间.
例1(基于充分统计量构造枢轴量) 设总体X服从拉普拉斯分布,其密度函数为
其中参数θ未知,求θ的水平为1-α的等尾置信区间.
解: 样本的联合密度函数为
对上述分布函数,利用变限积分函数求导可得其密度函数
从而可知
利用卡方分布的可加性可得枢轴量
基于枢轴量G可求得参数θ的1-α水平的等尾置信区间为
例2(基于充分统计量构造枢轴量) 设总体X服从幂分布,其密度函数为
f(x,θ)=θxθ-1,0
其中参数θ未知,求θ的水平为1-α的等尾置信区间.
解: 样本的联合密度函数为

对上述分布函数,利用变限积分函数求导可得其密度函数
从而可知
利用卡方分布的可加性可得枢轴量
基于枢轴量G可求得参数θ的1-α水平的等尾置信区间为
例3(基于顺序统计量构造枢轴量) 设总体X的密度函数为
f(x,θ)=e-(x-θ),x>θ,θ∈R.
其中参数θ未知,试求:
1)参数θ的水平为1-α的最短置信区间;
2)参数θ的水平为1-α的等尾置信区间.
解: 1)令yi=xi-θ,i=1,2,…,n,则y1,y2,…,yn独立同分布于指数分布Exp(1).y(1)的密度函数为
g(y)=ne-ny,y>0.
即x(1)-θ的分布与θ无关,其密度函数为g(y)=ne-ny,y>0,因此可以构造枢轴量G=x(1)-θ来求解置信区间.



例4(基于顺序统计量构造枢轴量) 设x1,x2,…,xn为来自均匀分布U(θ1,θ2)的简单随机样本,记
x(1)≤x(2)≤…≤x(n)为其顺序统计量,其中参数θ1,θ2未知,求θ2-θ1的水平为1-α的等尾置信区间.
解: 令yi=(xi-θ1)/(θ2-θ1),i=1,2,…,n,则y1,y2,…,yn独立同分布于均匀分布U(0,1).首先可以求得(y(1),y(2))的联合密度函数为
f(y,z)=n(n-1)(z-y)n-2,0 记极差R=y(n)-y(1),则(y(1),R)的联合密度函数为 f(y,r)=n(n-1)rn-2,y>0,r>0,y+r<1. 于是可求得极差R的边际密度函数为 从而可知R服从贝塔分布,即y(n)-y(1)~Be(n-1,2),所以有 P(Beα/2(n-1,2)≤y(n)-y(1)≤Be1-α/2(n-1,2))=1-α 枢轴量法求解区间估计的最大困难是如何寻找合适的枢轴量,该方法对概率统计基础要求较高,技巧性很强,比较灵活,因此构造合适的枢轴量非常困难,可谓是一种挑战.如果一个统计总体X,其分布函数F(x)有比较简洁的显式表达式且仅含有待估的参数,这时利用分布函数法构造区间估计比较有效,会达到“事半功倍”的效果.下面通过实际例子来展示分布函数方法的使用技巧. 例5(基于分布函数法) 设总体X服从幂分布,其密度函数为 f(x,θ)=θxθ-1,0 其中参数θ未知,求θ的水平为1-α的等尾置信区间. 解: 总体X的分布函数为 F(x,θ)=xθ,0 从而可以解出参数θ的1-α水平的等尾置信区间为 例6(基于分布函数法) 设总体X的密度函数为 f(x,θ)=e-(x-θ),x>θ,θ∈R. 其中参数θ未知,求参数θ的水平为1-α的等尾置信区间. 解: 总体X的分布函数为 F(x,θ)=1-e-(x-θ),x>θ,θ∈R. 从而可以解出参数θ的水平为1-α的等尾置信区间为 例7(基于分布函数法) 设总体X服从瑞利分布,其密度函数为 f(x,λ)=2λxe-λx2,x>0,λ>0. 其中参数λ未知,求参数λ的水平为1-α的等尾置信区间. 解: 总体X的分布函数为 F(x,λ)=1-e-λx2,x>0,λ>0. 从而可以解出参数λ的水平为1-α的等尾置信区间为 综上,对比枢轴量法和分布函数法,不难发现在某些情况下分布函数法和枢轴量法在构造区间估计方面具有一致性,二者是等价的.如例2和例5中关于幂分布参数θ的区间估计问题,枢轴量法和分布函数法最终所得的结果是一致的,但分布函数法明显优于枢轴量法,简便易行.在有些场合,分布函数法和枢轴量法所获得的区间估计具有明显的不同,区间估计的优劣也有差别.如例3和例6中,枢轴量法是仅依赖于样本的最小统计量,而分布函数法主要依赖于全样本. 在有些情形下,寻找枢轴量及其分布比较困难,分布函数法也很难凑效,这时可用渐近分布来构造近似的置信区间,如利用中心极限定理近似、极大似然估计的正态近似和样本分位数的正态近似等.下面通过实例来说明大样本近似方法的使用. 例8(中心极限定理近似) 设x1,x2,…,xn是来自泊松分布P(λ)的简单随机样本,其中参数λ未知,求参数λ的水平为1-α的近似等尾置信区间. 此u可作为枢轴量,对给定的显著性水平α,利用标准正态分布的分位数u1-α/2可得 上述关于λ的二次多项式的二次项系数大于零,故二次函数开口向上,其判别式 故此二次曲线和横轴有两个交点,记为λL和λU(λL<λU),则有P(λL≤λ≤λU)=1-α,其中λL和λU可表示为 故参数λ的水平为1-α的近似等尾置信区间为 事实上,上述近似区间是在样本容量n比较大时使用的,此时有 于是,λ的1-α水平的近似等尾置信区间可进一步简化为 例9(样本中位数正态近似) 设总体X的密度函数为 其中参数θ未知,x1,x2,…,xn是来自该总体的简单随机样本,求参数θ的水平为1-α的近似等尾置信区间. 解: 由于柯西分布关于θ对称,故θ是总体中位数.由定理2可知其样本中位数近似于正态分布,即 所以有 从而可知参数θ的1-α水平的近似等尾置信区间为 综上可知,一般在样本容量足够大的情况下,根据中心极限定理,非正态总体的抽样分布与正态总体的抽样分布差异较小,因此在大样本条件下,可以把非正态总体问题转化为正态总体问题,并近似地应用正态总体条件下导出的抽样分布公式,进而作出各类统计推断,这就是大样本统计推断原理,在区间估计中也遵循这一原则. 总之,非正态总体参数的区间估计一直是数理统计中的一个重点和难点,其处理方法灵活,技巧性强,学生难于掌握.本文系统归纳总结了处理非正态总体参数区间估计的三种常用方法,即枢轴量法、分布函数法和大样本方法.其中枢轴量法和分布函数法推导给出的置信区间都是精确的,大样本方法获得的置信区间都是近似的.通过具体的典型实例展示了使用三种方法构造置信区间的思路和技巧,使学生便于掌握和接受.文中的方法和处理技巧在数理统计研究性教学中值得借鉴和使用,能够让学生系统掌握求解非正态总体参数置信区间的常用方法和技巧,并能激发学生的学习兴趣和热情,增强其学习成就感.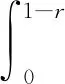
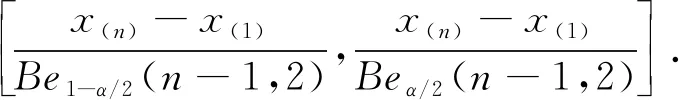
2.2 分布函数法
2.3 大样本方法
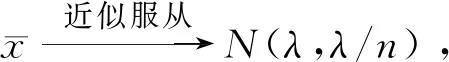
3 结语

