基于分数阶锂电池模型的FOMIAEKF算法SOC估计

丁羿茗，吕瑞强，蒋 超

（空军勤务学院，江苏徐州 221000)

荷电状态(SOC)作为锂电池特性的一个重要参数，它的精确估计对锂电池正常工作十分重要。传统的SOC计算方法依赖于电池自身特性，如开路电压法和安时积分法，智能估计算法有神经网络算法和扩展卡尔曼滤波算法。文献[1]采用基于数值优化的BP 神经网络(LM-BP)算法对SOC进行估算，提高了收敛速度。神经网络算法可以不需要锂电池模型进行估计，但是估算精度和样本的质量关系密切。文献[2]运用扩展卡尔尔曼滤波(EKF)估算锂电池SOC，减小了安时积分法的累积误差，但是它的近似非线性以及恒定的过程噪声会带来误差影响。文献[3]运用双卡尔曼滤波提高了估算SOC的精度，但是没有减小扩展卡尔曼滤波器近似非线性误差。文献[4]运用自适应扩展卡尔曼滤波算法修正了噪声恒定带来的误差，但是对历史新息数据没有充分利用。

本文在分数阶锂电池模型基础上，提出了多新息自适应EKF 算法，改进了EKF 滤波器过程噪声与观测噪声恒定所带来的的误差，充分利用了历史新息，通过联合估计实时修正模型参数。Matlab 仿真验证表明该方法可以有效提高SOC估算精度和跟踪速度。

1 分数阶锂电池模型

1.1 锂电池分数阶建模

关于分数阶微积分的定义有很多，本文用G-L 定义直接离散化分数阶微分方程，G-L 定义[5]如下：

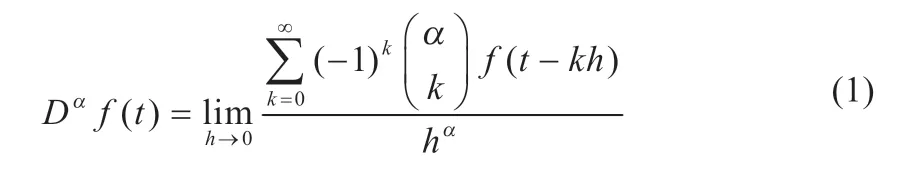
式中：α 代表方程的阶数，阶数的范围在(0,1)之间；h表示采样时间；k是整数。

使用分数阶理论进行锂电池建模[6]，可以反映极化、扩散和非线性因素带来的影响，提高模型的精度，锂电池的分数阶等效电路模型如图1 所示。VOCV是电池的开路电压，R0为电池内阻，R1、R2为纯阻性内阻，分数阶元件用CPE 表示，系数分别为C1、C2，分数阶阶次表示为α、β，取值范围是(0,1)，将理想电容元件用分数阶电容CPE 代替，可以更好地反映电极表面的弥散效应。

图1 分数阶等效电路模型

将VCPE1(t)、VCPE2(t)作为系统的状态，I0(t)作为系统的输入，系统的输出为VO(t)，分数阶电池模型的状态方程如下：

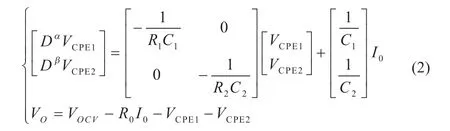
电容CPEI、电容CPE2用分数阶表示如下：

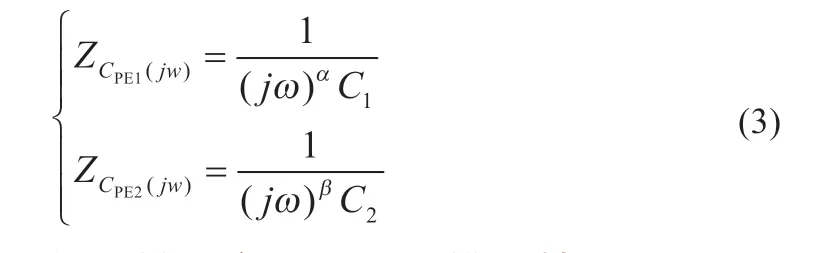
1.2 锂电池分数阶模型参数辨识及模型精度验证

遗传算法步骤如下：随机产生初值并转换为二进制代码，代表不同个体的二进制代码可以通过相互交换、独自变异[7]产生新个体。将二进制码解码后代入适应度函数，判断是否满足要求，当满足设定条件时停止[8]，适应性条件如式(4)所示：

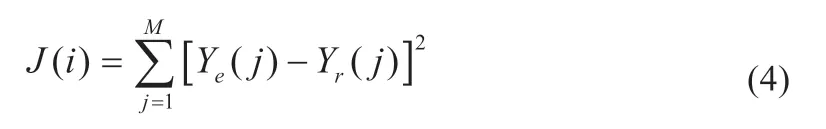
式中：Ye(j)是预测输出；Yr(j)是期望输出；M是被测数据组的长度。

遗传算法流程图如图2 所示。

图2 遗传算法流程图

一代种群中，个体的不同会导致适应度和遗传概率的不同，不同个体的交叉概率和变异概率可以表示如下：

式中：Jmin表示适应性条件的最小值，可以看出最优的个体概率均为0，J(i)的值越大，获得进化的机会越多。

自适应遗传算法(AGA)辨识出来的分数阶模型参数(R0、R1、R2、C1、C2)是整个脉冲放电过程的最优解，参数辨识结果如表1 所示。分数阶模型与整数解模型的误差对比如图3 所示，误差数据如表2 所示，分数阶模型的最大误差为0.037 5 V，平均误差为0.004 6 V，均优于整数阶模型。

表1 AGA 算法参数辨识结果

图3 分数阶模型与整数解模型误差对比

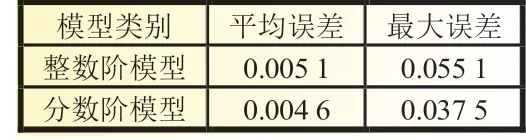
表2 模型误差对比 V

2 基于分数阶扩展卡尔曼滤波算法估计SOC

2.1 分数阶扩展卡尔曼滤波算法

EKF 算法可以处理非线性系统的问题，原理是将非线性系统的空间方程在xk处进行泰勒级数展开，只保留一阶项，得到近似的线性空间方程，对EKF 的状态变量，用G-L 定义求分数阶导数[9-10]，采样时间h取为1，得到如下表达式：

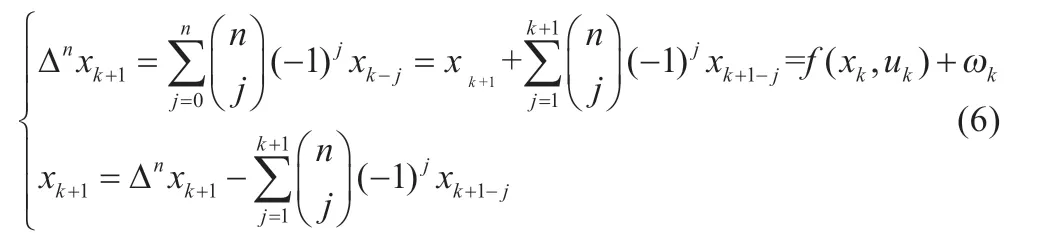
式中：Δ 是差分算子；n是阶数。

将式(2)分数阶模型表达式离散化，可得离散化分数阶锂电池模型表达式[11-12]：

基于分数阶模型，用EKF 算法估算锂电池SOC，运用Matlab 软件在城市循环工况(UDDS)下对算法进行仿真验证，结果如图4～5 所示，分数阶模型的引入使算法的精度得到了提高，整数阶EKF 算法因为模型精度问题，误差始终向一侧偏移，将模型更改为分数阶后，模型的精度提高，虽然在初始阶段，EKF 算法误差较小，但是随着时间的累计，分数阶扩展卡尔曼滤波(FOEKF)算法精度逐渐提高。经计算，EKF 算法估算SOC误差平均值为0.015 3，最大误差为0.033 3，FOEKF算法估算SOC误差平均值为0.011 2，最大误差为0.032 5。

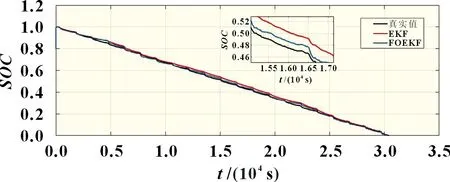
图4 FOEKF和EKF算法估算SOC曲线图

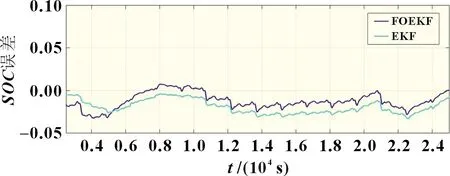
图5 FOEKF和EKF算法估算SOC误差对比图

2.2 分数阶多新息自适应扩展卡尔曼滤波算法

EKF 算法的状态噪声和观测噪声是恒定值，这会导致估计误差变大。自适应扩展卡尔曼滤波(AEKF)算法可以对新息或者残差进行实时监测，修正状态噪声和观测噪声。AEKF 算法过程如下：

式中：ek代表新息，若为则表示残差。

观测噪声方差Rk和状态噪声方差Qk的自适应过程如下：

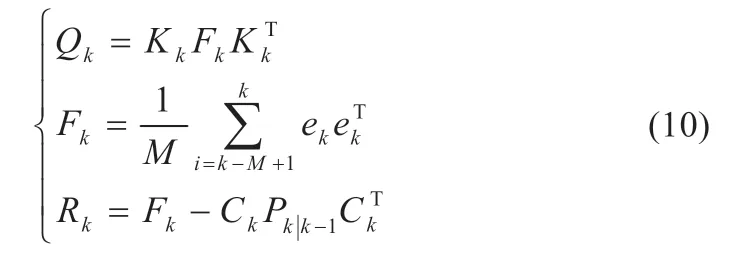
式中：Fk为新息的实时估计方差；M为滑动数据窗口长度[13]。

将多新息和EKF 算法结合，计算量会略有增大，但是精度得到了提高。将单新息ek扩展到新息矩阵，如下所示[14]：

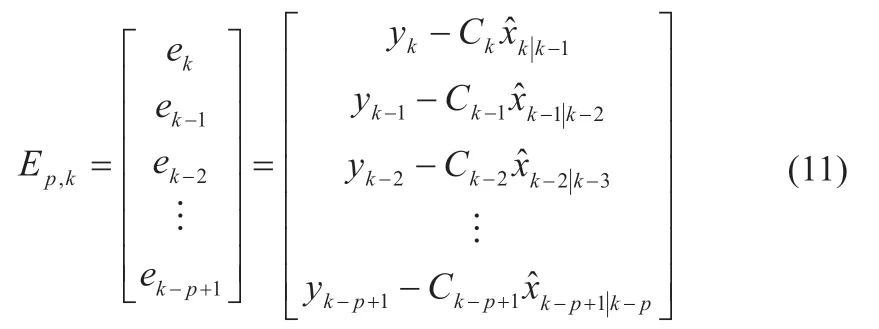
同时，将增益Kk也扩展成为增益矩阵，那么，状态向量的更新如下所示：

式中：Ki,k是k时刻的增益；Ep,k是新息矩阵；p是新息长度。

在UDDS 工况下，运用Matlab 软件对算法进行仿真验证，将AGA 算法辨识出来的参数代入模型中，仿真结果如图6～7 所示，仿真数据如表3 所示，分数阶多新息自适应扩展卡尔曼滤波(FOMIAEKF)算法估计误差的平均值和最大值都有所减小，说明该算法可以有效提高SOC估计精度。

图6 FOMIAEKF和FOEKF算法估算SOC曲线图

图7 FOMIAEKF和FOEKF算法估算SOC误差对比图

表3 FOEKF 与FOMIAEKF 算法估计SOC 误差对比

3 锂电池SOC 和健康状态联合估计

3.1 UKF 算法估计锂电池健康状态

用UKF 算法估算锂电池健康状态(SOH)，将电池容量C和电池内阻R0作为健康状态的估计量，UKF 算法估计流程首先确定状态值初始值x0和后验状态误差协方差初始值P0，计算采样点：

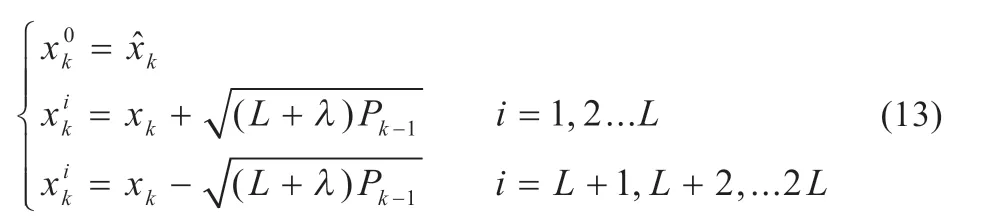
式中：L为状态向量的长度。

UKF 算法增益矩阵的更新如式(14)所示：

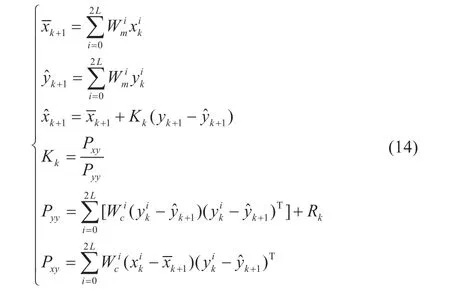
3.2 联合估计模型仿真

锂电池在使用过程中会不断老化，它的内阻会变化，容量会降低。但是辨识出来的模型参数是根据实验结果得到的定值。将SOC和SOH联合估计，根据SOH估计出来的内阻值和容量值实时修正SOC估计的参数[15]，从而提升SOC估计的精度。图8 是联合估计算法估算SOC的曲线图，图9 是联合估计算法估算SOC的误差图，联合估计算法误差在2.5%之内。图10 为不同算法估算SOC误差对比图，联合估计算法比FOMIAEKF 算法精度更高，说明联合估计算法可以有效提高SOC估算精度。表4 为不同算法估算SOC 误差对比。

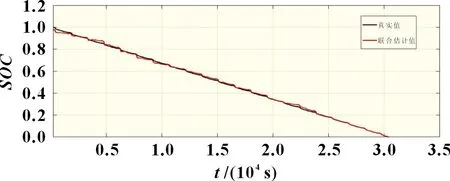
图8 联合估计算法SOC估计值

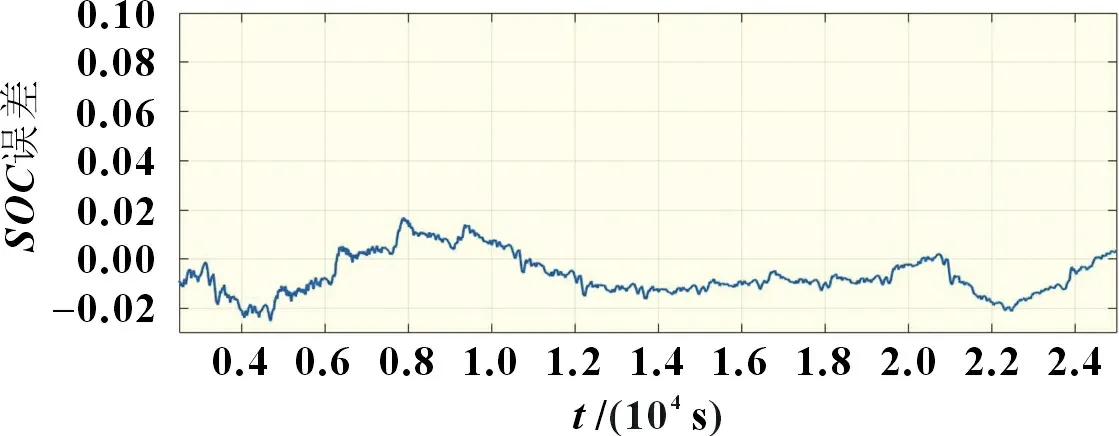
图9 联合估计算法估算SOC误差图

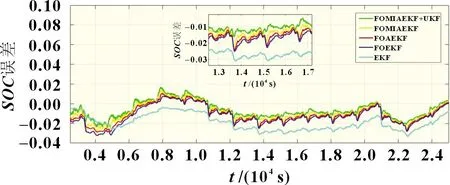
图10 不同算法估算SOC误差对比图

由表4 可知，普通EKF 算法估算SOC的平均误差为0.015 3，用分数阶理论提高模型精度后，FOEKF 算法估算平均误差为0.011 2。针对EKF 算法滤波过程中状态噪声和预测噪声恒定不变的情况，提出一种自适应EKF 算法，可以实时更新噪声方差矩阵，FOAEKF 算法估算SOC的平均误差为0.010 1，精度得到了提高，但是没有充分利用历史新息数据。针对这种情况，将单新息变为多新息矩阵，充分利用了之前未被利用的新息数据，FOMIAEKF 算法估算SOC的平均误差为0.009 1，精度相比于普通的EKF 算法有了明显提高。针对随着锂电池不断老化，模型参数会发生变化的情况，提出了联合估计算法，用UKF 算法估算SOH，实时更新分数阶模型参数，联合估计算法估算SOC的平均误差为0.007 6，精度有了进一步的提高。

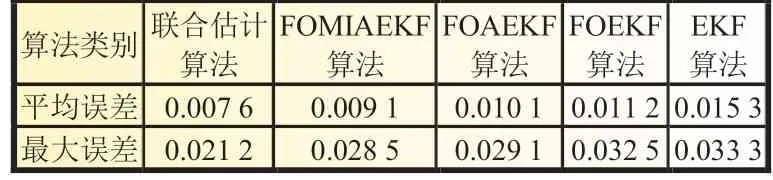
表4 不同算法估算SOC 误差对比

4 结论

本文引入分数阶思想建立锂电池等效电路模型，用AGA算法离线辨识模型参数，通过脉冲放电实验对模型精度进行验证，结果表明，分数阶的引入有效地提高了模型的精度。在UDDS 工况下，运用EKF 算法对整数阶模型和分数阶模型的SOC值进行估算，仿真结果进一步证明了分数阶模型的精度更高。随后，针对EKF 算法的不足进行改进，提出了多新息自适应EKF 算法，解决了EKF 算法噪声恒定以及未充分利用新息数据的问题，并通过与SOH联合估计实时修正分数阶模型参数，减少模型老化带来的影响。仿真结果表明，FOMIAEKF 算法和联合估计算法可以有效地提高SOC估算精度和跟踪速度。