基于分数阶多新息卡尔曼滤波法的SOC估计

宋 昊，尹丽菊，咸日常，徐明博，潘金凤

(山东理工大学电气与电子工程学院，山东淄博 255000)

锂离子电池具有循环寿命长、比能量比功率高、安全性好等优点，在电动汽车和混合动力汽车上得到了广泛应用[1]。但与传统的汽油车比，电动汽车的续航能力仍不能满足需求，所以需要电池管理系统进行能量优化，其中电池荷电状态(SOC)估计是电池管理系统的核心功能，精确的SOC估计决定了电动汽车的续驶里程[2]。

进行SOC估计的前提是对锂电池建模并获取锂电池的相关参数，常见的电池模型有等效电路模型、电化学反应机理模型及多物理场模型等[3]。电化学反应机理模型虽然精确但涉及的数学方程过多，计算太复杂，制约了其在电池管理系统中的应用。等效电路模型简单且实用价值高，常用在电池管理系统中。文献[4]建立了锂电池整数阶二阶RC 等效电路模型，并且用扩展卡尔曼滤波算法估计电池SOC，但实际上电容是分数阶的，采用分数阶更能模拟电池的极化效应。文献[5]建立了基于二阶RC 电路的分数阶锂电池模型，采用混合动力脉冲实验进行参数辨识，最后用分数阶卡尔曼滤波法进行电池SOC估计。文献[6]建立了分数阶锂电池模型，用扩展分数阶卡尔曼滤波(EFKF)方法进行电池SOC估计。但这两种方法估计出的模型精度不高，进而导致估计的荷电状态精确度不高。

本文建立了基于分数阶的二阶RC 等效电路模型，兼顾了电化学模型的精确度和等效电路模型的计算量，并采用自适应遗传算法(AGA)对模型进行参数辨识。另一方面，考虑到卡尔曼滤波估计会随时间推移造成误差积累，所以采用分数阶多新息卡尔曼滤波(FOMIEKF)进行SOC估计。通过与整数阶的扩展卡尔曼滤波估计和分数阶的扩展卡尔曼滤波对比，表明FOMIEKF 具有更高的精度，有很高的实用价值。

1 基于分数阶的二阶RC 等效电路模型建立

1.1 电池模型建立

由于动力电池从时域到频域均具有分数阶的本质，分数阶微积分在频域中建立的系统模型更加精确，所以可利用分数阶理论建立精确的电池模型[7]。本文考虑到模型既要模拟出电池电化学极化效应和浓差极化效应，还要计算简便易于应用在嵌入式系统中，在二阶RC 等效电路(图1)的基础上建立了分数阶锂电池模型。其中，UOC表示理想电压源，与SOC存在非线性关系，R0表示欧姆内阻，UT表示电池的端电压，R1和C1分别是电化学极化电阻和电容，R2和C2分别是浓差极化电阻和电容，U1、U2是两个RC 模块的电压，I表示电流，放电电流方向为正，充电电流为负。

图1 二阶RC 等效电路模型

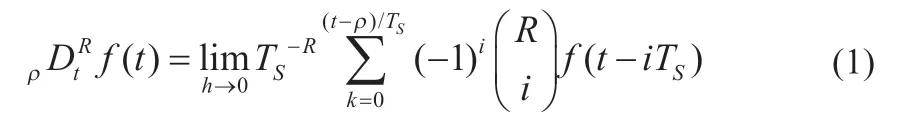
式中：ρ 和t是积分的上下限；TS表示运算步长，本文中TS取0.1 s；R表示阶次，当R为小数时表示分数阶运算；i表示运算次数，i=0,1,2,…。

图1 中两个电容可表示为：

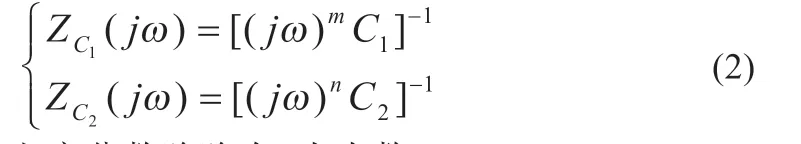
式中：m、n表示电容分数阶阶次，为小数。

根据戴维宁定理，可得出电流公式：

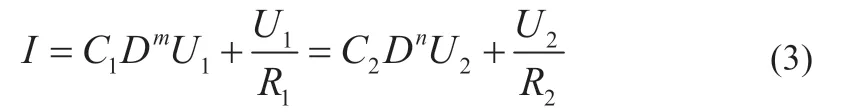
则分数阶模型状态空间方程为：

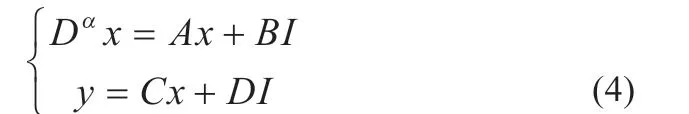
为了接下来对模型参数进行辨识和对荷电状态进行估算，必须将式(4)所示的状态空间方程离散化。根据Grünwald-Letnikov 定义，锂电池分数阶微分方程可描述为：

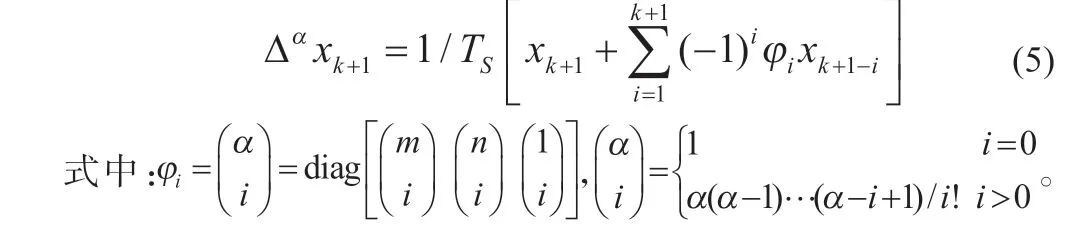
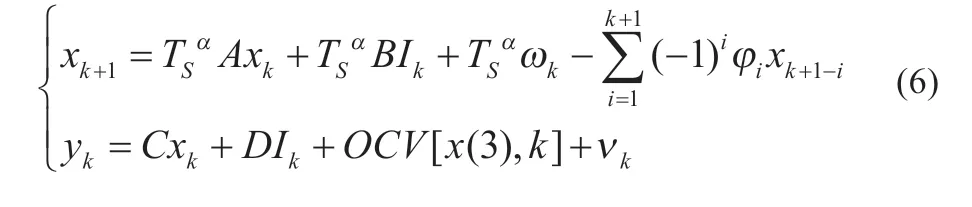
根据Grünwald-Letnikov 定义的基于二阶RC 等效电路的分数阶模型的状态空间离散系统方程和测量方程为：式中：下标k表示k时刻，用来描述当前时刻的变量，下标k+1表示k+1 时刻，用来描述下一时刻的变量；ωk表示系统噪声，υk表示观测噪声，两种噪声通常都是高斯白噪声；OCV[x(3),k]表示电池开路电压。

3.1.2 以文化变革带动内部控制创新。真正优秀的单位不是一成不变的，其内部的文化与制度都是为适应单位的发展不断变革的，同时，文化的改变可以促进内部控制的创新。以文化为基调进行内部控制的创新，这样得到的内部控制是合理的，是符合单位人员心理需求的，是不与单位控制活动相矛盾的。

1.2 自适应遗传算法参数辨识

模型框架已搭建好，但是电池的分数阶阶次等参数尚未确定，因此还需要对电池进行参数辨识。本文采用的电池放电数据是由10 节INR18650-30Q 电池并联后通过混合动力脉冲特性测试得到的。传统最小二乘法(LS 算法)参数辨识为了获取令人满意的结果，需要进行复杂的矩阵乘法，具有巨大的计算量，占用微处理器大量内存[8]；而且用于电池分数阶模型参数辨识时不能直接拟合出阶次，需要先拟合出开路电压和SOC的关系表达式，然后通过经验试凑的方法得到阶次[9]。因此，采用自适应遗传算法辨识参数，具体步骤有六步，如图2 所示。

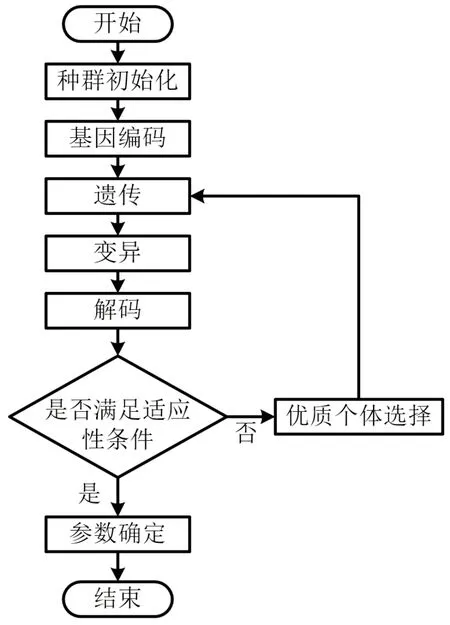
图2 自适应遗传算法参数辨识

步骤一：确定初始种群个数、交叉率、变异率，将所求参数(R1、R2、C1、C2、m、n)定义到个体基因中，随机生成初始种群基因并将其编译为二进制码。

步骤二：根据杂交概率随机挑选出父代个体和母代个体，用基因片段(部分二进制编码)交换的方法模拟种群杂交，交换后产生的新个体为子代。

步骤三：根据变异概率把部分新个体的部分基因编码取反，来模拟种群繁衍过程中后代的变异，该步骤的目的是防止结果落入局部最优解的范围。

步骤四：将杂交变异后子代的二进制基因片段解码，得到子代的数值，即模型参数辨识的结果。

步骤五：将新一代产生的参数结果代入模型中，根据实验所得电流数据求出端电压值，找出端电压误差的最大值，求出端电压误差平方和作为选择后代的基准，找到群体里中电压误差最小值及其对应位置，即最优个体。

步骤六：判断最优个体是否符合设定值或者判断繁衍次数是否超出设定代数。若符合设定条件，则结束繁衍，最优个体的参数值即为参数辨识的最终结果；若不符合，将步骤四产生的新一代进行末位淘汰，即越远离所设定条件的个体被淘汰掉的概率越高，剩下的优质个体生成新的种群，循环进行步骤二～步骤六的操作，直到出现满足条件的个体或超出设定的繁衍代数。

在自适应遗传算法中，考虑到优胜劣汰的生存法则，每一代种群中优质个体与末位个体的交叉概率和变异概率是不同的，优质个体应该有更低的交叉、变异概率以确保尽可能地被保留下来，而末位个体应该有更高的交叉、变异概率来产生新一代个体以确保能让自己的基因保留下来。根据以上分析，交叉概率CrossOverRat(i)和变异概率MutationRat(i)可以表示为：

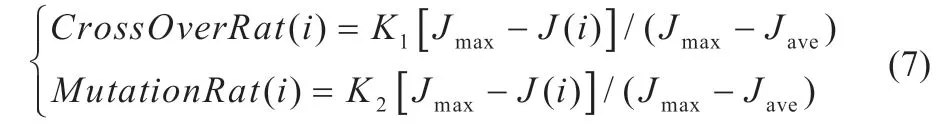
式中：J(i)反映了个体适应度；Jmax表示在种群内测量得到的输出与模型预测的输出之间差值平方和的最大值；Jave表示在种群内测量得到的输出与模型预测的输出之间差值平方和的平均值；K1、K2分别表示初始交叉概率和初始变异概率。对于适应度大的个体，其交叉概率和变异概率更接近于0。

2 分数阶多新息卡尔曼滤波SOC 估计

多新息方法是对迭代算法过程中产生的误差信息加以预测，使后验校正更加准确的一种方法。只有一个新息用来预测误差时，会导致后验测量校正信息的丢失，所以采用多个新息与卡尔曼滤波法相结合的方法，有利于提高算法的精确度。虽然采用多新息方法会使计算量增加，但考虑到估计精确度的提高更为重要，所以略微提高计算成本是可以接受的。多新息矩阵Ep,k如式(8)所示：

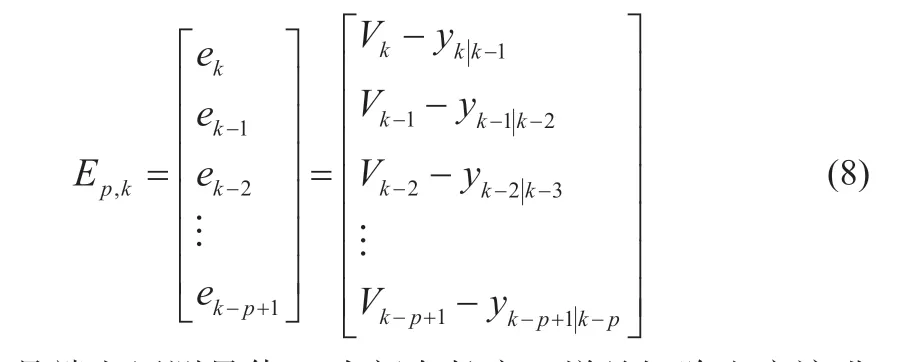
式中：Vk是端电压测量值；p为新息长度。增益矩阵也应该进行相应的扩展。

根据以上分析并结合式(4)～(6)，分数阶多新息扩展卡尔曼滤波法估计SOC公式如下：

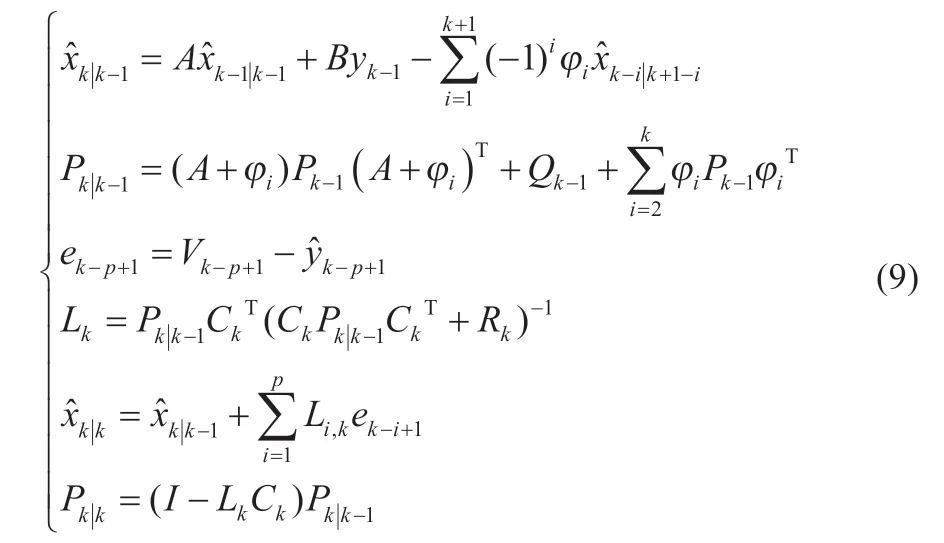
在当前状态矩阵后验估计中引入之前旧的新息作为校正项时，由于输出电压和电流中存在测量误差，旧数据造成的干扰可能会累加。除此之外，新测量值的影响应大于旧测量值的影响。若旧测量值和新测量值的不利影响均相等，也会导致干扰累加。这种情况下，将不同的权重因子λi引入不同的新息中，可以降低旧数据的校正效果。所以，k时刻状态矩阵的后验更新应改为：

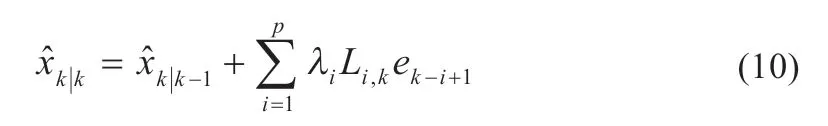
通过在不同时间的增益中加入不同的权重因子，可以权衡不同时刻的增益，实现对累积干扰的校正和抑制。不同权重如下所示：

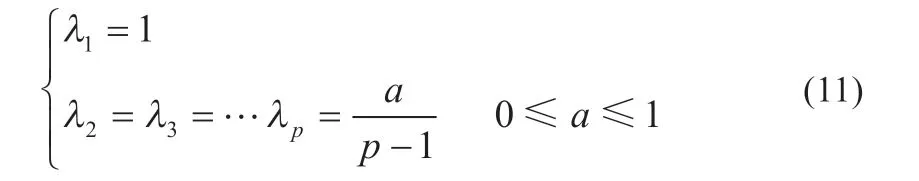
式中：λ1取值为1 是为了保证当前增益的权重最大；a为可调系数。

3 实验与仿真验证

在25 ℃室温环境中对18650-30Q 锂电池组进行混合动力脉冲测试，该电池单节的标称容量为3.0 Ah，标称电压为3.6 V，采取的放电方法是每次放电180 s，然后静置3 h，放电电流为30 A。根据最小二乘法辨识出的模型参数为：R0=0.003 7 Ω，R1=0.001 9 Ω，R2=0.003 5 Ω，C1=23 342 F，C2=501 348 F。根据自适应遗传算法辨识出的模型参数为：R0=0.003 7 Ω，R1=0.002 6 Ω，R2=0.003 2 Ω，C1=12 632 F，C2=610 476 F，m=0.989 5，n=0.983 2。将实验获得的电流数据作为模型输入，得到模型输出的端电压，将最小二乘法整数阶模型输出的端电压、AGA 分数阶模型输出的端电压与实验值进行对比，如图3 所示。与最小二乘法整数阶模型端电压相比，AGA 分数阶模型端电压与实验值更为接近。

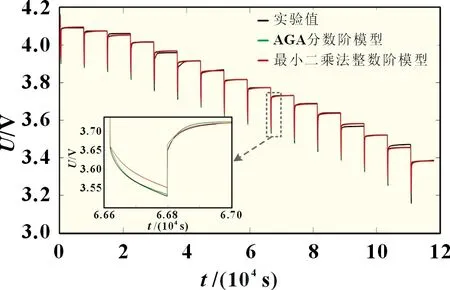
图3 模型端电压对比

为了观察更明显，将两种模型的输出电压误差进行了对比，如图4 所示。最小二乘法整数阶模型平均误差为0.005 1 V，最大误差为0.055 1 V，最大误差百分比超过1%；而AGA分数阶模型平均误差为0.004 6 V，最大误差为0.033 5 V，最大误差百分比低于1%。AGA 分数阶模型的平均误差比最小二乘法整数阶减少了0.000 5 V，最大误差减少了0.021 6 V。由此得出，AGA 分数阶模型比最小二乘法整数阶模型更能反映电池的真实情况。

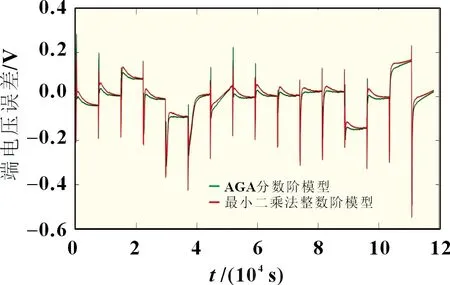
图4 模型端电压误差对比

本文的最终目的是估计电池SOC，在验证模型参数的准确性后，还需验证AGA 模型参数下SOC估计方法的精确度。首先对电池组以0.5C恒流充电至上限电压4.2 V，然后进行恒压充电至充电倍率减小到0.05C，视为电池电量充满，电池SOC=1。仍以18650-30Q 锂电池组为实验对象进行混合动力脉冲测试获得放电数据，在相同的初始条件下通过Matlab 分别使用卡尔曼滤波(EKF)、分数阶扩展卡尔曼滤波(FOEKF)和FOMIEKF 对该放电工况下的锂电池组进行SOC估计，然后与SOC参考值进行对比，结果如图5 所示。该模型参数下,三种滤波算法均可以做到有效跟踪SOC参考值，但FOMIEKF算法跟踪效果最佳。

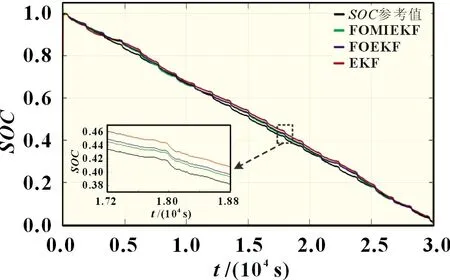
图5 三种算法估计值与SOC参考值的对比

图6 为该模型参数下三种算法SOC估计的误差，EKF 算法估计SOC的平均误差和最大误差分别为1.58%、2.86%，FOEKF 算法估计SOC的平均误差和最大误差分别为0.95%、2.01%，FOMIEKF 算法估计SOC的平均误差和最大误差分别为0.79%、1.91%。因此，本文建立的FOMIEKF 算法更能准确地估计锂电池SOC。

图6 三种算法SOC估计的误差

4 结语

本文根据锂电池的工作特性，在二阶RC 等效模型电路的基础上建立了AGA 分数阶锂电池模型，并根据此模型提出FOMIEKF 估计电池SOC的方法，通过混合动力脉冲测试和Matlab 仿真等，得出以下结论：(1)AGA 分数阶模型比最小二乘法整数阶模型更能反映电池的工作特性，其平均误差减小了0.000 5 V，最大误差减小了0.021 6 V；(2)在AGA 分数阶模型的基础上，通过FOMIEKF 算法对电池SOC进行估计，并与EKF、FOEKF 算法进行比较，得出FOMIEKF 算法估计SOC精确度更高，其平均误差不超过1%，最大误差不超过2%。因此，本文提出的锂电池模型和SOC估计方法是可行的。