锂离子电池模型参数辨识与荷电状态估算
廖根兴,赵盈盈,高雁凤,王斌锐
(1.中国计量大学工程训练中心,浙江杭州 310018;2.中国计量大学机电工程学院,浙江杭州 310018)
采用锂离子电池的巡检机器人需依据电池荷电状态(SOC)进行决策,如返回充电站自主充电、执行作业任务、休眠等待指令等,电池SOC估算是电子装置、新能源汽车等应用的电池管理系统(BMS)中防止电池过充或过放等电池安全应用的关键问题之一[1]。
SOC估算的基础是锂电池的模型与参数辨识,等效电路模型用常用的电容、电阻等元器件来描述电池的工作特性[2];二阶Thevenin 电路模型可以描述电池的极化效应及浓差效应,更好地反映锂离子电池的动静态特性[3];模型的在线参数辨识相对于离线参数辨识,考虑了电池的SOC、充放电倍率、工作电压、环境温湿度以及电池的循环次数等各种因素,可以更好地反映电池工作的实际情况。
在模型参数辨识的基础上,采用扩展卡尔曼滤波算法(EKF)将非线性系统线性化;利用KF 算法对线性系统进行最优状态估计,在初值误差较大的情况下,可以自动更新,逐渐趋近真实值。EKF 算法可较精确地估算电池的SOC,估算结果更为精确,不仅能消除安时积分法的SOC初值不确定和开路电压法无法实时在线估算电池SOC值的问题,也能避免人工神经网络(ANN)算法所需的大量实验数据[4-5]。
本文选用了锂电池的二阶Thevenin 等效电路模型,采用遗忘因子递推最小二乘法(FFRLS)算法进行参数辨识,仿真验证计算值与实测值误差在-1.3%之内,效果良好;再利用EKF 算法估算锂电池的SOC。在此基础上,开发了一套基于STM32 微控制器的软硬件系统,并进行了测试,SOC估算误差在6%之内,可应用于自行研制的地铁站台巡检机器人。
1 等效电路模型的在线参数辨识
1.1 锂离子电池等效电路模型
本文选择二阶Thevenin 等效电路作为锂离子电池模型,如图1 所示。

图1 锂电池二阶Thevenin等效电路模型
二阶Thevenin 模型电路结构由UOC(开路电压)、R0(欧姆电阻)、R1、R2、C1和C2构成。R1和C1描述电池反应中的电化学极化反应;R2和C2描述电池反应中的浓差极化反应;UL为电池的端电压;I为等效模型电路中的电流。根据基尔霍夫定律,由电路模型可得电压和电流的关系式:

1.2 锂离子电池开路电压特性实验
电池放电时,电压有迟滞性,需静置一段时间后才能达到稳定值,因此电池放电、长时间静置后所测得的电压开路电压OCV与SOC曲线标定后才可作为标准曲线。本文采用松下NCR18650B 锂离子动力电池,额定电压4.2 V,额定容量3.4 Ah,实验环境温度为25 ℃,测试方法与步骤为:(1)首先将电池恒流-恒压充电至充电上限电压4.2 V,静置1 h;(2)以0.5C放电0.2 h,即额定容量的10%,静置1 h后测试电池电压;(3)再以0.5C继续放电0.2 h,即额定容量的10%,静置1 h 后再次测试电压;(4)循环放电,当电压降至放电截止电压2.5 V 时,终止循环,静置1 h。
将SOC和测试得到的OCV电压值在Matlab 中进行多项式拟合,当阶数为6 次时,拟合效果最好,图2 为电池OCVSOC标定曲线。
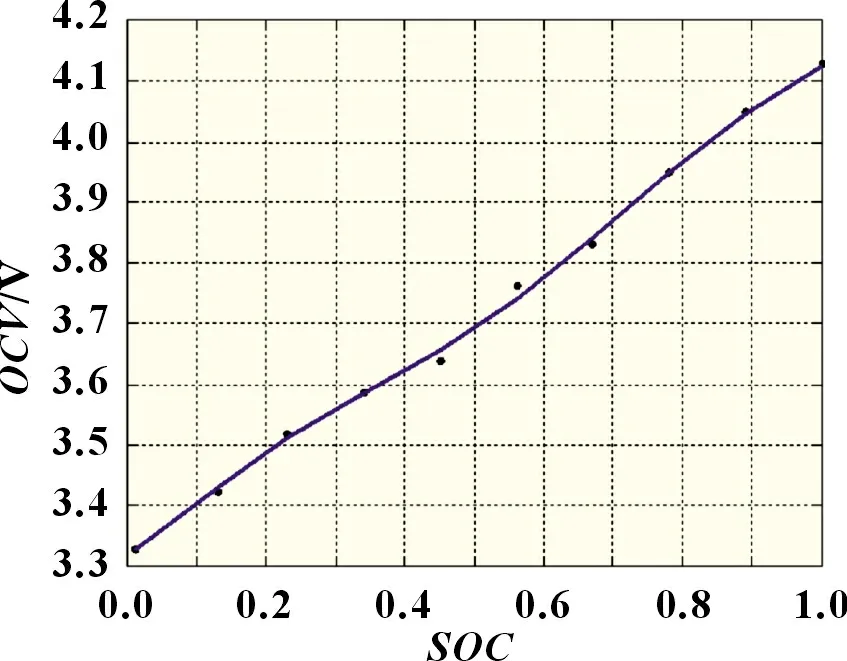
图2 OCV-SOC标定曲线
OCV和SOC的数据经6次拟合后,其数学关系表达式为:

1.3 FFRLS 算法在线参数辨识
1.3.1 等效电路的数学模型
选择FFRLS 算法对二阶Thevenin 等效电路模型进行在线参数辨识。先建立对应图1 的等效电路模型的数学模型[6],将电池视为一个单输入单输出动态系统,根据电池等效电路模型的电气关系,电流I作为系统的输入,电压U作为系统的输出,得到含有模型参数的差分方程系数,最终求得电池模型参数。
电流I为输入激励,令y=OCV-U为输出响应,对式(1)~(3)进行拉普拉斯变换及简化变换,利用s=[x(k)-x(k-1)]/T,s2=[x(k)-2x(k-1)+x(k-2)]/T2进行离散化,得到差分方程:



1.3.2 FFRLS 辨识算法
二阶Thevenin 等效电路模型的最小二乘形式为:

式中:φ(k)=[UL(k-1)-UOC(k-1),UL(k-2)-UOC(k-2),I(k),I(k-1),I(k-2)]T;θ=[k1,k2,k3,k4,k5]T。
参数辨识需确定系统采样时间和已知电池运行时的开路电压值、端电压以及电流值。在Matlab 编程环境下,参数辨识的具体流程为:(1)确定θ'(0)、P(0)的初始值大小和遗忘因子λ 的值;(2)利用安时积分法估算电池SOC(0);(3)利用OCVSOC的曲线关系,求出开路电压UOC(0);(4)载入测试数据UL(k-1)-UOC(k-1),UL(k-2)-UOC(k-2),I(k),I(k-1),I(k-2),得到φ(k);(5)通过加入FFRLS 算法得到θ=[k1,k2,k3,k4,k5]T;(6)最后通过式(5)计算电路模型中各个参数值。
2 基于EKF 算法的SOC 估算
2.1 EKF 算法估算SOC
EKF 算法根据检测获得电池的电压和电流值及FFRLS算法辨识所得等效电路参数,通过递推运算得到电池SOC最小方差估算[7-8]。EKF 算法的实质是将非线性系统线性化处理,利用泰勒公式展开后仅留下一阶项,二阶以及二阶以上的高阶项均省略,得到近似线性的系统,再利用KF 算法进行滤波迭代,最后得到最优估计值。EKF 算法非线性系统的状态方程和观测方程为:

式中:x(k)为k时刻系统的状态变量;u(k)为k时刻系统的输入变量;w(k)为k时刻系统的过程噪声;f[x(k),u(k)]为系统状态有关的非线性函数;y(k)为k时刻系统的输出变量;g[x(k),u(k)]为系统状态变量及输出变量有关的的非线性函数;v(k)为k时刻系统的观测噪声。
2.1.1 EKF 算法线性化处理
式(9)可写成式(10)类似线性系统状态方程和输出方程的形式:

2.1.2 KF 算法迭代
初始化过程,在k时刻,有:

预测过程,系统状态预测方程和系统状态协方差预测方程为:
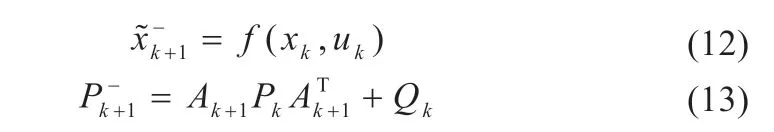
校正过程,系统反馈增益方程、系统滤波方程和系统误差协方差矩阵更新方程分别为:
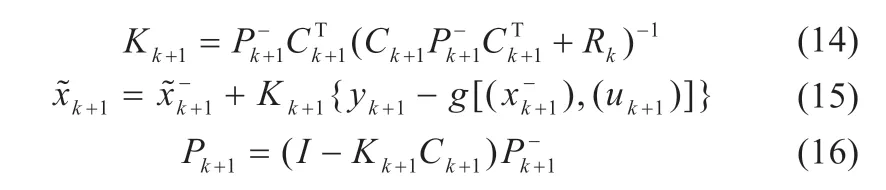
2.2 SOC 仿真结果
锂离子动力电池采用等间隔恒流放电实验,Matlab 的仿真结果如图3~4 所示。图3 为实测曲线和EKF 仿真曲线对比图。图4 为实测曲线和EKF 仿真曲线误差图。相较于电池的真实值,EKF 算法估算SOC具有较高的精度,估算误差最大为-1.3%。

图3 实测曲线和EKF仿真曲线对比图

图4 实测曲线和EKF仿真曲线误差图
3 SOC 估算系统的设计与实现
3.1 电路设计
机器人电源设计主要包括主控板设计、采集电路设计、I2C 通信和信息显示电路设计、锂离子电池组设计,图5 为机器人电源设计的主控电路板。该SOC估算系统可实现锂离子电池组单体电池电压、总电流采集,电池组六节电池的SOC估算,数据采集后上传等功能。

图5 机器人电源设计主控电路板
主控板微控制器选择ST 意法半导体公司的STM32F103C8T6,这款微控制器是基于ARM Cortex-M 内核STM32 系列的32 位微控制器。电池组电压、电流测量与采集选取TI 公司的bq76930,这是TI 公司的专用电池监控芯片,数据采集准确,稳定性高,可操作性强,寄存器设置与数据传输皆采用I2C 协议。微控制器与bq76930 通信采用I2C 协议,上位机的数据传输采用串口通信方式传输。
3.2 软件设计
系统软件设计采用Keil MDK 开发工具,完成电池电压、电流、温度各个参数值的测量以及电池组SOC数据的估算,图6 为系统的软件主程序流程图。

图6 系统主程序流程图
STM32 微控制器通过I2C 协议设置好bq76930 芯片的寄存器,每次循环时读取数据寄存器的值,转换成电压、电流值并显示。
本文SOC估算采用了EKF 算法,程序初始化时通过OCV-SOC的关系得到SOC的初始值,随着电池组的工作,通过计算可得当前时刻的SOC值,并由前一时刻的预测误差来估算当前时刻的预测误差,进而得到当前时刻的SOC最优估计值,算法子程序流程图如图7 所示。

图7 电池组SOC估算程序流程图
3.3 实验结果与分析
基于STM32微控制器的巡检机器人锂电池SOC估算系统采集电压、电流和温度数据,用EKF 算法计算并显示出SOC值,从系统读取的SOC值做为实验值;记录SOC值后关断电路,静置1 h,测量电池两端电压,根据OCV-SOC标定曲线得到SOC值作为标准值。将SOC实验值与从OCV-SOC标定曲线得到的标准值进行比较,如图8所示,两者误差不超过6%。

图8 SOC估算精度测试
4 结论
锂电池SOC估算系统能确保电池组安全可靠工作,延长电池组的使用寿命,同时可以提供数据给机器人控制系统作出最佳任务决策。本文建立了二阶Thevenin 等效电路模型并采用FFRLS 算法进行在线参数辨识。用EKF 算法对SOC进行估算,并在Matlab 软件中进行仿真,仿真结果表明EKF算法对电池组SOC估算误差最大为-1.3%。采用STM32 微控制器和bq76930 芯片完成SOC估算系统的软硬件设计并进行测试,经测试,误差不大于6%,可用于巡检机器人控制系统,下一步将研究如何改进以提高精度。

