锂离子电池组风冷性能综合传热分析

任诗皓，田嘉荣，陈捷超，方佑旭，王文豪

(东莞理工学院化学工程与能源技术学院，广东东莞 523808)

随着新能源高新技术产业的蓬勃发展，对锂离子电池的能量密度要求也越来越高，对电池组冷却方案的优化逐渐引起广泛的探讨。相关研究表明，锂离子电池的工作温度以20～45 ℃较为适宜，电池单体之间的温差应控制在5 ℃内，否则会造成电池组的局部劣化，甚至引发热失控[1-2]。锂离子电池在使用过程中应当配备相对有效的电池热管理系统，使电池的温度保持在适宜的温度范围内，而风冷散热方式因冷却介质质量小、整体结构简单、成本低、易维护且能满足电池组的散热要求等特点，是多数电池组的首选散热方式[3]。

汪等[4]采用计算流体动力学(CFD)软件对48 块圆柱锂离子动力电池组成的电池包的冷却性能进行数值模拟，分析了不同进口风速、进口风温和进口数量下电池包内部的温度分布情况。结果表明，电池模组的散热效果并非正比于进口风速，当进口风速大于3 m/s 后，电池模组的散热效果明显下降。王等[5]从电池组最高温度、最大单体电池温差、电池组标准差三个方面出发，分析了空气进出口位置、倾斜角及形状等参数对电池组散热效果的影响规律。结果表明，在进出口面积不变且进出口形状为圆形时，采用侧向通风散热方式，散热效果最佳。Chen 等[6]通过分析电池间距对散热效果的影响，发现合适的初始电池间距和调整电池间距步长，可在短时间内不影响电池性能前提下获得优化效果。Shahid 等[7]对圆柱形电池模组内温度均匀性进行数值分析，指出CFD 方法有助于捕捉空气流的死流区，对冷却方案的优化提供直观参考，并采用流动混合和增加湍流的方法提高电池模组的温度均匀性。

目前国内外的研究大多都聚焦在防止温度过高本身，较少将冷却效果和流动阻力综合起来分析电池包的散热性能。Chen 等[8]采用了流动阻力网络模型和传热模型来分析电池模组的散热方案，并获得了最佳电池间距。本文以6 块18650 型圆柱锂离子动力电池作为一个仿真单元，研究进、出风口分别为同侧和异侧时的风冷散热情况，综合考虑进口风速和进口风温对电池组散热的影响，为电池组热管理系统的优化方案提供理论参考。

1 数学物理模型

1.1 几何模型

以6 块电池作为一个仿真单元，设置了空气进出口位于同侧和异侧的两种风冷电池组模型。同侧风冷电池模组结构如图1(a)所示。电池模组模型的选取参考文献[9]的研究，即计算区域为长方体，其尺寸为145 mm×21 mm×85 mm。由6 个18650 型圆柱锂离子电池依次呈纵向排列组成，每个电池之间的间距为5 mm，各列电池单元的间距则为3 mm。空气将从电池模组左下方尺寸为21 mm×10 mm 的入口流入，气流均匀流过电池模组，带走电池表面热量，再从电池模组左上方相同大小的出口排出，完成对电池模组的风冷过程。异侧风冷电池模组结构如图1(b)所示，电池组的结构、电池的排列分布、电池间距以及空气入口位置尺寸不变，空气出口设置在电池包右上方，尺寸与入口相同。本文选用的18650 型圆柱锂离子电池的额定电压为3.60 V，额定容量为3 200 mAh，其余主要参数如表1 所示[10]。

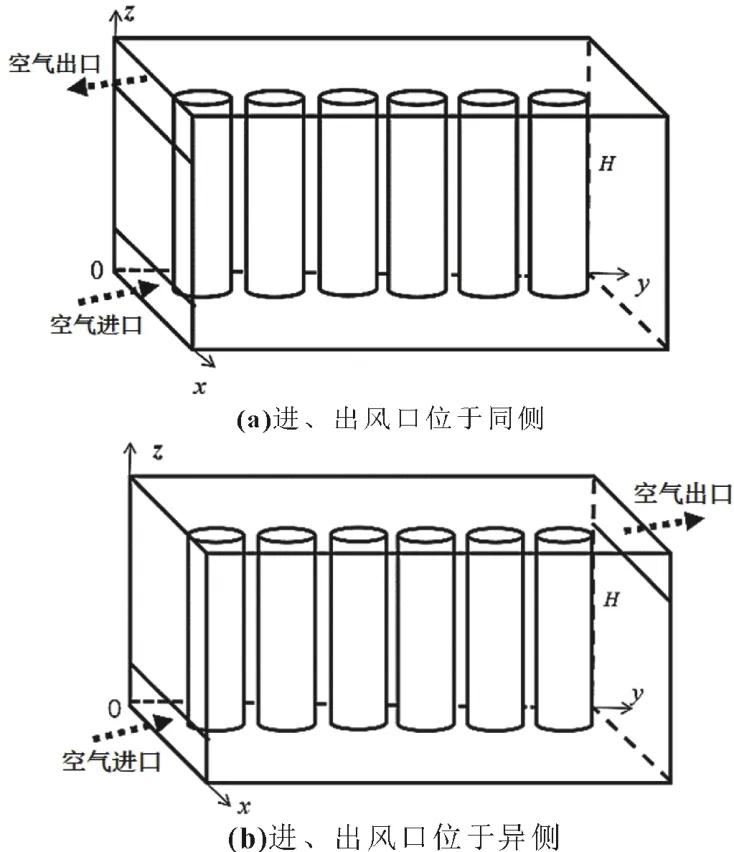
图1 风冷电池组模型示意图

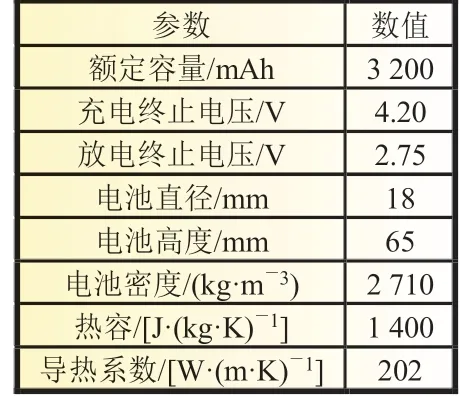
表1 电池参数

1.2 数学模型

采用k-ε湍流模型对控制方程组进行求解，为简化模型，做出以下假设：气固边界无滑移；电池物性参数假定为常数；除了动量方程中扩散项的密度值随温度变化，其它方程中的密度设为常数。因此，得到空气流动的连续性方程、动量守恒方程和能量守恒方程分别为[11]：

此外，空气导热系数h、雷诺数Re、努塞尔数Nu以及阻力系数f的关系式分别定义为：

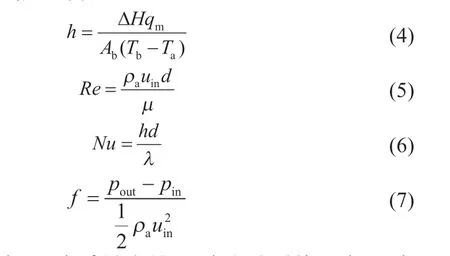
式中：ρa为空气密度；qm为质量流量；Tb为电池平均温度；Ta为空气平均温度；Ab为电池表面积；ΔH为电池组内的焓值变化；μ为空气动力粘度；uin为进口风速；λ为空气导热系数；pout为出口空气压力；pin为进口空气压力；d为进出口当量直径。

1.3 数值模拟的条件设置

基于CFD 软件对电池的风冷模型进行建模，其中，同侧风冷模型网格划分后的网格数量为666 016，异侧风冷模型网格划分后的网格数量为666 099。数值仿真设定在稳定传热条件下以2C的电流放电，环境温度为298.15 K，电池生热率为17 000 W/m3。电池模组风冷数值模拟设置进口风速区间为0.5～5 m/s，进口空气温度区间为288.15～298.15 K。将模拟电池组单元间的对称面(即平面y=0 mm，平面y=21 mm)设置为周期性边界条件，可实现以研究的单元电池组性质推广至整个电池组性质的目的。

2 结果与讨论

2.1 传热分析

电池组的最高温度随进口风速、进口风温和风冷模型的变化如图2(a)所示。同侧和异侧风冷模型中，电池组的最高温度都随着进口风速增加而降低。同侧模型进口温度为298.15 K 时、进口风速为2 m/s 时电池最高温度为308.12 K，比进口风速为1 m/s 时的最高温度318.35 K 下降了10.23 K。此外，进口风温越低，电池表面最高温度越低。同侧模型进口风速为2 m/s、进口风温为293.15 K 的电池表面最高温度为302.97 K，比进口风温为298.15 K 时的308.12 K 下降了5.15 K。可见，增加进口风速和降低进口风温在一定程度上都能增强电池组的散热能力。

进口风速、进口风温与Nu数的关系如图2(b)所示。在不同的进口风温条件下，Nu数随着进口风速的增加而增加。当进口风速为5 m/s 时，同侧风冷模型中的Nu数最高，可达8.49。在相同进口风速条件下，进口风温越低，Nu数越大，对流传热能力越强。与异侧风冷模型相比，同侧模型中Nu数随进口风速的增加速度更快：当空气进口速度为0.5 m/s 时，两种模型中Nu数相差不大；当进口风速为5 m/s 时，同侧模型中的Nu数比异侧的大2.69 倍。因此，增大风速和降低风温都能增大Nu数，从而增强空气与电池组之间的对流传热，且同侧风冷模型更有利于散热。

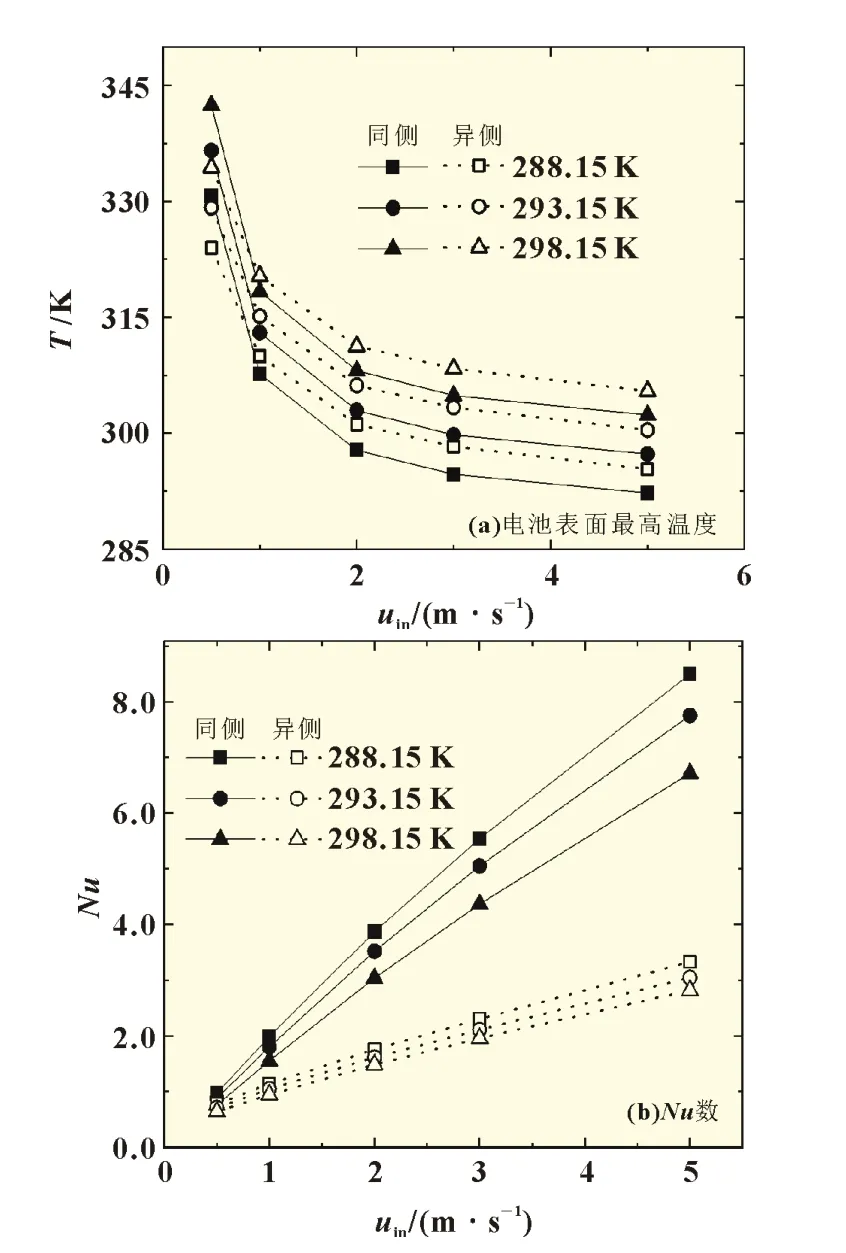
图2 电池表面最高温度和Nu数的变化曲线

图3为进口风速2 m/s、进口风温298.15 K时风冷电池模组的温度场分布图。同侧风冷模型电池表面温度维持在306 K(33 ℃)以下，同时电池单体的温差范围在5 K以内，满足电池组的散热要求。而异侧风冷模型电池表面最高温度在309 K(36 ℃)左右，这再次说明同侧风冷电池模组散热效果更佳。

图3 进口风速2 m/s、风温298.15 K 时同侧和异侧风冷模型电池表面温度云图

由图4 同侧和异侧风冷模型在截面x=72.5 mm 处的速度等值线和温度云图可知，电池单元之间的温度场分布呈对称分布，对称平面为周期边界条件所在平面(平面y=0 mm 和y=21 mm)；截面x=72.5 mm 处电池下部速度等值线呈“W”分布，即电池单元之间空气区域的流动速度比单元内部电池之间的大，因此电池单元对称面处空气区域的温度也相对较低。

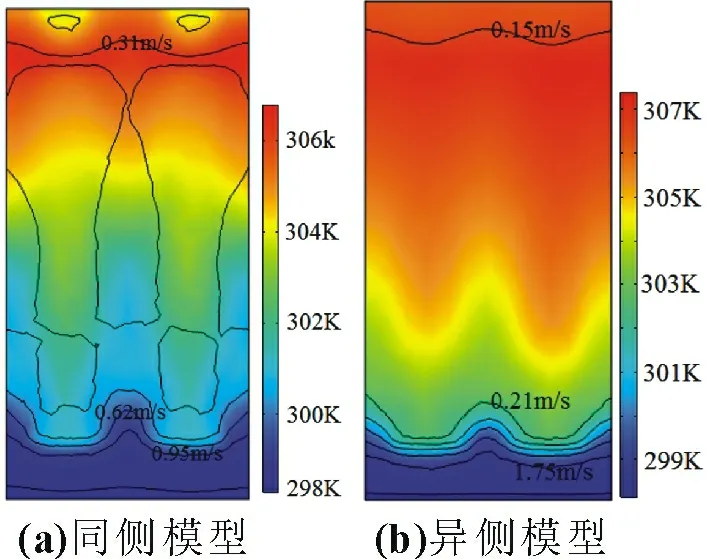
图4 进口风速2 m/s、风温298.15 K时同侧和异侧风冷模型截面x=72.5 mm处等速度线和温度云图

2.2 流动阻力分析

采用阻力系数与雷诺数的乘积(fRe)来反映流动的阻力损失情况，对不同结构类型的电池包具有普适性的参考意义。图5 为同侧和异侧风冷模型中fRe数与进口空气速度和温度的关系，在不同进口风温条件下，fRe数随着进口风速近似线性增大。风温为288.15、293.15 和298.15 K 时，同侧风冷模型fRe数的斜率分别为1 409.39、1 343.61、1 320.71，而异侧fRe数的斜率分别为1 749.21、1 667.60、1 639.30。与风速相比，进口风温对fRe数的影响相对较小；但是风速越大，进口风温对fRe数的影响也越大。当同侧风冷模型风速为5 m/s、风温为298.15 K 时，其fRe数比风温为288.15 K 时的小446.85，此差值在异侧风冷模型中为554.75。异侧模型中fRe数比同侧模型的大，由此可知，相同条件下空气在异侧风冷模型流动受到的阻力更大。

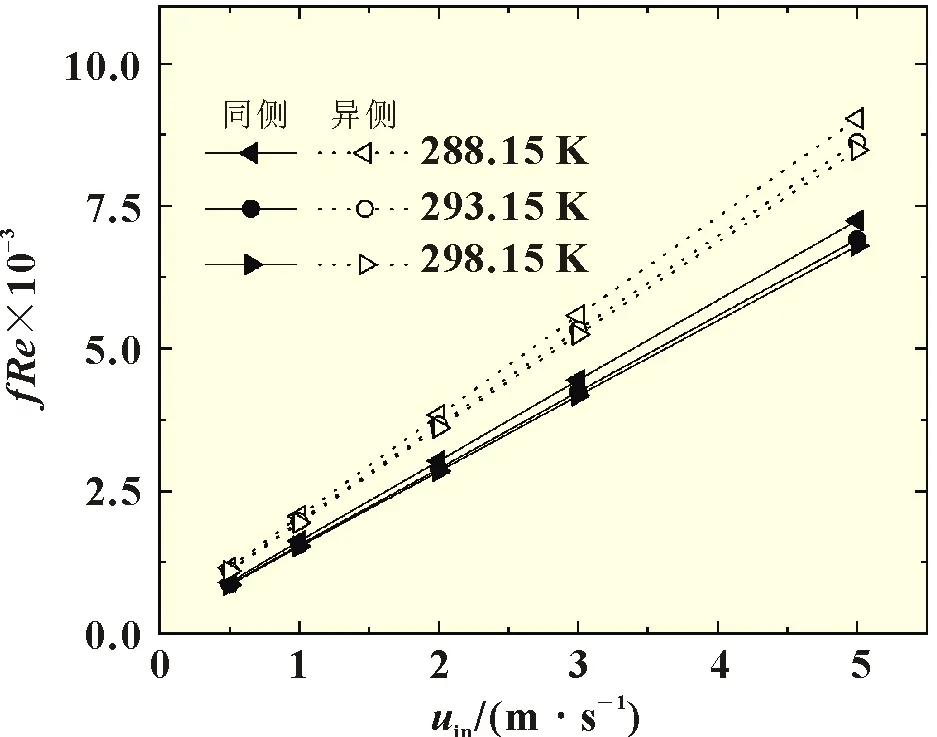
图5 风冷模型中fRe数与进口空气速度uin和温度Tin的关系

图6 为进口风速2 m/s、风温298.15 K 时同侧和异侧模型流线图，空气进口处与第一个电池之间存在一个回流漩涡，异侧模型中漩涡的流线较同侧模型的更密，显然，异侧模型中此漩涡强度更大，产生流动阻力也更大。此漩涡与Shahid等[7]通过数值模拟研究发现的死流区相类似，不利于对流传热。对异侧风冷模型而言，流动阻力的增加导致散热能力下降，换热热阻增大，从而使得异侧模型中的Nu数比同侧模型的小(图2)。此外，电池包中回流漩涡的强度随进口风速的增大而增大，并且风速足够大时电池缝隙之间也出现较强漩涡，因此，流动阻力与进口风速成正比。

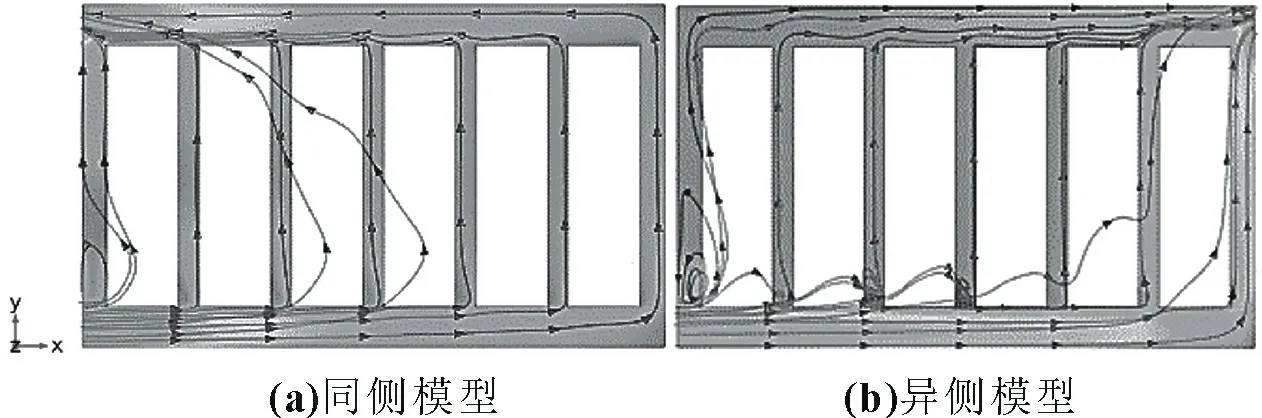
图6 进口风速为2 m/s、风温为298.15 K时同侧模型和异侧模型流线图

2.3 综合分析

众所周知，j因子和f阻力系数表征对流传热体系中传热系数和压降的参数，一般来说，随着热传递的增加，压降也会随之增加。j因子和f因子的乘积称为JF因子，以此来评价电池包内对流传热的综合效率[12]。其中，JF因子及j因子的表达式分别为：

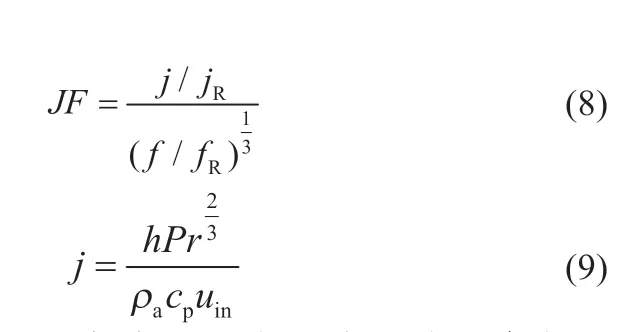
式中：Pr为普朗特数；cp为空气定压比热；下标R 表示参考工况。

JF因子随进口风速的变化如图7 所示，作为参考工况的进口空气温度为298.15 K 时，在所研究的速度范围内，JF值恒定为1。由图7(a)可知，对于同侧电池风冷模型，进口空气温度为288.15 和293.15 K 时JF值都大于1，JF值最大时的工况为进口空气速度0.5 m/s、温度288.15 K。当进口风速为0.5和1 m/s 时，进口风温越低，JF值越大；当进口风速为2 m/s 及以上时，进口空气温度为288.15 和293.15 K 的JF值相近，进口空气温度的降低对JF值的影响较小。

与同侧模型不同，异侧模型中低风速时的JF值较低，接近1，如图7(b)所示。在异侧电池风冷模型中，JF值最大时的工况为速度5 m/s、温度288.15 K。在所研究的速度范围内，JF值呈先增大后减小的趋势。因此，同侧模型中低风速的综合流动传热性能较好，而异侧模型中进口风速约为5 m/s 时综合性能相对较好，这与汪等[4]得到的结论一致。

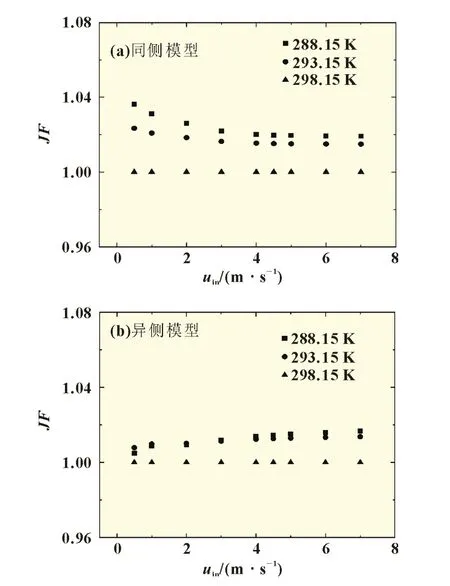
图7 同侧和异侧风冷模型中JF因子与进口风速、风温的关系图

3 结论

本文采用仿真模拟方法对于由6 个18650 型电池组成的散热模型进行研究，主要分析了进口风速、进口风温和不同风冷模型等3 种因素对电池组散热的影响，得出以下结论：对同侧、异侧风冷模型而言，增加风速都有利于增强电池组整体的散热效果，但同时增加流动阻力；降低进口空气温度有利于增加Nu数，增强电池组的散热能力；电池组同侧风冷模型中低风速工况的综合流动传热性能较好，而异侧模型中进口风速为5 m/s 时JF值最大。

致谢：感谢东莞理工学院能源与动力工程专业2018 级的余颖东和苏科宪同学。