地铁小半径曲线过渡段优化分析

孙冲

（同济大学铁道与城市轨道交通研究院，上海201804）

1 引言

铁路轨道由于对线路区段减振要求的不同，通常会设置不同的轨道刚度，对于不同的轨道刚度之间的连接，通常采用刚度变化的线路区间进行过渡，使轨道线路刚度能够平缓变化，以减缓轨道线路刚度变化带来的冲击影响[1]。近年来，随着我国城市建设的快速发展，地铁工程也得到了较快的发展，地下铁道的线路运行大多在城市市区，对线路沿线周边环境的振动与噪声控制有更高的要求，由此而带来的轨道刚度变化更为平常，曲线的过渡段设置也更普遍。

目前，针对轨道线路刚度过渡段的设置研究大多集中在线路直线区段。在直线区段上的研究中，对于钢弹簧浮置板轨，过渡段一般采用横向或者纵向加密的方式进行过渡[2]。文献[3]通过同时设置加密钢弹簧与减振扣件的方式对过渡段进行线性过渡，得出同时设置减振扣件要比单独加密钢弹簧更有效。文献[4]对于梯形轨道过渡部分采用线性改变减振垫的数量实现过渡。文献[5]探究过渡线形对过渡段产生的影响，根据动不平顺指标得出线性过渡是较为经济且有效的过渡线型。

在曲线地段，由于受到离心力的影响，车体的平稳性与曲线半径、轨道超高有很大的关系[6，7]。在曲线地段设置过渡段的工况更为复杂，本文针对曲线过渡段设置进行探索和研究。

2 模型建立及计算参数

2.1 车辆- 轨道动力学模型的建立

运用车辆-轨道耦合动力学原理建立车辆-轨道-过渡段动力学模型，利用Simpack 软件对小半径曲线线路进行仿真分析。模型总长度取180 m，直线长度为100 m，缓和曲线长度为30 m，曲线半径为300 m，仿真弹性轨道曲线长度为50 m，轨道超高120 mm，轨底坡为1/40，扣件沿轨道方向间距为0.625 m[8]。车辆采用地铁B 型车,以一节列车为研究对象,简化为具有一、二系悬挂的由车体、构架及轮对组成的多刚体系统；根据文献[1]，55 km/h 为半径300 m、曲线超高120 mm 线路的理想运行速度，因此，仿真速度定为55 km/h。

考虑本文过渡段轨下刚度设置的精确性，为便于控制，模型轨下刚度变量仅用扣件刚度代替，过渡段通过扣件刚度的变化体现。动力学模型[9]如图1 所示[K1、K2（x）、K3为各地段的轨下刚度]。

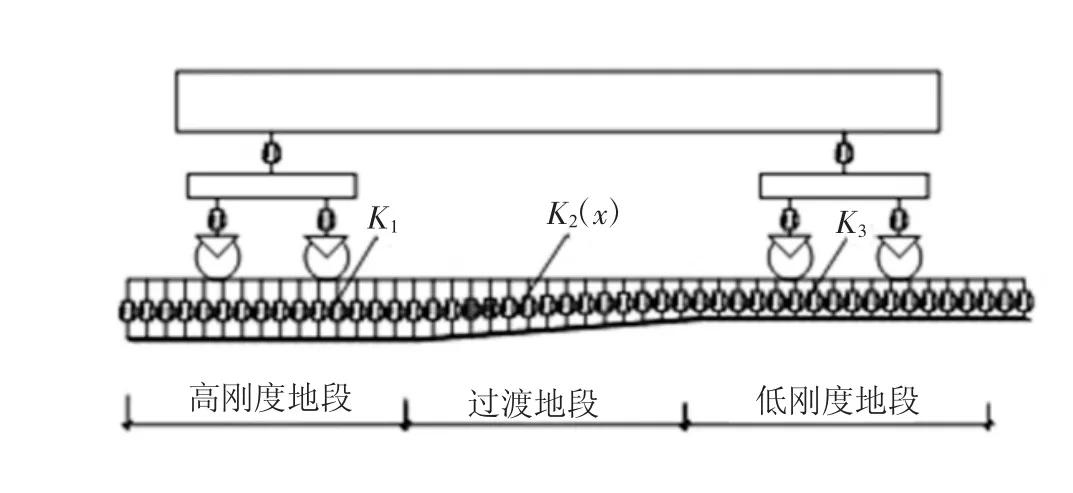
图1 车辆与过渡段轨道耦合动力学模型示意

2.2 模型计算参数

过渡段轨道结构的主要参数见表1。地铁B 型车的计算参数见表2。

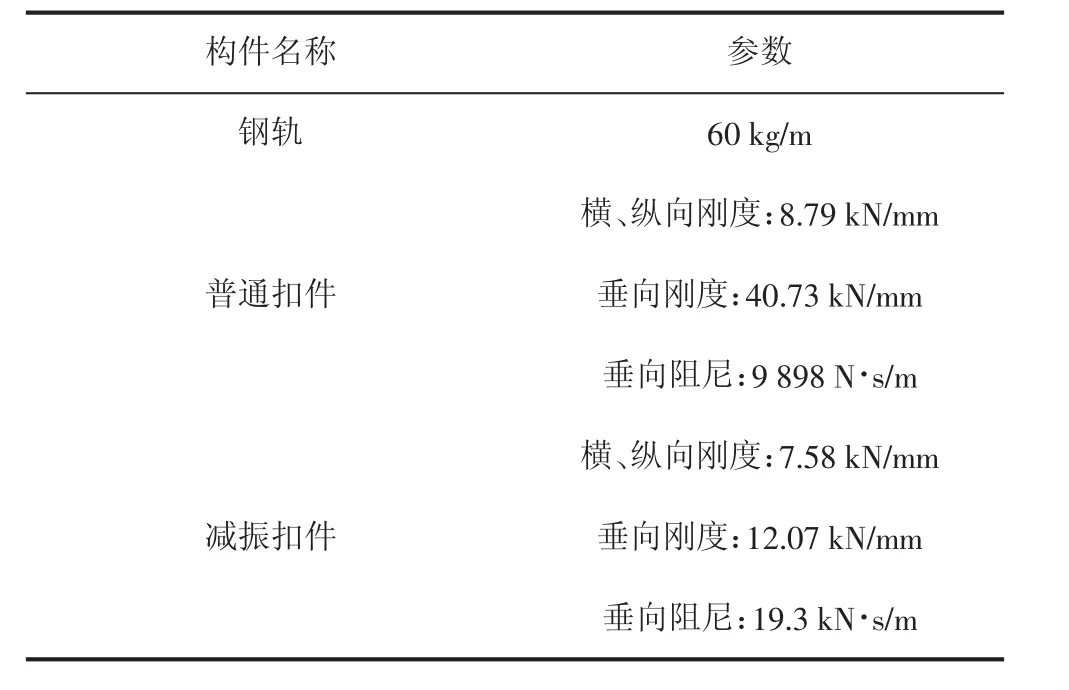
表1 有限元模型部分参数

表2 地铁B型车基本参数

3 曲线段过渡方案分析

目前，过渡段的设置形式比较单一，通常采用分段式过渡，且分段多为1 段或2 段式过渡。而曲线过渡段比直线过渡段情况更复杂，因此，需要对直线过渡方案应用在曲线上时进行分析。本节将考虑不同过渡线型、不同分段数对钢轨以及列车产生的影响。

3.1 过渡线形的影响

随着目前制造工艺、施工技术的升级，使做出各种线型的轨下过渡形式成为可能。本节探究轨下刚度线性过渡、三次抛物线过渡、余弦曲线过渡等不同过渡线型对钢轨以及车体产生的效果。过渡段设置长度多为10 m 以内，因此，本节在过渡线型比选中选定过渡段长度为6 m。

不同轨道结构的横向刚度差别不大，无须在过渡段设置横向过渡。因此，本文只设置垂向过渡，已知普通扣件垂向刚度为40.73 kN/mm，减振扣件垂向刚度为12.07 kN/mm，各种过渡形式下的轨下刚度K2（x）随过渡长度x 的变化表达式如下：

1）线性过渡

根据过渡线形表达式得出过渡段每一个扣件的刚度，计算得出不同线形过渡下内外轨的线路动不平顺曲线，如图4、图5 所示。由图4、图5 可知：线性过渡、三次抛物线过渡、余弦曲线过渡段中，由于轨下刚度为连续过渡的形式，其形成的线路动不平顺曲线是连续变化的，更加平稳，采用连续过渡曲线能够达到更好的效果。外轨产生的位移峰值为1.48 mm，内轨峰值为1.37 mm，这是由于列车速度约在55 km/h 时，列车处于欠超高状态，进而产生了偏载，使外侧钢轨受到的轮轨垂向力增加，进而使外轨产生的位移大于内轨。

图4 不同线型外侧钢轨垂向位移

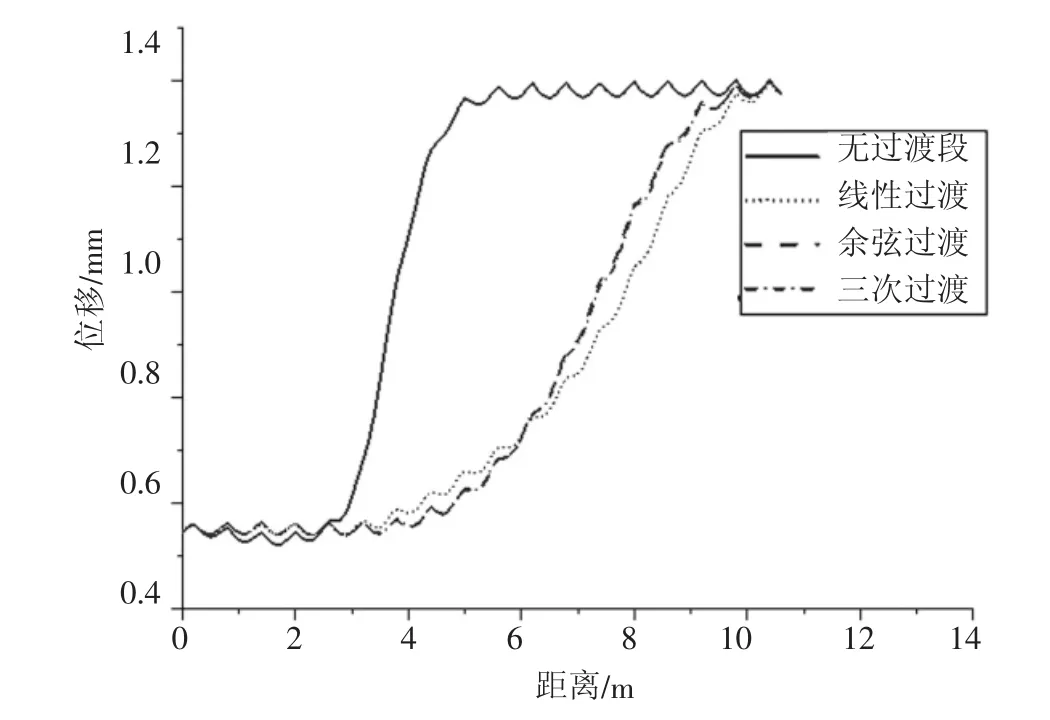
图5 不同线型内侧钢轨垂向位移

不同线形的轨下刚度过渡后，钢轨挠度变化率如图6、图7 所示。由图6、图7 可知，内外轨的变化率差异不大，在不设置过渡段的情况下，内外轨的垂向挠度变化率峰值分别为0.64 mm/m 和0.60 mm/m。其他3 种过渡线形条件下的挠度变化率均有明显的降低。其中，三次抛物线和余弦曲线线形产生的钢轨挠度变化率几乎相同，三次抛物线最大挠度变化率最大，达到0.32 mm/m 和0.31 mm/m；余弦曲线其最大挠度变化率为0.31 mm/m 和0.30 mm/m；而线性过渡的刚轨挠度变化率在线路两端较大，但在过渡段中点位置较其他连续过渡方式都小，其最大挠度变化率为0.28 mm/m 和0.27 mm/m；线形过渡的钢轨挠度变化率最大值仅为0.26 mm/m 和0.25 mm/m。

图6 不同线型外侧钢轨垂向挠度变化率

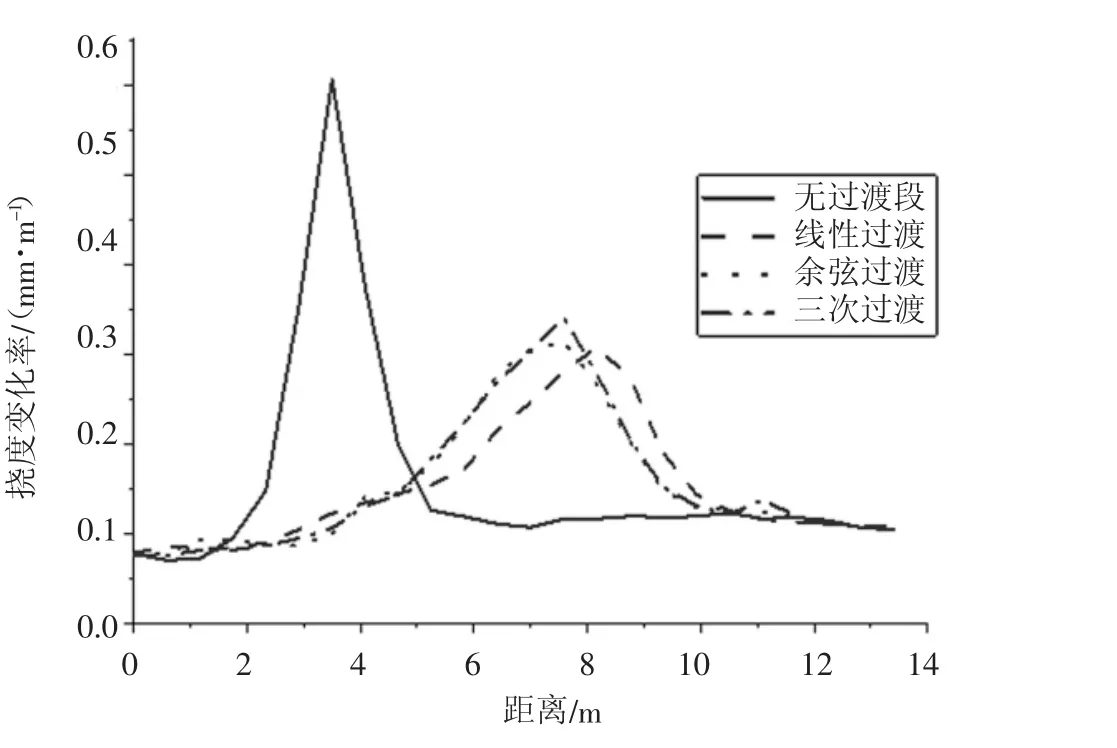
图7 不同线型内侧钢轨垂向挠度变化率

车体的垂向加速度变化情况如图8 所示。可以得出，不采用过渡、线性过渡、余弦过渡、三次过渡工况下的车体最大垂向加速度分别为0.134 m/s2、0.106 m/s2、0.112 m/s2、0.108 m/s2，采用线性过渡方案车体垂向加速度较为平稳，并且线性过渡与另外2 种过渡方案差异很小。

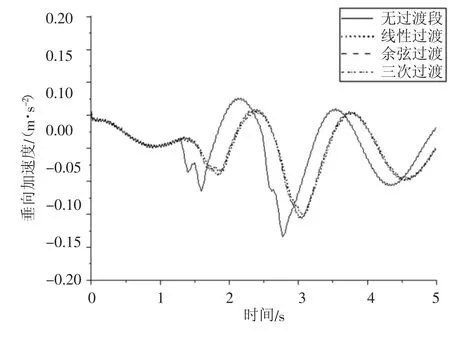
图8 不同线型车体垂向加速度

综合比较车体垂向加速度和钢轨挠度变化率以及施工便利性，采用线性过渡或者基于线性过渡的分段过渡更好。

3.2 分段数的影响

分段过渡可以将一个较大的线路不平顺差值分解为几个小的线路不平顺差值，以实现过渡效果，但施工也更困难。分段数越多，线路不平顺效果越好。根据3.1 节得出的结论，线性过渡是更为便利且有效的过渡方案，因此，本节考虑基于线性的分段过渡方案，比较无过渡、一段式过渡、二段式过渡、三段式过渡以及线性过渡产生的影响以及相互之间的差异，从而选取最优的分段过渡方式[10]。

因在55 km/h 工况下外侧的钢轨响应均大于内侧钢轨响应，故本节只展示外侧钢轨在不同分段数下的钢轨垂向挠度变化率（见图9），不采用过渡、一段式过渡、二段式过渡、三段式过渡以及线性过渡工况下的最大钢轨挠度变化率分别为0.64 mm/m、0.44 mm/m、0.35 mm/m、0.29 mm/m 和0.26 mm/m。分段数越多，钢轨最大垂向挠度变化率越小，过渡效果越好。

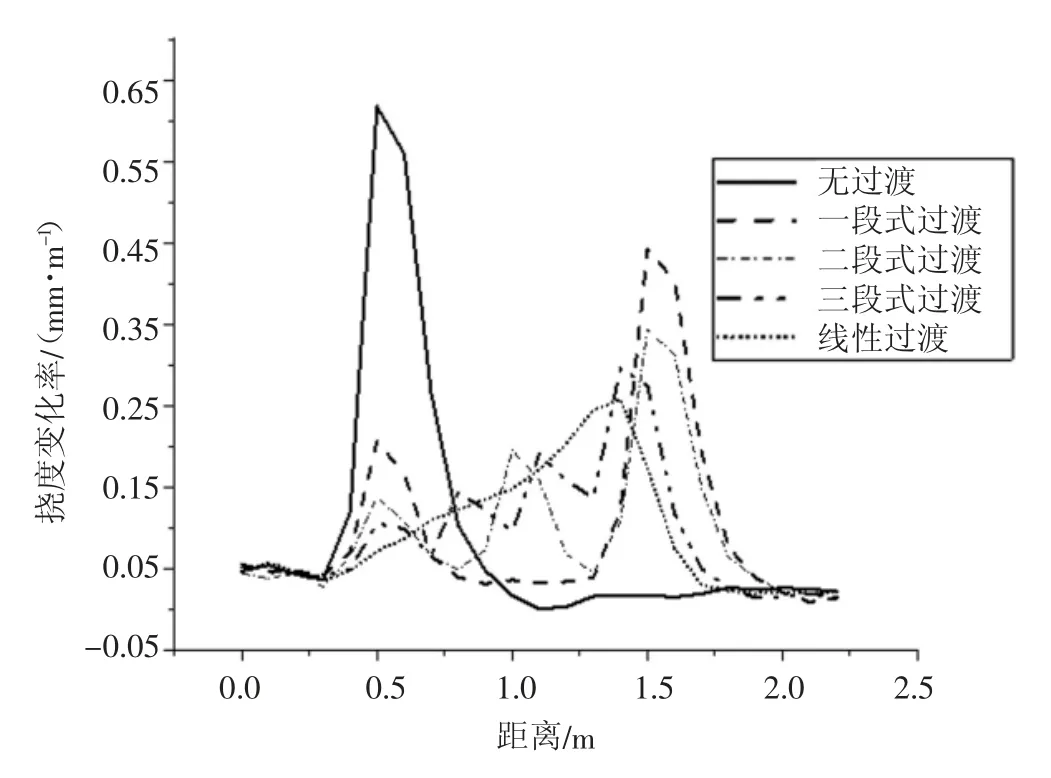
图9 不同分段数的外侧钢轨垂向挠度变化率

不同分段数的车体垂向加速度如图10 所示。由图10 可知：无过渡、一段式过渡、二段式过渡、三段式过渡以及线性方案的最大车体垂向加速度分别为0.134 m/s2、0.119 m/s2、0.114 m/s2、0.11 m/s2、0.106 m/s2。对比不设置过渡段，各个过渡方案最大车体垂向加速度分别减少11.2%、14.9%、17.9%、21%。不同分段式过渡效果差异较小，考虑到施工便利性，宜采用线性一段式过渡方案。

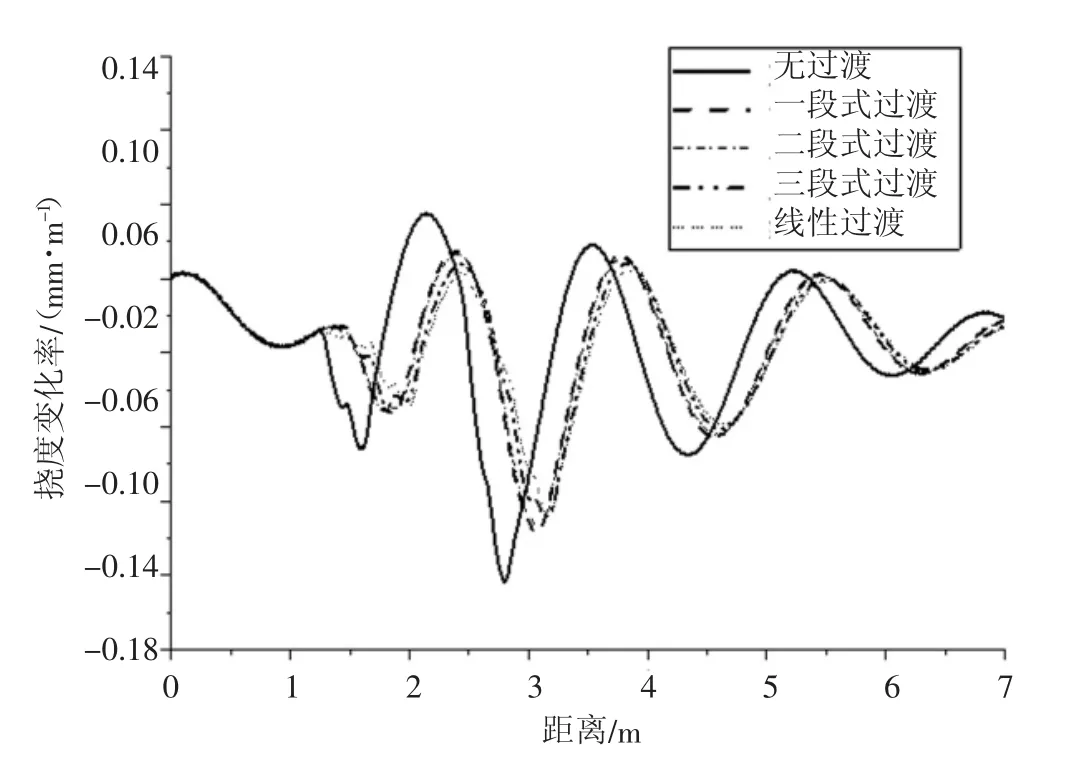
图10 不同分段数的车体垂向加速度

4 结论

针对目前地铁小曲线半径，利用多体动力学仿真软件Simpack 和有限元软件联合仿真的方法，建立地铁-轨道系统动力学模型，从轮轨间作用力以及车辆-轨道系统的振动响应角度出发，分析不同轨下刚度过渡形式下的轨道不平顺指标以及车体动力响应参数，主要得出以下结论：

1）良好的过渡段轨下刚度线形设计可明显改善线路过渡效果，分析比较线性、余弦、三次过渡线形的效果，采用线性过渡或者基于线性过渡的分段过渡更好。

2）过渡段分段数越多，过渡效果越好。综合比较不同线性分段式过渡方案对钢轨和车体产生的效果，宜采用线性一段式过渡方案。