考虑桩土相对位移的超长单桩沉降计算研究

蒋蓓，陶海冰

（1.浙江建设职业技术学院，杭州311231；2.方远建设集团股份有限公司，浙江 台州318000）

1 引言

滨海软土地区经济发达，高层、超高层建筑工程与大型基础设施工程发展迅速。因超长桩基础具有承载力高，沉降量小等优点，故在滨海软土地区得到了广泛应用。在桩基设计过程中，优化超长桩的桩长，避免因桩长过长造成浪费，是节约经济成本与保护环境的内在要求。因此，对于超长桩的有效桩长研究一直是桩基研究的热点问题。

超长桩的有效桩长计算理论主要基于荷载传递函数法[1-5]。荷载传递函数法可以基于线性或者非线性的桩侧摩阻力与位移关系来进行推导。但传统荷载传递函数法使用都是建立在桩周土体与桩身变形协调这一假设基础上的，而实际情况是桩周土体与桩身存在相对位移，变形并不协调。因此，在考虑桩周土体与桩身变形不协调时，即存在桩土相对位移的情况下，对超长桩的有效桩长计算进行探讨，是一种有意义的尝试。

2 基于传递函数法的控制方程

以单桩为研究对象，依据弹性理论，可得到单桩受竖向荷载下的基本微分方程：

式中，Ep为桩身弹性模量；Ap为桩身截面面积，Ap=πr02，r0为桩半径；U 为桩身横截面周长，U=2πr0；z 为基础埋深；wp(z)为桩身位移函数；τ(z)为桩土界面的剪应力函数。

假设桩身任意一处位移由桩土相对位移与桩周土体位移部分相加组成[6]，引起桩周土体的位移与桩土间的剪应力有关，桩土相对位移也与桩土间的剪应力有关。可得：

式中，ws(z)为桩周土体位移函数；Su(z)为桩土相对位移。

根据剪切位移法可得，土体位移与桩侧桩土间剪应力关系如下：

式中，Gs为桩周土的剪切模量；rm为单桩影响半径，此处按Cooke 建议取rm=20r0。

引入Boxlucasl 函数[7]来定义桩土相对位移与桩土摩阻力产生剪应力之间的关系，则有：

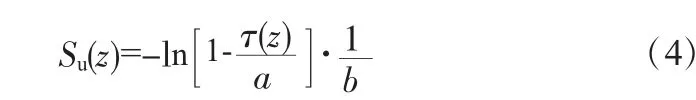
式中，a 与b 为实验参数，其物理意义参见图1[8]，图中，τult为土体极限剪应力。

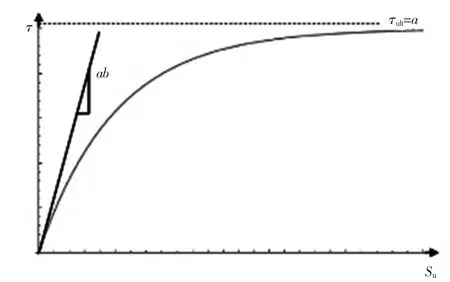
图1 桩土间剪应力与桩土相对位移对应的Boxl ucasl函数关系示意图

3 边界条件确定

根据有效桩长的定义，超过有效桩长的桩身不提供侧摩阻力，桩顶部轴向荷载全部由有效桩长以上部分的桩侧摩阻力来承担，不考虑桩端阻力[8]。

那么反过来推导，如果当前桩身长度为有效桩长，当桩顶竖向位移达到容许沉降量时，其所承受桩顶荷载必然是设计时最大荷载。即，在已知边界条件wp(0)=wp0，桩端阻力P(L)=0的情况下，求解微分方程，然后再求解桩顶荷载Pu（其中，wp0为桩顶控制沉降，P 为桩身反力）。

当桩基埋深z=0 时，将式（2）～式（4）与wp(0)=wp0联立，可得桩顶初始剪应力：

4 控制方程数值求解与算例分析

所得控制方程为二阶非线性常微分方程，第三类边值条件，无法得到其解析解，可以应用有限差分法进行数值求解。

取Ep=30×109Pa，Gs=5×106Pa，r0=0.25 m，rm=20r0，a=7.5×104Pa，b=7.5×102m-1，桩顶容许沉降量为wp0=0.040 m。

当有效桩长为L=80 m 时，可计算得到桩身位移、桩周土体位移与桩土相对位移沿桩长关系如图2 所示。

图2 桩身位移、桩周土体位移与桩土相对位移沿桩身分布

从图2 可以看出，桩土相对位移在桩身前端变化剧烈，而土体位移在桩身前半段变化不明显。桩周土体位移在桩身后端开始出现下降，而桩土相对位移在桩身后半段缓慢下降趋于零，其变化率明显小于桩周土体位移变化率。因为在此处假设剪应力与桩周土体位移与桩土相对位移都是正相关的，那么可以看出，在桩身的后半段，桩周土体的位移对剪应力发展起主要作用；而在桩身前半段，桩土相对位移对剪应力发展起主要作用。

为了验证本文采用数值计算的可靠性，将计算结果与采用剪切位移法考虑桩土变形协调的传递函数法计算结果进行比较，采用该方法得到的桩顶荷载与有限桩长的关系为：

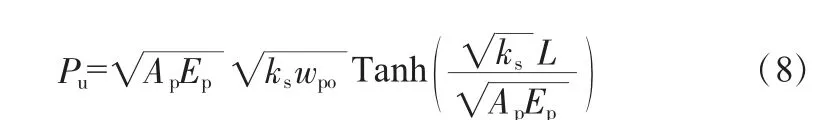
式中，ks为计算模型切向的切线模量。这里为了表述方便，将采用剪切位移法考虑土体与桩体变形协调得到的解析解称为“桩土变形协调解析解”（以下简称“解1”），将考虑桩土相对位移的传递函数法得到的数值解称为“桩土存在相对位移数值解”（以下简称“解2”）。根据上述的计算参数，得到2 种解下桩顶荷载与有效桩长的关系曲线，如图3 所示。

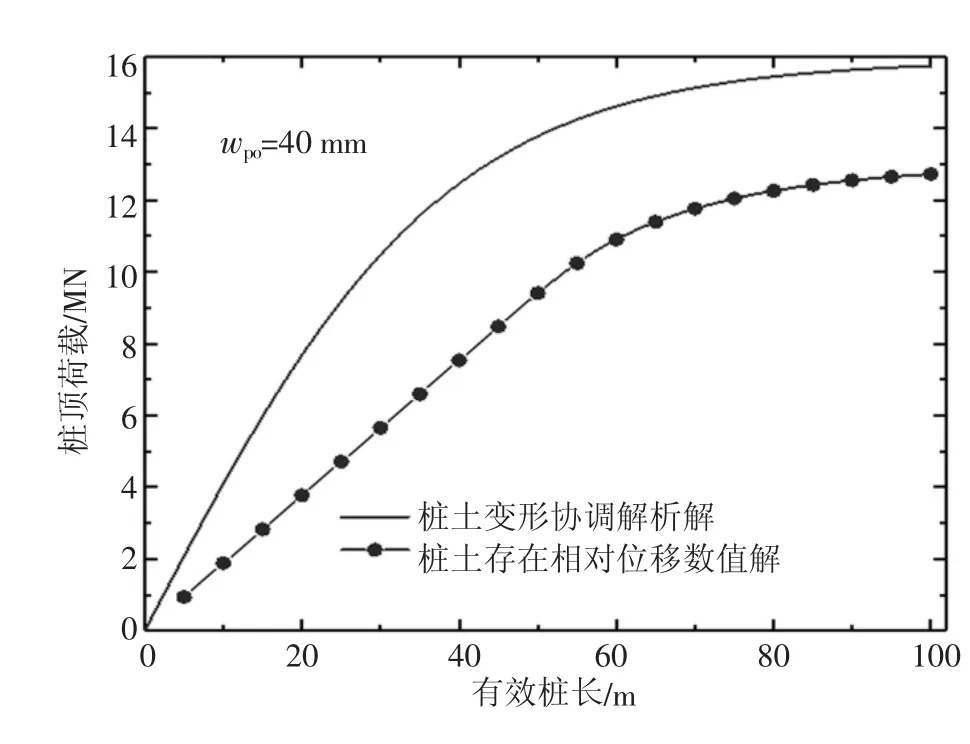
图3 解1 与解2 有效桩长与桩顶荷载关系曲线对比

从图3 可以看出，无论哪种解，桩顶荷载随有效桩长的增大而增大，但增大的趋势都随着有效桩长增大而减小，都有趋于某一值的趋势，已有文献报道过这种现象[10，11]。2 种方法所得曲线的形式与发展变化大致相同，间接说明了采用解2 的可靠性。在有效桩长相同时，解2 所得的桩顶荷载要小于解1所得到的桩顶荷载，并且解2 曲线中桩顶荷载随有效桩长增长趋势也比解1 曲线增长趋势要缓慢。

采用解2，当保持参数b 不变时，相同的有效桩长对应的桩顶荷载随着参数a 增大而增大。并且桩顶荷载随有效桩长增长趋势随着a 值减少而变缓，如图4 所示。

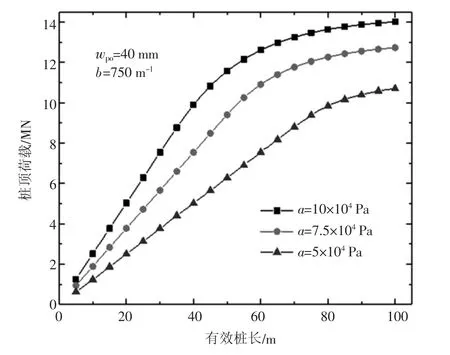
图4 参数b 不变，参数a 变化时有效桩长与桩顶荷载关系曲线对比

当参数a 保持不变时，参数b 变化时，有效桩长与桩顶荷载关系曲线对比如图5 所示。当有效桩长相同时，桩顶荷载随着b 值增大而增大。桩顶荷载随着有效桩长增长趋势随着b值增大而变陡，但当b 值增大到一定程度后，不同b 值对应曲线趋于重合。

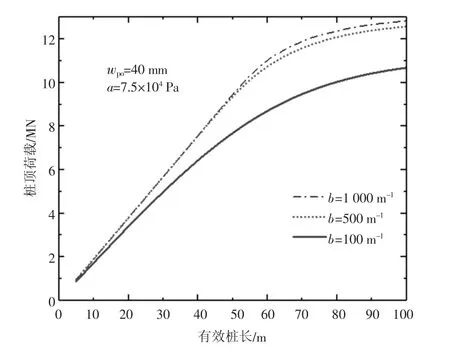
图5 参数a 不变，参数b 变化时有效桩长与桩顶荷载关系曲线对比

5 结论

1）考虑桩土相对位移的传递函数法来进行超长桩有效桩长计算理论的研究，比基于桩土变形协调的传统传递函数方法要更符合桩土共同作用下的实际物理模型。从计算结果来看，相对位移从桩顶向桩底变小，桩土相对位移对桩土间剪应力发展的影响主要体现在靠近桩顶的桩身段。

2）在相同有效桩长情况下，桩顶沉降量相同时，采用解2得到桩顶荷载要小于用“桩土变形协调解析解”得到的桩顶荷载。

3）相对位移与剪应力函数关系采用Boxlucasl 函数时，在桩顶沉降量相同情况下，参数a 值与参数b 值越大，相同有效桩长对应的桩顶荷载值也越大。桩顶荷载对应有效桩长的变化率也越陡，但参数b 增大到达一定值后，由参数b 引起的变化就越来越不明显。