CGRaBS J2345-1555 多波段流量相关性及射电波段多普勒因子估计*

张欢 张皓晶 陆林 马凯旋

(云南师范大学物理与电子信息学院,昆明 650500)

收集了Fermi/LAT,Catalina,OVRO 发布的CGRaBS J2345-1555 长期射电(15 GHz)、伽马、光学V 波段的流量和星等数据,用离散相关函数方法评估了多波段间的相关性,结果显示伽马波段和射电波段的相关系数为0.53,时间延迟约为90 天,伽马波段比射电波段超前约90 天;射电和光学V 波段的相关系数为0.84,时间延迟约为—300 天,光学V 波段比射电波段超前约300 天;伽马和光学V 波段没得出具体相关性.说明光学波段由同步辐射主导,射电波段与光学波段的时间延迟可以解释为光学波段的辐射区域在上游,射电波段在下游.而伽马波段与射电波段是同源的.用亮温度方法计算了该天体射电波段的多普勒因子,多普勒因子平均值为12.25,并随光变曲线振荡.分析得出喷流具有明显聚束效应.射电波段辐射流量变化来自于喷流.

1 引言

耀变体(Blazar)的辐射以相对论聚束的喷流为主,喷流与观测者视线方向夹角很小[1],其核主导的相对论聚束喷流有快速、大幅光变以及视超光速运动的特点.耀变体的光变可以在短时间内增加几个数量级,变化的时间范围从几天到几个月不等,并且在各个波段都能观测到其变化,同时还伴随着剧烈的偏振变化.耀变体分为两种次型,一为蝎虎天体(BL Lac),另一类为平谱射电类星体(FSRQ).耀变体能谱显示出两个明显的峰值,低能峰解释为由同步加速辐射产生,高能峰一般解释为逆康普顿散射产生[2].高能峰可以用轻子模型或强子模型解释[3],轻子模型又分为同步加速自康普顿(SSC)模型和外康普顿模型[2,4,5],强子模型分为质子同步辐射和质子引发的级联模型[6].目前为止,对耀变体主要的辐射机制还没有达成共识.研究多波段的相关性可以用来研究耀变体的辐射机制,还可以确定其辐射区域.Fuhrmann 等[7]研究了54 个耀变体伽马波段和射电波段(亚毫米到厘米)的相关性,结果显示这些天体的相关性具有普遍性.Cohen 等[8]研究了40 个耀变体光学波段和伽马波段的相关性,其中只有8 个源相关性超过90%.Zhang 等[9]研究了70 个费米耀变体射电和光学波段的相关性,其中有50 个源相关性很好.

CGRaBS J2345-1555 是一个典型的平谱射电类星体[10,11].其在Parkes-MIT-NARO (PMN)4850 MHz 热带观测项目中首次发现.它的位置在第4 次VLBA 校准中确定,赤经为23∶45∶12.4,赤纬为—15∶55∶08 (J2000).该天体是射电噪天体,红移为0.621.这个天体在各个波段上都有剧烈变化,早至2010 年1 月,Fermi 大视场望远镜就观测到其伽马波段有剧烈闪耀.2010 年10 月,Jiang 等[12]观测到在光学波段、近红外波段、X 射线波段和伽马射线波段观测到准同时爆发.在2013 年Ghisellini 等[13]也观测到红外、紫外和伽马射线波段的准同时爆发.

本文第2 部分将对CGRaBS J2345-1555 的射电、伽马、光学V 波段的光变数据进行数据收集并分析,第3 部分对收集对应波段的光变数据进行了相关性分析,分析得到射电、伽马、光学V 波段的辐射机制符合SSC 模型.与文献[7,9]相比,本文对射电波段进行了多普勒因子估计,并用喷流进动模型解释了多普勒因子随时间的变化,这些内容安排在本文研究的第4 部分,最后结论部分简单探讨了CGRaBS J2345-1555 射电波段流量变化来源于喷流等问题并给出简要结论.

2 数据分析

2.1 收集数据

本文收集了射电波段、光学波段和伽马波段的历史光变数据.其中射电波段来自于欧文斯谷(OVRO) 40 m 射电望远镜.光学波段来自于卡特琳娜(Catalina)光学望远镜,伽马射线波段来自于Fermi/LAT 大视场巡天望远镜.为了排除所收集数据的望远镜观测仪器误差,提高数据分析的有效精度,本文并未收集其他望远镜的观测数据,收集有效数据点共1090 个,其中射电波段679 个,光学波段280 个,伽马波段131 个.

2.2 欧文斯谷天文台(OVRO) 40 m 射电望远镜

OVRO 40 m 望远镜工作在13—18 GHz 频段,分辨率为3 弧秒,观测误差约为4 mJy (典型值为3%)[14].为支持Fermi/LAT 伽马射线太空望远镜,自2007 年以来,该望远镜进行了大规模、快速的15 GHz 观测活动,观测目标约7000 个.图1 是我们从OVRO 40 m 射电望远镜(https://sites.astro.caltech.edu/ovroblazars/)观测项目中收集的CGRaBS J2345-1555 长期15 GHz 数据.光变曲线中有8 个明显的大爆发,分别在图1 中编号为3,4,5,7,8,9,10 和12 的矩形内.5 个明显小爆发,分别在图1 中编号为0,1,2,6 和11 的矩形内.

图1 从2008 年1 月5 日至2020 年7 月1 日射电波段15 GHz 流量数据,红色矩形内为大爆发,绿色矩形内为小爆发Fig.1.15 GHz radio frequency data from January 5,2008 to July 1,2020.Strong bursts are inside the red rectangles,weak bursts are inside the green rectangles.

2.3 费米太空望远镜(Fermi/LAT)

Fermi/LAT 是1 个大面积巡天望远镜,可每3 h 扫描整个天空.LAT 可观测20 MeV 至1 TeV以上的伽马射线.CGRaBS J2345-1555 数据具有高统计意义,我们从费米科学支持中心(https://fermi.gsfc.nasa.gov/ssc/data/access)得到目标源的长期费米数据(3FGL),共131 个数据点.为方便观察伽马波段与15 GHz、光学V 波段的相关性,图2给出了伽马波段向左移动90 天后的光变曲线,可以看出伽马波段与光学V 波段具有较好相关性,与15 GHz 相关性较差.

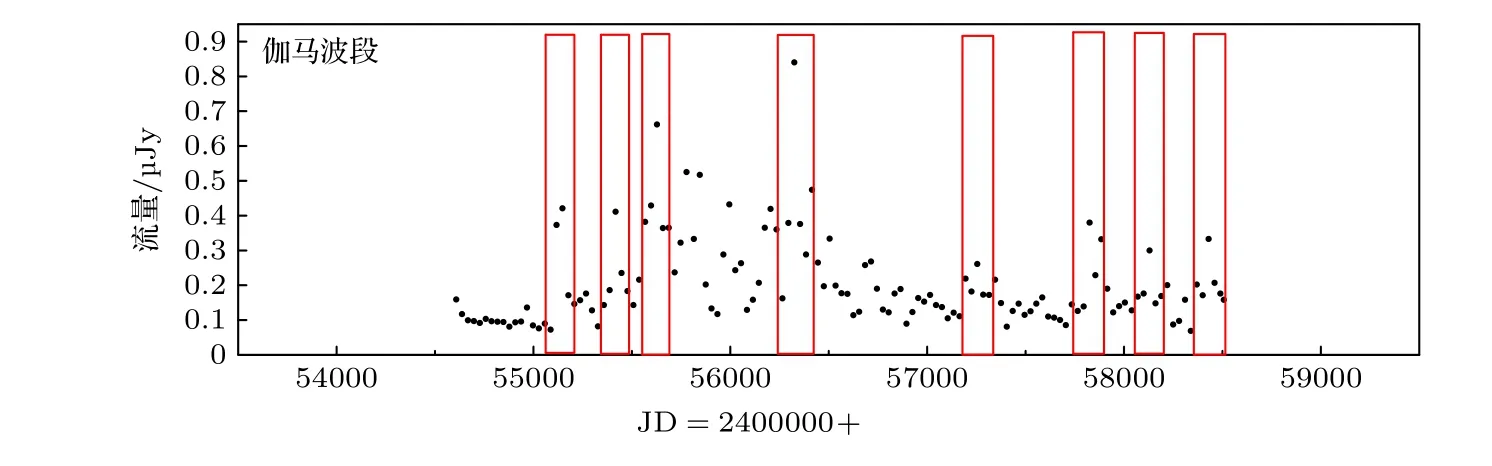
图2 从2008 年8 月19 日至2019 年4 月24 日伽马波段流量数据,红色矩形内为爆发Fig.2.Gamma band data from August 19,2008 to April 24,2019.Bursts are inside the red rectangles.

2.4 卡特琳娜光学望远镜(Catalina)

Catalina 的测光原理是孔径测光,由于孔径测光在光源混杂时不准确,因此除银河平面附近,对大量星的V 波段进行了校准.图3 是通过J2000d坐标在CRST 网站(http://nesssi.cacr.caltech.edu/DataRelease/)上得到的CGRaBS J2345-1555 的长期光学V 波段数据.为方便观察光学V 波段与15 GHz、伽马波段的相关性,给出了光学V 波段向左移动300 天后的光变曲线.容易看出在JD=2455500 之前V 波段相对平坦,有几个微弱的爆发,但在JD=2455500 之后有两个大的爆发和两个小爆发,与射电波段的爆发时间很接近.

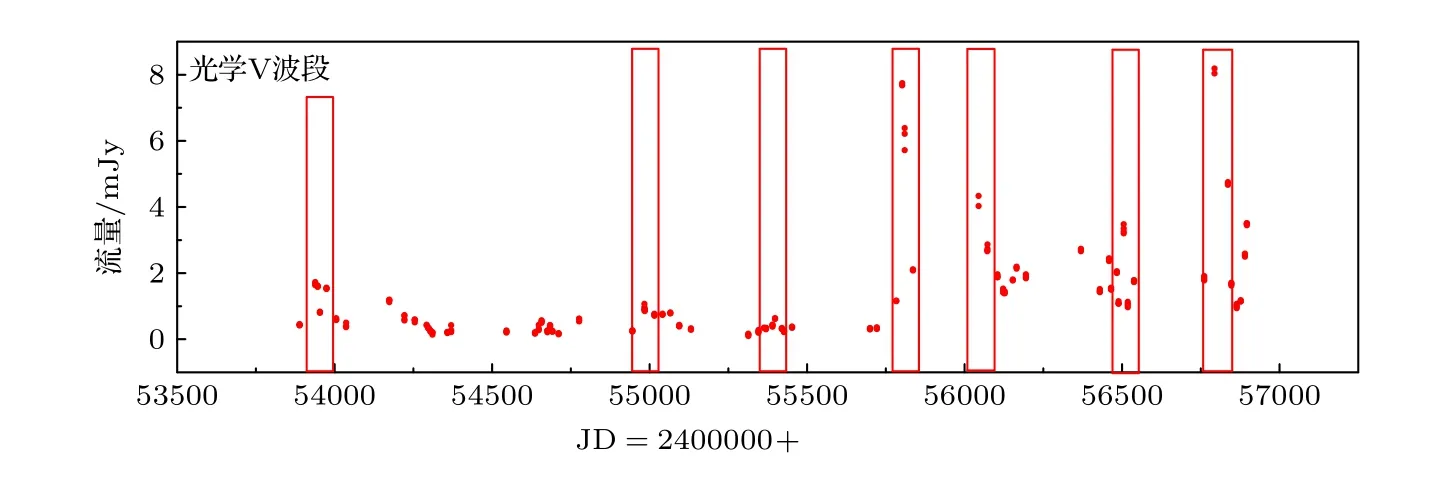
图3 从2005 年11 月30 日至2010 年8 月13 日光学V 波段流量数据Fig.3.Optical V-band data from November 30,2005 to August 13,2010.Bursts are inside the red rectangles.

3 相关性分析

这里利用Edelson 和Krolik[15]的离散相关函数方法来分析两个波段之间的相关性和时间延迟,这种方法即使在光变曲线不均匀的情况下,也能很好地计算相关性.对于两个不同波段数据列ai和bj,任意数据对 (ai,bj) 有

均后可得到

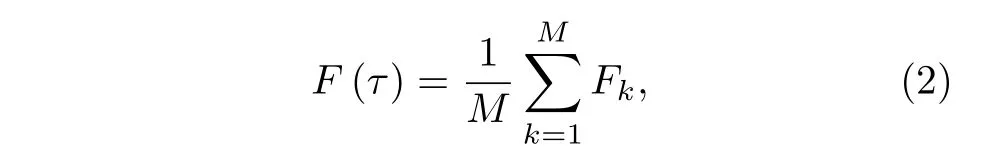
标准偏差为

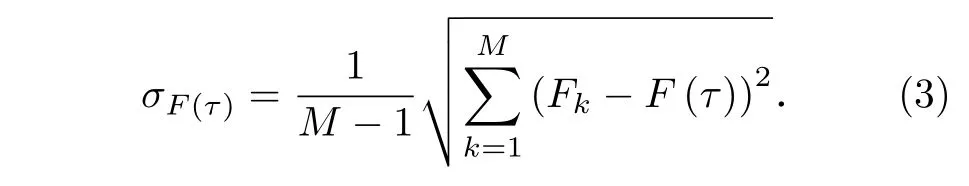
对CGRaBS J2345-1555 的射电、伽马射线、光学V 波段两两之间进行互相关分析,射电、伽马、光学V 波段光变曲线如图1—3 所示,相关性计算结果如图4—6 所示.通过局部归一化,离散相关函数中的点被限制在—1 到1 之间,每个点都直接表示每个滞后的线性相关系数[16].图4 是伽马波段和射电波段离散相关函数计算结果,峰值在(90,0.53),超过99.7%置信曲线.对相关系数的峰进行高斯拟合,得到的时间延迟约为106 天,相关系数为0.484,时间延迟为正值表示伽马波段领先射电波段,与Fuhrmann 等[7]研究的54 个源的结果相似.图5 是射电波段和光学V 波段离散相关函数的计算结果,峰值在(—300,0.84),超过99.9%置信曲线.对峰值进行高斯拟合,拟合得到的时间延迟约为—310 天,相关系数为0.720,负值表明射电波段落后于光学V 波段310 天,与Zhang等[9]的估计相似.图6 为伽马波段和光学V 波段离散相关函数计算结果,可见离散相关函数分布弥散,在—500—500 天之间没有明显的峰值存在,说明伽马和光学V 波段之间不存在具体相关性.

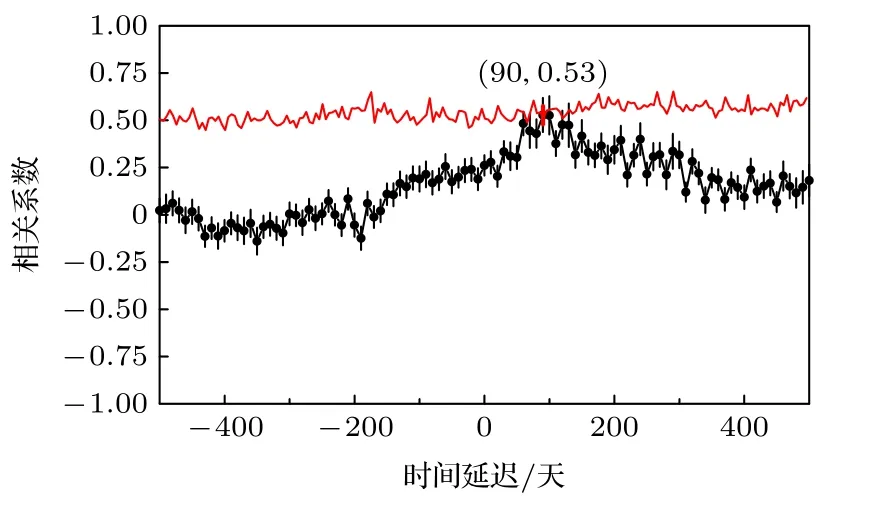
图4 红色曲线为99.7%置信曲线,黑色点为伽马和射电15 GHz 波段离散相关函数的计算结果Fig.4.Red curve is the 99.7% confidence curve,and the black points are the calculation results of the discrete correlation function of the gamma band and the radio 15 GHz band.

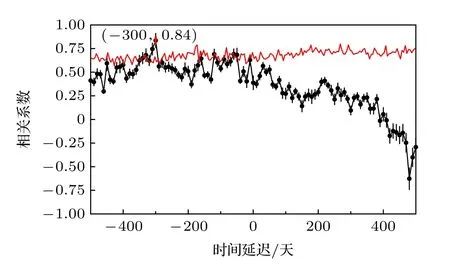
图5 红色曲线为99.9%置信曲线,黑色点为射电波段和光学V 波段离散相关函数计算结果Fig.5.Red curve is the 99.9% confidence curve,and the black points are the calculation results of the discrete correlation function of the radio band and the optical V band.

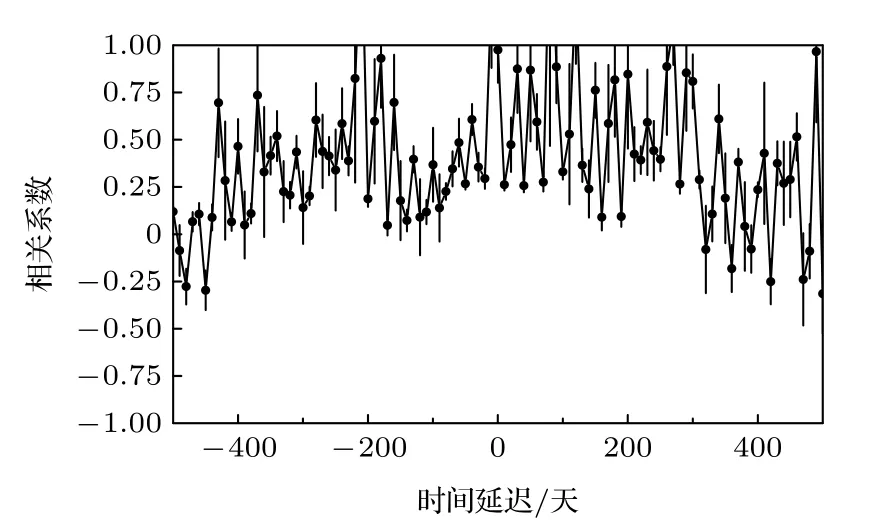
图6 伽马波段和光学V 波段离散相关函数计算结果Fig.6.Calculation results of the discrete correlation function of the gamma band and the optical V band.

4 射电波段多普勒因子估计

耀变体喷流具有视超光速和喷流与视线方向夹角小的特点,但视超光速的大小和喷流与视线方向夹角很难测量,本文中使用亮温度的方法计算射电波段多普勒因子.在1969 年Kellermann 和Pauliny[17]认为同步辐射过程的本征亮温度Tb,lim上限可以达到1012K .达到这个温度极限时,同步辐射停止,同时逆康普顿过程开始发生并使电子能量急剧减少.如果在非平稳情况下,相对论电子注入喷流后的最初几天内,喷流亮温度的上限会达到1015K[18].Readhead[19]基于能量均分进行假设:辐射源与磁场之间的能量几乎相等的条件下,本征亮温度的上限应为1011K .逆康普顿过程在同时不满足能量均分和最小能量时才能发生,这就是我们可以观测到亮温度Tb,obs＞1012K 而没有逆康普顿过程的原因.Readhead[19]从VLBI 数据中得到本征亮温度(均分亮温度)Teq≤1011K .多普勒因子用亮温度估计[18-20],Wagner 和Witzel[20]给出了亮温度计算公式

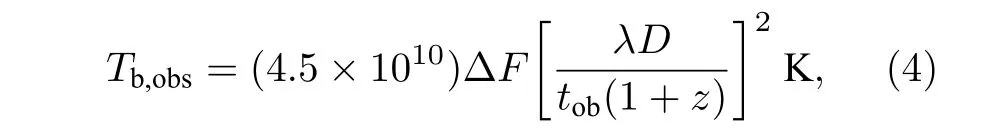
其中Tb,obs为亮温度,ΔF为光变幅度(以Jy 为单位),tob为光变时标(以天为单位),λ为波长(以cm为单位);D为光度距离(以Mpc 为单位).CGRaBS J2345-1555 红移为0.621[21],光度距离为3567 Mpc(引用了网站http://simbad.u-strasbg.fr/simbad/sim-fbasic 中的常数).观测得到的亮温度Tb,obs和多普勒因子δ与均分亮温度Teq有关[18],即

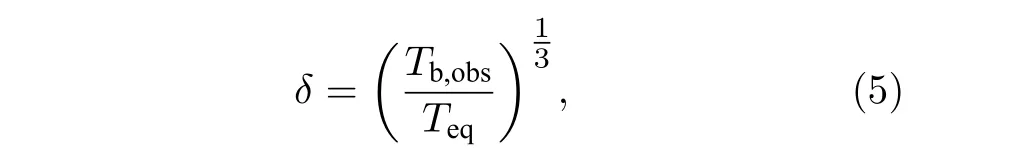
取均分亮温度Teq=5×1010K[20],从而

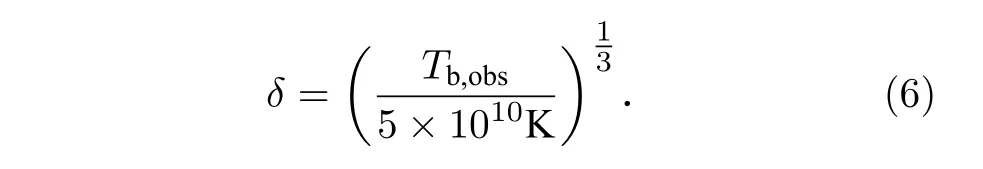
多普勒因子计算结果见表1.

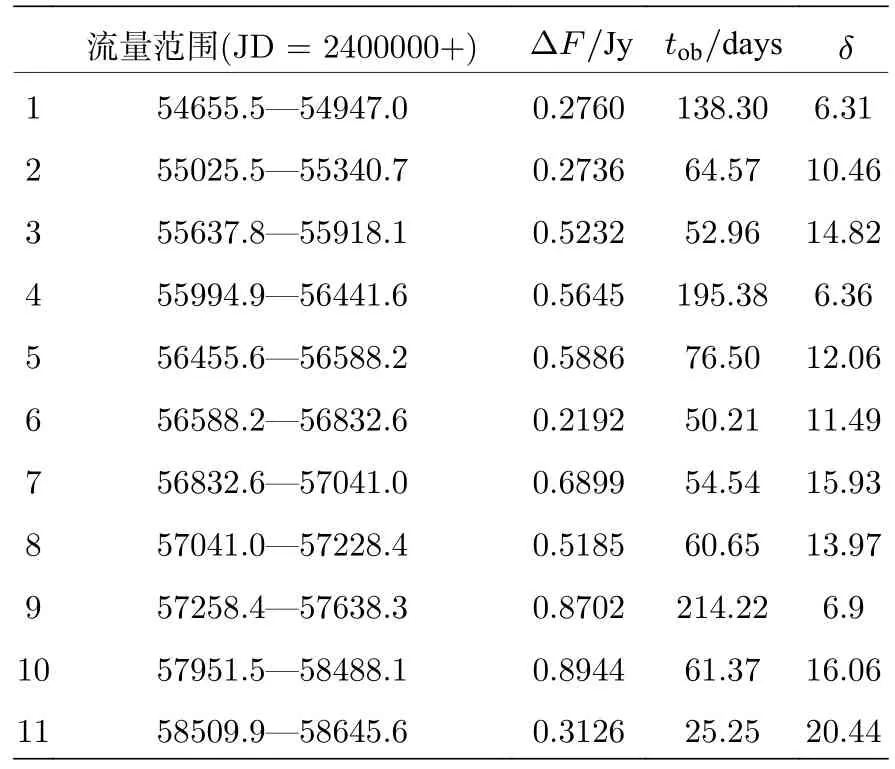
表1 射电波段11 个爆发的多普勒因子Table 1.Doppler factor of 11 bursts in radio band.

5 讨论

射电波段通常解释为自由电子的同步辐射产生.伽马波段通常的解释有:同步自康普顿模型[2]、外康普顿模型[4,5]、质子的同步辐射和质子引发的级联模型[6].如果用同步自康普顿模型解释伽马波段与射电波段的相关性,那么种子光子来源于喷流中的同步辐射,该种子光子与喷流中相对论电子发生逆康普顿散射成为伽马光子,伽马波段与射电波段来自于同一批电子.而伽马波段领先射电波段可以解释为伽马波段的辐射区在喷流的上游,射电波段在下游.Max 等[22]计算了41 个耀变体伽马波段和射电波段相关性,并粗略计算了这两个波段在喷流中的相对辐射位置,同样是伽马波段在上游.

光学波段可能来自同步辐射和吸积盘的热辐射,如果光学波段由热辐射主导,很难解释与射电波段的相关性,但是射电波段和光学波段具有较好的相关性,说明光学波段由同步辐射主导,热辐射贡献很少.射电波段与光学波段的时间延迟同样可以解释为光学波段的辐射区域在上游,射电波段在下游.

没有从离散相关函数计算中得到伽马波段与光学波段的具体相关性,但从离散相关函数计算结果可以看到比较多的点在0.5 以上,不可否认具有相关性,但从前面的分析中可以知道伽马波段与射电波段是同源的.

本文估计的多普勒因子在Liodakis 和Pavlidou[23]所得到结果的范围内,但是精度有待提高,因为我们尽可能多地拟合了视为爆发的峰,峰两端的初始位置和结束位置都是肉眼判断,在数据点很多时不容易判断,但只要在几天的范围内选择初始位置和结束位置对拟合结果影响很小.射电波段55320.7—55537.1 MJD 的时间范围(图1 中编号为0 的矩形)内数据点的起伏很大,不明确对拟合峰的影响,故没有考虑此时间段内的多普勒因子.图1 中编号为12 的矩形中爆发的下降过程可能不完整,故没考虑此时间段内的多普勒因子.

当多普勒因子大于1 即亮温度大于均分温度时会发生多普勒增强效应.表1 中多普勒因子均大于1,说明喷流具有明显聚束效应.从图7 可以看到多普勒因子具有明显的周期性,喷流进动周期约为5.5 年.Caproni 等[24]、Stirling 等[25]计算出耀变体2200+420 的进动喷流中存在周期约2.3 年的成分.Caproni 等[26]用耀变体1553+113 射电波段计算出喷流进动周期为7.5 年.多普勒因子的周期性用喷流进动很容易解释,因为多普勒增强和视角有关,可以更加确信射电波段辐射流量变化来自于喷流.

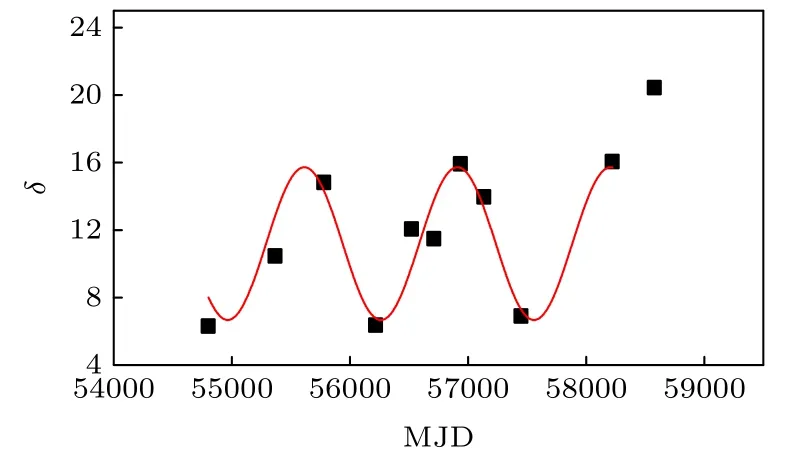
图7 15 GHz 多普勒因子的分布Fig.7.15 GHz Doppler factor distribution.

6 结论

伽马波段与射电波段、射电波段与光学V 波段具有明显的相关性,如果用SSC 模型解释,那么它们来自喷流中的同一批电子,射电15 GHz 和光学V 波段由同步辐射产生,伽马射线由逆康普顿过程产生.伽马波段与光学V 波段没得到具体相关性,可能因为数据不足或不同望远镜之间的仪器误差引起.喷流具有多普勒增强效应,多普勒因子具有一定周期性,可能是喷流进动引起的,说明射电波段流量变化的起因适用于耀变体喷流进动模型.