抑制性自突触诱发耦合Morris-Lecar神经元电活动的超前同步*

丁学利 古华光 贾冰 李玉叶

1) (阜阳职业技术学院基础教学部,阜阳 236031)

2) (同济大学航空航天与力学学院,上海 200092)

3) (赤峰学院数学与计算机科学学院,赤峰 024000)

超前同步(anticipated synchronization,AS)是一种普遍存在的违反直觉的非线性行为:被驱动系统的响应会早于驱动出现,在神经系统的实验中也被发现.本研究揭示了抑制性自突触诱发Morris-Lecar 神经元模型产生AS,给出了产生AS 的条件.在单向兴奋性驱动的双神经元耦合系统,无论神经元是I 型兴奋性还是II 型兴奋性,都只会产生驱动行为在响应之前的滞后同步(delayed synchronization,DS).在被驱动神经元引入抑制性自突触,II 型兴奋性神经元构成的耦合系统会表现出驱动在响应之后的AS;随着自突触电导的增大,DS 会转迁到AS;而I 型兴奋性神经元构成的耦合系统则只会产生DS.进一步,提示了AS 产生与不产生分别与II 型和I 型兴奋性神经元的放电响应特性有关:II 型神经元在抑制性脉冲刺激下放电提前而I 型兴奋性神经元不易产生放电提前.研究结果给出了抑制性自反馈诱发AS 的神经元的兴奋性类型,有助于理解违反直觉的动力学行为—AS,给出了调控AS 的可能手段,为进一步研究AS 提供了方向.

1 引言

同步现象[1,2]在物理和生物等系统中已经被广泛地研究,如完全同步、相位同步、滞后同步(delayed synchronization,DS)和广义同步,及同相同步和反相同步,乃至混沌同步和“超前同步”(anticipated synchronization,AS)[3]等.AS 是一种违反直觉的同步行为:对于单向耦合的驱动和被驱动系统(两个系统相同),如果对被驱动系统施加含有时滞的自反馈,被驱动系统的响应就会发生在驱动系统的驱动之前.这与被驱动系统的响应应该出现在驱动系统的刺激之后的常规概念不同.近期,神经系统的众多违反直觉的非线性现象及动力学机制被广泛研究[4-8],拓展了非线性动力学的内涵.揭示AS 这一违反直觉的非线性行为的特征和机制,也是亟待解决的科学问题.

能产生AS 的单向耦合的两个相同的动力系统[3,9-12]的数学模型如下:

方程(1)对应驱动系统,其中S为系统的变量,f(·)为系统的演化函数.方程(2)等号右侧第1 项对应被驱动系统,其中R为系统的变量,f(·) 为系统的演化函数;方程(2)等号右侧第2 项对应驱动系统对被驱动系统的单向耦合或激励 (K是耦合矩阵).如果在耦合中引入被驱动系统的自反馈延迟调控KR(t-ts),ts代表时滞,则耦合系统变为

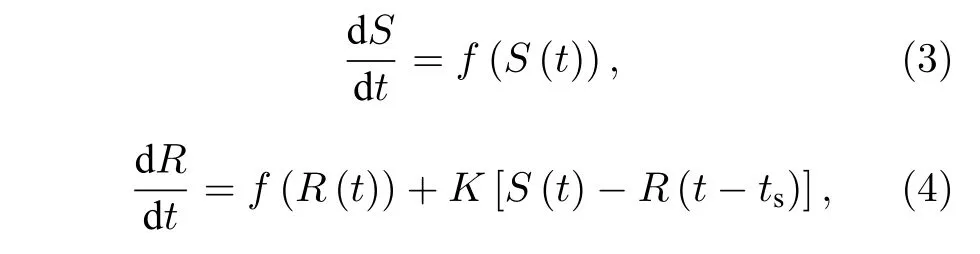
若耦合系统(3)和(4)出现R(t)=S(t+ts) 的解(ts＞0),就意味着出现了AS 现象.这是因为R(t)=S(t+ts)(ts＞0)说明行为R在被驱动系统的t时刻出现,而在驱动系统则是在t+ts时刻出现,意味着驱动系统的行为R提前传递到了被驱动系统.因此,AS 是一种违反直觉的非线性行为.AS现象在很多理论和实验研究中得到了验证[3,9-39].例如,在单向耦合的半导体激光器延迟光电反馈的实验中,不同的传输时间和反馈延迟时间,激光器可以出现AS 或DS 现象[13].DS 就是被驱动系统的响应出现在激励之后的同步行为.

在神经元理论模型的研究中也发现了AS 现象.单向耦合的两个FitzHugh-Nagumo 神经元模型,在1 个共同的非周期激励下实现了AS,即使受到了白噪声激励,AS 仍然存在[14].在由兴奋性突触耦合的Hodgkin-Huxley 神经元模型中,也发现了AS 的存在,膜电位的去极化水平决定了激励和响应间的相位差[15].在两个Hodgkin-Huxley 神经元模型经由单向化学突触耦合构成的驱动-被驱动结构中,引入1 个中间神经元、且该中间神经元介导的延迟负反馈会作用到被驱动系统,当被驱动系统的频率大于驱动系统的频率时,该三神经元模型可以表现出AS.进一步,揭示了抑制性突触电导对从DS 到AS 的转迁过程中起到重要作用[16].研究还表明,AS 对噪声[17]和spike-timing 依赖的突触可塑性[18]具有鲁棒性.在具有突触时滞和记忆效应的两个Rulkov 映射神经元模型也发现了AS[19].两个单向耦合的Hindmarsh-Rose 神经元模型,当被驱动神经元的平均放电频率略大于驱动神经元的平均放电频率时,也存在AS[20].最近,在两个完全相同的Izhikevich 神经元模型单向兴奋性驱动构成的系统中,当被驱动神经元引入抑制性自突触后,会诱发AS,就是被驱动神经元的动作电位会出现在驱动神经元的之前,并且时间间隔是稳定的[21].当抑制性自突触电导增大时,通常会发生从DS (被驱动神经元的动作电位会出现在驱动神经元的之后)到AS 的转迁.当模型参数在生理范围内变化时,这种现象是鲁棒的.当兴奋性耦合较小且抑制性自突触电导较大时,系统会出现相位漂移(phase-drift,PD)现象,就是驱动神经元和被驱动神经元的动作电位的先后顺序和时间间隔不稳定的现象.除了理论研究,AS 在视觉认知实验的脑电中被发现.猴的认知实验和人的视觉刺激-运动或意识反应的认知任务实验中,发现了脑电存在AS[22-25].脑区间的信息流是从后顶叶皮质(驱动)到初级运动皮层和初级体感皮层(被驱动),但是后顶叶皮质脑电却发生在初级运动皮层和初级体感皮层的脑电之前(脑电主频出现负相位差).该研究用电极同步记录脑的不同部位的脑电、对任意两个电极之间的脑电进行Granger 因果分析和频谱分析获得结果.

在神经元的理论研究中,AS 与抑制性作用包括抑制性自突触建立了联系[21].在单向兴奋性耦合的双神经元系统,被驱动神经元引入抑制性自突触,被驱动神经元的放电提前到驱动神经元的放电之前,引起的响应早于刺激的AS[21]现象.但是,对于抑制性作用比如抑制性自突触诱发的AS 的动力学机制,尚缺乏全面和深入理解解释,比如,什么动力学性质的神经元可以产生AS? 实际上,AS是放电的相位变化的问题,抑制性自突触诱发AS就是抑制性自突触电流的作用会引起放电提前.而最近的研究[5]发现抑制性刺激下II 型兴奋性/Hopf分岔的神经元放电能够提前.因此,假若抑制性刺激不能诱发I 型兴奋性/不变圆上的鞍结分岔的神经元放电提前,则神经元的II 型兴奋性可能是抑制性自突触诱发AS 的动力学机制.本文立足于回答这一问题.

基于上述分析和认识,本文选取具有I,II 型兴奋性的Morris-Lecar (ML)模型,研究抑制性自突触诱发ML 模型的AS 的特征以及AS 产生的神经元的兴奋性类型.结果发现,对II 型兴奋性神经元,抑制性作用能够引起放电提前,而抑制性自突触确实能诱发AS,并获得AS 存在的参数区间;而对I 型兴奋性神经元,抑制性作用不易诱发单神经元放电提前,抑制性自突触也不能诱发耦合神经元的AS.该结果揭示了抑制性作用诱发的违反直觉的动力学行为—AS 的动力学特征,给出了AS产生的神经元的兴奋性条件,为进一步研究神经系统的AS 指明了方向,为认识和调控神经系统的AS 现象奠定了基础.

2 神经元模型

2.1 Morris-Lecar 模型

ML 模型是研究神经元I,II 型兴奋性的常用模型.本文研究的神经元耦合系统是由两个相同的ML 神经元模型组成,其ML 单神经模型[5,40,41]为

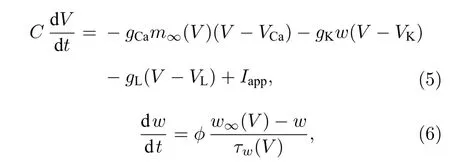
其中,V和w分别为膜电压和激活变量;C为膜电容;(5)式等号右边第1—4 项分别为钙电流、钾电流、漏电流和外激励电流Iapp;钙电流的最大电导和反转电位分别为gCa和VCa;钾电流的最大电导和反转电位分别为gK和VK;漏电流的最大电导和反转电位分别为gL和VL;ML 模型中与电压相关的速率常数为

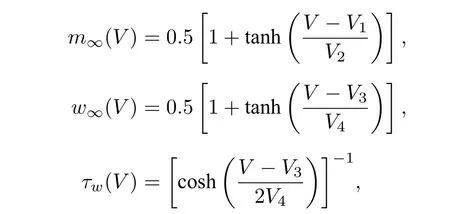
V1—V4为拟合参数;φ为时间尺度比率.由于在不同参数下,ML 模型会表现出不同的放电行为.本文选取能表现I,II 型兴奋性特点的参数,如表1所列.

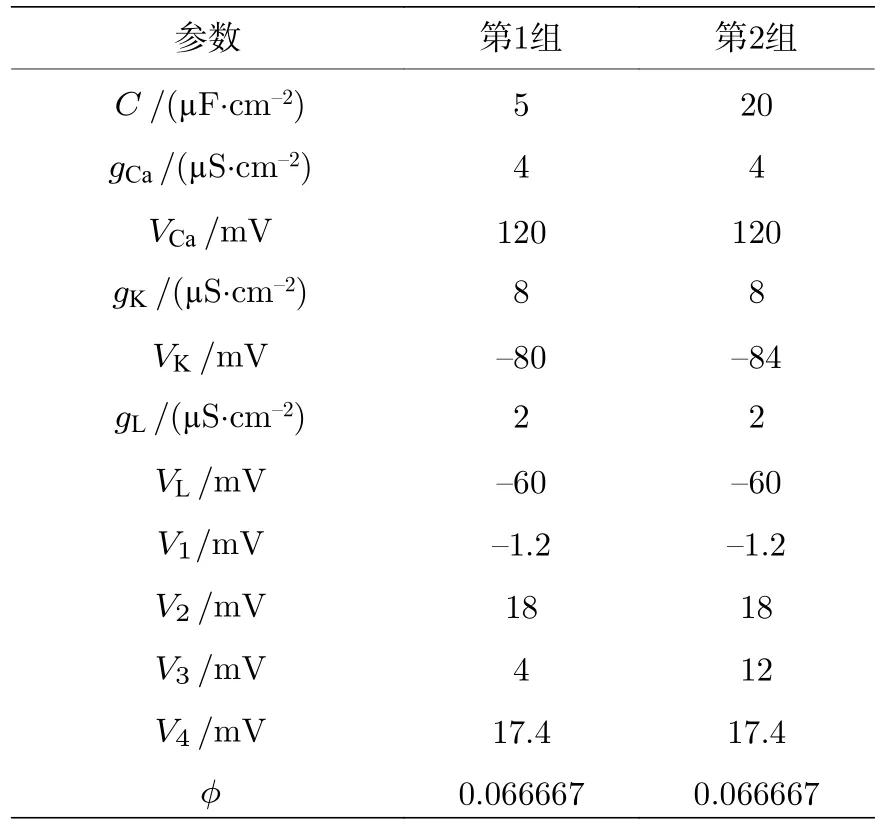
表1 ML 模型的参数值Table 1.Parameter values of ML model.

2.2 突触动力学

由两个相同的ML 神经元模型和化学突触组成的耦合系统,其驱动(S)神经元的脉冲活动由下面的方程描述:

被驱动(R)神经元与驱动神经元有类似的方程,但还有两个突触电流,分别是来源于驱动神经元的兴奋性突触电流(IE)和自身的抑制性自突触电流(II),具体方程如下:

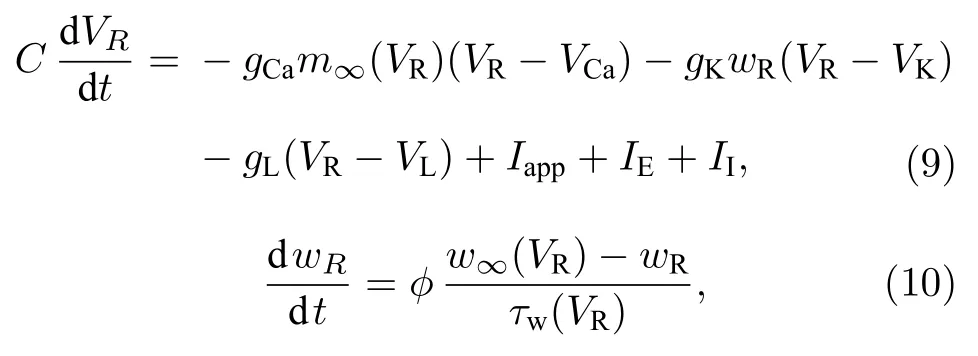
其中,来源于S神经元兴奋性突触电流为

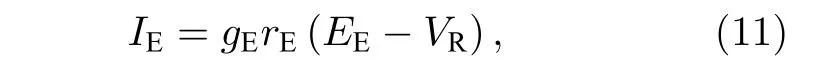
而来源于自身的抑制性自突触电流为

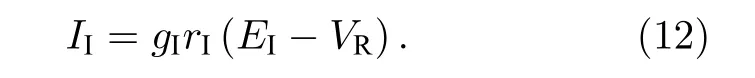
这里,gE和gI分别是兴奋性突触电导和抑制性自突触电导,EE和EI分别是兴奋性突触和抑制性自突触的反转电位.变量ri(i=E,I)为突触受体,其一阶动力学模型如下[21]:

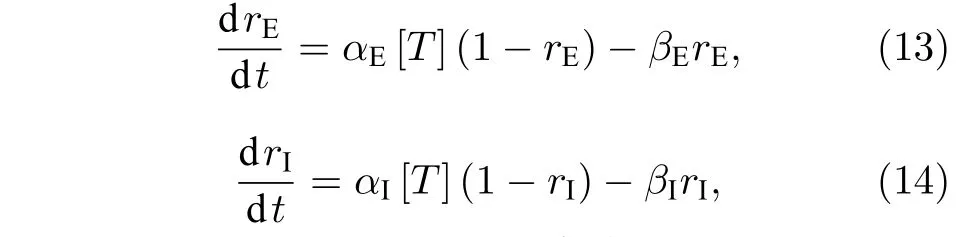
式中,αi和βi(i=E,I)是速率常数,[T] 是突触间隙内的神经递质浓度,其为依赖于突触前电位Vpre的函数,

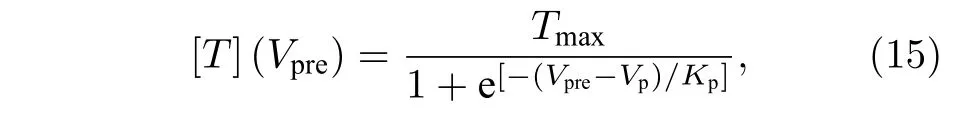
其中,Tmax是 [T]的最大值,Kp表示sigmoid 函数的陡度,Vp为函数处于半激活时的值.αE,βE,αI和βI是速率常数.突触电流的参数设置如表2 所列,其中第1 组参数与ML 模型的II 型兴奋性参数(表1 的第1 组参数)匹配使用;第2 组参数与ML 模型的I 型兴奋性参数(表1 的第2 组参数)匹配使用.

表2 突触的参数值Table 2.Parameter values of synapse.

3 结果

3.1 II 型兴奋性神经元

3.1.1 抑制性刺激可以诱发对应II 型兴奋性的放电提前

单神经元的ML 模型在表1 的第1 组参数下,存在极限环的鞍结分岔(Iapp≈44.65 μA/cm2)和亚临界Hopf 分岔(Iapp≈45.2335 μA/cm2),对应着神经元的II 型兴奋性.本文选取Iapp=46 μA/cm2的稳定放电,此时放电周期T0≈52.87 ms.

相位响应曲线[5,41-43](phase response curve,PRC),可用来描述兴奋性和抑制性脉冲如何调控神经元的放电相位,其定义如下:

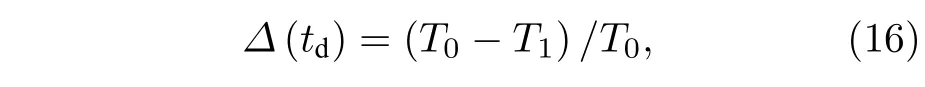
其中,T0为没受外激励时稳定的放电周期;td为外激励从峰值时刻到开始作用时刻的时间;T1为受外激励后峰值出现的时刻(图1(a)).例如,在ML模型的II 型兴奋性参数下,无外激励刺激的放电(图1(a)黑线)周期T0≈52.87 ms.在td=20 ms处,施加负向方波脉冲刺激(幅值A=—7 μA/cm2,宽度d=4 ms),扰动后的T1≈51.69 ms (图1(a)红线).由(16)式计算得Δ(20)≈0.0223 ＞ 0,说明扰动后的放电提前.按此方法计算不同td的Δ,则可得PRC (图1(b)红色点线).从图1(b)可知,在相同的抑制性方波脉冲宽度(d=4 ms)下,不同的幅值(A=—3,—5,—6,—7 μA/cm2)下对应的PRC具有相同的性质.当27.36 ms ＜td＜ 52.73 ms 时,Δ＜ 0,扰动后的放电延后;当0 ＜td＜ 27.36 ms时,Δ＞ 0,扰动后的放电提前.图1(c)是图1(b)的局部放大图,其中Δ＞ 0 的最大幅值达到10—2量级.

图1(a)中放电提前也可以利用V-dV/dt相平面进行分析,如图1(d)—(f) 所示.在图1(d)中,红线对应图1(a)中有抑制脉冲刺激的放电在(V,dV/dt)平面内的轨迹,对应的时间是从刺激开始到动作电位峰值;黑线对应图1(a)中没有抑制脉冲刺激的放电在(V,dV/dt)平面内的轨迹,对应的时间是从刺激开始到动作电位峰值.图1(e)和图1(f)为图1(d)在不同部位的放大.刺激结束时刻对应着dV/dt的正向的突然变化,如图1(e)中的箭头所示.刺激结束后到动作电位峰值,红线总在黑线之上,如图1(d)—(f)所示.这说明相同的V值下,刺激后的dV/dt值总大于刺激前,因此,刺激后的动作电位峰值会提前.

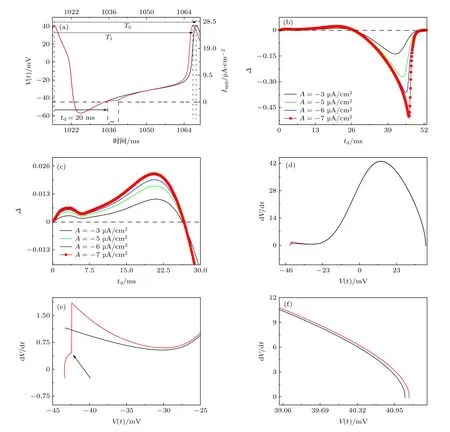
图1 II 型兴奋性ML 模型在抑制性刺激下的放电 (a)与无刺激的放电(黑线)相比,负向方波脉冲(虚线,幅值A=—7 μA/cm2,宽度d=4 ms)诱发的放电(红线)提前;(b)不同的负向方波脉冲(宽度d=4 ms)诱发的PRC;(c)图(b)的局部放大图;(d)黑线和红线分别对应图(a)的黑线和红线(V,dV/dt)的相轨迹,从脉冲刺激结束到各自的动作电位峰值;(e)图(d)的局部放大图(从脉冲刺激开始到V=—20 mV,箭头代表刺激结束);(f)图(d)的局部放大图(动作电位峰值前)Fig.1.Firing of ML model with type II excitability under the action of inhibitory stimulation:(a) Compared with no stimulations(black solid line),firing (red line) induced by negative square pulse (dashed line,amplitude A=—7 μA/cm2,width d=4 ms) is earlier;(b) PRC induced by negative square pulses with different strengths (width d=4 ms);(c) locally enlargement of panel (b);(d) black and red curve correspond to trajectory in (V,dV/dt) plane of black and red curve of panel (a),respectively (from begging time of the pulse stimulation to peak of the action potential);(e) enlargement of panel (d) (from begging time of the pulse stimulation to —20 mV);(f) enlargement of panel (d) (phase before the peak of action potential).

3.1.2 耦合神经元模型可以产生DS,AS和PD

首先用ML 模型II 型兴奋性的参数(表1 和表2 的第1 组参数),探索DS,AS 和PD 的现象.抑制性自突触电导固定为gI=0.3 μS/cm2,在不同的兴奋性电导值gE下,模型可以表现出如图2 所示的不同同步行为.为了描述每个现象,定义为驱动神经元的膜电位在第i个周期(即第i个峰时)的时间,而为对应的被驱动神经元的峰值时间.S 和R 神经元之间的尖峰计时差τ定义为

根据τi随着i增大表现出的不同动力学性质来区分DS,AS 和PD.

如果τi随着i的增大收敛到一个正的常数τ时,即τ ＞0,则系统表现DS,如图2(a1)所示(gE=1.8 μS/cm2).从起始到达稳态,驱动神经元放电(黑)在前、被驱动神经元放电(红)在后.图2(a1)中有1 个时间的间断符.随着时间的演化和i的增大,τi逐步降低,最终收敛到1 个稳态正值τ ≈0.82 ms,如图2(a2)所示,上横坐标代表时间,下横坐标代表第i个放电周期.

如果τi随着i的增大收敛到1 个负的常数τ时,即τ <0,则发生 AS.放电起始时是驱动神经元放电(黑)在前、被驱动神经元放电(红)在后,经过一段时间的演化(间断符所示),变为驱动神经元放电(黑)在后、被驱动神经元放电(红)在前,如图2(b1)所示(gE=0.1 μS/cm2).相应地,随着时间的演化和i的增大,τi从正值逐步降低变为负值、最后收敛到1 个稳态负值τ ≈—11.21 ms,如图2(b2)所示,上横坐标代表时间,下横坐标代表i.

如果τi没有收敛到1 个固定的值,该系统处于PD 状态,如图2(c1)和图2(c2)(gE=0.03 μS/cm2)所示.τi的变化随着时间表现出周期性,1 个周期内的τi从约28.62 ms 降低到约—23.91 ms.该降低是由抑制性自突触引起放电提前引起的.

图2 抑制性自突触诱发II 型兴奋性ML 神经元模型产生的3 种动力学行为(gI=0.3 μS/cm2).DS (gE =1.8 μS/cm2):(a1)驱动(黑)和被驱动(红)神经元的膜电位;(a2)两神经元放电时间间隔的变化.AS (gE =0.1 μS/cm2):(b1)驱动(黑)和被驱动(红)神经元的膜电位;(b2)两神经元放电时间间隔的变化.PD (gE =0.03 μS/cm2):(c1)驱动(黑)和被驱动(红)神经元的膜电位;(c2)两神经元放电时间间隔的变化Fig.2.Three dynamic behaviors induced by inhibitory autapse (gI =0.3 μS/cm2) in the ML neuron model with type II excitability.DS (gE =1.8 μS/cm2):(a1) Membrane potential of driving (black) and driven (red) neurons;(a2) change of time interval between spikes of two neurons.AS (gE =0.1 μS/cm2):(b1) Membrane potential of driving (black) and driven (red) neurons;(b2) change of time interval between spikes of two neurons.PD (gE =0.03 μS/cm2):(c1) Membrane potential of driving (black) and driven (red)neurons;(c2) change of time interval between spikes of two neurons.

3.1.3 没有抑制性自突触耦合神经元不产生AS

ML 模型在II 型兴奋性的参数(表1 和表2的第1 组参数)下,若抑制性自突触电导设为gI=0 μS/cm2,则随着兴奋性突触电导值gE的增加,τ始终大于0,如图3 所示.说明在没有抑制性刺激耦合的神经元将不会产生AS.

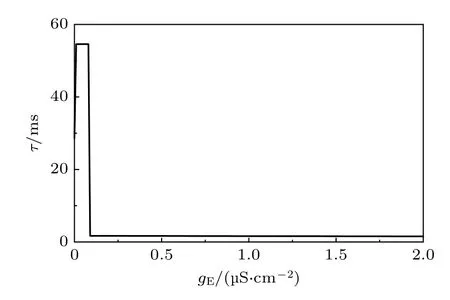
图3 单向耦合II 型兴奋性ML 模型在没有抑制性自突触(gI=0)时产生DS (两神经元放电时差在不同兴奋性电导下大于0,即 τ ＞ 0)Fig.3.DS of type II ML model with unidirectional excitatory coupling and without inhibitory autapse (gI =0) (time interval between spikes of the two neurons is larger than 0 at different values of conductance of excitatory synapse,i.e.τ＞ 0).

3.1.4 引入抑制性自突触后耦合神经元产生AS

对被驱动神经元引入抑制性自突触,会引起AS (τ＜ 0),如图4 所示.红线和蓝线分别表示固定gI=0.8 μS/cm2和gI=1.5 μS/cm2时 产 生AS,小于三角符号标记的gE范围代表PD.gI越大,τ的绝对值越大.黑线代表gI=0.2 μS/cm2时,随着gE的增大,AS 可以变为DS (τ＞ 0);而随着gE的降低,AS 变为PD (位于三角符号标记以左).

图4 不同抑制性电导 gI 下兴奋性耦合的II 型兴奋性ML 模型的AS (两神经元放电时间间隔 τ随 gE 的变化).τ＞ 0 表示DS 状态,τ ＜ 0 代表AS 状态.三角符号标记以左出现PDFig.4.Anticipated synchronization of type II ML model with excitatory coupling at different values of the conductance of inhibitory autapse (changes of time intervalτ between spikes of two neurons with respect to gE).τ ＞ 0 and τ ＜ 0 represent DS and AS states,respectively.PD locates left to the triangle.

3.1.5 在(gI,gE)平面上,AS 位于DS 和PD 之间

为了全面地展示兴奋性单向耦合的II 型兴奋性ML 模型产生AS,DS 和PD 参数的范围,图5给出了两神经元放电时间间隔τ在参数空间(gI,gE)的分布.图5(a)的红色区域表示DS (τ＞ 0),绿色区域表示AS (τ＜ 0),黑色区域表示PD (τ的值不稳定).从DS 到AS 转变的分界线可用线性关系gE/gI≈3.444 来近似,而从AS 到PD 转变的分界线可用线性关系gE/gI≈0.137 来近似.

图5 单向兴奋性耦合的II 型兴奋性ML 模型的3 类行为在参数平面(gI ,gE)的分布 (a)两神经元放电间隔 τ 的分布,红、绿和黑色分别表示DS (τ ＞ 0),AS (τ ＜ 0)和PD (τ 的值不稳定);(b)两神经元放电间隔 τ 的量值Fig.5.Distribution of three behavior in parameter plane(gI ,gE) of the type II ML model with unidirectional excitatory coupling:(a) Distribution of time interval τ between spikes of two neurons,red,green,and black indicate DS(τ ＞ 0),AS (τ ＜ 0),and PD (the value of τ is unstable),respectively;(b) values of time interval τ .

在DS 和AS 区域,τ的量值的分布如图5(b)所示.对于AS,固定gE,τ的绝对值随着gI的增大而增大;在DS 区域中,固定gE,τ的值随着gI的增大而减小(图5(b)).

3.2 I 型兴奋性神经元

3.2.1 抑制性刺激不易诱发对应I 型兴奋性的放电提前

在表1 第2 组参数下,ML 模型在Iapp≈39.96 μA/cm2处产生不变圆上的鞍结分岔,对应I 型兴奋性.本文选取在Iapp=46 μA/cm2处的稳定放电,对应放电周期T0≈92.27 ms.

与II 型兴奋性PRC 的定义类似,也可得到I 型兴奋性的PRC,如图6(a)所示.负向脉冲刺激诱发I 型兴奋性的PRC 几乎全负,如图6(a)所示,与大家熟知的正向脉冲诱发的PRC 几乎全正且关于Δ=0 是对称的.在相同的抑制性方波脉冲宽度(d=4 ms)下,不同的幅值(A=—1,—3,—5,—7 μA/cm2)下对应的PRC 具有相同的性质.Δ＜ 0,意味着刺激后的放电延后.图6(a)中出现了小部分Δ＞ 0 的情况,其局部放大图,如图6(b)所示.图6(a)与图1(b)中Δ＞ 0 的幅值差别还是比较大的(见放大图),图6(b)中Δ＞ 0 的幅值的最大值大约是0.0038,并且其参数区间较窄,在当前的突触参数下,抑制性电流不容易作用在这个窄的区间,因而不易产生AS.

图6(a) 不同抑制性方波脉冲(宽度d=4 ms)刺激诱发I 型兴奋性ML 模型的PRC;(b)图(a)的局部放大图Fig.6.(a) PRC induced by inhibitory square pulses (width d=4 ms) stimulation in ML model with type I excitability;(b) locally enlarged of panel (a).

3.2.2 没有抑制性自突触的耦合神经元系统不易产生AS,只产生DS

ML 模型在I 型兴奋性的参数(表1 和表2 的第2 组参数)下,若抑制性自突触电导为gI=0 μS/cm2,则随着兴奋性电导值gE的增大,τ始终大于0,如图7 所示.说明在没有抑制性自突触时,耦合神经元系统将不会产生AS,只产生DS.

3.2.3 引入抑制性自突触后耦合神经元系统不易产生AS

由图7 可知,在没有抑制性自突触时,耦合神经元将不会产生AS.现引入抑制性自突触,看是否会产生AS.例如,取抑制性自突触电导gI=0.2 μS/cm2和兴奋性耦合电导gE=0.02 μS/cm2,如图8(a1)和图8(a2)所示,其放电时间序列(驱动神经元放电(黑)在前、被驱动神经元放电(红)在后)和两神经元的放电时间间隔τ ≈4.25 ms,均说明只产生了DS.若兴奋性电导为gE=0 μS/cm2,只有抑制性自突触电流,此时系统表现PD,如图8(b1)和图8(b2)所示.τi的变化随着时间表现出周期性,1 个周期内的τi从约7.73 ms 延长到约106.83 ms.延长是因为该结果是在没有抑制性自突触流,只有兴奋性突触流的情况下产生的.因此,时间延长是由兴奋性突触流引起放电延后引起的.无论如何引入抑制性自突触电流,耦合神经元的行为均不易产生AS.

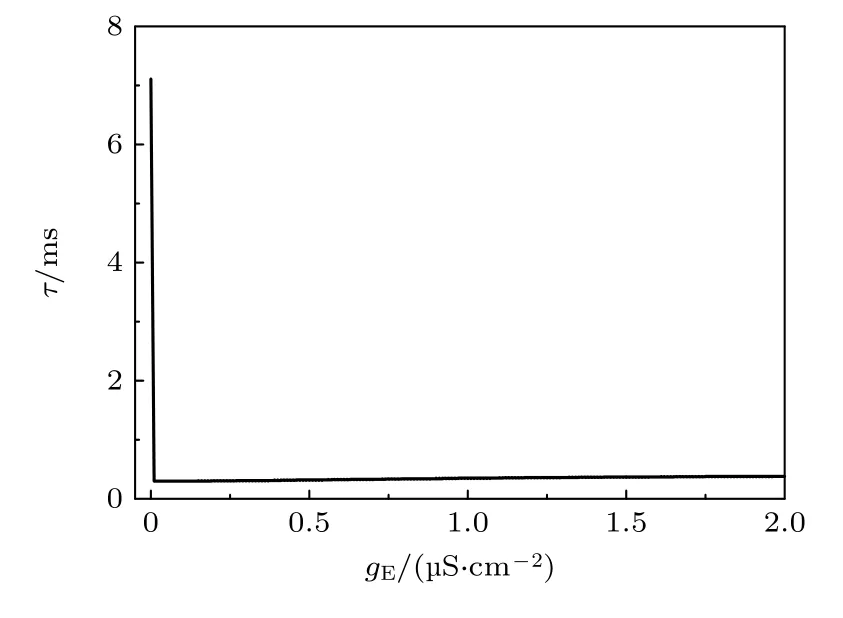
图7 单向耦合I 型兴奋性ML 模型在没有抑制性自突触电导(gI =0 μS/cm2)时产生DS (两神经元放电时差在不同兴奋性电导下大于0,即 τ ＞ 0)Fig.7.DS of type I ML model with unidirectional excitatory coupling and without inhibitory autapse (gI =0) (time interval between spikes of the two neurons is larger than 0 at different values of conductance of excitatory autapse,i.e.τ＞ 0).

图8 抑制性自突触诱发I 型兴奋性ML 神经元模型产生的2 种动力学行为(gI=0.2 μS/cm2).DS (gE =0.02 μS/cm2):(a1)驱动(黑)和被驱动(红)神经元的膜电位;(a2)两神经元放电时间间隔的变化.PD (gE =0 μS/cm2):(b1)驱动(黑)和被驱动(红)神经元的膜电位;(b2)两神经元放电时间间隔的变化Fig.8.Two dynamical behaviors induced by inhibitory autapse in the ML neuron model with type I excitability (gI =0.2 μS/cm2).DS (gE =0.02 μS/cm2):(a1) Membrane potential of driving (black) and driven (red) neurons;(a2) change of time interval between spikes of two neurons.PD (gE =0.0 μS/cm2):(b1) Membrane potential of driving (black) and driven (red) neurons;(b2) change of time interval between spikes of two neurons.

图9 是固定抑制性电导gI,两神经元放电的时间间隔τ随兴奋性电导gE的变化.黑、红和蓝线分别表示固定gI=0.2 μS/cm2,gI=0.8 μS/cm2和gI=1.5 μS/cm2时的τ值.τ＞ 0 表示DS 状态,三角形标记以左代表PD.从图9 可知,在3 个抑制性电导下,除在gE=0 处产生了PD,其余均产生了DS,没有AS 产生.

图9 不同抑制性电导 gI 下兴奋性耦合I 型兴奋性ML 模型的DS (两神经元放电时间间隔 τ随 gE的变化).τ ＞ 0 表示DS 状态,三角符号标记处出现PDFig.9.DS of the type I ML model with excitatory coupling at different values of conductance of inhibitory autapse(changes of time interval τ between spikes of the two neurons was with respect to gE).τ ＞ 0 represents DS state,and the phase-drift locates to the triangle.

为了更好地展示产生DS 参数的范围,图10给出了两神经元放电时差τ在参数空间(gI,gE)的分布.如图10(a)所示,除在gE=0 处出现了PD(黑色区域),其余存在DS 的分布区域(红色区域,τ＞ 0).在DS 区域中,固定gI,τ的值随着gE的增大而减小,如图10(b)所示.

图10 单向兴奋性耦合的I 型兴奋性ML 模型的DS 在参数空间(gI ,gE)的分布 (a)两神经元放电间隔 τ 的分布;红和黑分别表示DS (τ ＞0)和PD (τ 的值不稳定)区域;(b)两神经元放电间隔 τ 的量值Fig.10.Distribution of DS in parameter plane (gI ,gE) of type I ML model with unidirectional excitatory coupling:(a) Distribution of time interval τ between spikes of two neurons,red and black indicate DS (τ ＞ 0) and PD (the value of τ is unstable),respectively;(b) values of time interval τ .

4 结论

AS 是违反直觉的重要的非线性动力学现象,揭示其动力学特性和产生条件对于丰富非线性科学的内涵和认识神经系统中的实验现象具有重要的意义.本文揭示了抑制性自突触诱发单向兴奋性耦合的双神经元模型(ML 模型)产生的AS,取得了以下的进展:

1)将文献[21]中的Izhikevich 模型换为具有I,II 型兴奋的ML 神经元模型,施加抑制性脉冲刺激,II 型兴奋性神经元可以产生放电提前,而I 型兴奋性的神经元不易出现放电提前.研究结果揭示了抑制性作用下的神经元放电的相位变化,结合大家熟知的兴奋性作用诱发的放电相位的变化(与抑制性作用的相反),全面认识了不同激励下的神经放电的相位变化.

2)在单向耦合的两个完全相同的ML 神经元模型中,若只有兴奋性耦合流,没有抑制性自突触流,无论神经元是I 型兴奋性还是II 型兴奋性,耦合系统都只会产生DS,而不易产生AS.

3) 在被驱动神经元引入抑制性自突触后,随着抑制性自突触电导的增大,II 型神经元则会表现出从DS 到AS 的转迁.AS 的出现是因为抑制性作用引起了放电提前,使得被驱动神经元的放电提前到驱动神经元的放电之前,诱发了AS.而I 型神经元只会产生DS,这是因为抑制性作用不能引起被驱动神经元的放电提前.研究结果给出了AS 这一违反直觉的非线性行为的产生的单神经元的兴奋性条件,从而对神经系统中AS 这一有趣的问题的研究起到推动作用.

本文研究的AS 是神经系统的抑制性反馈和兴奋性耦合的综合作用结果.首先,进一步拓展了神经系统的复杂时空动力学,在众多耦合神经系统复杂时空动力学基础上[44-49],进一步探讨抑制性作用对网络时空行为的影响及其相关的生理功能.其次,AS 是违反直觉的非线性现象,与近期的违反直觉的非线性行为[4-8,47,50]一起,丰富了非线性动力学的内涵,今后要进一步探讨抑制性作用对AS 的全面影响,有助于理解AS 在神经系统中的动力学机制及功能意义.最后,本研究结果提示了抑制性自突触的潜在功能,是对诸多自突触的功能[4-8,47,50-52]的补充,今后应进一步加强自突触的动力学行为及功能的研究.