巧用旧知学新知

刘娟

案例1 “倍”的认识

分析：乘法口诀其实就是倍的内容，这是学生熟练掌握的知识。教学就以乘法口诀为教学起点，逐步展开。

第一步，根据乘法口诀，引出“倍”的概念。

教师从四九三十六，4×9=36，得出36是4的9倍，也可以说36是9的4倍。学生举例并仿照这种形式说一说，如7×8=56，56是7的8倍，56是8的7倍。

这样引入“倍”，学生一点都不陌生，更有亲切感。

第二步，看图、画图表现“倍”。

出示图，并提问：图中下一行的△是上一行△的多少倍？你是如何想的？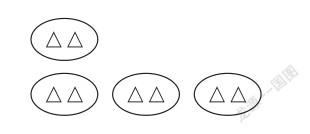

学生很快想到两种思路：一是下一行有3个圈，上一行有1個圈，那么下一行的△是上一行的3倍。二是上一行有2个△，下一行有6个△，那么下一行的△是上一行的3倍。用式子分别表示为：3÷1=3，6÷2=3。

用图表示两个数（量）之间的倍数关系，一看即明，学生易懂。从两种思路中发现，画圈是个好办法，可以将倍数关系直接看出来。

第三步，用算式计算与“倍”有关的数。

经过乘法口诀、图示两个环节教学，学生对“倍”有了初步认识。至此，需要用算式表达练习倍的问题。如，5的3倍是多少？28是7的几倍？

学生对有图的倍数关系，还容易想到如何解决，但对这样的文字表述，一时难以适应，必须通过适当的训练题才能达到理解倍的目的。教师可以根据列出的式子，请学生说说算式中，谁是谁的几倍。例如，5×3=15，表述为5的3倍是15，也可以说15是5的3倍。

从乘法口诀到倍，只是算式中各个数名称的改变，数学的本质意义没有改变。抓住了这一点善加引导，学生以乘法口诀这个非常熟悉的内容为切入点，就可以自然进入到“倍”的学习中。

案例2 平行四边形面积公式的推导

对于平行四边形面积公式的推导教学，笔者采用了一个特殊的教学方法。

首先，出示一个平行四边形，问：它的面积是多少平方厘米？解决的办法就要从求面积的已有方法中去寻找。已有方法只有数格子、长方形面积公式。长方形面积公式是数格子得出的，那么平行四边形面积就要进一步推导了，想办法转化为长方形，那就好了。

如何将平行四边形转化为长方形？见下图。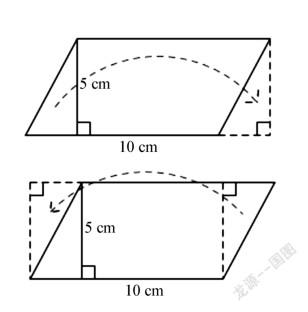

这样，平行四边形面积是10×5=50（cm2）。

其次，推导平行四边形面积公式。由上面的转化图，很容易得到：平行四边形的底是长方形的长，高是长方形的宽，平行四边形面积=长方形面积，也就是：平行四边形面积=底×高。

推导出的平行四边形面积公式，今后可以作为工具使用，用来推导其他面积公式，如三角形面积、梯形面积、圆面积公式。

数学学习是一个“前赴后继”的过程，将旧知识换一种表述，进行形式上的变换，或者添一点新元素就成为新知识。