概念教学：基于有效追问的教学探索

王泽扬

数学课堂是思维的课堂，思维的发展需要有效碰撞。概念课是数学课中的重要组成部分，概念课能否达成预期的教学目标，突出重点，突破难点，关键在概念的生成。概念的生成是自然的，是流畅的。学生需要了解这个数学概念是什么，源自哪里；了解研究它有何意义和作用；了解它的概念的内涵与外延；了解如何证明它的正确性、良定性、充要性。在课堂上，学生是教学的主体，教师是主导，在知识建构的过程中，教师要引导学生，主动探索知识。要使概念生成更加清晰、自然、逻辑通顺、条理清晰，需要教会学生如何追问。因此，概念的生成离不开有效追问。

追问是在提问的基础上进行再次发问，目的是使学生正确、准确、深度理解知识，能够解决问题。追问是对初次提问的补充、深入、拓展或修改。师生之间的有效追问，不仅能凸显教师主導、学生主体的地位，还能有效开展学生活动和数学建构，在对话和沟通中，明晰概念逐渐。

一、 概念教学的有效预设

空间向量基本定理是苏教版选修2—1高中数学教科书第三章的3.1.3小节的内容。从地位上看，空间向量基本定理在教科书的本章中的位置是至关重要的—它需要解决必要性、合理性和严谨性共三个方面的问题，从而将概念生成得饱满而充实。从功能上看，它为下面学习空间向量的坐标表示与坐标运算、用坐标的思想解决立体几何问题提供了了理论支持。从结构上看，它上接共线向量基本定理、共面向量定理，同时推广了平面向量基本定理，是数学中从低维到高维抽象的一个缩影。从功能上看，它将数学抽象、逻辑推理、数形结合、直观想象、数学运算等核心素养孕育其中，能让学生在空间向量这一个知识载体中，体会抽象而又伟大的数学世界的奥妙。

本节课教学之前，学生也已开始学习空间向量的有关内容。空间中，类比平面向量基本定理，又会得到怎样的结论呢？它又有怎样的作用呢？学生带着这一问题串，不断探索数学知识。

基于以上分析，本节课的教学目标确定如下：理解空间向量基本定理及其推论，知道空间任意一个向量可以用不共面的三个已知向量线性表示，而且这种表示是唯一的；在简单问题中，会选择适当的基底来表示任一空间向量。

二、 概念生成中有效追问的设计与实施

教学片断：在竖直平面内，炮弹、喷出的水做抛体运动。

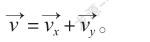
问题1：从数学的角度，哪一个定理与这个过程密切相关？

学生A：之所以这个被称为平面向量基本定理，是因为对于平面内任意一个向量，都可以用这个平面内任意两个不共线的向量来表示。教师：下面我们将这个问题推广到空间中。

设计意图：从现实情境出发，让学生感受之前学习过的平面向量基本定理与今天所学内容之间的紧密联系，感受平面向量基本定理的合理性，同时渗透推广、类比的思想。

问题2：垒球、铁饼、标枪被投掷后在空间中产生了运动，飞机在天空中翱翔。类比前面的方式，你会如何研究这些物体在空间中的任意位置的速度？

学生B：将运动（速度）进行分解。教师追问：如何分解？学生B：按三个方向进行分解。教师追问：很好，这位同学是这样的观点。哪位同学想发表自己对他的观点的看法？你觉得可行吗？你有产生什么问题吗？学生C向学生B追问：为什么是三个方向？两个方向够不够？学生B：不够。学生C：为什么？教师补充：我们将其抽象成一个数学问题—

设计意图：实际生活空间中，始终存在着用任意三个不共面的向量，表示任意一个向量的必要性，在此基础上，需要体会抽象、类比、数形结合的数学思想。通过师生追问，引导学生思考发问方向，这使学生活动落在了实处，能从同伴身上学习质疑、思考的精神，发展一般性的发现问题、提出、分析、解决问题的能力。

三、 设计反思与感悟

概念教学需要渗透数学核心素养。在概念生成的过程中，提出问题、分析问题、解决问题的火花，来源于数学核心素养，来源于数学思想方法，来源于日积月累。我们可以大胆放手，让学生自己去提出一个个问题，进而研究解决，掌握空间向量基本定理的内容，达成教学目标。

概念教学需要有效追问。影响学生高层次数学思维的两个关键因素是开发需要高层次数学思维的各种数学探究任务以及试试这些任务的有效教学策略。有效追问正是一个在概念教学中的落实数学探究任务的有效教学策略。因此，在数学课堂上，教师要引导学生不断追问，自己动手，提出未解决该问题的若干小问题，不断完善外延，生成概念。

概念教学要充分发挥学生的能动性。每个学生都是未加装饰的璞玉，都是一个个鲜活的、拥有独立视角与思维能力的个体，因此在概念教学中，教师要敢于放手，不怕浪费课堂时间，不怕试错，要让学生努力尝试去提出问题、解决问题，让学生不断追问，真正落实以学生为主体、教师为主导的教学观，这样才有助于培养学生的探索精神与求知欲望，有利于学生的创新思维与理性思维的形成。