双盘直槽研磨圆柱滚子稳定自转条件分析与试验

何庆顺 何春雷 陈 光 刘伟峰 邓晓帆 任成祖

天津大学天津市装备设计与制造技术重点实验室，天津,300350

0 引言

高端轴承因其具备高精度和高可靠性[1]，被广泛应用于航空、航天、高铁、风电等众多领域[2]。高端轴承的研发应用是我国轴承产业高质量发展的短板，是已引起国家高层领导关注的制造业特别是高端装备制造业发展的“卡脖子”问题之一[3]。

圆柱滚子是圆柱滚子轴承中承受载荷的滚动体，作为承载面，其滚动面是滚子轴承中最关键、最薄弱的部分[4]，其表面质量、形状精度和尺寸一致性[5-7]是影响圆柱滚子轴承性能和可靠性的重要因素。

无心贯穿磨削是目前精加工圆柱滚子滚动面最广泛和常用的方法，其特点是无心磨床对圆柱滚子做纵向送进，一批工件连续通过磨削区，最大的优点是无需对滚子进行装夹定位，生产效率高，适用于滚子的大批量加工[8]。但是这种加工方法受机床的精度(主轴精度、进给精度等)、机床热变形以及砂轮、导轮和托板的磨损等因素的影响，各工件之间的加工条件存在细微差别，同批滚子之间的尺寸精度和一致性难以保证[9]。文献[10-11]针对目前圆柱滚子加工技术存在的加工精度低、批量一致性差问题，提出了一种行星式双平面研磨抛光方法，利用其进化加工、误差均化等特点来获得圆柱滚子外圆的高形状精度、表面质量及尺寸一致性。但是该方法受到加工原理的限制，每次加工批量很小，难以满足大批量生产的需求。

为了突破上述加工方法的局限性，文献[12-15]给出了一种双盘直槽循环研磨方法。该研磨方法中，上研磨盘工作面为平面，下研磨盘上设有一组放射状的直线沟槽，直线沟槽的槽面为下研磨盘的工作面。研磨过程中，上下研磨盘相对转动，处在上下研磨盘工作面之间的众多滚子直接相互比较，可达到滚动表面的高点材料多去除、低点材料少去除，直径较大的滚子材料多去除、直径较小的滚子材料少去除的选择性去除效果，从而提高滚动表面的形状精度和尺寸一致性。该方法通过外循环将选择性去除效应扩展至整个批次，从而实现大批量圆柱滚子滚动面的尺寸精度、形状精度、表面质量和尺寸一致性的提高。

研磨过程中，圆柱滚子绕自身轴线自转的同时沿直线沟槽做直线进给运动，自转运动是滚子滚动面材料去除的主运动，也是滚子滚动面成形的关键运动，能否稳定自转直接决定滚动面的加工质量。但是该方法中滚子自转运动的实现对上下研磨盘工作面材料的摩擦特性有着较苛刻的要求，限制了该方法的应用范围[16]，因此，如何确保滚子的自转运动能够稳定进行且不受研磨盘材料的限制，是双盘直槽循环研磨方法中的关键问题。

本文首先对双盘直槽研磨方法中圆柱滚子的受力运动情况进行分析，通过建立滚子自转运动的理论模型，得到滚子自转运动的条件；然后设计电磁研磨盘对滚子施加电磁力来确保滚子自转运动的稳定进行；最后在试验台架上对滚子的自转运动模型进行试验验证。

1 圆柱滚子自转运动条件分析

双盘直槽研磨加工原理如图1所示。研磨时，圆柱滚子在垂直于自身轴线的任意截面上的受力情况都相同，因此滚子滚动面的受力分析可以在二维平面上开展，如图2所示。图2中，v为上研磨盘与滚子接触点线速度；Ff为上研磨盘对滚子的切向摩擦力；FQ为上研磨盘对滚子的竖直载荷；Mf为Ff相对于圆心O的摩擦力矩；ω为滚子角速度；Fθi、Fθj分别为圆弧左右两侧某点对滚子的径向压力；Ffθi、Ffθj分别为圆弧左右两侧某点对滚子的切向摩擦力；Mfi、Mfj分别为圆弧左右两侧各点对滚子的摩擦合力矩。

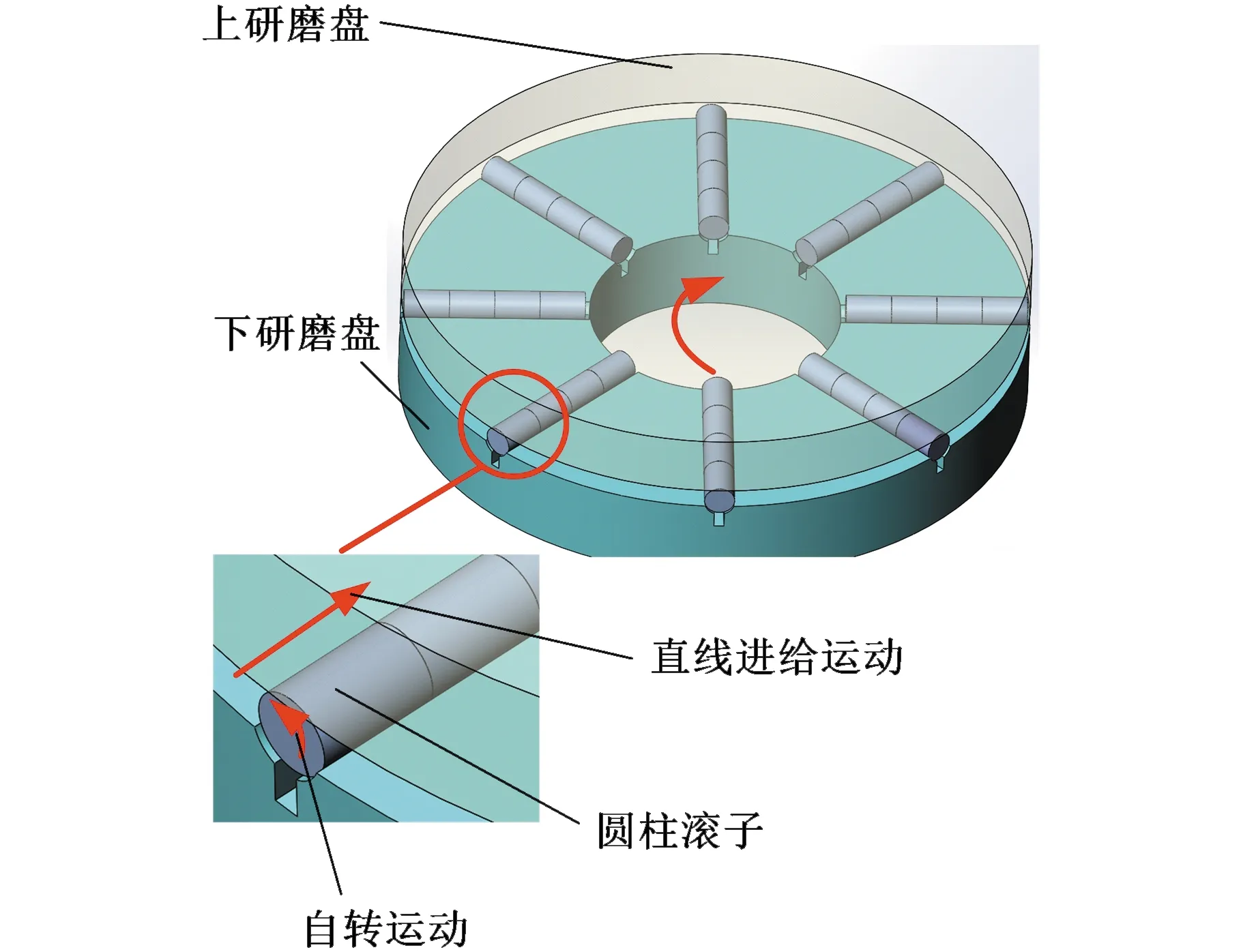
图1 双盘直槽研磨方法原理图Fig.1 Schematic diagram of double disc straight groove lapping method

图2 滚子等效二维平面受力简图Fig.2 Force diagram of roller in equivalent 2D plane

M=Mf-(Mfi+Mfj)

(1)

式中，i、j分别为直线沟槽圆弧面左右两侧各点的序号。

滚子稳定自转的条件为M>0。当滚子所受摩擦力矩满足转动条件时，滚子开始加速转动，经过时间t加速到角速度ω=v/r，之后开始稳定转动。

1.1 滚子与直线沟槽接触分析模型

为简化分析过程，根据实际研磨情况作出以下合理假设：

(1)与研磨盘尺寸相比，圆柱滚子的尺寸很小，在与研磨盘有相互作用力时，与研磨盘的变形相比，其变形可以忽略，可将圆柱滚子视为刚体。

(2)研磨加工过程中圆柱滚子半径与直线沟槽横截面的圆弧半径始终相等。

(3)与研磨压力相比，本文中使用的圆柱滚子(φ12 mm×18 mm圆柱滚子，重力G=0.16 N)自重可忽略不计。

本文所采用的竖直载荷很小(FQ≤10 N)，且滚子滚动面与直线沟槽圆弧面之间是协调接触，因此，直线沟槽的接触变形是非常微小的弹性变形(纳米级)，沟槽内部的接触应力随距接触处的距离增大而迅速减小，产生的影响只局限在接触面附近的极小范围内[17]。

Hertz接触理论广泛应用于接触力学分析，但是Hertz接触理论仅适用于接触面尺寸与物体表面的曲率半径相比很小的非协调接触情形[18]。滚子与直线沟槽的圆弧半径相等，因此属于协调接触，无法用Hertz接触理论对滚子表面的接触力进行求解。Winkler弹性接触模型常被用于求解协调接触问题[19-22]，它基于离散化的思想，将接触面模拟成无数个相互独立的“弹簧”，忽略切向力对法向力的作用，则每个“弹簧”接触力与变形量的关系为

(2)

式中，Fpi为接触区上某一点的法向接触压力；Ew为弹性层的弹性模量；Li为弹性层厚度；ui为法向弹性变形。

将Winkler弹性接触模型应用于滚子与研磨盘的接触分析模型，如图3所示。

图3 滚子只受竖直载荷时的Winkler弹性接触模型Fig.3 Winkler elastic contact model of roller with only vertical load

图3中，λ为滚子因竖直载荷产生的位移；θ为各接触点与滚子表面径向位移最大处之间的圆心角。平行四边形A1A2O2O1中，lA1A2=lO1O2=λ，当滚子的竖直位移λ很小时，A1B非常接近圆O1的切线方向，∠A1BA2≈90°，因此直线沟槽圆弧在滚子径向的位移量ui满足

ui=lA1A2cosθ=λcosθ

(3)

将式(3)代入式(2)，可得到滚子表面任意点处受到的径向压力

(4)

由前面的假设和分析，对于常用的研磨盘材料，如中碳钢、铸铁、聚四氟乙烯等，Ew、Li皆可视为常数。当载荷确定时，各接触点上的接触力满足余弦分布规律：

Fp(θ)=Fp0cosθ

(5)

式中，Fp0为假设滚子表面径向位移最大处受到的接触压力。

1.2 滚子稳定自转条件分析

图4中，由于上研磨盘摩擦力以及直线沟槽对滚子的摩擦力的作用，滚子表面径向位移最大处的径向相对竖直方向的圆心角为δ+β，对滚子进行如下受力分析。

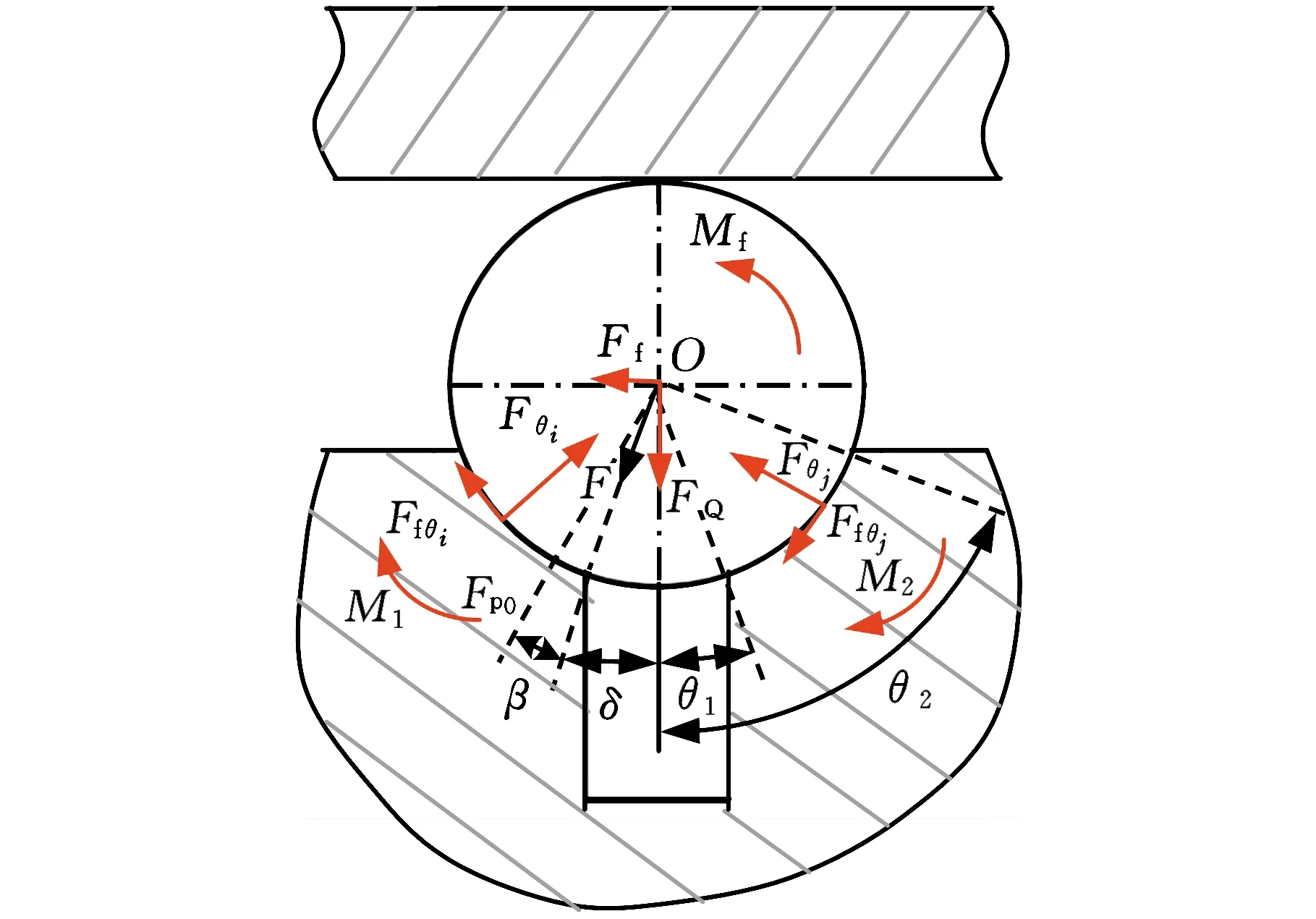
图4 滚子详细受力分析Fig.4 Detailed force analysis of roller

竖直方向：

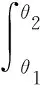
(6)

水平方向：

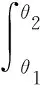
(7)

稳定自转条件：

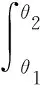
(8)

其中

Mf=Ffr

(9)

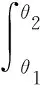
(10)

(11)

式中，μ1为滚子与上研磨盘的摩擦因数；μ2为滚子与直线沟槽的摩擦因数；l为圆柱滚子长度。

由于磨料和研磨液的作用，滚子与上下研磨盘之间为复杂的三体研磨，μ1、μ2无法按照经验值选取。邓晓帆等[23]设计销盘摩擦磨损试验测定了研磨状态下GCr15轴承钢与常用研具材料的滑动摩擦因数，如表1所示，本文中所用摩擦因数都是基于该文献中的实测结果。试验中，研磨液的成分(质量分数)为：10%的白刚玉磨粒，20%的丙三醇，70%的纯水。其中磨粒的平均粒度为W40，试验载荷为10 N，环境温度为23 ℃。

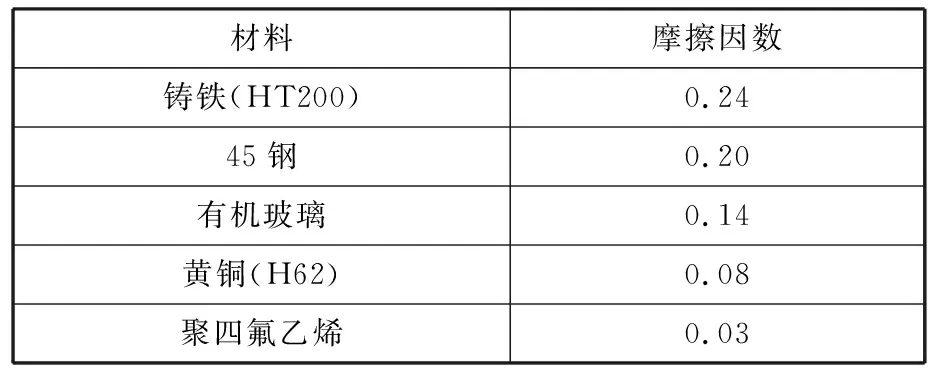
表1 GCr15轴承钢与研具材料的滑动摩擦因数[23]Tab.1 Coefficient of sliding friction between GCr15 bearing steel and lapping tool material[23]

通过求解式(6)～式(8)可得到特定参数条件下满足稳定自转条件的驱动力矩的临界值：

Mf0=Mfi+Mfj

(12)

定义驱动力矩Mf与临界值Mf0的差值为ΔMf，ΔMf>0则总摩擦力矩M>0。以上研磨盘材料为有机玻璃、下盘材料分别为聚四氟乙烯和45钢为例，ΔMf与θ1、θ2之间的关系如图5所示。

(a)μ1=0.14，μ2=0.03

(b)μ1=0.14，μ2=0.20图5 ΔMf随θ1、θ2的变化Fig.5 Changes of ΔMf with θ1、θ2

由式(6)～式(8)和图5可以看出，ΔMf随着μ1的增大而增大，随着μ2、θ1、θ2的增大而减小。图5b中ΔMf在θ1、θ2的变化范围内一直小于0，表示当上研磨盘材料为有机玻璃、下研磨盘材料为45钢时，在图中的θ1、θ2取值范围内滚子始终无法稳定自转。为了使其满足稳定自转条件，通过在滚子与上研磨盘之间施加电磁力，人为地增大滚子与上盘之间的接触力，实现圆柱滚子的稳定自转，受力分析如图6所示。图中，FC为上研磨盘对滚子的电磁力，F′C为由电磁力引起的上研磨盘对滚子的压力，F′C=FC。

图6 滚子在电磁力作用下与上研磨盘的作用力Fig.6 Force between roller and upper lapping disc under electromagnetic force

与无电磁力相比，滚子与上研磨盘之间的接触力由FQ变为FQ+FC，从而增大了摩擦力Ff和驱动力矩Mf，即

Ff=μ1(FQ+FC)

(13)

Mf=Ffr=μ1(FQ+FC)r

(14)

当下研磨盘材料为易于被磁化的金属材料时，下研磨盘直线沟槽的接触面也会被磁化，会增大滚子与直线沟槽的接触力，增大滚子所受的摩擦阻力矩。但是由于下研磨盘与上研磨盘(电磁研磨盘)之间有一定距离，直线沟槽的磁化是非常轻微的，分析时可忽略，因此只要施加适当的电磁力FC，即可将原来不满足稳定自转条件的情况转变为满足稳定自转条件的情况，实现圆柱滚子的稳定自转。

2 电磁研磨盘结构设计与仿真

本文主要研究研磨盘内滚子的稳定自转条件，不涉及大批量循环。在下盘设置4条直线沟槽，每个沟槽中有3个滚子。为了使滚子在上盘的径向位置固定，在上研磨盘的盘面上设置3个环形槽，如图7所示。

图7 研磨盘面结构Fig.7 Structure of lapping disc surface

电磁吸盘的设计要求为：①能够提供足够大的电磁力以驱动滚子自转；②研磨区域的每个滚子所受的电磁力尽可能一致。

2.1 电磁研磨盘结构设计

磁力吸盘的设计方法有磁路法、有限元法和解析法等[24]。磁路法利用磁路与电路之间的相似性，用类似电路的方程来求解磁路，求解简单，计算速度快，但精度较低。有限元法能够考虑磁性材料的非线性、漏磁效应，计算更为精确。因此，本文首先用磁路法确定电磁研磨盘的磁路结构，再用有限元仿真软件对其进行仿真验证和优化，根据设计要求确定磁路中各部分的具体尺寸。

电磁研磨盘的结构和工作原理如图8所示。当有直流电通过线圈时，线圈附近的磁轭将会产生磁势，在磁势的作用下磁通将沿着磁轭和滚子闭合流通[25]，被磁化的滚子和研磨盘面板之间将会产生电磁吸力。隔磁环的材料为铜，起到阻断磁轭中磁通的作用，从而使磁通更多地通过滚子，增大滚子受到的电磁力。

1.圆柱滚子 2.磁轭 3.隔磁环 4.虚拟磁力线 5.线圈 6.环氧树脂填充物图8 电磁研磨盘工作原理Fig.8 Principle of electromagnetic lapping disc

在磁路分析中，由于滚子尺寸相对研磨盘来说较小，且每批只加工12个滚子，对研磨盘整体磁场分布影响很小，因此在磁路分析中将滚子忽略，只研究研磨盘的磁场。

当忽略漏磁效应时，磁轭中垂直于磁通方向的各截面的磁通量相等。磁轭中垂直于磁通方向各个截面处的磁感应强度为

(15)

式中，I为线圈中的电流；N为线圈匝数；Φ为磁通量；Rm为磁轭的磁阻；S为导磁体在垂直于磁通量方向上的截面积。

由式(15)可知，当磁动势NI和磁阻Rm确定时，B与S成反比。磁吸力的经验公式为

(16)

式中，Φ0为气隙磁通量；B0为气隙磁感应强度；μ0为气隙磁导率，μ0=4π×10-7H/m；S0为气隙磁路截面积。

式(16)中，μ0和S0是确定值，滚子所受的电磁力只与气隙的磁感应强度B0相关。气隙中的磁感应强度分布较复杂，很难求出，但是只要满足3个环形沟槽中磁感应强度分布相同，则气隙中的磁感应强度相同，滚子所受的电磁力也相等。

为达到上述目的，应使每个隔磁环上方磁轭的磁感应强度相等，如图9所示，图中，R1、R2、R3为3个环形槽中心在盘面上的半径，R1、R2、R3处磁轭的截面积为

Si=Cihi=2πRihii=1,2,3

(17)

式中，Ci为上研磨盘面上半径为Ri处圆的周长；hi为环形槽处的磁轭厚度。

图9 电磁研磨盘面结构Fig.9 Structure of electromagnetic lapping disc surface

磁感应强度的关系如下：

B1∶B2∶B3=(h3R3)∶(h2R2)∶(h1R1)

(18)

因此，每个隔磁环上方的磁感应强度与各自的磁轭半径Ri成反比，与磁轭厚度hi成反比，只要满足h1R1=h2R2=h3R3，即可实现3个环形槽与滚子的接触面上的磁场分布相同，达到每个滚子所受电磁力一致的目标。

2.2 电磁场仿真分析

为了确定磁轭各部分具体尺寸，通过ANSYS Maxwell电磁有限元仿真软件对电磁研磨盘进行仿真分析。电磁研磨盘的二维电磁场仿真模型如图10所示，为了满足h1∶h2∶h3=R3∶R2∶R1，相比于图10a，图10b中隔磁环背面也有相同宽度、不同深度的环形槽。图10的仿真结果表明，图10b的3个环形槽磁感应强度分布比图10a中所示的磁感应强度分布更加均匀。

(a)磁轭初始磁感应强度分布

(b)结构修改之后的磁感应强度分布图10 ANSYS Maxwell二维磁场分布Fig.10 ANSYS Maxwell 2D magnetic field distribution

在三维电磁场仿真模型中对滚子所受到的电磁力进行计算。磁轭的材料既要有良好的导磁性能，也要具有较强的耐磨性，因此磁轭的材料选为综合性能较优的10钢。经过对磁轭各位置的不同尺寸组合进行仿真，使磁轭的结构既能使滚子受到较大的电磁力，又能满足结构的强度要求，最终确定的结构参数如图11和表2所示。图中T1、T2、T3为研磨盘基体磁轭厚度。

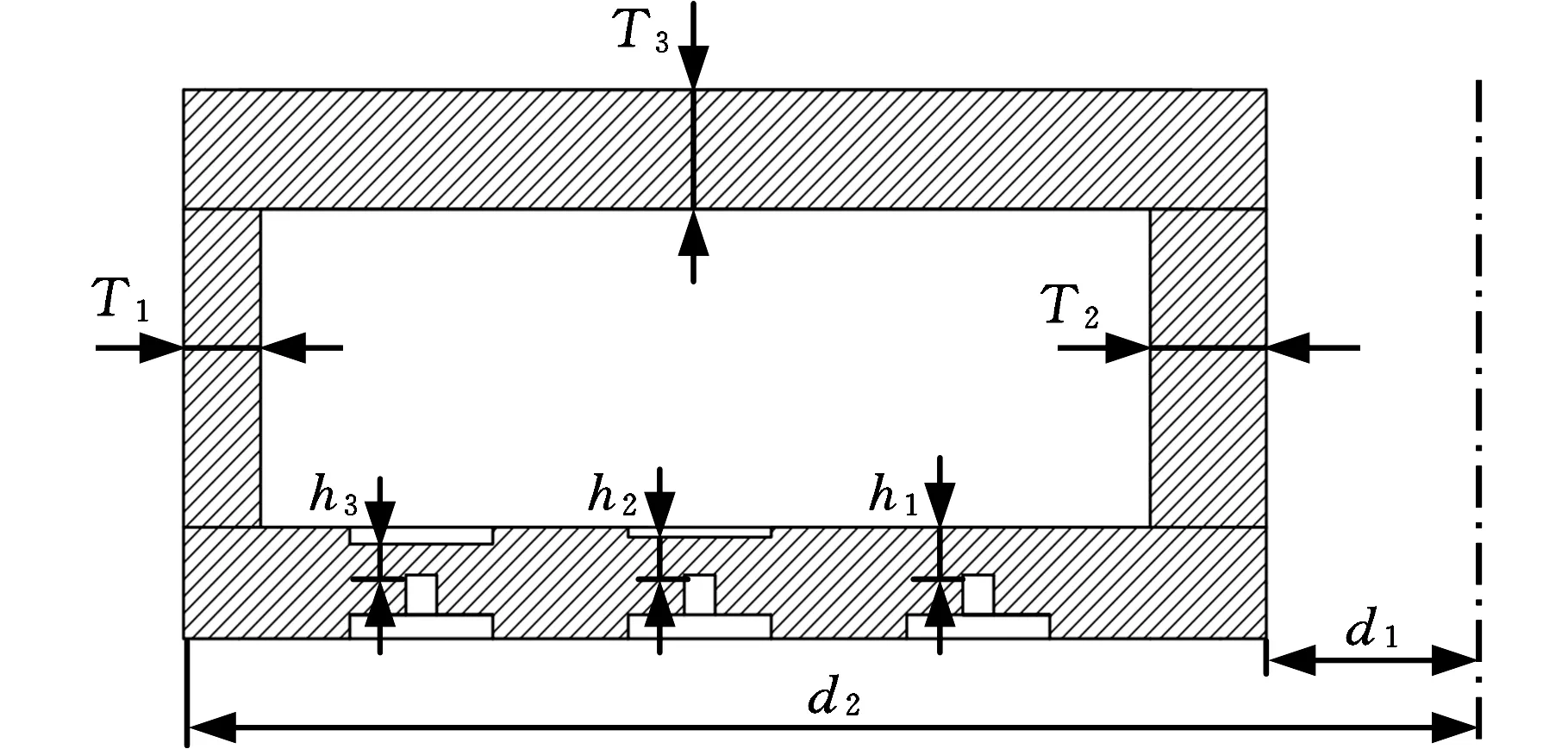
图11 磁轭尺寸示意图Fig.11 Schematic diagram of dimensions of magnetic yoke

表2 磁轭结构尺寸参数Tab.2 Dimension parameters of magnetic yoke mm

图12 滚子电磁力仿真结果Fig.12 Simulation results of roller electromagnetic force

在表2所示结构尺寸条件下，滚子受到的电磁力仿真计算结果如图12所示。由图12可知，在本研究涉及的电磁力范围内，滚子所受的电磁力与线圈激励近似成正比，且内圈、中圈和外圈环形槽中的滚子所受的电磁力基本相等，满足设计要求。

3 试验验证

本文试验是在自制的双盘直槽试验台架(图13)上进行的，其原理图见图14。工作时电磁研磨盘(上盘)固定，下研磨盘转动，设置凸轮/弹簧恢复机构，在下研磨盘转动的同时推动直线沟槽在下研磨盘的导轨中往复运动，以模拟滚子沿着下研磨盘的直线沟槽做直线进给运动。

图13 试验台架实物图Fig.13 Picture of experimental platform

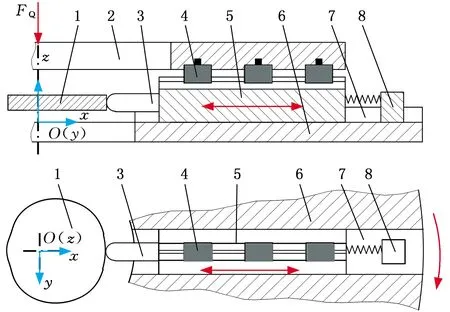
1.凸轮(固定) 2.上研磨盘 3.研磨条导柱 4.圆柱滚子 5.研磨条 6.研磨条底座 7.滑槽 8.往复弹簧 9.弹簧座图14 试验台架原理图Fig.14 Schematic diagram of experimental platform

3.1 电磁研磨盘电磁力验证

使用弹簧测力计对电磁研磨盘内、中、外3个环形槽中放置的滚子所受的电磁力进行测量，测量方法见图15。将电磁研磨盘面朝上，在滚子上粘贴挂钩，使用弹簧测力计沿竖直向上的方向匀速、缓慢地拉滚子，当滚子脱离电磁研磨盘面时，弹簧测力计的示数达到最大，记录该最大值，即为滚子所受电磁力。结果如图16所示，3个环形槽中滚子受到的电磁力基本相同，其差距在可接受范围内。实测电磁力比仿真所得电磁力(图12)小，误差平均值为9.76%。分析误差产生的原因，可能是由于仿真软件中的磁轭和滚子材料的导磁性能为理想状态，而实际材料受到杂质、热处理方式等因素影响，导磁性能比理想状态下低，导致滚子实际电磁力比仿真结果低。

图15 电磁力测量原理Fig.15 Measurement principle of electromagnetic force

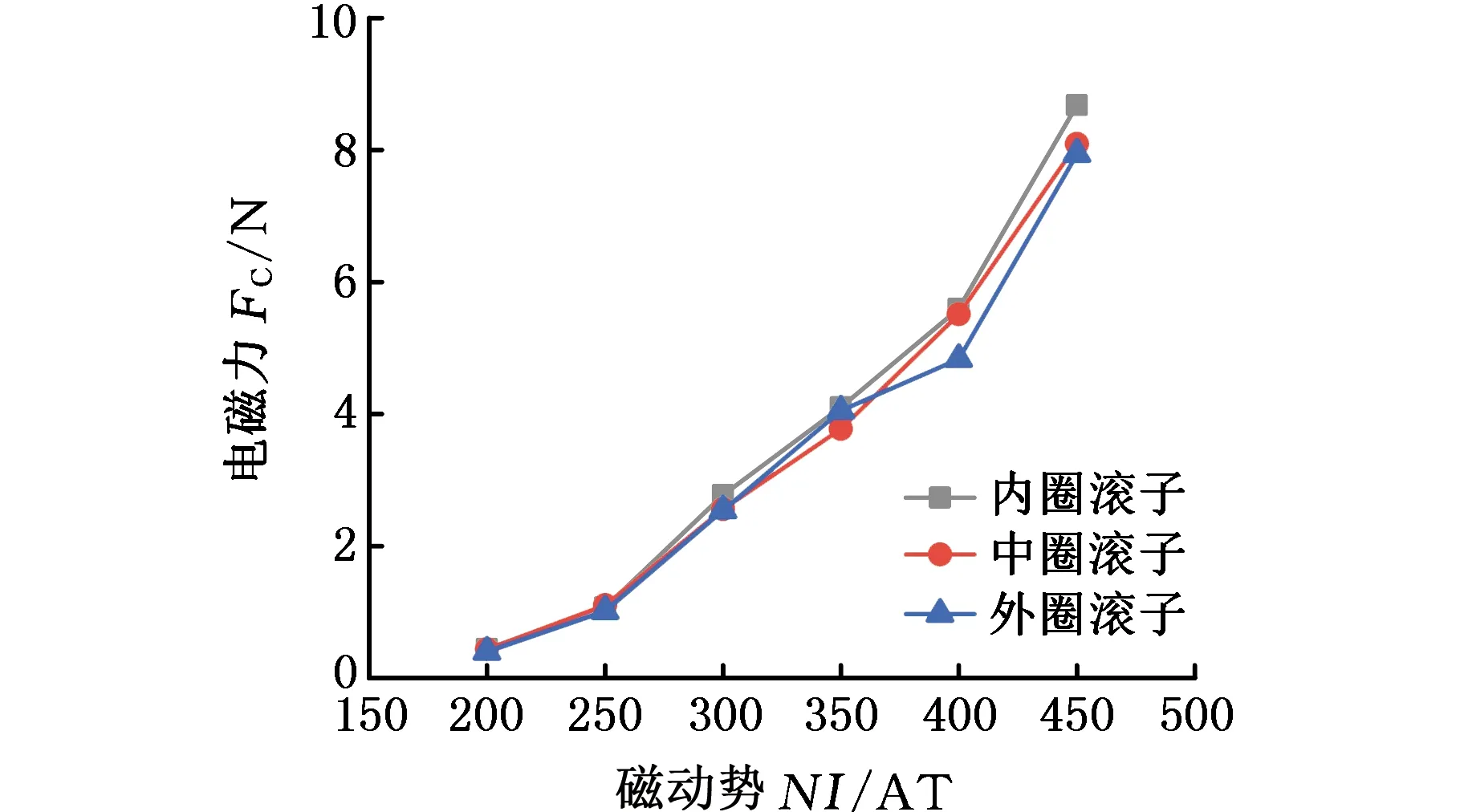
图16 滚子电磁力实测结果Fig.16 Measurement results of roller electromagnetic force

3.2 自转运动模型的验证

图17 直线沟槽结构Fig.17 Structure of straight groove

由前述分析可知，在上研磨盘摩擦因数μ1(取轴承钢与10钢和黄铜的综合摩擦因数0.17)确定的条件下，圆柱滚子转动条件与μ2、θ1和θ2有关。因此，本文设置3种不同的直线沟槽，结构形式如图17所示，在表1所示的参数条件下，分别测量实现圆柱滚子稳定自转的最小电磁力，并与理论模型的计算结果进行比较，如表3所示。对于试验组1，实测最小电磁力与理论计算结果相同，滚子不需要附加电磁力即可实现稳定自转。试验组2和试验组3需要附加电磁力才能实现稳定自转，实测最小电磁力分别为4.2 N和7.0 N。试验结果与理论计算结果的误差分别为13.5%和11.1%。误差的来源可能有以下三种：

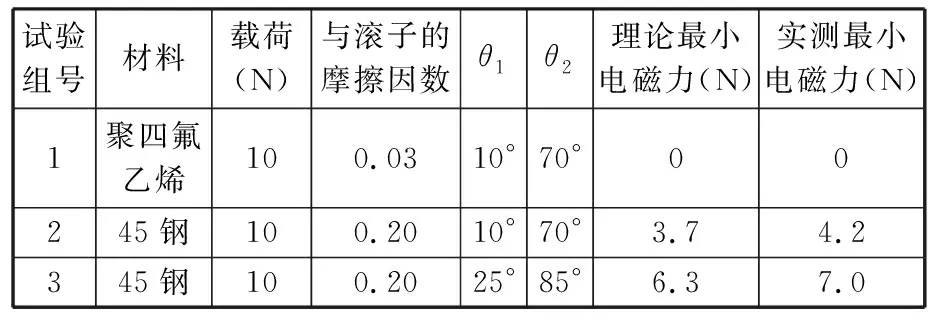
表3 直线沟槽参数与最小电磁力试验结果Tab.3 Parameters of straight groove and experimental results of smallest electromagnetic force

(1)使用Winkler弹性基础模型计算滚子与直线沟槽接触力时，为了简化计算过程，假设切向力与法向力相互独立，实际上切向力对法向力有一定的影响[26]。

(2)电磁吸盘对45钢材质的直线沟槽会造成轻微磁化，从而使滚子和直线沟槽之间也有电磁力的作用，增大了滚子和直线沟槽之间的接触力。

(3)圆柱滚子的重力对直线沟槽也有一定的压力作用，忽略了重力导致上述压力在分析过程中缺失。

以上原因可能造成摩擦阻力矩计算值偏小，从而导致表3中理论最小电磁力偏小，但是试验结果验证了滚子稳定自转所需最小电磁力随着μ2、θ1和θ2的增大而增大的规律。

为了进一步验证滚子的转速模型，本文在滚子端面上刻出标记线，使用帧率240 s-1的摄像机对滚子的转动状态进行高速拍摄，滚子的自转角Δα的定义如图18a所示。通过视频的图像信息可以得到滚子转动Δα所用的时间t，因此滚子的实际转速ω=Δα/t。

图18b中，理论转速6.22 r/s是假设滚子母线中心点与上盘发生纯滚动、接触点线速度相同而计算的。可以看出，当滚子稳定自转时，实际转速接近理论条件下的转速。

3.3 研磨试验

(a)滚子转速测量方法

(b)滚子转速与电磁力关系图18 滚子转速测量Fig.18 Measurement of roller rotating speed

使用3.2节中的3种直线沟槽分别进行研磨试验。每隔10 min取出全部12个滚子，使用Talyrond131圆度仪测量滚子圆度，然后随机打乱滚子位置继续研磨。试验条件见表4。在研磨液的润滑条件下，磨料粒度对摩擦因数的影响较小，为了得到更好的研磨效果，使用平均粒度W1的Al2O3磨料，在试验中仍能观测到滚子稳定自转。滚子的平均圆度变化和平均累计直径去除量如图19所示。

表4 研磨试验参数Tab.4 Experimental parameters of lapping

由图19可知，3组试验中滚子的平均圆度误差随着研磨时间有明显减小，图19a中滚子平均圆度误差由初始值2.60 μm减小到0.85 μm，图19b中滚子平均圆度误差由初始值2.55 μm减小到0.63 μm，图19c中滚子平均圆度误差由初始值2.60 μm减小到0.68 μm；其中试验组2最后的滚子平均圆度误差最小，试验组3次之，试验组1平均圆度误差最大。此外，试验组3平均累计直径去除量最高，为6.5 μm，试验组2为6.1 μm，试验组1为4.2 μm，且随着加工时间的延长，材料去除量呈近似线性增大。上述结果表明，在采用电磁研磨盘的条件下，只需要较小的材料去除量就可以使滚子的圆度误差得到明显减小，并且适当增大滚子-研磨盘的摩擦因数，可以提高单位时间的滚子材料去除量，从而更快地减小滚子的圆度误差。

(a)试验组1

(b)试验组2

(c)试验组3图19 滚子平均圆度误差和平均累计直径去除量Fig.19 Average roundness error and average accumulate diameter removal of roller

如图20所示，经过60 min研磨后，滚子滚动面截面轮廓从原来的五棱圆转变成较标准的圆，说明在整个研磨过程中滚子都保持着良好的自转运动，并且遵循高点多去除、低点少去除的选择性去除规律。

(a)初始截面轮廓(b)60 mim研磨后的截面轮廓图20 滚子滚动面截面轮廓Fig.20 Section profile of roller rolling surface

4 结论

(1)本文根据滚子在研磨盘中的受力状态，计算了滚子实现稳定自转运动的理论条件。计算结果表明，驱动力矩与滚子实现自转所需的临界驱动力矩的差值随着滚子和上研磨盘摩擦因数μ1的增大而增大，随着滚子和下研磨盘摩擦因数μ2、直线沟槽圆弧起始圆心角θ1、终点圆心角θ2的增大而减小。

(2)对于滚子无法稳定自转的情况，采用电磁研磨盘引入电磁力，可以增大驱动圆柱滚子自转的摩擦力矩，改善滚子的自转条件。设计了电磁研磨盘，仿真和试验结果显示电磁吸盘3个环形槽中的滚子所受电磁力基本一致。

(3)通过滚子自转试验得到了3种直线沟槽中滚子实现稳定自转所需要的最小电磁力，试验结果与理论模型计算结果吻合。研磨试验结果显示，在材料去除量较小的情况下，滚子圆度误差得到明显减小，且适当增大滚子-研磨盘的摩擦因数，可以有效提高滚子材料去除量，更快地减小滚子圆度误差，且双盘直槽研磨方法具有明显的高点多去除、低点少去除的选择性去除效果。