预防维护下装配线平衡的多目标重启变邻域搜索算法
赵联鹏 唐秋华 张子凯 蒙 凯
1.武汉科技大学冶金装备及其控制教育部重点实验室,武汉,4300812.武汉科技大学机械传动与制造工程湖北省重点实验室,武汉,430081
0 引言
装配流水线常用于汽车、电器等产品的大批量生产,是制造型企业最基本的生产单元。装配线的平衡程度直接影响制造系统的效率,关乎产品质量以及生产成本,因此使装配线达到平衡状态至关重要。装配线平衡问题(assembly line balancing problem, ALBP)就是将所有基本工作单元分派到各个工位,以使每个工位在节拍(相邻两产品通过装配线尾端的间隔时间)内都处于繁忙状态。该问题自被提出以来就受到学者广泛关注,BOYSEN等[1]根据求解目标将其划分为四类,并衍生出一系列变体问题及相关理论,其求解方法多样,可分为精确算法[2]、启发式算法[3]以及元启发式算法[4]。
由于设备损耗、不确定性因素的存在,在实际生产时机器会出现故障,又因为装配线生产过程具有连续特征,故障一旦出现便会导致生产过程中断,故需要对机器进行维护。设备维护通常分为纠正性维护(corrective maintenance, CM)和预防性维护(preventive maintenance, PM)。前者在设备发生故障后进行维修,属于事后维护;后者利用机器诊断、定期检查等技术对设备状态进行监测,并有针对性地安排维修,该方法可以将机器故障事先排除,提高设备的可靠性,减少或避免停机损失[5]。
预防维护现已成为制造型企业普遍采用的设备维护方式。预防维护与车间调度的相互影响很大,集成预防维护和车间调度的研究近年来也大幅度增加。ALIREZA等[6]将预防维护与柔性流水车间调度进行集成优化,提出了融合遗传算法与模拟退火算法的元启发式算法,以最小化最大完工时间。WANG等[7-8]提出多目标禁忌搜索以及四种启发式算法,分别求解预防维护与两阶段混合流水车间、双机流水车间集成调度问题。同样,在已知预防维护计划前提下,也应考虑基于预防维护情形的装配线平衡,以便在设备维护时迅速做出生产调整。面向该问题,蒙凯等[9-10]建立多目标优化模型,并提出了改进多目标灰狼算法与改进鲸群优化算法两种群智能算法。ZHANG等[11]针对考虑预防维护的U型装配线平衡问题,提出改进多目标JAYA算法。总体来说,针对预防维护下的装配线平衡研究相对较少,并且求解方法主要集中在群智能算法的改进。仍然有必要对预防维护下的装配线平衡问题进行深入研究,特别是面向问题独有特征的分析,同时应拓展如局部搜索等求解方法,以结合问题本质特征,快速有效求解问题。
为此,本文提出了一种多目标重启变邻域搜索(multi-objective restart variable neighborhood search, MORVNS)算法,探索面向预防维护下装配线平衡问题属性的邻域结构特征与Pareto前沿推进方法,并且将其与基本变邻域搜索算法、改进多目标灰狼算法以及另外四种经典算法进行比较,以评估所提算法的有效性和优越性。
1 问题描述
1.1 预防维护下的装配线平衡
相比正常工作,预防维护会使得工作工位减少、生产节拍增加以及工序调整,这时需根据工序间的优先关系确定操作序列,同时将相应工序重新分配到不同的工位,并保证正常工作和预防维护两种情形下的生产效率。如图1所示,某案例具有12道工序和4个工位,已知各工序操作时间及其优先关系。由于工位2需要进行预防维护,则工序[5 3 6 9]需要进行调整。
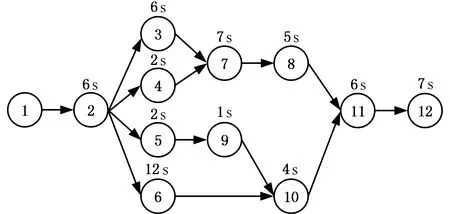
(a)各工序优先关系
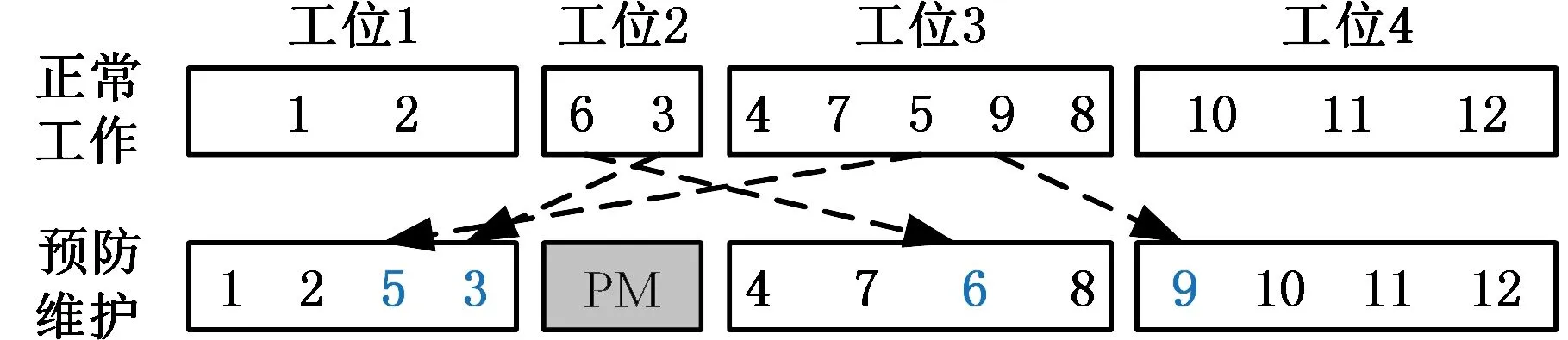
(b)工序安排图1 工序优先关系及安排Fig.1 Process priority relationship and arrangement
由此可以看出,正常生产和预防维护情形下的任务分配既具有一定的相同性,同时又具有极强的差异性。其中,相同性体现在:不同情形下的工序分配都必须满足优先关系;各工位时间不能大于当前情形下的生产节拍。差异性主要体现在以下三个方面:
(1)预防维护情形下,至少有一个工位被维护,被维护工位没有生产能力,其他工位能够参与生产。考虑到工位维护会改变生产状态,所以会导致一定时间的生产中断,为缩短该调整时间,每次维护应暂停尽可能少的工位。
(2)预防维护下参与生产的工位减少,意味着该情形下的生产节拍不会小于正常工作时的生产节拍。
(3)预防维护工位的工序需调整到其他工位,而且其他工位上的工序也可能会被调整,以达到负载均衡的目的。因此工序调整数应尽量少,以减少调整时间并更好地保持生产连续性。
1.2 多目标优化模型
预防维护下的装配线平衡优化正常工作、维护情形下的节拍与工序调整三个目标,基于此构建多目标优化模型,并做出以下假设:
(1)已知各个工序的操作时间与优先关系;
(2)各道工序必须并且只能够被加工一次;
(3)在每一个工位上都能够加工所有工序;
(4)装配线是生产单一产品的单边直线型;
(5)不考虑工序准备时间与工件移动时间;
(6)每次计划必须且只能够维护一个工位。
模型中,n为工序数;m为工位数;I是工序集合,I={1,2,…,n},i,k∈I;J是工位集合,J={1,2, …,m},j,l∈J,l为需要维护的工位序号;S是工作情形集合,S={0, 1,…,m},ω∈S,当ω=0时为正常工作的情形,ω=l时为对第l号工位预防维护的情形;Pn×n为优先关系矩阵,若工序i为工序k的直接前序则Pik=1,否则Pik=0;ti为第i道工序的加工时间;Cω是ω情形下的生产节拍;Aω为正常工作转换到ω情形下的工序调整数量,当ω=0时Aω=0;Xijω是决策变量,表示在ω情形下,若工序i分配到工位j上则Xijω=1,否则Xijω=0。
基于上述定义,该问题多目标优化模型的目标函数可以表示为
z1=minCω=0
(1)
z2=minCω=l
(2)
z3=minAω=l
(3)
式(1)与式(2)分别表示最小化正常工作以及预防维护情形下的生产节拍;式(3)表示最小化由正常工作切换到某种预防维护情形时产生的工序调整数量,其计算依据下式:
(4)
式(4)通过将预防维护与正常工作情形下每个工位上的工序分配相比较,来计算该预防维护情形下的工序调整总量,以便进行生产准备。
多目标优化模型的约束条件可以表示为
(5)
(6)
(7)
(8)
(9)
式(5)为工序分配约束,表示每道工序都必须分配到一个工位并且只能分配一次;式(6)为工序优先关系约束,表示只有当某工序的所有紧前工序全部完成后才能对其进行分配;式(7)与式(8)为工位分配约束,表示工位不被维护时应至少被分配一道工序,进行维护的工位不应该被分配任何一道工序,因此被维护工位上的总操作时间为零;式(9)为节拍约束,表示在ω情形下任何一个工位上的总操作时间都不能大于生产节拍。
2 多目标重启变邻域搜索算法
变邻域搜索算法(VNS)[12]是一种经典的局部搜索算法,因其结构简单、易于实现且参数较少等优点,自提出以来就被广泛应用于生产调度、路径规划等组合优化问题,它通过对多邻域进行特定形式的搜索来找到问题的满意解。装配线平衡问题是典型的NP-hard问题,当问题规模较大时需要运用近似算法对其进行求解,在该问题研究领域,变邻域搜索算法已被应用于优化双边装配线平衡问题[13-14]中工人数量、线长以及生产节拍。
基本变邻域搜索算法通过设计扰动算子来避免陷入局部最优。本文所提算法设计重启算子以替代扰动算子作为跳出局部最优的手段,并对多种邻域结构的选择、组合与搜索策略进行研究。
2.1 初始化与解码
2.1.1初始解的生成
预防维护下装配线平衡问题的可行解包括正常工作、设备维护情形下的工序安排以及工序调整三部分,解的表达采用满足优先关系的实数编码[9]。在局部搜索算法中,初始解通常由随机或启发式方法获得,从一个性能较优的初始解出发能够更快找到满意解。
考虑多目标和装配线平衡问题的特性,本文所研究问题的初始解利用启发式规则与随机编码相结合的方式生成。首先按照最短操作时间(shortest processing time, SPT)规则[15]、最长操作时间(longest processing time, LPT)规则[16]、优先位置权重(ranked positional weight, RPW)规则[17],分别混合最短与最长操作时间和优先位置权重规则随机编码生成6种操作排序方案,由此得到36个不同的待选初始解。然后,利用“擂台赛法则”[18]依据它们的目标函数值进行非支配排序,找出初始非支配解集,并计算解集中各解与其他解之间的距离,最终选出距离之和最大的解作为初始解。
2.1.2固定工位下的动态迭代解码
在求解预防维护下装配线平衡问题中的不同工作情形下的生产节拍时,其本质是求解第二类装配线平衡问题,即在给定工位数时最小化生产节拍。当操作序列确定后需要将各工序分配到各工位并获得该序列下的最小生产节拍。由于每种生产情形下工位数目固定,又因同一序列的分配方案有多种,故不能采用增加工位的方式进行解码,所以采用固定工位下的动态迭代解码。基于某一情形下的工序操作序列,具体解码步骤如下。
(1)依据下式计算该操作序列下的理论最小生产节拍:
(10)
并令当前节拍C=CE。
(2)按照当前节拍C将该序列中的操作依次分配到各工位,直至分配到第(m-1)号工位满足当前节拍要求,然后将剩余操作全部依次分配给第m号工位。
(3)计算此时每个工位上的总操作时间Tj与T′j,后者的计算公式如下:
T′j=Tj+t1(j+1)
(11)
其中,t1(j+1)表示此时第(j+1)个工位上的第一道工序的操作时间。
(4)令C′=maxTj,C″=minT′j,若C′≤T″,那么C″就是该操作序列下的最优生产节拍,此时的分配方案也为该操作序列下的最佳分配方案;若C′>C″,那么,令当前节拍C=C″,并重复步骤(2)~步骤(4)。
针对每种情形,固定待维护工位和可工作工位,运行上述解码,可获得目标值(C0,Al,Cl)。其中,C0为正常工作情形下的生产节拍;Cl为对l号工位进行维护的情形下的生产节拍;Al为两种情形切换时的工序调整数量。
2.2 接收准则
新解的接收准则是:若该解能支配当前Pareto前沿解集中的某些解,或者与其中所有解互不支配,那么就将该解放入前沿解集并删除被其支配的所有解,否则丢弃该解;在新解与当前非支配解集中的所有解互不支配时,则将其保留在前沿解集中,但不认为前沿解集获得实质性推进;只有当前Pareto前沿解集中全部或者部分解被新解支配时才认为其发生实质性推进。
2.3 变邻域搜索算子
在对多邻域进行搜索时,若邻域结构数量太多则会增加计算的时间成本,反之将会导致对解空间探索不完全,最终遗失满意解。因此,在进行算法设计时必须考虑以下三点内容[12]:
(1)设计恰当数量并且针对问题属性的邻域结构;
(2)确定所采用的多种邻域结构的排列组合形式;
(3)采用面向问题属性寻优能力最好的搜索策略。
在本文所提算法中,对上述内容进行深入研究,并最终使算法展现出相对较好的性能。
2.3.1邻域结构的选择
针对装配线平衡问题,现已有发展成熟且性能良好的邻域结构,如互换算子、后插算子以及前插算子。在搜索阶段,通常为了追求运行速度而忽略邻域解的可行性,一般采取修复机制使不可行解转换为可行解,这种设计方法不仅降低了产生可行解的概率又增加了计算复杂度。修复机制如同设备管理中的纠正性维护,本文在设计邻域算子时运用预防维护思想,选取互换、后插与前插三种邻域结构,并根据工序优先关系设计一次互换与多次互换、一次后插与多次后插、一次前插与多次前插六个算子以生成可行邻域解,并且避免各算子邻域空间出现重叠现象,消除重复操作带来的时间损失。
同时,本文设计了一种新型邻域结构,称为重排式邻域算子。已知某一操作序列,随机选择其中任意两个位置,分别以近前端、近后端为起止点截取子序列,并根据子序列中各操作之间的优先关系形成部分优先关系矩阵,基于此对子序列进行重新排列得到新序列,如图2所示。该例中起点为3、终点为9,初始子序列包含操作为[6 3 4 7 8 5 9],根据优先关系重新排列之后得到新的子序列[4 5 9 3 6 7 8],对应地,由初始序列[1 2 6 3 4 7 8 5 9 10 11 12]得到新的可行邻域解序列[1 2 4 5 9 3 6 7 8 10 11 12]。
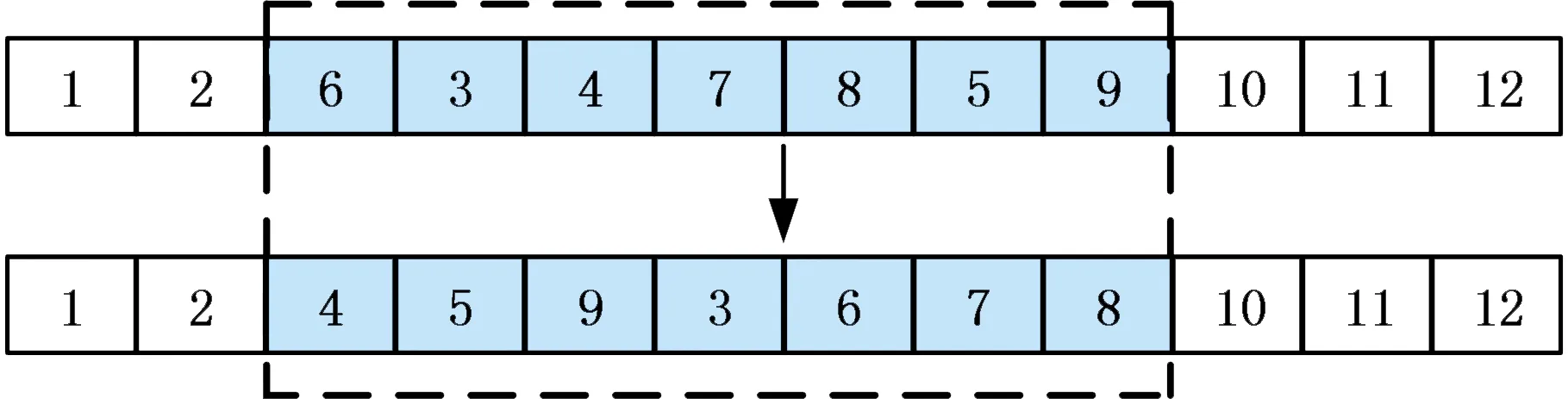
图2 重排式邻域算子实例Fig.2 Examples of rearranged neighborhood operators
2.3.2邻域结构的排序
所提算法采用四类七个邻域结构,除重排式邻域结构之外,实现了互换、后插与前插算子的邻域解空间完全没有交叉部分。而重排式邻域结构随机性大,其邻域解空间与其他三类算子的解空间有部分重叠,在其余算子探索不到的解空间,该结构起一定的补足作用。
大量实验证明,根据工序优先关系实现的四类邻域结构性能由优到劣依次为重排、互换、后插和前插,在邻域搜索阶段多种邻域结构按此顺序进行排列,以保证尽快找到满意解。
2.3.3搜索策略的选择
多邻域结构的搜索方式通常有三种,分别是每次迭代随机选择一种邻域结构进行探索的随机邻域搜索(stochastic neighborhood search, SNS)策略、交替进行的变邻域搜索策略和对多种邻域结构全部探索的全局邻域搜索(global neighborhood search, GNS)策略。
面向预防维护下装配线平衡问题,邻域搜索策略采用交替搜索。理论上,假设选取K种不同的邻域结构,在每次迭代时随机搜索策略的计算复杂度为1,该策略时间成本最低;全局邻域搜索策略的计算复杂度为K,时间成本最高;而采用交替搜索策略时计算复杂度在区间[1,K]内,时间成本也在其他两种策略之间。采用三种搜索策略展现出的性能也将通过实验算例进行验证说明。
当邻域结构选择、组合以及搜索策略确定之后,随即实现重启前的变邻域搜索阶段(variable neighborhood search before restart, VNSBR),使它在算法中承担重启前的探索工作,并依据接收准则对新解进行判断。伪代码如下所示。
算法1VNSBR
1: Input:Ω,Nh(h=1, 2,…,K),POS
2: Begin:
3:d=0;
4: Forh=1 toKdo
5:Ω′=Nh(Ω);
6: If ∃π∈POS:Ω′πthen
7:POS←POSπ∪Ω′;
8:Ω←Ω′ ∧d=0;
9: break
10: Else If ∀π∈POS:πΩ′then
11:d←d+1;
12: Else
13:POS←POS∪Ω′;
14:d←d+1;
15: End If
16: End For
17: Output:Ω,POS,d
算法1中,Ω为被探索解;Ω′是邻域解;Nh表示第h种邻域结构;POS为当前Pareto前沿解集;POSπ表示解π在POS中的相对补集,是由POS中所有不同于π的解组成的集合;d用来记录前沿解集连续未发生实质性推进的代数。
2.4 重启算子
由于接收准则的本质是贪心策略,所以算法容易陷入局部最优。基本变邻域搜索(basic variable neighborhood search, BVNS)算法采用扰动算子在每次寻优前对被探索解进行扰动得到中间解,从而获得全新的邻域解空间并进行探索,从而达到跳出局部最优的目的,但扰动具有随机性,中间解性能有时会劣于当前解,所以增加了寻优过程的波动性。
为跳出局部最优,实现Pareto前沿解集的推进并同时保证算法稳定性,本文设计了一种新型重启算子来替代扰动算子。
2.4.1自适应阈值
非支配解集连续未获得实质性推进的代数是判断何时重启的关键,将它作为重启算子的启动阈值,记为g。若阈值取值过小,将导致频繁执行重启算子并错过满意解;若阈值取值过大,则会迟迟不重启从而无法跳出局部最优,浪费CPU时间[19]。
在算法运行过程中,解的性能会随着寻优次数的增大逐渐变优,因此在寻优后期相比前期更容易陷入局部最优。针对不同规模的装配线平衡问题,陷入局部最优的可能性与工序数n、工位数m、操作时间不同的工序个数a以及优先关系约束强度R有关。在确定上述因素与重启阈值的函数关系之后,当前寻优代数自适应重启阈值g依据下式确定:
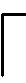
(12)
(13)
(14)
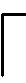
以基准案例Hahn中53工序4工位、Arcus2中111工序12工位以及Scholl中297工序26工位情况为例,重启算子中自适应阈值g随着算法迭代次数r动态变化曲线如图3所示。图3中,go为关于迭代次数的实际阈值函数。图3显示,随着迭代次数r的增大,go曲线的斜率不断减小,并且在寻优前期下降迅速,中后期趋于缓慢,这说明前期非支配解集能够快速向真实前沿推进,中后期逐渐接近真实前沿。因此go的增长趋势在不断减缓,且向上取整后得到的每个g值持续代数增大。自适应g值曲线动态变化与算法在求解过程中陷入局部最优的趋势吻合。

(a)Hahn(53工序4工位) (b)Arcus2(111工序12工位) (c)Scholl(297工序26工位)图3 不同规模案例值曲线Fig.3 Curves of the values of g,go and for different scale cases
2.4.2自适应邻域结构
当d>g时,执行重启算子,即在当前非支配解集中随机选择一个候选解并记录此时刻的重启时间节点tr,并进入重启后的变邻域搜索(variable neighborhood search after restart, VNSAR)对候选解进行探索。与VNSBR阶段不同的是该阶段的多种邻域结构是自适应的,每一次执行重启更新该阶段的邻域结构规模时依据下式进行:
(15)
式中,Round(·)表示四舍五入取整。
式中,KM随寻优进程动态变化,表示当前时间节点重启执行后的邻域搜索阶段的邻域规模;Tt是算法最大寻优总时间;K为全部邻域结构的个数。
随寻优进程的推移,该阶段邻域空间不断扩大,从开始时只有性能最优的重排式邻域空间逐步扩展到全邻域空间。这是因为在寻优前期,重启之后要立即将探索重点放在更容易产生满意解的邻域空间中以快速跳出局部最优,到中后期非支配解集中的解已接近满意解,此时要将探索重点放在更广阔的邻域空间中,防止满意解丢失。
2.4.3基于空间距离的选择策略
在执行完毕重启算子与重启后的变邻域搜索后,可以获得最新的Pareto前沿解集。此时,为确保进入下一次重启前的变邻域搜索阶段的候选解具有良好的多样性,本文基于空间距离最大策略从当前非支配解集中选择候选解。
每个解的适应度值(C0,Pl,Cl)都可视为三维空间中的一个点。显然,Pareto前沿解集中与所有解距离之和最大的解就是位于最不拥挤区域的解,即为当前解集中多样性最好的解,选此为候选解进入下一次重启之前的变邻域搜索阶段。至此,多目标重启变邻域搜索算法执行完毕,其伪代码如下所示。
算法2MORVNS
1: Input:n,m,R,Pn×n,ti
2: Begin:
3: Generate aninitialPOS;
4: Find the initial solutionΩ;
5:d=0;
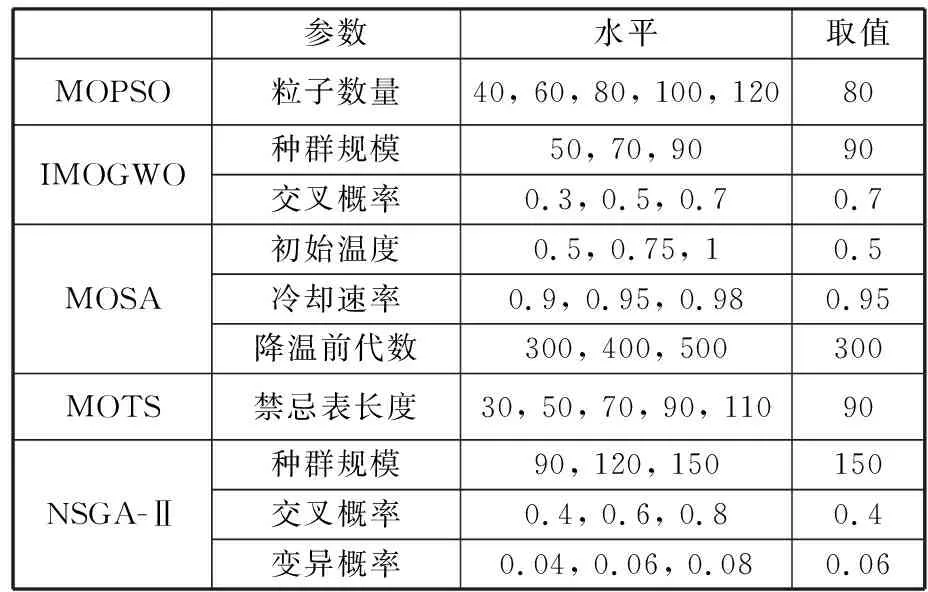
6: Whiletp 5: Forr=1 toβdo 6:g=G(n,m,Pn×n,ti); 7: (Ω,POS,d)=VNSBR(Ω); 8: Ifd>gthen 9: (Ω,POS,d)=VNSAR(Ω); 10:S=D(POS); 11: End If 12: End For 13: End While 14: Output:POS 算法2中,tp表示算法当前寻优总时间;β为足够大的正整数;G为阈值g的生成函数;D为基于空间距离的候选解选择函数。 为证明重启算子、交替搜索策略以及多目标重启变邻域搜索算法的有效性和优越性,本文采用MATLAB R2018a编程,电脑配置为:Intel(R) Core(TM) i5-6200U CPU @2.30GHZ 2.40GHZ and 4.00GB RAM;预防维护情形全部基于装配线平衡问题标杆案例生成,且每次计划随机选择一个工位进行维护,标杆案例数据来自装配线平衡专业网站[20];在进行算法对比时,选取30个案例进行实验,每个案例运行8次,算法运行的终止条件设置为tp≥Tt,算法最大寻优总时间Tt=ρn2/1000,其中ρ=10。 以案例Hahn中53工序6工位情况的运行结果来说明预防维护下装配线平衡多目标优化模型的优势,其甘特图见图4。其中,横轴表示每个工位上的工序操作时间,纵轴表示工位序号;图4a表示正常工作情形下的工序安排,图4b表示对工位2进行维护的工序安排。 (a)正常工作时最佳工序安排 (b)预防维护时最佳工序安排图4 案例Hahn(53工序6工位)不同情形下的工序安排Fig.4 Tasks arrangement of Hahn(53 process 6 work station) in different scenarios 由图4可知,该方案目标值为(2400, 23, 2823),说明正常工作的生产节拍为2400个单位时间,工位2维护情形的生产节拍为2823个单位时间,状态切换时对23道工序进行了调整。若不考虑预防维护,当某工位发生故障时需要对其进行纠正性维护,此时整条线处于停工状态。假设对一个工位维护的时间为x小时,产线的产值为每小时e万元,则直接损失ex万元。当考虑预防维护来进行装配线平衡时,维护与生产在相同时刻进行,则损失仅为工序调整所需时间与成本,调整时间远小于工位维护时间,随行夹具以及各装置调整成本也远远小于工位维护成本,由此可见,与不考虑预防维护的装配线平衡相比,将预防维护提前考虑,能有效保证生产连续性、降低维护时的损失。 为全面评价算法的性能,本文选取世代距离(GD)DGD、逆世代距离(IGD)DIGD和超体积率(HVR)RHVR来判断算法所得Pareto前沿解集的优劣[21]。 (1) 收敛性评价指标DGD用来衡量算法所求得的近似前沿解集Su与真实Pareto前沿解集之间的逼近程度。DGD(Su)值越小,说明Su与真实前沿PTP逼近程度越高,收敛性越好。计算如下: (16) (17) (2)逆世代距离DIGD同时评价解集收敛性与分布性,通过衡量真实前沿逼近Su的程度来判断Su的优劣。DIGD(Su)越小,说明解集Su的综合性能越好。计算如下: (18) (19) (3)综合性评价指标RHVR通过计算Su与参考点σ形成的超体积占真实前沿PTP与参考点σ形成的超体积的比率。参考点σ应该被所有的解支配,将所有解进行归一化后,选取(1,1,1)为参考点。RHVR(Su)值越接近1,说明Su的综合性能越好。计算如下: (20) (21) 式中,VHV为解集S与参考点σ围成的超体积;VOL(·)为勒贝格测度。 3.2.1搜索策略的有效性 为验证多邻域结构搜索时交替搜索策略的有效性,将MORVNS与多目标重启随机邻域搜索算法(MORSNS)以及多目标重启全局邻域搜索算法(MORGNS)进行对比实验。为确保实验的公平性,算法均采用所设计的重启算子、相同的邻域结构和排列方式以及初始解生成策略。 采用不同搜索策略的算法分别对30个标杆案例进行8次对比实验,所有基准案例所得结果GD、IGD以及HVR的均值的95%置信区间如图5所示。由图5可以看出,算法MORVNS获得的非支配解集相比于算法MORSNS和MORGNS获得的非支配解集在GD、IGD以及HVR评价指标上都具有良好的表现,这说明多种邻域结构的交替搜索策略的性能优于随机邻域搜索以及全局邻域搜索策略。 图5 三种算法30个案例的GD、IGD与HVR均值的95%置信区间Fig.5 95% confidence interval for means of GD、IGD and HVR in 30 cases of three algorithms 3.2.2重启算子的有效性 为了证明重启算子的有效性,将所提多目标重启变邻域搜索算法(MORVNS)与多目标基本变邻域搜索算法(MOBVNS)进行对比实验。为确保实验的公平性,MORVNS与MOBVNS均采用相同初始解生成方法和搜索策略、邻域结构及其组合方式,并且在MOBVNS中根据性能较好的重排式邻域结构设计扰动算子。 两种算法对比结果通过30个案例的GD、IGD与HVR均值的95%置信区间图显示,如图6所示。从图6中可以看出,MORVNS得到的Pareto前沿解集的收敛性、多样性以及综合性能都显著优于MOBVNS得到的非支配解集,因此,为跳出局部最优所设计的重启算子是有效的。 图6 两种算法30个案例的GD、IGD与HVR均值的95%置信区间Fig.6 95% confidence interval for means of GD、IGD and HVR in 30 cases of two algorithms 为了能够更好地分析所提出算法的综合性能,将所提多目标重启变邻域搜索算法与改进多目标灰狼算法(IMOGWO)[9]和多目标粒子群算法(MOPSO)、多目标模拟退火算法(MOSA)、多目标禁忌搜索算法(MOTS)、带精英策略的快速非支配排序遗传算法(NSGA-Ⅱ)[22]进行对比实验。其中,MOSA与MOTS两种局部搜索算法均采用和本文算法相同的邻域结构以及初始解生成方式。 在实验进行之前,运用Minitab 18中田口实验方法确定各个算法之中的参数,由于所提算法参数自适应,所以不对其进行参数校验。各对比算法参数校验结果如表1所示。 表1 各测试算法参数校验结果Tab.1 Parameter validation results of test algorithms 在各对比算法参数确定之后,对30个案例进行实验得到的结果如表2所示,所选取的评价指标GD、IGD以及HVR的均值的95%置信区间如图7所示。 分析表2与图7可知,所提算法MORVNS获得的非支配解集相比其余测试算法所得的非支配解集的GD值与IGD值更接近于0、HVR值更接近于1,这说明所提算法在解决预防维护下装配线平衡多目标优化问题上具有出众的表现,所得非支配解集拥有较好的收敛性以及多样性。 表2 各测试算法实验结果Tab.2 Experimental results of test algorithms 图7 各测试算法30个案例的GD、IGD与HVR均值的95%置信区间图Fig.7 95% confidence interval for means of GD、IGD and HVR in 30 cases of test algorithms 以大规模标杆案例Scholl中具有297工序26工位的情况为例说明所有测试算法获得的Pareto解集在三维空间中的分布状态,如图8所示。 图8 Pareto前沿在三维空间中的分布Fig.8 Distribution of Pareto front in 3D space 分析图8可知,MORVNS得到的非支配解集在一定程度上能够支配改进多目标灰狼算法以及其余四种经典多目标算法得到的前沿解集,并在收敛性较好的基础上获得数量较多的满意解。 综上所述,所提算法获得的前沿解集具有较好的综合性能,因此所提MORVNS能够获得具有竞争性的Pareto前沿解集。 本文以最小化设备正常工作、预防维护情形下的生产节拍以及工序调整为目标,构建预防维护下装配线平衡的多目标优化数学模型,并提出多目标重启变邻域搜索算法来解决该问题,所提算法具有以下特点: (1)实现四类能够直接生成可行解的邻域算子,并根据各算子性能对其进行组合排序。 (2)探索多邻域结构搜索策略,并从理论与实验两方面验证交替搜索为最有效的搜索方式。 (3)设计重启策略跳出局部最优,并以自适应重启阈值作为判断是否重启的条件。 (4)参考寻优进程逐渐扩大重启后的邻域空间,并基于空间距离选择进入下次重启前的待探索解,从而有针对性地对特定解与特定邻域空间进行重点搜索。 实验证明本文所提算法能获得综合性能较好的非支配解集。决策者可以在不同性能且具有竞争性的多个非支配解中进行选择,更好地指导实际生产。后续工作将对预防维护与其他类型以及更符合现场的装配线平衡问题进行集成,并考虑成本、能耗和负载等多个目标。3 实验分析
3.1 案例分析

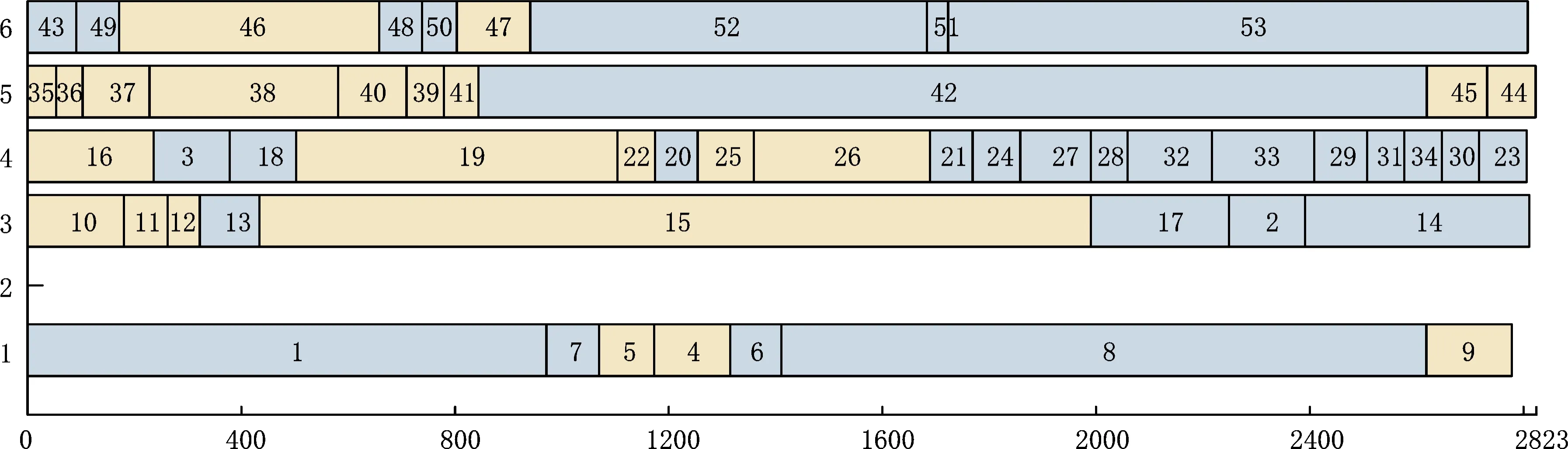
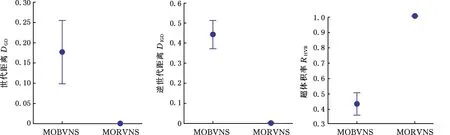
3.2 有效性分析



3.3 综合性能分析
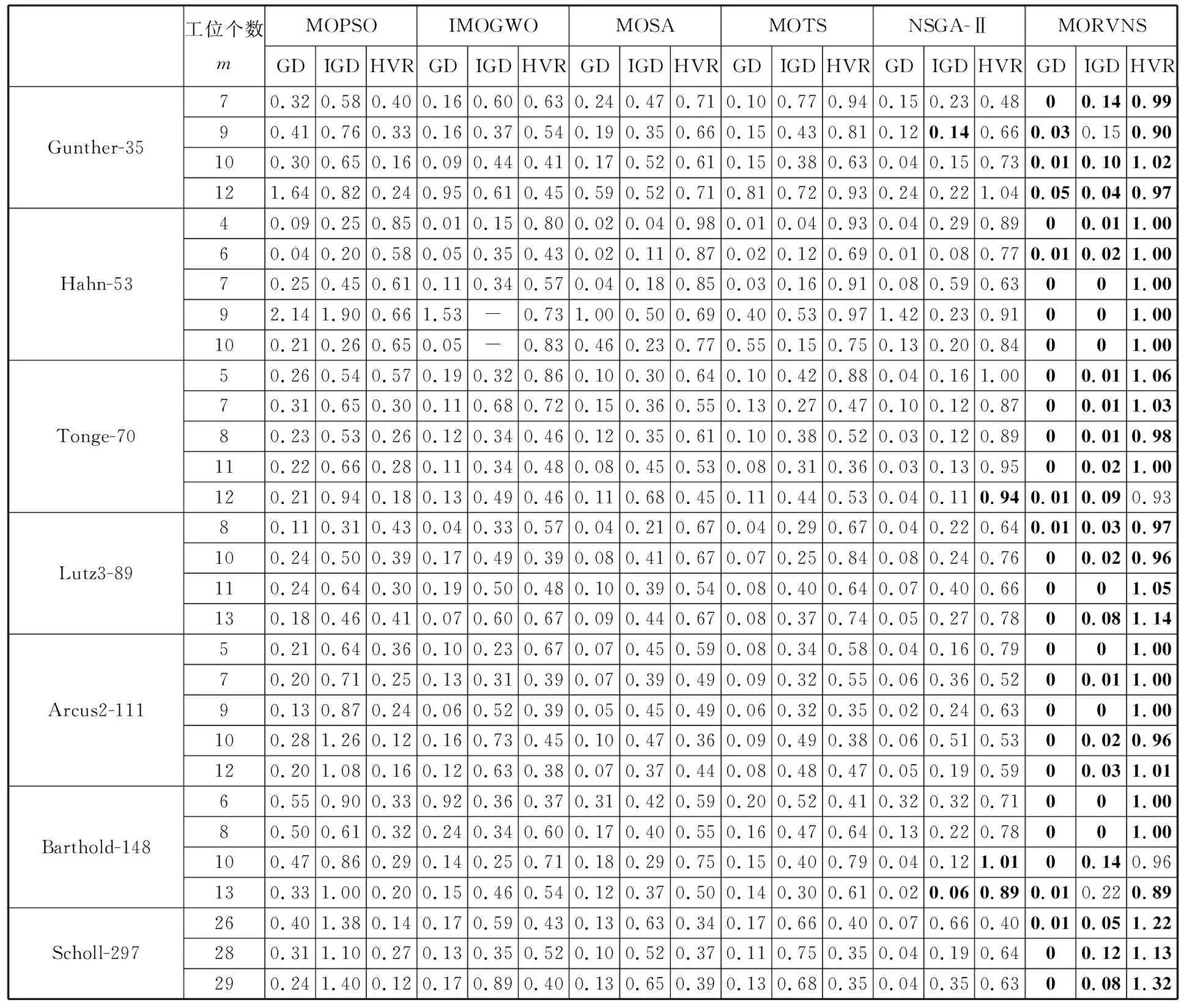
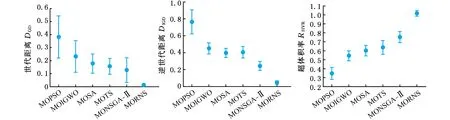
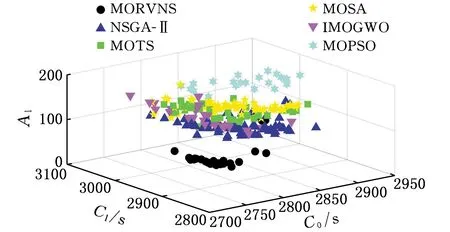
4 结论

