低频输电技术原理之二——M3C 的稳态特性与主回路参数设计

徐 政，张哲任

（浙江大学 电气工程学院，杭州 310027）

0 引言

M3C（模块化多电平矩阵变流器）的主回路包括输入侧和输出侧的联接变压器、每个桥臂的电抗器、子模块电容器、IGBT（绝缘栅双极型晶体管）模块等一次设备。主回路设备参数选择是M3C换流站设计的重要组成部分，合理的主回路设备参数可以有效改善系统的动态和稳态性能，降低系统的初始投资及运行成本，提高系统的经济性能指标。主回路设备参数选择的依据是M3C 的稳态运行特性和暂态运行特性。以往关于高压大容量M3C 的研究主要集中在建模和控制方面[1-14]，关于主回路元件参数设计的研究很少，文献[15]曾对子模块电容参数的选择进行过研究，但离实际工程应用还有差距。本文将首先对M3C 的稳态运行特性进行分析，然后根据稳态特性的分析结果，探讨一下桥臂子模块数目和子模块电容值的设计方法。至于联接变压器和IGBT 模块等设备参数的选择，可以基本照搬MMC（模块化多电平换流器）对应设备参数的设计方法[16]。桥臂电抗器参数的选择则主要取决于暂态故障电流的抑制需求，稳态下对其参数的选择并不构成严格的约束。

1 桥臂电流与输入侧和输出侧电流之间的关系推导

为了便于阅读，将文献[17]已经详细介绍过的M3C 拓扑结构和物理量命名重新给出，如图1所示。由图1 可见，M3C 具有9 个桥臂，对M3C的主回路参数设计主要是确定每个桥臂的组成元件及其参数，包括桥臂电抗器、串联的子模块数目、子模块的开关器件参数以及子模块电容器的参数。而考虑的运行条件包括稳态运行条件和故障引起的暂态运行条件。显然，M3C 的9 个桥臂的稳态运行特性是主回路参数设计的基础，因此以下推导桥臂电流和电压的稳态特性。

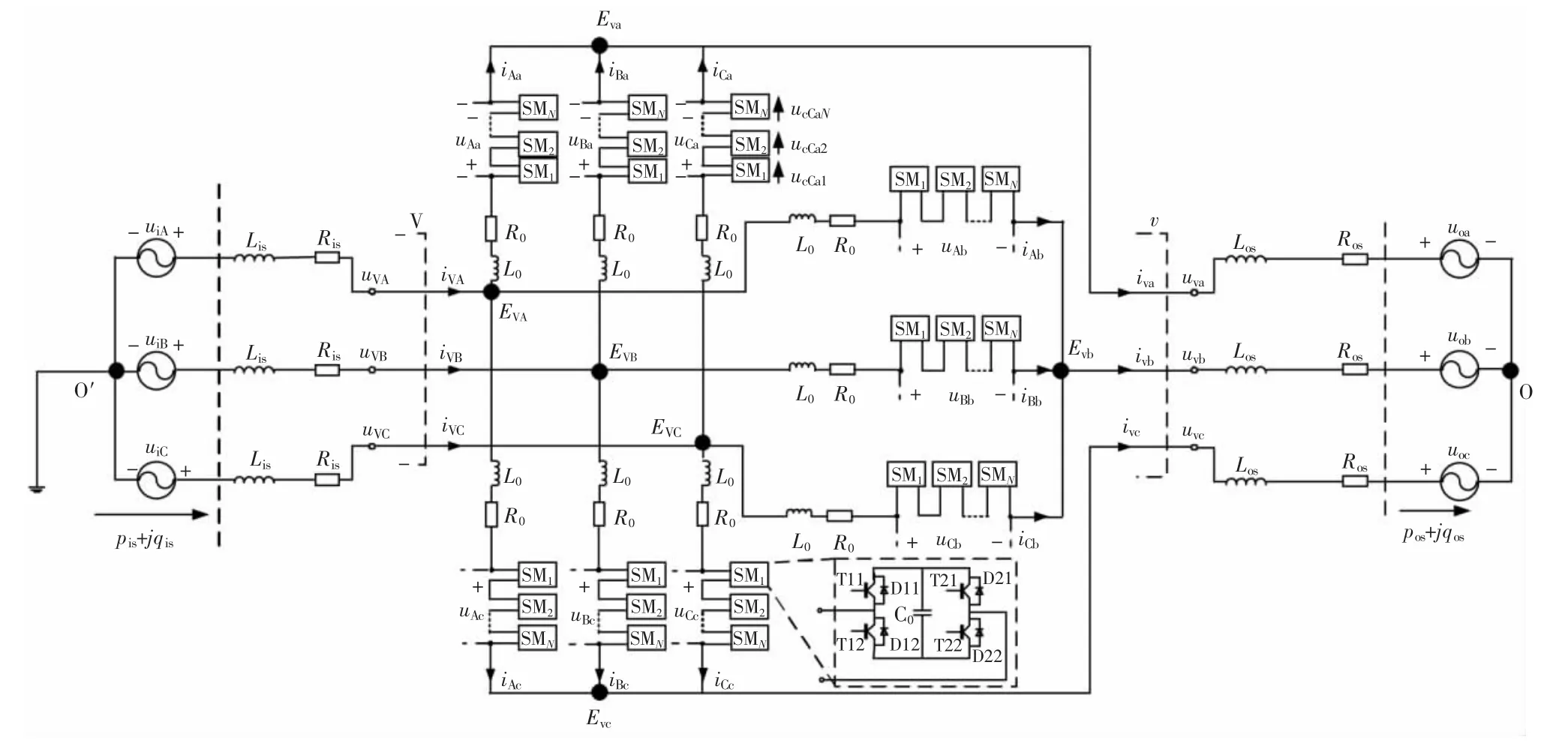
图1 M3C 拓扑结构示意

根据基尔霍夫电流定律，M3C 输入侧交流电流与桥臂电流之间的关系为：

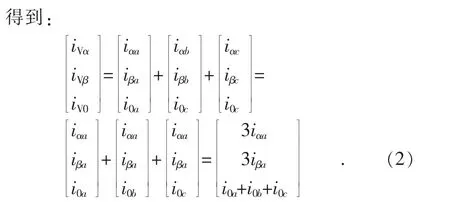
根据文献[17]中式（21）和输出侧交流系统对称的条件有：

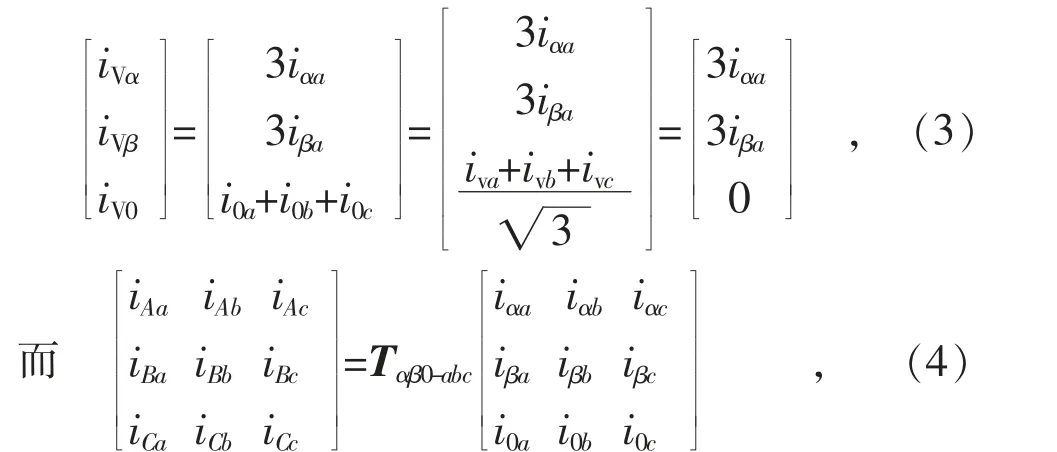
根据环流为零条件和式（3）有：

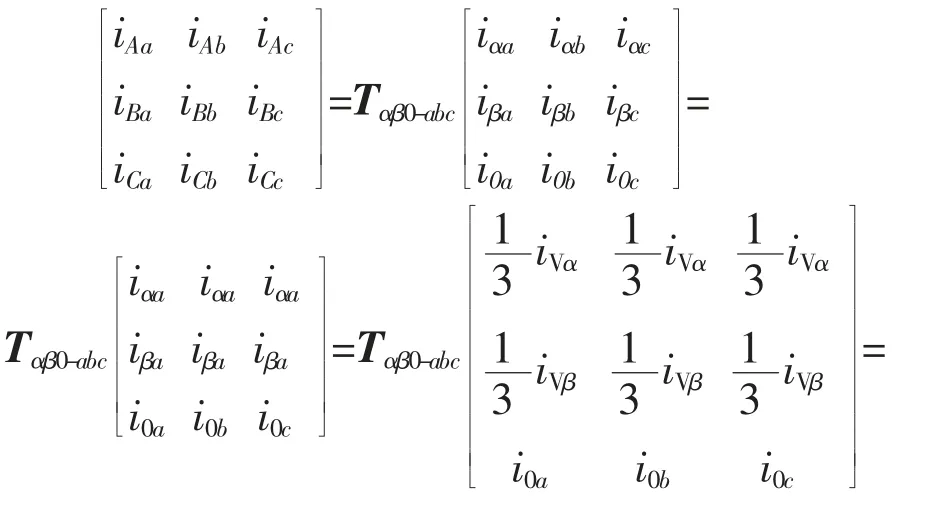
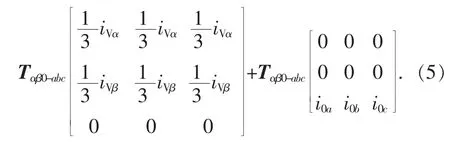
利用输入侧交流系统对称从而iV0=0 的条件，根据式（5）有：

再根据文献[3]中式（21）有：

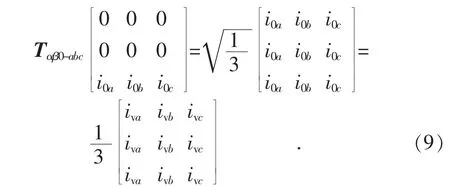
从而根据式（6）、式（7）和式（9）有：

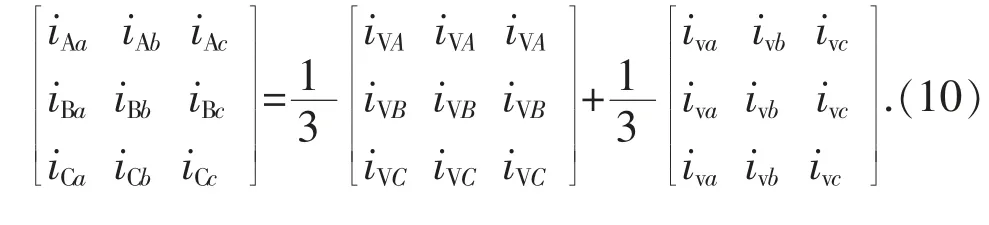
需注意式（10）是在环流为零的条件下导出的。

2 M3C 桥臂子模块数N 的确定

以图1 中Aa 桥臂为例列写电压方程，有：

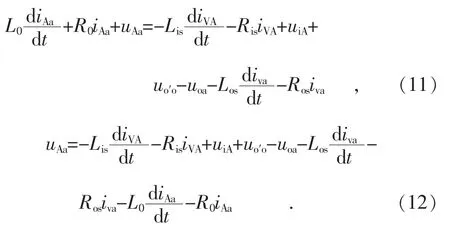
在输入侧和输出侧对称且环流控制到零的条件下，根据式（10）有：

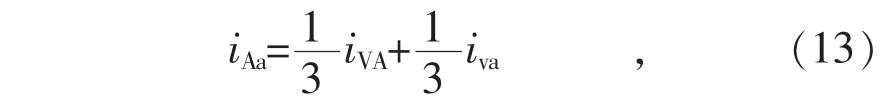
因此式（12）变为：

将式（20）中的每一项都取其最大值，然后求其代数和，则得到的桥臂电压最大值为：

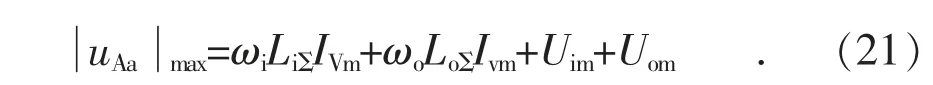
注意，式（21）中的桥臂电压最大值可以理解为考虑了M3C 所有运行工况下的最大值。设子模块电容电压的额定值为Uc，则单桥臂应采用的子模块数目为：

3 子模块电容值的确定方法

子模块电容值的选择取决于子模块电容电压的波动幅度，直接求取子模块电容电压表达式比较困难，因此仿照MMC 中求子模块电容电压表达式的方法[16]，先求出子模块电容电流的表达式，然后根据电容电流与电容电压之间的关系求出子模块电容电压。以下参考文献[16]建立MMC 子模块电容电流和电容电压集合平均值模型的做法，基于开关函数法，推导出子模块电容电流集合平均值与桥臂电流以及子模块电容电压集合平均值与桥臂电压之间的关系。

3.1 子模块电容电流集合平均值与桥臂电流的关系[16]

定义SXy_i为X 相y 桥臂第i 个子模块的开关函数。它的值取1 表示该子模块正投入，取-1 表示该子模块负投入，取0 表示将该子模块切除。同时定义X 相y 桥臂平均开关函数

平均开关函数表示桥臂中子模块的平均投入比。

首先推导子模块电容电流集合平均值与桥臂电流之间的关系。桥臂电流通过子模块的开关动作耦合到子模块的直流侧，这部分电流流过子模块电容，称为电容电流。电容电流的正方向与图1标出的桥臂电流正方向一致，定义为电容充电方向。对于X 相y 桥臂的第i 个全桥子模块，流过其电容器的电流满足：

对该桥臂所有子模块求和：

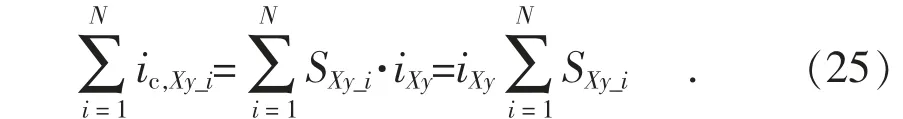
式（25）左右两边同时除以子模块个数N 得：

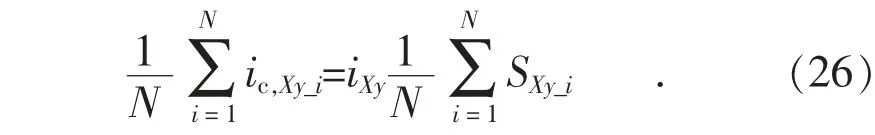
将式（23）代入式（26）得：

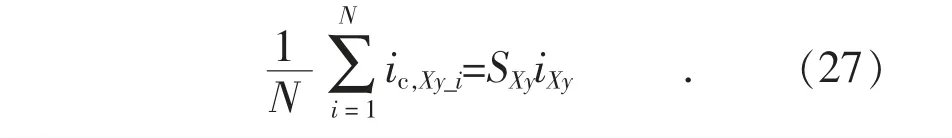
定义X 相y 桥臂子模块电容电流集合平均值为：

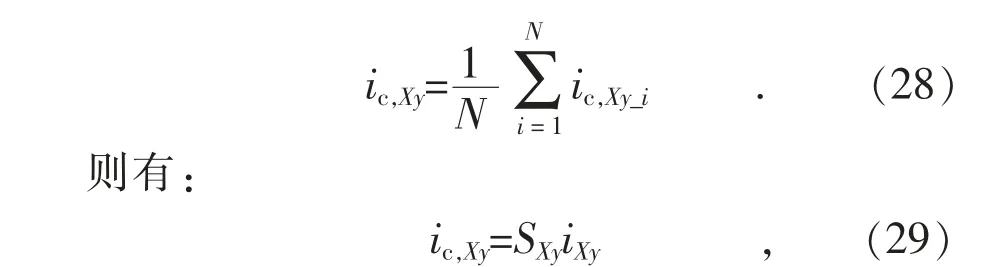
式（29）就是子模块电容电流集合平均值与桥臂电流之间的关系。

3.2 子模块电容电压集合平均值与桥臂电压的关系[16]

以下推导子模块电容电压集合平均值与桥臂电压之间的关系。电容电压通过子模块的开关动作耦合到桥臂中。X 相y 桥臂第i 个子模块耦合到桥臂中的电压usm，Xy_i，可以用开关函数表示为：

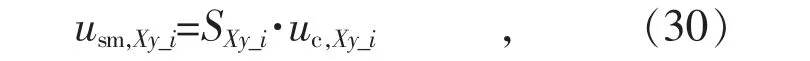
式中：uc，Xy_i为X 相y 桥臂第i 个子模块的电容电压。

对该桥臂所有子模块耦合到桥臂中的电压求和有：

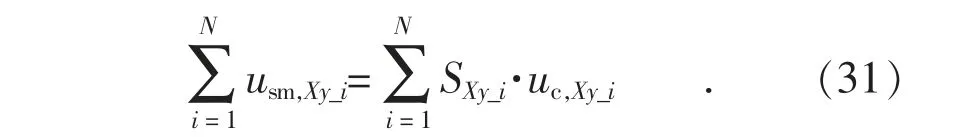
由于本文关注的是子模块电容电压集合平均值与桥臂电压之间的关系，因此假设所有子模块完全相同，单个子模块的电容电压uc，Xy_i等于所有子模块电容电压的集合平均值uc，Xy，因此有：

将式（23）代入式（33）可得：

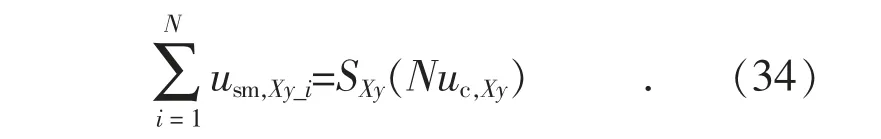
式（34）左边即为X 相y 桥臂的电压uXy。这样，式（34）可以重新写为：

3.3 子模块电容电流集合平均值解析表达式

以下推导X 相y 桥臂所有子模块电容电压的集合平均值uc，Xy的解析表达式。采用逐次逼近法进行推导[16]。

第一步，令：

则根据式（35）有：

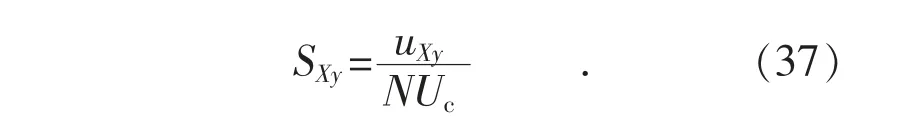
以A 相a 桥臂为例进行推导，由式（29）：

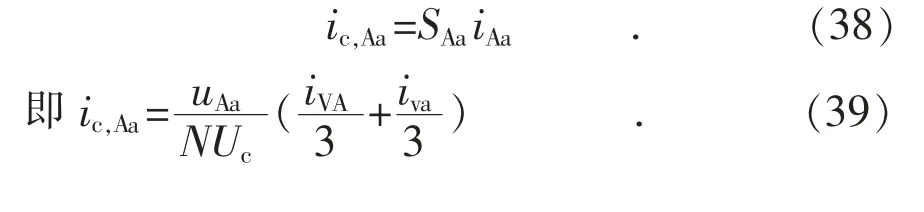
根据式（39）、式（20）、式（17）、式（18）有：

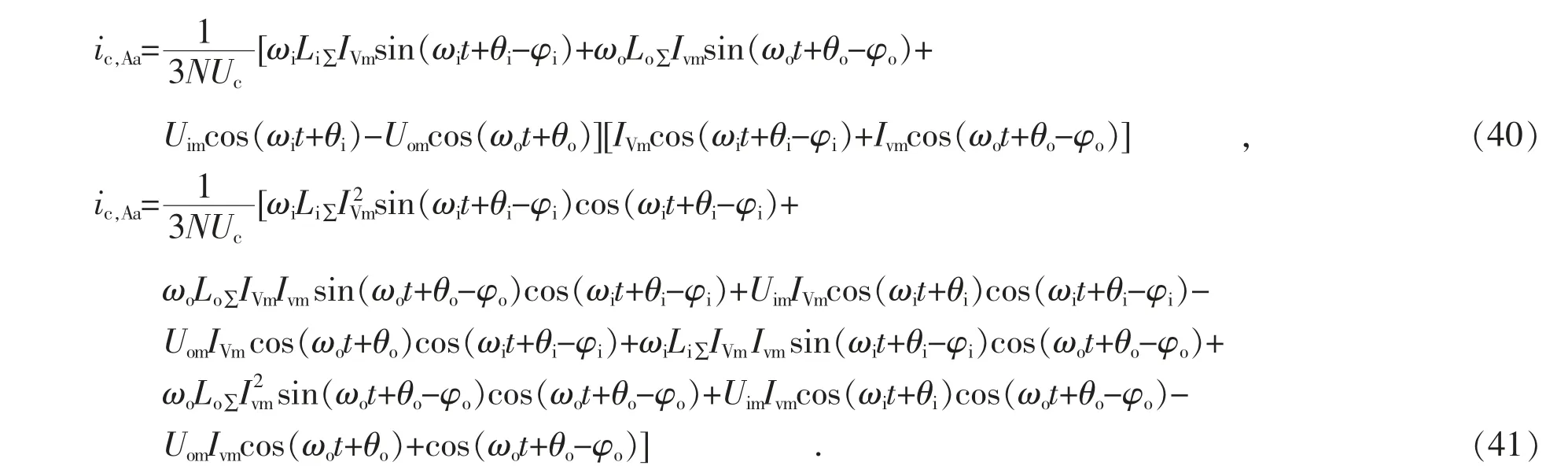
将式（41）中的正弦函数乘积项展开，可以得到：

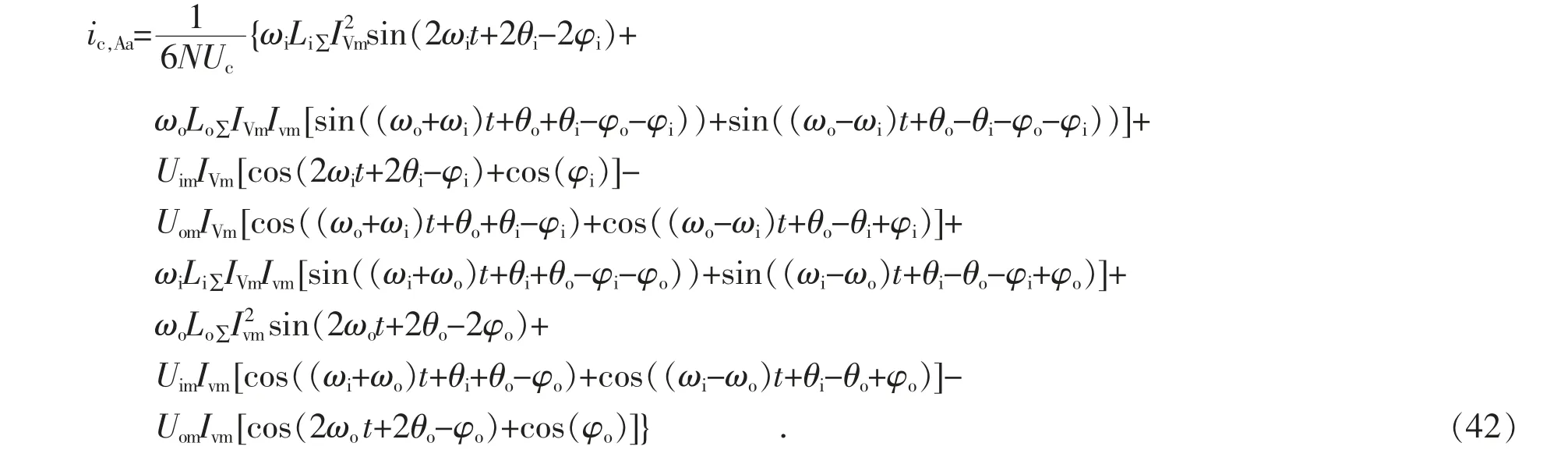
式（42）中含有直流分量，在稳态运行情况下，子模块电容电流的直流分量应该为零，否则将产生无穷大的电容电压。这样，子模块电容电流集合平均值的表达式可重写为：

这样，可以得到子模块电容电压的集合平均值为：

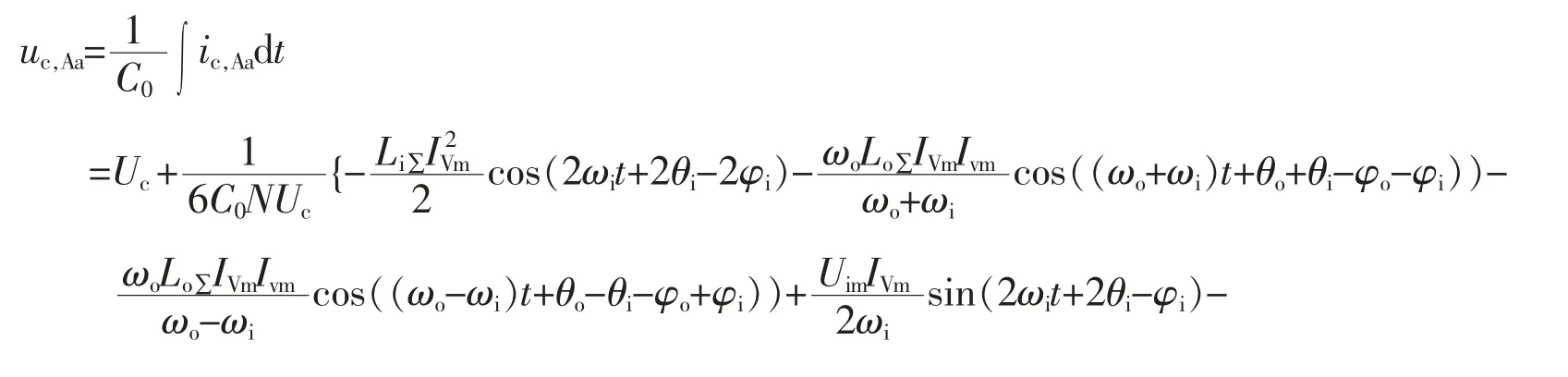
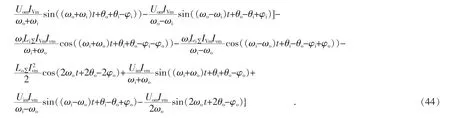
在输入侧和输出侧系统频率、电压、电流以及系统两侧电抗和桥臂电抗给定的条件下，式（44）的花括号中的表达式为θi，φi，θo，φo，t 共5 个变量的函数。由于θi和θo是两侧系统电压的初相角，两者之间只有相对的意义，因此可以设定其中一个为基准值，不妨设定θi为基准相角，即设定θi=0。这样式（44）的花括号中的表达式就是φi，θo，φo，t 共4 个变量的函数，用λ（φi，θo，φo，t）来表示，即：

现在的目标是求λ（φi，θo，φo，t）的最大值，其直接与子模块电容电压的正向波动幅值成正比。完全基于数学优化方法求λ（φi，θo，φo，t）的最大值并不容易，但是根据M3C 的物理功能，通过对λ（φi，θo，φo，t）本身的分析，可以确定λ（φi，θo，φo，t）取到最大值的条件如下：

1）设置两侧系统初始相角差为0°，即θo=0°。

2）输入侧和输出侧都处于有功为零、无功满出力状态，即φi=±90°，φo=±90°。

在θo，φi和φo给定的情况下，λ（φi，θo，φo，t）仅仅是单变量t 的函数。对应条件2）的4 种组合，分别画出λ（φi，θo，φo，t）在一个周期上的曲线，取出4 条曲线中的最大值进行比较就很容易得到λ（φi，θo，φo，t）的最大值，设λ（φi，θo，φo，t）的最大值为λmax。这样，根据式（44），子模块电容电压的正向最大波动幅度为：

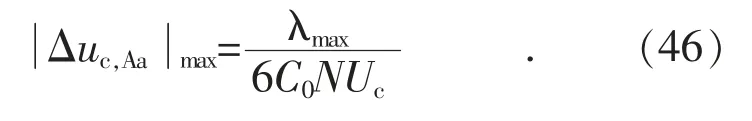
从而根据对子模块电容电压最大正向波动幅度大小的要求，确定子模块电容的值。

4 桥臂电抗器参数设计

桥臂电抗器的功能主要有两个：第一个功能是充当与电网侧之间的联接电抗器用；第二个功能是限制流过桥臂的故障电流上升率，为子模块开关器件的自保护赢得时间。但根据文献[17]的M3C 等效电路，桥臂电抗除以3 后才与联接变压器漏抗一起构成联接电抗，因此桥臂电抗器对联接电抗的贡献比较小，即联接电抗的取值不对桥臂电抗取值构成硬约束。这样，桥臂电抗的取值主要就由其第二个功能决定。为了满足对桥臂故障电流上升率进行限制的要求，需要对M3C 可能发生的各种故障进行扫描，从而确定桥臂电抗的值，这里特别要注意的故障类型包括联接变压器阀侧短路故障和桥臂间短路故障等。

5 实际算例

设某M3C 输入侧接海上风电场，输出侧接陆上电网，额定容量为Si=So=330 MVA，Uim=Uom=65.3 kV，IVm=Ivm=3.368 kA，ωi=2π×20=125.7 rad/s，ωo=2π×50=314.2 rad/s，LiΣ=15.4 mH，Lo∑=6.17 mH，子模块电容电压额定值为Uc=1.6 kV，假定要求的子模块电容电压正向波动率小于10%，试确定桥臂子模块数N 和子模块电容器的电容值。

求解过程如下：

根据式（21）得

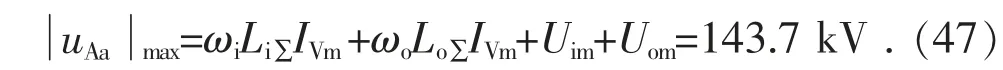
对式（45）的λ（φi，θo，φo，t）求最大值。根据物理意义和工程经验，λ（φi，θo，φo，t）有可能取到最大值的点对应的θo的取值可能为0°，90°，180°和270°，φi的取值可能为0°，+90°和-90°，φo的取值可能为0°，+90°和-90°。因此分别画出θo取0°，90°，180°和270°的4 种情况下λ（φi，θo，φo，t）随时间t 的变化曲线如图2 所示。

由图2 可以看出，本算例条件下子模块电容电压出现正向波动幅度最大的工况是φi=-90°，φo=-90°，λmax的取值与θo无关，不同的θo仅仅起到λ（φi，θo，φo，t）曲线在时间轴上平移的作用，不改变λ（φi，θo，φo，t）曲线的幅值。根据图2 的实际算例结果，结合M3C 的物理特性和工程经验，说明第3.3 节关于求λ（φi，θo，φo，t）最大值的简化计算条件是合适的。

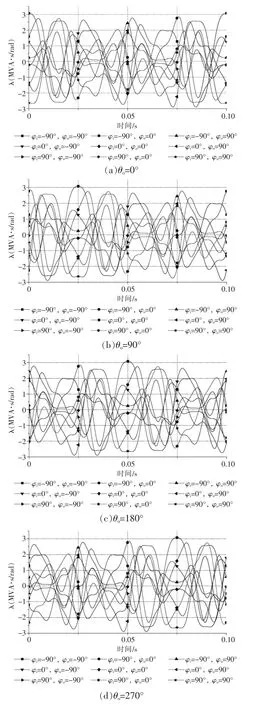
图2 λ 随t 变化的曲线

对于本算例，λmax=3.08 MVA·s/rad，根据式（46）可以得到：

6 讨论与小结

本文在环流为零的条件下推导了M3C 桥臂电流与输入侧、输出侧电流之间的关系，同样在环流为零的条件下导出了子模块电容电流集合平均值的解析表达式和子模块电容电压集合平均值的解析表达式。在此基础上给出了确定桥臂子模块数目的算法和设计子模块电容值的公式。实际工程中，由于环流对M3C 输入侧和输出侧的行为并没有任何影响，且环流的存在并不会产生其他积极的作用，因此在M3C 控制器设计时，目标之一就是将环流控制到零。本文在环流为零的条件下推导的M3C 桥臂电流电压以及子模块电流电压表达式满足一般工程条件，可以作为M3C 主回路元件参数设计的理论基础。本文算例部分对M3C 主回路元件参数设计进行了示范，可为实际工程设计做参考。