特高压变压器调压补偿方式分析与档位选择

谭风雷，陈 昊，刘怀宇

（国网江苏省电力有限公司检修分公司，南京 211102）

0 引言

随着我国经济高速增长，社会用电量屡创新高，为满足电网建设要求，以特高压电网为骨干网架、各级电网协调发展的坚强智能电网得以大规模建设[1-4]。国家能源局发布的《电力发展“十三五”规划（2016—2020 年）》中提出建设特高压与常规输电相结合的输电通道，进一步增加电网建设规模，优化电网主网架，可见特高压电网建设对经济发展起着决定性作用。特高压电网主要由±800 kV 换流站及其输电线路、1 000 kV 变电站及其输电线路组成。1 000 kV 特高压变压器作为1 000 kV 变电站的核心电力设备，承担着升降压的任务，直接影响着电网的安全稳定运行[5-7]。

鉴于1 000 kV 特高压变压器的重要性，许多专家对其进行了深入研究，包括结构设计、调压原理、保护控制、温升控制等[8-12]。但由于特高压变压器电压等级高，很多研究都只能局限于理论分析，缺乏现场试验，从而限制了特高压变压器的应用。在特高压变压器的众多研究方向中，本文选择调压原理作为研究重点。文献[13]以1 000 kV 特高压晋东南站为例，分析了调补变压器差动保护原理及配置，为特高压变压器的安全运行提供参考。文献[14]以1 000 kV 特高压南阳站为例，通过建立仿真模型分析了完全补偿和非完全补偿2 种补偿方式的调压效果。文献[15]通过分析2 种补偿方法各个绕组的电气连接与电磁耦合关系，对其调压结果进行了比对。尽管现有文献对调压原理的相关研究已有很多，但都只是通过仿真分析了调压过程，尚未建立数学模型定量分析，缺乏理论依据。

针对上述问题，本文首先研究了特高压变压器的结构原理及调压补偿方式，分析了非完全补偿和完全补偿2 种方式各绕组间的电气连接与电磁耦合关系。然后以完全补偿方式为例，对特高压变压器的调压过程进行定性分析。最后通过建立2 种补偿方式的数学模型，研究档位选择方法，分析比较了它们的调压效果。

1 特高压变压器结构原理

考虑到1 000 kV 特高压变压器电压高、容量大，为了便于安装与运输，一般都采用单相分体结构。同时鉴于自耦变压器成本低、重量轻等优势，特高压变压器一般都采用自耦变压器[16]。自耦变压器有线端调压和中性点调压2 种调压方式。其中，线端调压一般采用中压侧线端调压，属于定磁通调压；而中性点调压一般是借助中性点进行调压，属于变磁通调压。就特高压变压器而言，其中压侧额定电压为500 kV，若采用线端调压，调压装置的绝缘水平难以满足，使得制造成本过高；若采用中性点调压，具有调压装置绝缘水平低、分接抽头电流小等优势。因此，特高压变压器一般都采用中性点调压方式[17-18]。

中性点调压属于变磁通调压，当分接开关处于不同位置时，中压侧电压与电流、低压侧电压会随之改变。为了减少特高压变压器的电压波动，提高系统运行可靠性，需对低压侧进行补偿。根据变压器调压励磁电源的不同，又分为非完全补偿方式和完全补偿方式。其中，非完全补偿方式结构原理如图1 所示，其PV（调压励磁绕组）电源取自LV（低压绕组）电压；完全补偿方式结构原理如图2 所示，其PV 电源取自LV 和BV（补偿绕组）的电压和，即为低压侧电压。

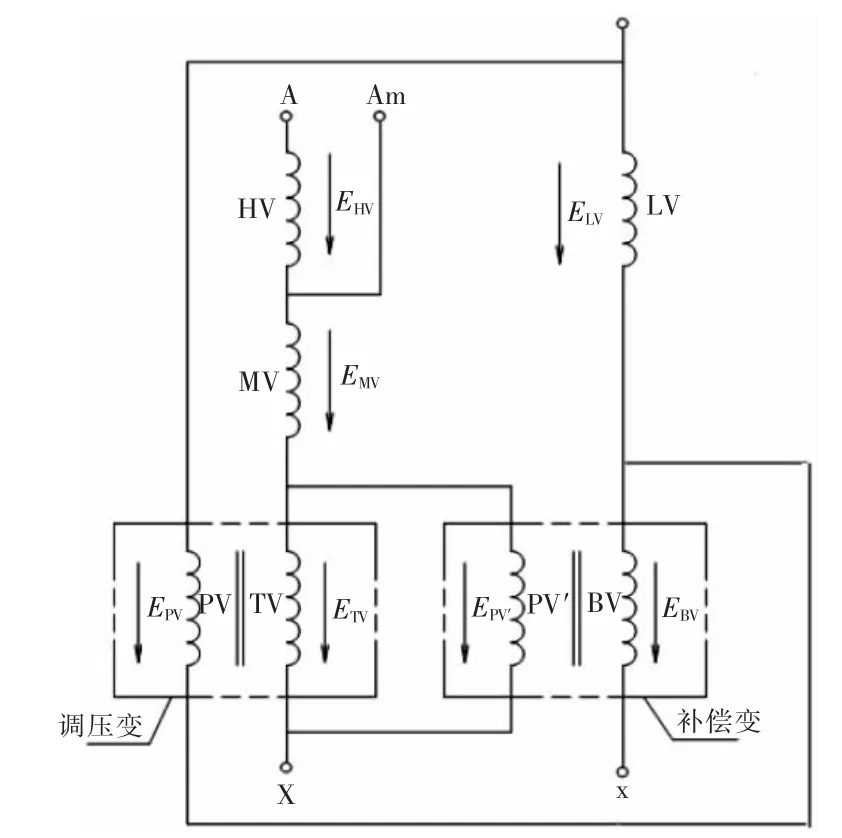
图1 非完全补偿方式结构原理

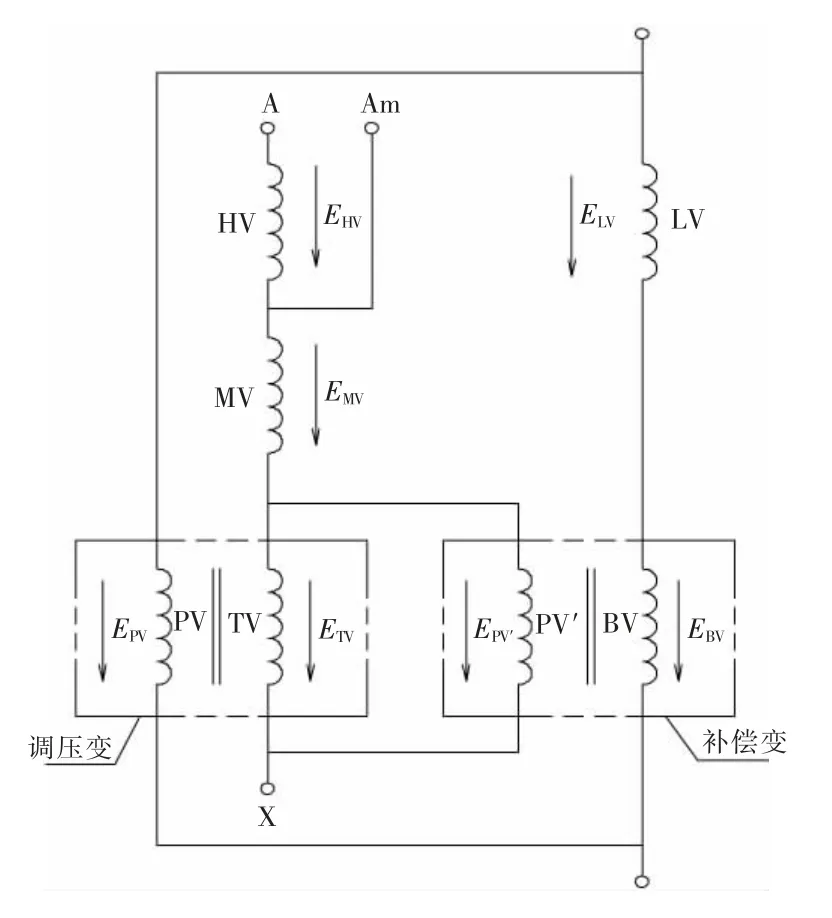
图2 完全补偿方式结构原理

考虑到特高压变压器体积大，一般采用分体结构，包括主体变压器和调补变压器两部分。其中，调补变压器内设置调压变压器和补偿变压器2 个器身，调压开关放置在调补变压器油箱内。主体变压器与调补变压器采用油-空气套管引出，在外部进行连接。

2 特高压变压器调压原理定性分析

由图1 和图2 可知，特高压变压器高压侧与低压侧之间只有电气连接，不存在磁的联系，其中7 个绕组的电磁耦合关系为：高压绕组、中压绕组和低压绕组存在电磁耦合，每匝线圈的感应电动势e1相同；调压励磁绕组和调压绕组存在电磁耦合，每匝线圈感应电动势e2相同；补偿励磁绕组和补偿绕组存在电磁耦合，每匝线圈感应电动势e3相同。

特高压变压器的调压原则为：高压侧电压保持不变；低压侧电压保持不变；调节中压侧电压。以下以完全补偿方式为例来分析特高压变压器的调压过程。根据图2 的电气连接关系，结合上文分析的电磁耦合关系，当分接开关处于正分接时，高压侧电压UH、中压侧电压UM和低压侧电压UL可以表示成：

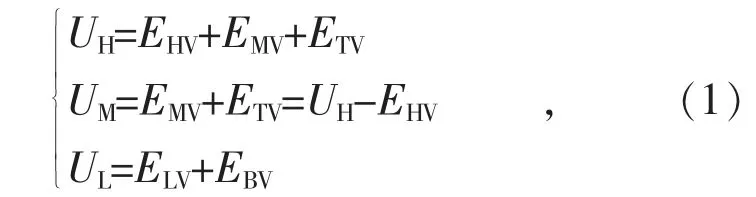
式中：EHV表示高压绕组两端感应电势；EMV表示中压绕组两端感应电势；ELV表示低压绕组两端感应电势；ETV表示调压绕组两端感应电势；EPV表示调压励磁绕组两端感应电势；EBV表示补偿绕组两端感应电势；EPV′表示补偿励磁绕组两端感应电势。

根据UH表达式可知，当分接开关处于正分接时，正向串联TV，由于UH保持不变，ETV正向分压使得EHV和EMV减少，同时HV，MV 和LV有电磁耦合，ELV也减少。根据UM表达式可知，当EHV减少时，由于UH保持不变，使得UM增加，从而实现中压侧电压升高的调节。根据UL表达式可知，由于ETV正向分压使得EPV′增加，EBV随着增加，从而ELV减少，实现低压侧补偿功能，使得UL基本保持不变。

当分接开关处于负分接时，UH，UM和UL可以表示成：

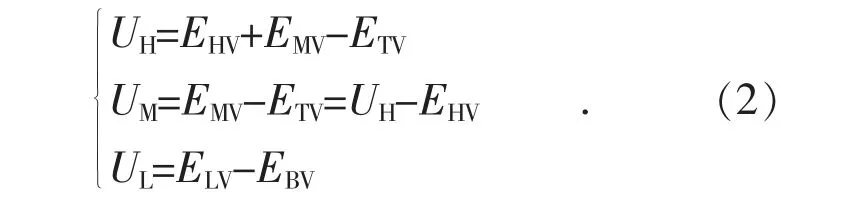
根据UH表达式可知，当分接开关处于负分接时，反向串联TV，由于UH保持不变，ETV反向分压使得EHV和EMV增 加，同时HV，MV和LV有电磁耦合，这时ELV也增加。根据UM表达式可知，当EHV增加时，由于UH保持不变，UM减少，从而实现中压侧电压减少的调节。根据UL表达式可知，由于ETV反向分压使得PV′反向电势增加，EBV随着反向增加，从而抵消ELV的增加，实现低压侧补偿功能，使得UL基本保持不变。

考虑到特高压变压器采用非完全补偿方式时的调压过程与采用完全补偿方式时基本一致，就不再叙述。

3 特高压变压器调压模型

3.1 非完全补偿方式调压模型

根据图1 电气结构，可得非完全补偿方式下的电气表达式：

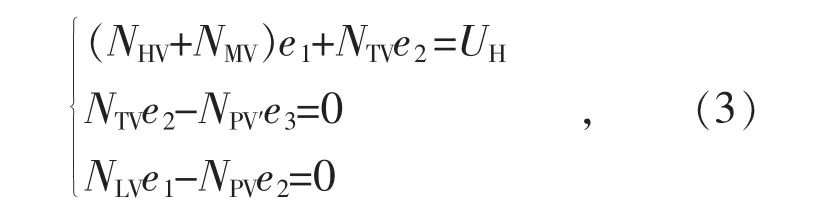
式中：NHV表示高压绕组线圈匝数；NMV表示中压绕组线圈匝数；NLV表示低压绕组线圈匝数；NTV表示调压绕组线圈匝数；NPV表示调压励磁绕组线圈匝数；NBV表示补偿绕组线圈匝数；NPV′表示补偿励磁绕组线圈匝数。

求解式（3）可得：

根据式（4），结合图1 可得非完全补偿方式下UM和UL的表达式：

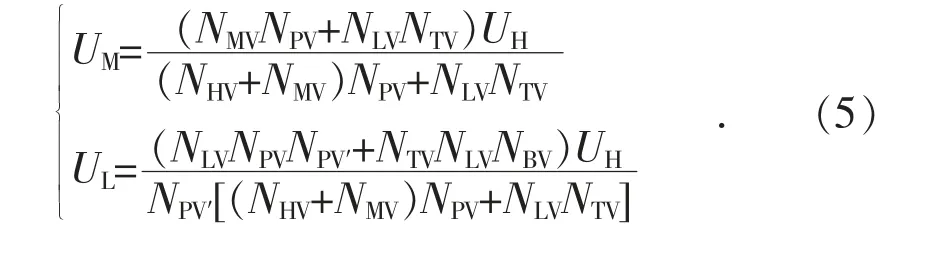
3.2 完全补偿方式调压模型

根据图2 电气结构，可得完全补偿方式下的电气表达式：

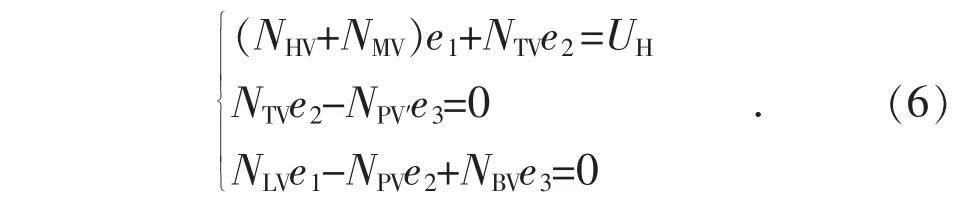
求解式（6）可得：

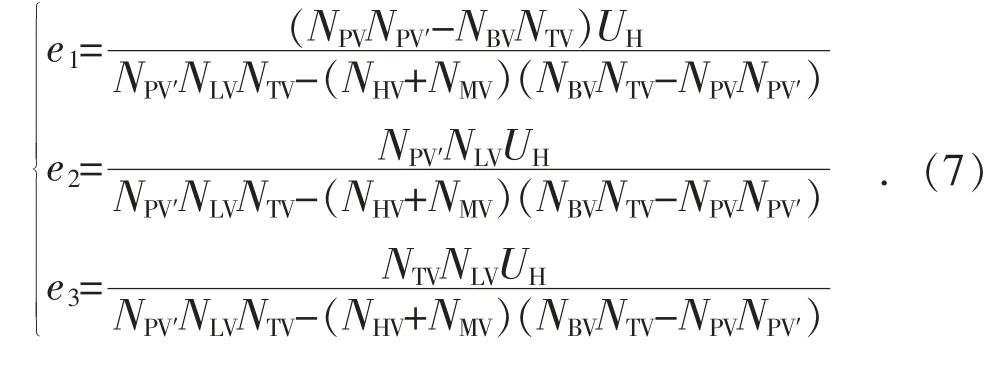
根据式（7），结合图2 可得完全补偿方式下UM和UL的表达式：

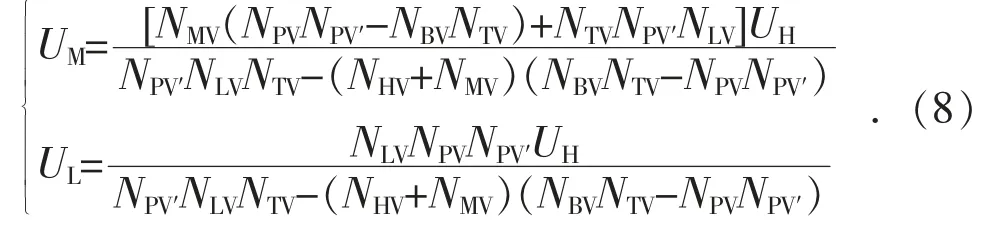
为了便于后文的分析，现定义4 种变量。

1）变量1，低压侧各档位电压相对于低压侧额定电压110 kV 的波动率，其表达式为：

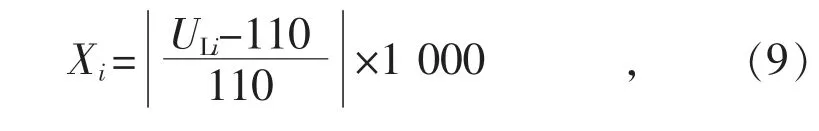
式中：i 表示分接开关档位；Xi表示分接开关处于第i 档时，低压侧电压相对于低压侧额定电压110 kV 的波动率；ULi表示分接开关处于第i 档时低压侧电压。

2）变量2，低压侧各档位电压相对于未调档时低压侧电压（分接开关处于5 档时）的波动率，其表达式为：

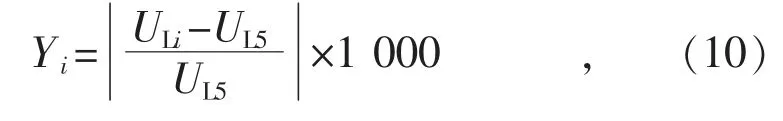
式中：Yi表示分接开关处于第i 档时，低压侧电压相对于未调档时低压侧电压的波动率。

3）变量3，中压侧各档位电压相对于中压侧各档位额定电压的波动率，其表达式为：

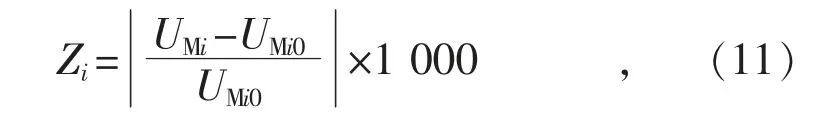
式中：Zi表示分接开关处于第i 档时中压侧电压相对于中压侧第i 档额定电压的波动率；UMi表示分接开关处于第i 档时中压侧电压；UMi0表示分接开关处于第i 档时中压侧额定电压。

4）变量4，分接开关各档位间电压变化率，其表达式为：

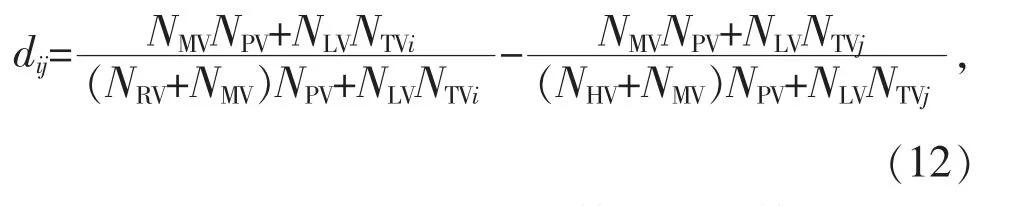
式中：dij表示分接开关处于第i 档与第j 档的电压变化率。

4 档位选择方法研究

上文分析了特高压变压器2 种调压方式的原理，以下研究特高压变压器的档位选择方法，主要包括4 个步骤。

1）步骤一，计算特高压变压器中压侧目标电压UMT。考虑到中压侧目标电压与500 kV 线路对侧电压、线路阻抗、线路电流和系统无功投退情况有关，故中压侧目标电压UMT可以表示为：

式中：U0表示500 kV 线路对侧电压；Z0表示线路阻抗；I0表示线路电流；UI表示110 kV 低压侧电抗器对中压侧电压影响；UC表示110 kV 低压侧电容器对中压侧电压影响。考虑到中压侧目标电压计算比较复杂且不属于本文的研究重点，因此文中假定中压侧目标电压即为中压侧第5 档额定电压。

2）步骤二，确定分接开关的档位范围。计算中压侧目标电压与分接开关处于第5 档时中压侧电压的差值变化率，表达式如下：

根据电压差值变化率D，可以得到分接开关的档位范围，如表1 所示。

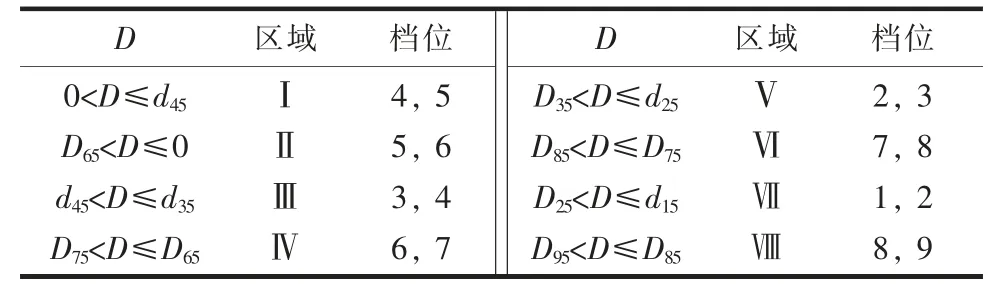
表1 分接开关档位范围与D 值关系

3）步骤三，确认分接开关的档位范围后，计算档位范围内各档位中压侧实际电压相对于中压侧目标电压的误差Wi：

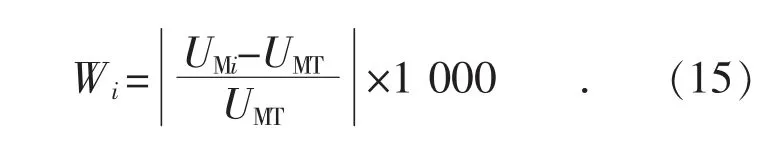
4）步骤四，各档位中压侧实际电压相对于中压侧目标电压的误差Wi最小值对应的档位即为最优档位。当出现2 个档位对应的Wi相同时，应根据档位调整最少原则选择相应档位，例如当前档位为6 档，档位调整范围为7 档和8 档，且7档、8 档相对于中压侧目标电压的误差Wi相同，考虑到选择7 档时，分接开关只需动作一次，而档位选择8 档时，分接开关需动作2 次，因此分接开关档位选择7 档。

5 2 种调压方式及档位选择分析

目前，1 000 kV 特高压变压器主要生产厂家有西安西电、山东电工和特变电工3 家，其中西安西电变压器采用完全补偿方式，山东电工和特变电工变压器采用非完全补偿方式。

采用非完全补偿方式的特高压变压器线圈参数如下：NHV=854，NMV=854，NLV=310，NTV=±45×4，NPV=649，NBV=86，NPV′=460。

采用完全补偿方式的特高压变压器线圈参数如下：NHV=687，NMV=687，NLV=249，NTV=±40×4，NPV=592，NBV=59，NPV′=325。

5.1 2 种调压方式结果分析

5.1.1 高压侧电压UH 保持606.218 kV 不变

当UH为额定值606.218 kV 时，2 种补偿方式对应的三侧电压如表2 和表3 所示。

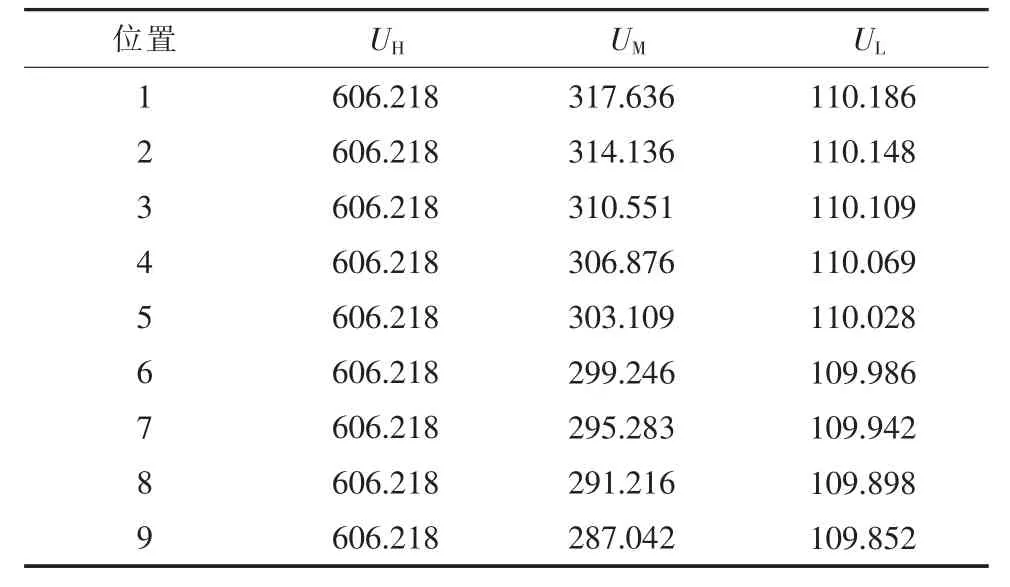
表2 非完全补偿方式对应的三侧电压（UH=606.218 kV）kV

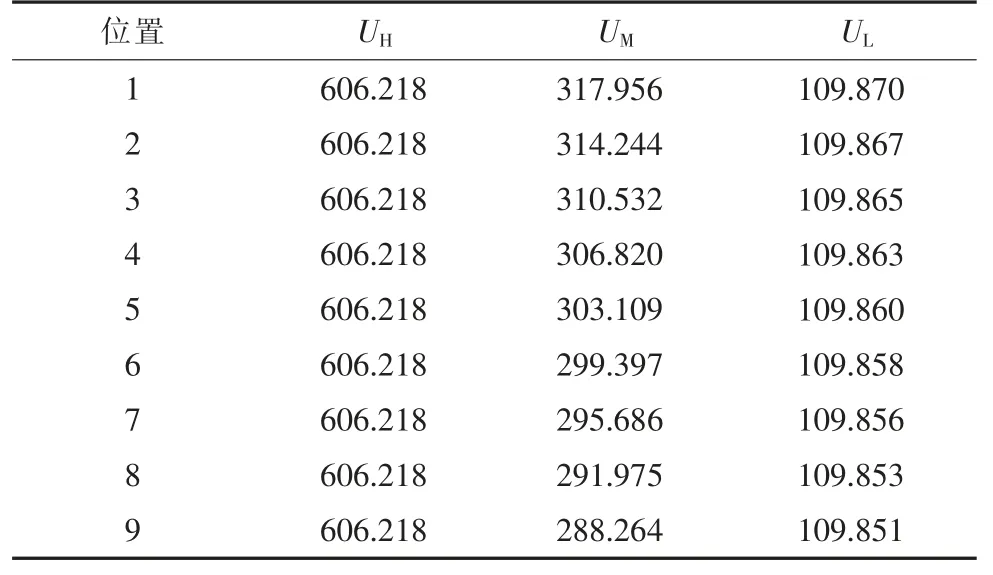
表3 完全补偿方式对应的三侧电压（UH=606.218 kV）kV

1）低压侧波动情况。

图3 为UH=606.218 kV 时低压侧电压，由图可知：相对于低压侧额定电压110 kV，采用非完全补偿方式时，UL在额定值110 kV 两侧波动，平均相对误差为0.871‰；采用完全补偿方式时，UL在额定值110 kV 下侧波动，平均相对误差为1.269‰。因此，采用非完全补偿方式时，UL更加接近额定值110 kV。

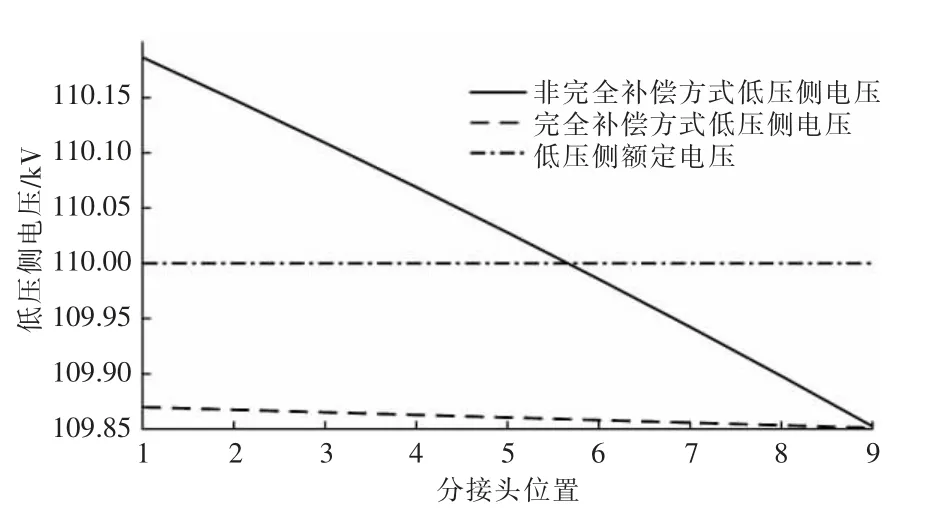
图3 低压侧电压（UH=606.218 kV 时）

相对于低压侧未调档电压（分接头处于5 档），采用非完全补偿方式时，UL随着分接头档位增加而降低，平均相对误差为0.948‰；采用完全补偿方式时，UL随着分接头档位增加而降低，平均相对误差为0.053‰。因此，采用完全补偿方式时，调压过程所产生的低压侧电压波动更小。

2）中压侧调压情况。

随着分接开关档位变化，中压侧额定电压也会发生变化，各档位对应的中压侧额定电压如表4 所示。

表4 各档位对应的中压侧额定电压

图4 为UH=606.218 kV 时UM相对误差。由图4 可知：采用非完全补偿方式时，中压侧调压相对误差随着档位的增加先增加后降低，平均相对误差为1.07‰；采用完全补偿方式时，中压侧调压相对误差也是随着档位的增加先增加后降低，平均相对误差为0.56‰。因此，采用完全补偿方式时，中压侧调压相对误差更小，更加接近中压侧额定电压。

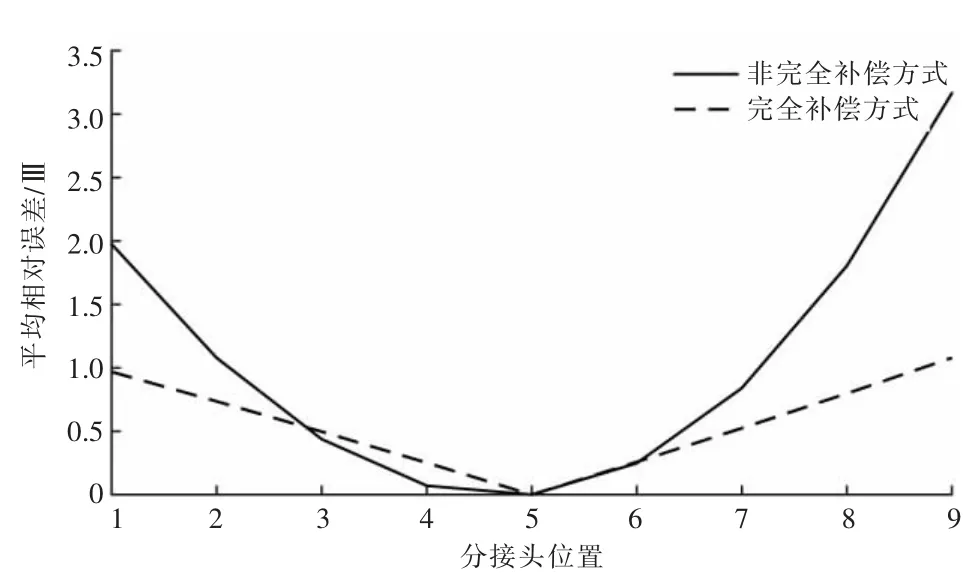
图4 中压侧调压相对误差（UH=606.218 kV 时）

由上述分析可知：当UH=606.218 kV 时，采用完全补偿方式，中压侧调压误差更小，低压电压波动更小；采用非完全补偿方式，低压侧电压更加接近额定值110 kV。因此，特高压变压器采用完全补偿是较好的调压方式。

5.1.2 高压侧电压UH 波动

为分析UH波动时2 种补偿方式的调压结果，文中将研究UH在之间6 档电压所对应的调压结果。

1）低压侧波动情况。

图5 为UH波动时非完全补偿方式低压侧电压，图6 为UH波动时完全补偿方式低压侧电压，显然无论哪种补偿方式，UL都随着分接开关档位的增加而降低，随着UH的增加而升高，符合实际情况，从而验证了式（5）和式（8）的正确性。

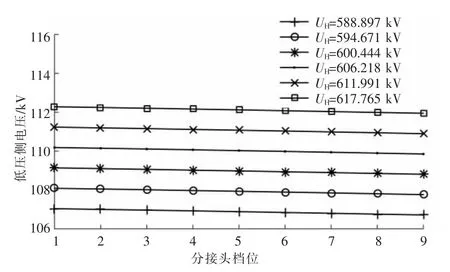
图5 非完全补偿方式低压侧电压（UH 波动）

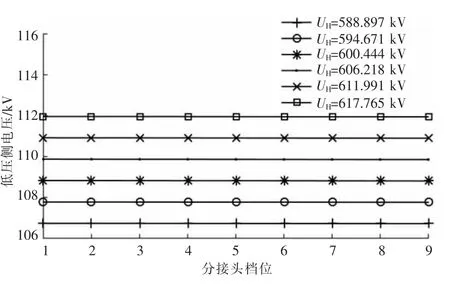
图6 完全补偿方式低压侧电压（UH 波动）

表5 所示为UH波动时2 种补偿方式低压侧电压波动情况。

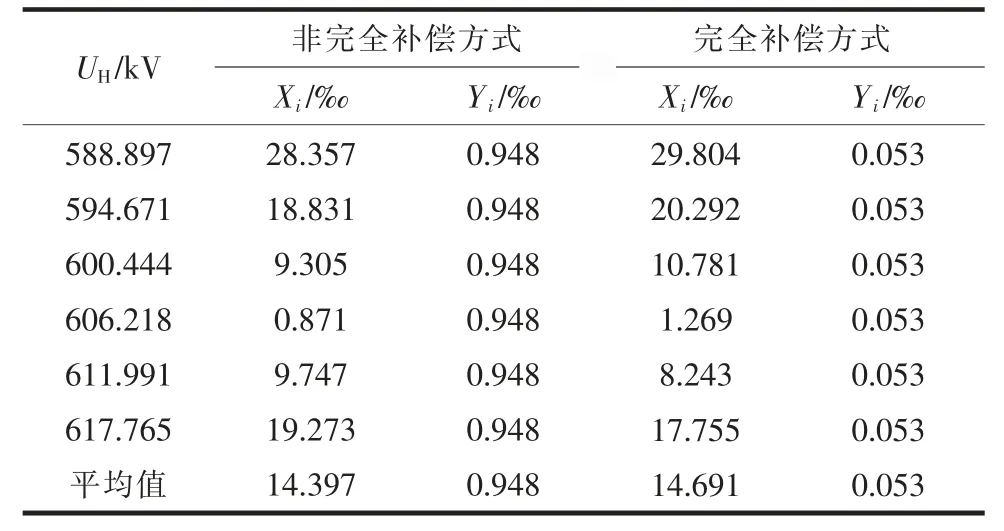
表5 低压侧电压波动率（UH 波动）

分析表5 可知，无论哪种补偿方式，Xi都是随着UH的增加先减少后增加，并在UH为额定值时取得最小值，Yi都与UH无关。对于Xi，采用非完全补偿方式时对应的数值较小，说明采用该补偿方式时，UL更加接近低压侧额定电压；对于Yi，采用完全补偿方式时对应的数值较小，说明采用该补偿方式时，UL波动较小。

2）中压侧调压情况。

图7 为UH波动时非完全补偿方式中压侧电压，图8 为UH波动时完全补偿方式中压侧电压。

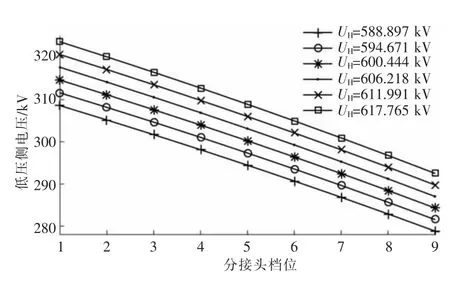
图7 非完全补偿方式中压侧电压（UH 波动）

图8 完全补偿方式中压侧电压（UH 波动）

由图7 和图8 可知，无论哪种补偿方式，UM都随着分接开关档位的增加而降低，随着高压侧电压的增加而升高，符合实际情况，从而也验证了式（5）和式（8）的正确性。

表6 所示为UH波动时2 种补偿方式中压侧电压变化情况。

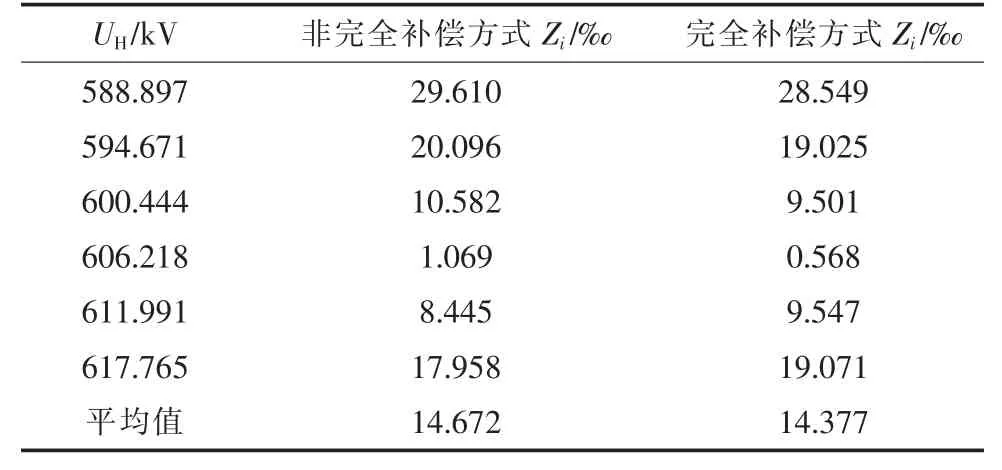
表6 中压侧电压变化率（UH 波动）

由表6 可知，无论哪种补偿方式，Zi都是随着高压侧电压的增加先减少后增加。当高压侧电压UH≥611.991 kV 时，采用非完全补偿方式时对应的Zi数值较小；而当高压侧电压UH≤606.218 kV 时，采用完全补偿方式时对应的Zi数值较小。总体而言，采用完全补偿方式时对应的Zi平均值较小，说明采用完全补偿方式时，UM更加接近中压侧额定电压。

从上文分析可知，不管是UH=606.218 kV，还是UH波动，就中压侧调压和低压侧波动情况而言，都是采用完全补偿方式效果较好。因此，特高压变压器的调压方式宜采用完全补偿方式。

5.2 档位选择方法

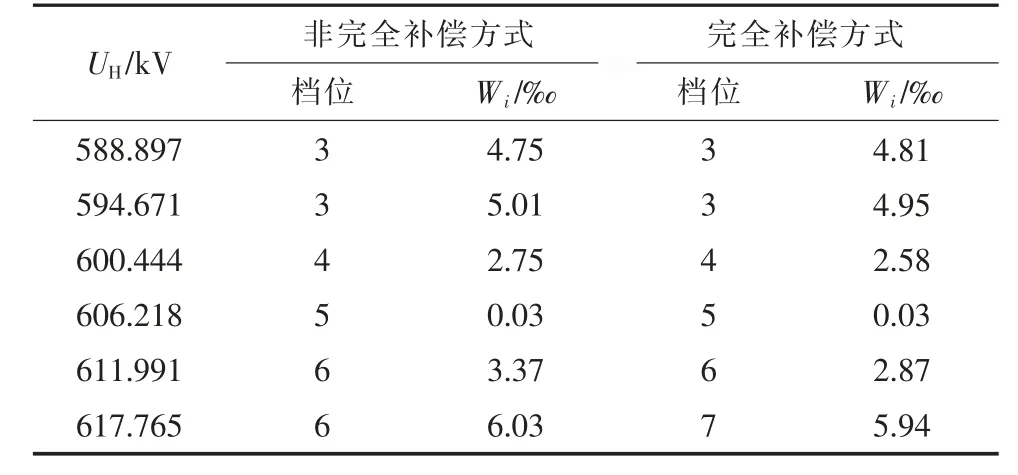
表7 2 种调压方式的档位选择结果

表8 非完全补偿方式高压侧电压与档位对应关系

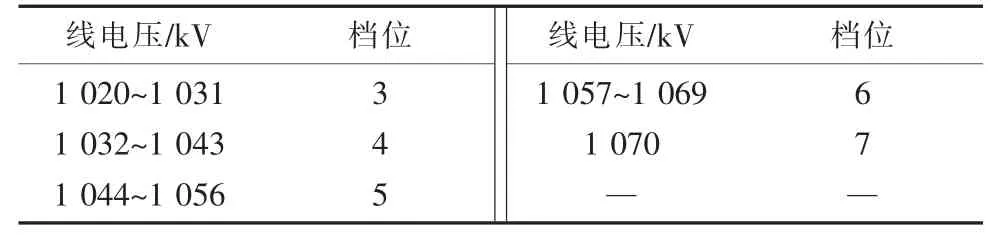
表9 完全补偿方式高压侧电压与档位对应关系

6 结论

1）分析了特高压变压器7 个绕组间的电磁耦合关系，并结合各绕组间的电气联系，以完全补偿方式为例，对特高压变压器的调压过程进行了定性分析。

2）在建立特高压变压器非完全补偿和完全补偿2 种补偿方式数学模型的基础上，从高压侧电压保持额定值和高压侧电压波动2 个方面，对2种补偿方式进行了定量分析，结果表明采用完全补偿方式时，低压侧电压波动更小，中压侧电压调压更准。

3）研究了特高压变压器的档位选择方法，根据一定假设，给出了特高压变压器高压侧电压与档位对应关系，可为现场档位选择提供指导。