基于邻域前向时序最优组合的分布式光伏超短期功率预测

唐雅洁，龚迪阳，倪筹帷，王 波，张雪松，朱 耿

（1.国网浙江省电力有限公司电力科学研究院，杭州 310014；2.国网浙江省电力有限公司宁波供电公司，浙江 宁波 315000）

0 引言

2020 年9 月22 日，习近平总书记在联合国大会上宣布了“二氧化碳排放力争于2030 年前达到峰值，努力争取2060 年前实现碳中和”的中国承诺。在“碳中和”目标下，大力发展光伏等清洁零碳新能源成为碳减排的关键。随着光伏技术不断进步，转化效率不断提升，在光伏补贴下调、光伏电站标杆电价下调、“弃光”现象仍存在的背景下，分布式光伏发电将成为光伏行业发展的重点[1-2]。分布式光伏发电波动性大，对其进行准确功率预测有助于更合理地利用分布式光伏发电产能、增加电网对分布式光伏的消纳能力。

根据电力调度的应用需求，光伏功率超短期预测一般为未来15 min 至4 h 的发电功率预测[3]，对电网调度计划安排及储能系统配置等具有重要意义[4-5]。但目前针对实际投运分布式光伏电站的超短期功率预测方法研究相对较少。在超短期预测时段里，气象要素中的温度、湿度、气压变化并不明显，但云团移动引起的地表辐射变化相对剧烈[6]。这些气象数值需由NWP（数值天气预报）与本地气象站监测仪提供。在具备气象预报计算资源与实地观测设备的情况下，超短期功率预测方法通常根据本地分布式光伏站与气象站所观测数据的实时动态变化来进行预测与修正[7-9]；就方法而言，均以神经网络等机器学习算法为基础，基于大数据分析挖掘光伏功率与各影响因素间的关联性，建立统计预测模型[10-12]。上述方法均综合考虑与分布式光伏站点出力相关的影响因素，但仍面临突发过程性天气下光伏出力波动剧烈时，功率预测偏差较大的问题；同时，大型光伏电站因规模与布局可以配置气象站，而众多小型独立运营的分布式光伏电站，如屋顶光伏站等，往往不具备这种条件，且气象站并非分布式光伏电站的必需配置设施[13]。因此，如何在缺少气象信息的条件下，利用有限的历史数据准确预测分布式光伏功率具有重大意义。

在分布式光伏电站普遍缺乏气象观测信息的条件下，本文基于数据驱动理念，依据邻近区域实时天气的时空关联性，提出了一种基于邻域前向时序最优组合的分布式光伏超短期功率预测方法，不依赖于地表辐照强度等气象观测装置，而从单独实时出力维度进行预测，具有经济、轻量级、易部署的特点。首先，根据本站点经纬度计算地图直线距离，建立邻域站点集合；随后，通过站点前向选择的预测效果校验，逐步建立基于邻域最优组合特征集的超短期功率预测模型。结果表明，本文所提方法在缺乏气象观测信息的条件下，更全面地挖掘了邻域多分布式光伏站点间实时功率的耦合性与联动性，更准确地预测了未来功率变化趋势，有效地提升了超短期预测精度。

1 基于有限信息的分布式光伏超短期功率预测方法

1.1 分布式光伏站点数据概况

当前，许多容量相对较小的分布式光伏电站通常只具备收集历史运行与实时监测出力数据的能力，而基于成本考虑并未配置地面气象站，缺乏站点观测气象数据。此时，NWP 所提供的3 km范围气象预报数据，由于缺乏地面辐照等实际观测信息，在未经实地降尺度修正的情况下将出现较大偏差，难以适用于分布式光伏站点的超短期功率预测；同时，针对每个分布式站点进行基于经纬度的精确气象建模，也需花费较多计算资源和数据存储空间，欠缺经济性与实用性。

因此，对观测设备要求较高、对精细化气象预报依赖性强、基于实时修正关键特征辐照强度值来提升未来时段内预测精度的方法，较难应用于有限信息下的分布式光伏超短期功率预测。

1.2 基于功率时序推移的分布式光伏超短期功率预测

在有限信息下，基于数据挖掘的功率时序推移算法是超短期光伏预测的一种基本方法，主要针对分布式站点收集的历史光伏数据进行趋势学习。由于光伏出力是单变量数据，因此特征主要包括平移特征和时间特征两部分。平移特征指以当前时刻为时间节点，将临近时段内历史光伏出力数据作为特征；时间特征则通常指预测时刻的日历特征，如小时、分钟等。典型分布式光伏站点超短期功率时序预测模型结合两者与光伏出力值间的关系建立点预测模型，如图1 所示。

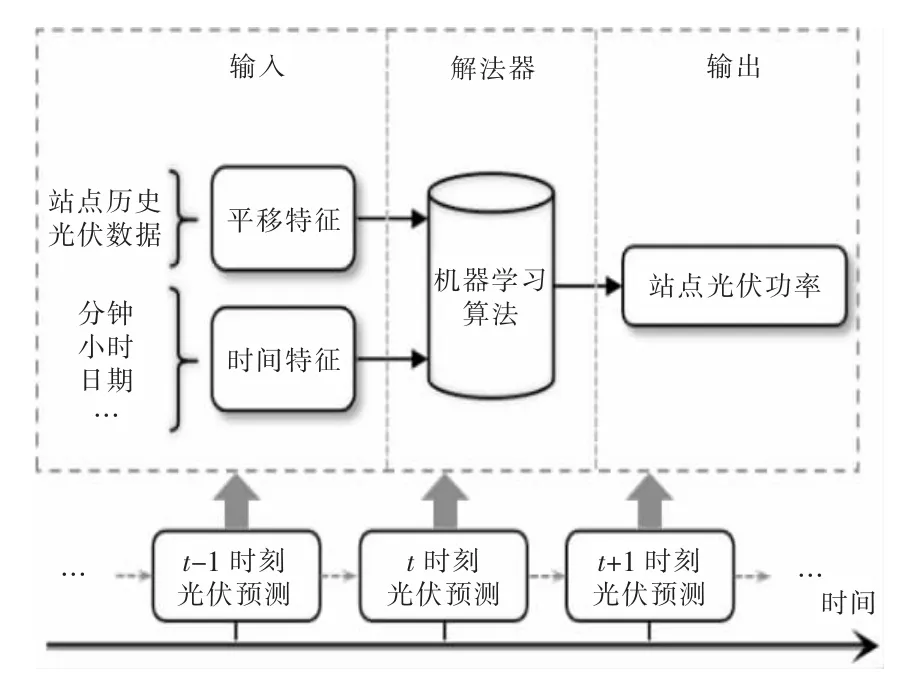
图1 基于功率时序推移的分布式光伏超短期预测模型框架

超短期功率模型预测一般采用滚动计算方法进行，即按照时间顺序计算未来时段内各时刻预测功率，并将已预测时刻作为后续预测时刻的已知信息，直至超短期预测第4 h 的功率预测完成。

1.3 基于多站点相似的分布式光伏超短期功率预测

基于功率时序推移的分布式光伏超短期功率预测方法集中于某一特定地理方位信息，在天气波动下迅速追踪实时气象变化的能力仍有所欠缺。因此，考虑利用多站点信息实现分布式光伏功率预测精度提升。

利用站点功率曲线相似度计算方法，将预测站点邻近区域内站点相似度从高到低进行排序。文献[14]指出，相邻电站的历史功率数据既体现了时间和季节变化趋势，也反映了当地相关气象信息的影响。因此在有限信息下，可采用日曲线归一标准化后的平均欧式距离作为相似度计算标准。站点编号i 与站点编号j 的相似度Sij计算公式如下：

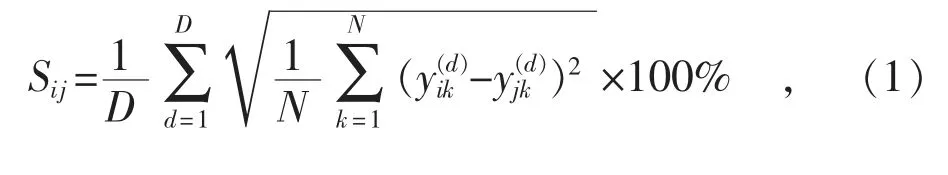
由式（1）计算得出所有站点与预测站点功率的平均相似度，选取相似度较高的邻近站点增加本站点预测模型输入特征维度，进行更为复杂的功率时序建模，如图2 所示。然而，出力相似度较高的站点所处地理气象状态通常也相似，因此在组合预测上易出现信息重复利用、组合扩展有效增维信息较少的问题，预测精度提升受限。

图2 基于多站点相似的分布式光伏超短期预测模型框架

2 基于邻域前向时序最优组合的分布式光伏超短期功率预测方法

2.1 组合模型评价指标

预测模型训练样本的评价指标通过K 折交叉验证求取。K 折交叉验证法将训练样本划分为大小相同的K 个分区，依次选择不同分区作为测试集，剩余的K-1 个区作为训练集。每次训练误差为预测值与真实值间的MAPE（平均百分比误差），记为JMAPE，最终误差为所有训练误差的平均值公式如下：

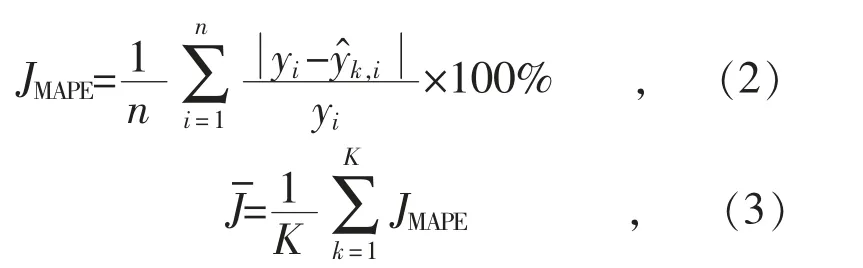
式中：n 为测试区样本个数；yi为光伏功率实际值；为第k 次交叉检验的光伏功率预测值。

2.2 序列前向选择法

SFS（序列前向选择法）是一种链式贪心算法，也是一种常用的特征选择方法。SFS 算法从空集开始，每次从未选择特征集中选择一个使学习器训练的评价函数J（X）最好的最优特征k，加入最终选择特征集X；当J（X）无法取得更优时，前向选择结束。

基于SFS 框架，在典型站点功率时序推移与多站点预测模型基础上，本文提出优化组合邻域站点实时功率信息的建模方法，利用SFS 对邻域站点进行筛选与校验，扩展观测维度，深入挖掘区域实时气象的延续变化反映在邻近分布式光伏电站出力上的关联耦合性，进一步提升本站点预测精度。

2.3 基于邻域前向时序最优组合的分布式光伏超短期功率预测

2.3.1 邻域站点集合构建

对于分布式光伏站点A0，根据强对流云团较快移动速度一般为60 km/h、超短期预测时间尺度为未来4 h，计算可得与A0站点直线距离240 km（距离计算时海拔忽略不计，下同）以内的云团可能在预测时段内移动至站点位置，带来超短期预测时段内地理气象变化的延续性。因此分布式光伏站点A0的邻域可设定为与A0距离不大于240 km 的其他站点。假设A0站点的经纬度为（x0，y0），地图上另一站点Ai的经纬度为（xi，yi），则两站点之间的直线距离计算公式如下：

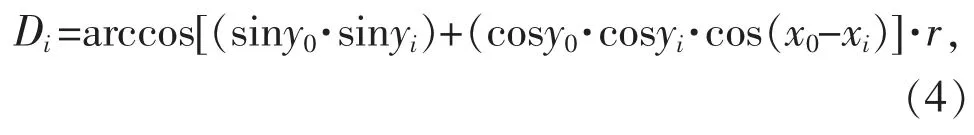
式中：Di为站点A0与站点Ai之间的直线距离；r为地球平均半径；所有变量单位均为km。

计算得到所有满足影响距离要求的站点集合为邻域站点集合S，表达式如下：

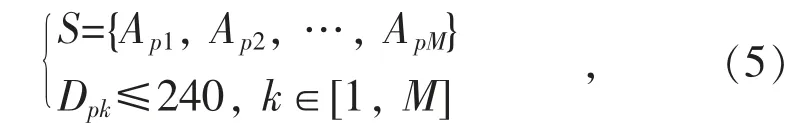
式中：M 为邻域站点个数；Pk为站点编号。

2.3.2 基于邻域前向时序最优组合的分布式光伏超短期光伏功率预测

令站点A0由以下步骤一计算所得邻域站点集合为{A1，A2，…，AN}，已选择最优邻域站点组合集为V，最优输入特征集为X，待校验邻域站点集为S，最优误差校验值为e，采用迭代扩展校验的方法选择邻域前向时序最优组合序列。具体步骤如下：

1）步骤一，迭代初始化。i=0，V（0）=X（0）=∅，S（0）={A1，A2，…，AN}，e（0）=+∞。

2）步骤二，迭代建模。设当前已迭代至第i次，1≤i≤N，则上一次迭代已选择邻域站点组合集为V（i-1），输入特征集为X（i-1），可选择邻域站点集为S（i-1），则本轮可扩展新增站点为S（i-1）中所有待校验择优站点Ak（Ak∈S（i-1）），遍历S（i-1）并枚举本次迭代的邻域站点组合集V′如下：

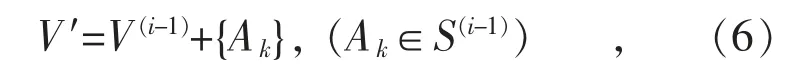
以预测时刻光伏功率作为输出Y，枚举集合V′内所有站点的最优共同平移输入特征集时段长度L′，结合预测时刻的时间平移特征向量，包含{分钟，小时，日，月，季度，年}，可得到预测时刻待校验的多维输入特征向量集XV′如公式（7）所示。

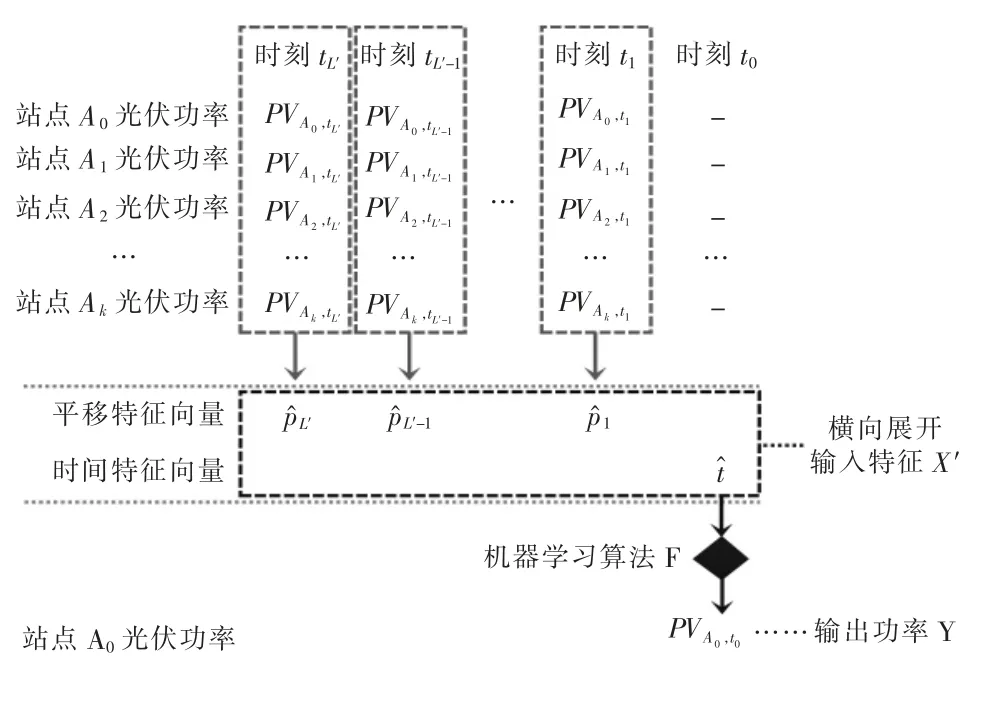
图3 基于邻域前向时序最优组合的分布式光伏超短期功率预测模型框架

3）步骤三，迭代校验。采用机器学习算法，对待校验模型训练样本进行K 折交叉验证。在该验证下，枚举每个待校验站点组合集V′下的时段长度L′，并计算每次输入特征集X（V′）模型的误差均值。令最优误差均值为e′=min（（V′）），最优误差所对应的邻域站点集为Vmin，特征集为Xmin，此时在V′中迭代新加入的邻域站点为AkS。

4）步骤四，迭代终止判定。若e（i）≤e（i-1），则令V（i）=Vmin，X（i）=Xmin，S（i）=S（i-1）-{AkS}，i=i+1，否则迭代终止；再判定若i=N+1，则算法结束。此时，迭代有效次数M=i-1。

通过上述步骤，算法终止后得到的V（M）即为对站点A0进行邻域选择后的最优站点集合，对应的X（M）即为模型输入特征集。令最后一次有效迭代过程中计算得出的最优时段长度为L，则基于邻域前向时序最优组合的超短期光伏功率预测模型如表1 所示。

表1 基于邻域前向时序最优组合的超短期光伏功率预测模型数据结构

3 实验及结果分析

3.1 实验数据集描述

实验平台条件为Windows10 X64 操作系统、Intel i5-7 500 CPU，使用Python 语言。实验以浙江宁波某区域分布式光伏系统为对象，共包含24 个光伏站点，如图4 所示。

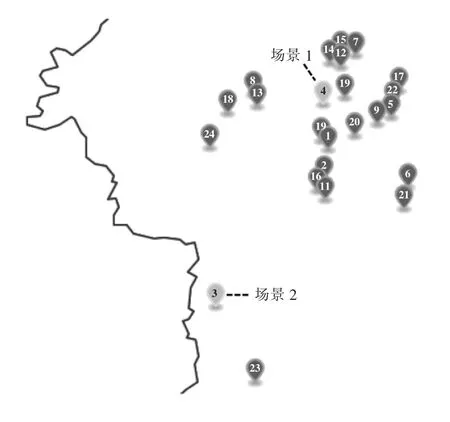
图4 浙江宁波某区域分布式光伏系统站点

其中，站点经纬度与光伏功率数据已知，功率实测数据为现场光伏板采集，时间分辨率一致，均为2020-04-01—2021-05-09，每15 min一个数据点，每天共96 组。

为了验证本方法在典型天气下的超短期预测效果，以2020-04-01—2021-05-07 的数据作为训练样本，2021-05-08—2021-05-09 作为测试样本，在邻域站点较密集的场景1 与邻域站点较稀疏的场景2 下进行对比。为实现合理对比，各模型均采用XGBoost[15-16]方法，参数保持一致，关键参数包括：树深度7，学习率0.01，树数目1 000。因数值缩放不影响树分类模型分裂点位置，XGBoost 模型采用原始数据进行计算。同时，One-Hot 编码[17]并不完全适合树分类模型，其可能的不平衡切分增益会导致数据被切分到零碎的小空间上，使学习效果变差。因此，本文对非连续时间特征采用离散标签化处理。

3.2 评估指标

本文选取测试集所有超短期预测第4 小时预测点的MAPE 作为超短期功率预测模型性能的评估指标，公式如下：

式中：yt为每次超短期预测的第4 小时实际光伏发电数据；为每次超短期预测的第4小时预测光伏发电数据；T 为数据总量。

3.3 结果分析

为了验证本文方法的预测效果，考虑场景1邻域站点较密集与场景2 邻域站点较稀疏下的分布式光伏站点超短期功率预测精度。

首先根据2.3.2 步骤一计算可得，该区域内所有站点均在邻域范围内。各预测模型扩展构建过程及其计算结果对比如表2 所示。

表2 展示了本文所提方法、基于功率时序推移、基于多站点相似的超短期功率预测模型预测效果对比。其中，基于单站点功率时序推移模型即为仅有该站点功率特征时的邻域前向时序最优组合预测模型；而基于多站点相似模型则选取与本文方法最优组合站点个数相同的几个相似度最高站点进行建模，实现站点组合选择方法的对比。

由表2 可知，各测试场景均依据邻域站点集增加的特征维度，逐步提升了预测精度。场景1下本模型预测精度分别提升了1.06%与1.01%；场景2 下本模型预测精度分别提升了1.58%与1.04%，预测曲线对比如图5、图6 所示。由图可看出，本方法搭建的模型预测曲线在多云天气象频繁变化时对实际出力趋势跟随性更强，在晴天实际出力平稳时毛刺较少，在2 种典型气象场景下均能取得最好预测效果。分析其原因在于：

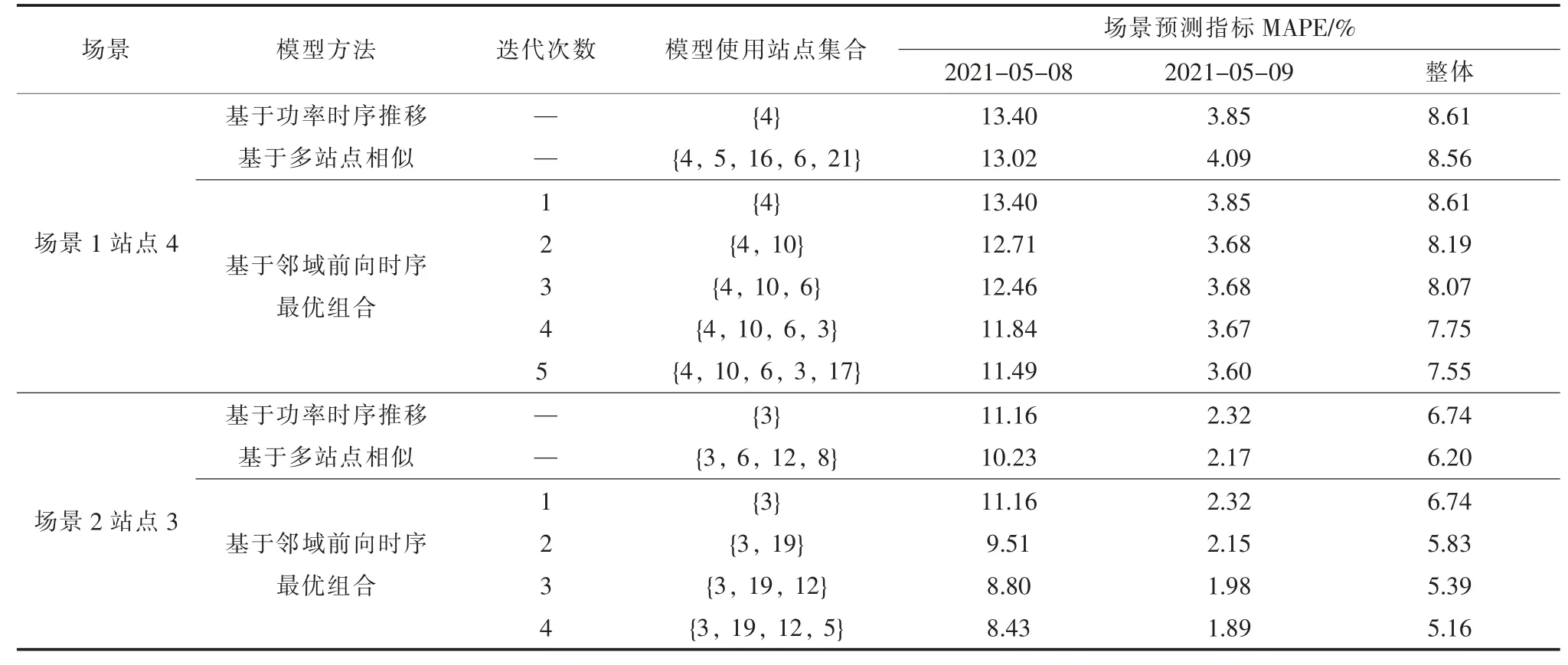
表2 超短期光伏功率预测模型计算结果对比

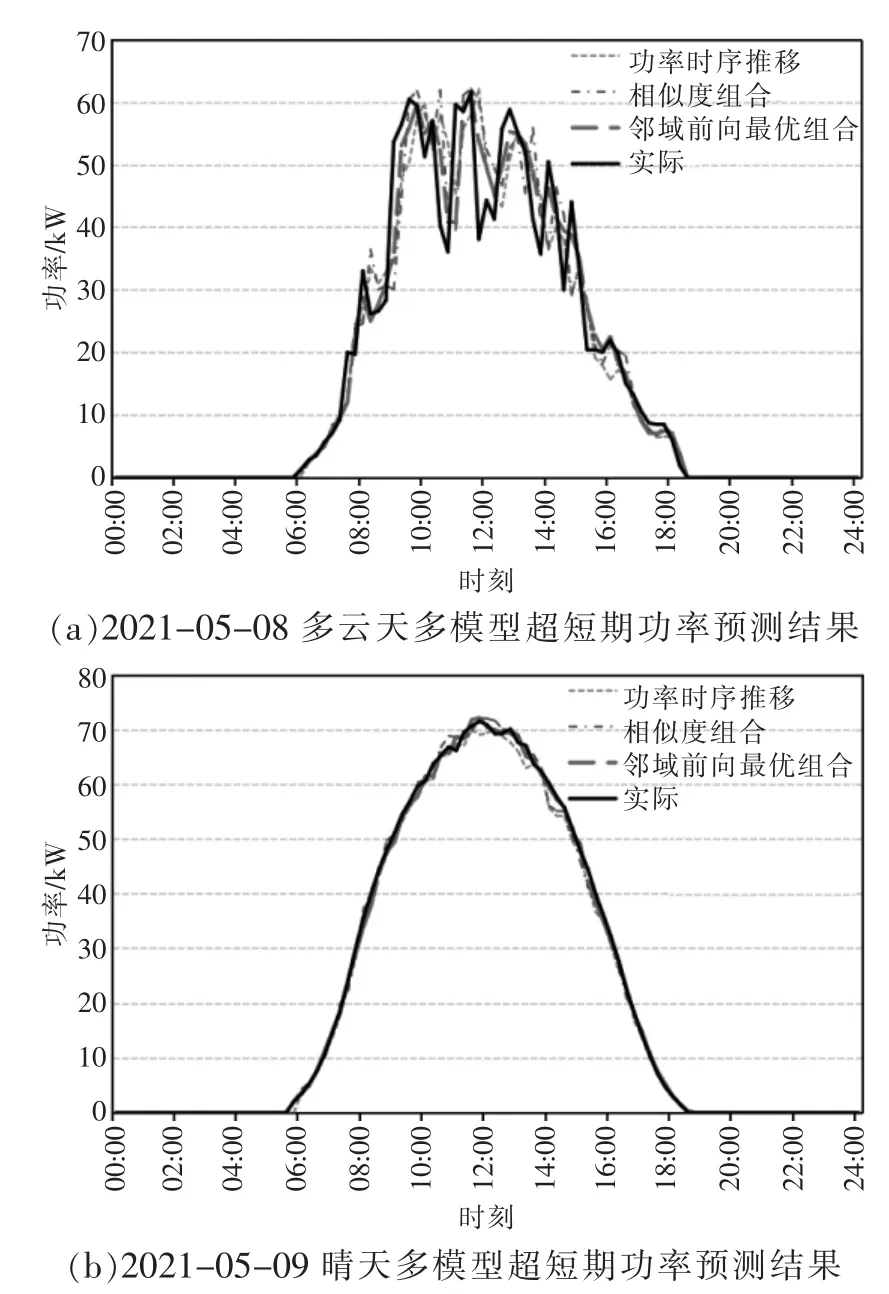
图5 场景1 下的超短期功率预测结果对比

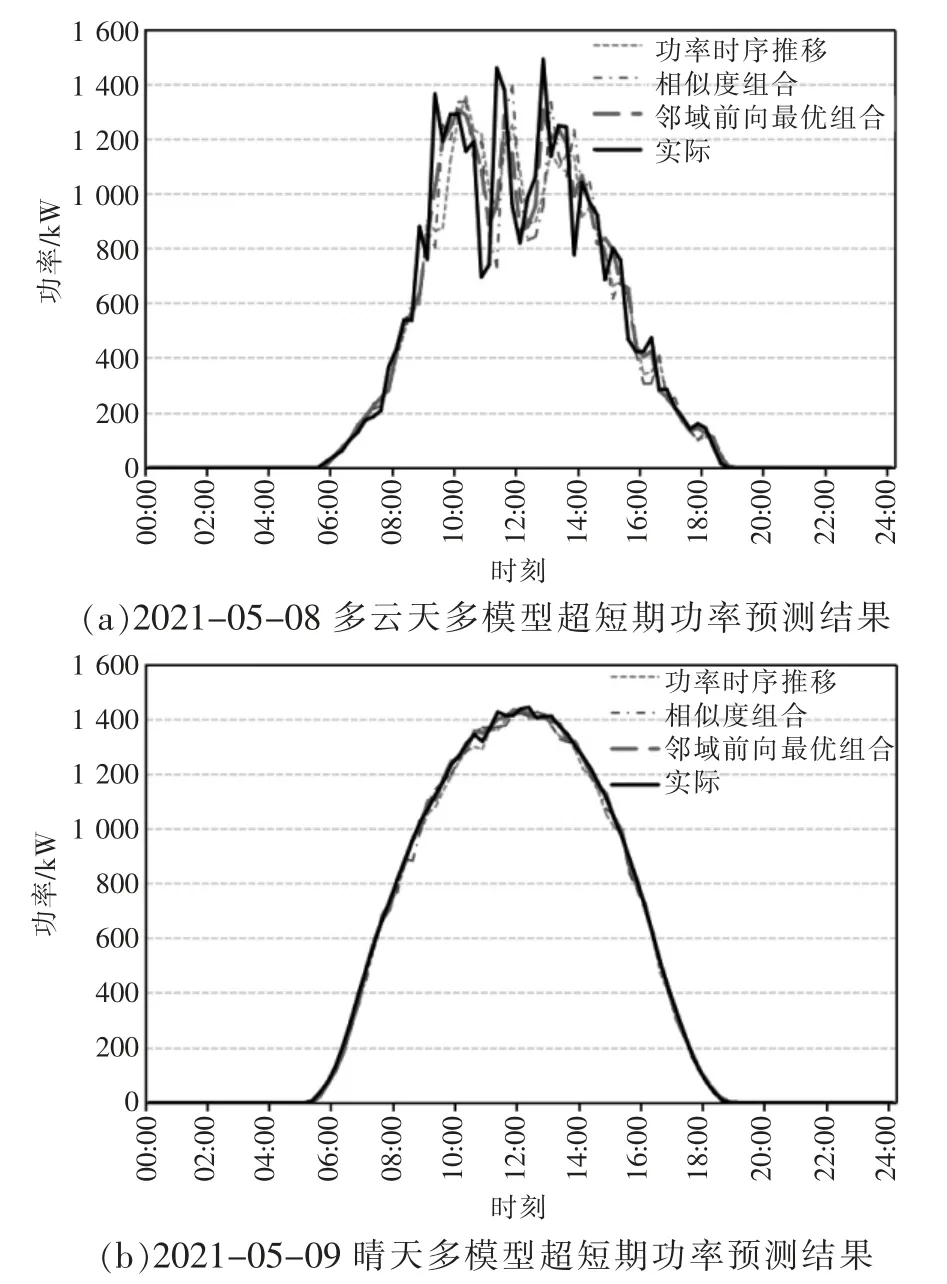
图6 场景2 下的超短期功率预测结果对比

1）邻域站点组合扩展了预测输入特征维度，充分反映了实时气象延续性对邻域中分布式光伏站点出力间时空耦合关联性的影响，并基于对多站点复杂出力特性的综合训练，实现了精细化预测模型搭建。

2）邻域前向时序最优选择更可靠、全面地挖掘了多站点实时功率的互动性，通过机器学习算法嵌入式枚举与多重训练校验，较基于指标阈值的过滤式特征选择方法（如相似度排序）具备更强的预测性能。

此外，并非所有邻域站点均对本站点的预测效果有提升作用，主要有如下原因：一是现实地理因素的影响，例如山脉阻隔云团移动等，导致两位置站点的气象延续性不强，因而分布式光伏出力的关联性随之较弱；二是部分邻域站点对本站点出力的影响因子在已选定站点集合中已有体现，而扩展的特征维度冗余，导致模型的泛化性下降。

综上所述，在不依赖气象站观测装置的情况下，仍可从气象变化的时空延续性角度，挖掘邻域站点功率的关联耦合性，最大化整合与利用有限观测信息，提升站点的超短期预测精度。

4 结论

考虑分布式光伏站点存在无地面气象观测站配置的情况，本文提出一种基于邻域前向时序最优组合的分布式光伏超短期功率预测方法，分析对比了多场景下多模型的预测效果。结果表明：

1）邻域站点间功率组合预测方法，不依赖于地面气象站等观测装置，充分挖掘了由区域气象时空推移影响的分布式光伏站点出力间的关联性，利用基于时空耦合的预测输入特征维度扩展，简洁高效地提高了超短期光伏预测精度。

2）前向时序最优组合方法，通过枚举与多重训练校验，更可靠、全面地挖掘了多邻域分布式光伏站点间实时功率的耦合性与联动性，有效避免了根据相似度排序组合易出现的信息重复利用、组合扩展有效增维信息较少的问题，提升了预测性能。

3）通过实验数据集验证了模型在典型天气下的预测效果，并通过对比实验全面考量本文算法的预测性能，降低了实验的偶然性，增强了实验结果的可参考性。

在后续研究中，可搭建符合不同天气场景的组合预测方法，进一步提升预测准确度。