频响函数二次正交法在Davenport风速谱下结构系列响应简明封闭解的应用研究

葛新广, 张梦丹， 龚景海， 李创第,

(1.上海交通大学 船舶海洋与建筑工程学院，上海 200240；2.广西科技大学 土木建筑学院，广西 柳州 545006)

随着建筑结构分析能力和建造水平的不断提高，建筑结构向高、轻、柔方向发展，从而导致高层建筑对风的敏感性十分突出。此外，随着自然环境的不断恶化，各类极端天气的发生都伴随着破坏性强风出现，因此，建筑结构的抗风研究至关重要。大量的研究表明[1-2]，强风对建筑物的振动作用是由短周期的脉动风所引起的。工程上研究强风对结构的影响有风洞试验方法[3-4]、CFD模拟[5-6]和随机风振理论法[7-8]三种方法。其中，风洞试验方法结果较为准确，但试验成本较高，常采用缩尺模型试验获得风荷载体型系数之后采用理论方法对建筑结构进行风振响应分析。CFD方法是通过数值手段模拟结构物的绕流场并考虑流固耦合作用的一种结构风振响应分析方法，但模拟时对计算机要求较高，且耗时久，分析精度受数学模型的选择控制。而随机风振理论法，则是将强风作为结构分析的荷载，利用风的功率谱概念来表述脉动风的动力作用。对于建筑结构而言，该方法基本能满足工程精度要求，且具有计算分析相对简单、能与建筑结构恒载、其他活载进行作用效应组合以便于工程设计的特点。Davenport及李创弟等分别提出了随机风速谱，其中Davenport风速谱应用最为广泛，成为各国建筑风荷载取值的依据。

随机风振响应的分析方法主要有频域法[9-12]和时域法[13]。频域法中结构响应的功率谱可表示为结构的频响函数与风激励功率谱的乘积，表达式简洁明了。频域法的典型方法为传递函数法和虚拟激励法。李创第等利用传递函数法研究了巴斯金谱激励下的黏弹性耗能结构的风振响应，但其结构的响应等效为振子的二阶振动方程基于巴斯金谱风速谱下的响应，所得结构响应方差的表达式较为复杂。张文首等[14]基于虚拟激励法研究了基于Davenport风速谱激励下的结构响应功率谱，研究表明虚拟激励法所获得的结构风振响应为CQC(完全平方法)解，但结构响应谱矩(方差)分析时需要数值积分，积分精度和运算效率受积分区间和积分间距影响。赵中伟等[15]利用本特征-虚拟激励法研究了大跨度钢结构基于Kaimal谱下的施工过程中的风振响应，研究表明，虚拟激励法可高效获得结构风振响应功率谱，但存在需要数值积分响应方差的问题。时域法中，结构响应的协方差表示为结构脉冲函数与激励协方差的二重积分，而Davenport风速谱无协方差，故时域法在分析风振响应时需要转为频域法进行求解。曹宏等利用实模态解耦法给出了经典阻尼结构基于Davenport谱下的风振响应的解析解；邹万杰等[16]利用复模态法研究了非经典阻尼结构基于Davenport谱下的风振响应的解析解，推广了曹宏等的方法的应用范围。时域法所得结构风振响应的0阶、2阶及4阶谱矩表达式较为复杂，不利于工程应用。

针对上述既有方法的不足，本文首次提出了结构频响函数二次正交法，并成功获得了结构基于Davenport风速谱激励下系列响应(结构层绝对位移及其振动速度、层间位移及其变化率)0-2阶谱矩及4阶谱矩的简明封闭解。首先，利用给出考虑竖向空间相关性的脉动风压功率谱密度函数的简明表达式；其次，综合应用复模态法和虚拟激励法获得结构风振响应(结构层绝对位移及其振动速度、层间位移及其变化率)的二次正交功率谱密度函数的简明表达式；最后，根据随机振动理论中谱矩的定义，获得了结构风振响应的0阶、1阶、2阶及4阶的谱矩的简明封闭解。

1 风压力功率谱

脉动风是引起建筑结构振动的关键因素，建筑结构在风荷载作用下的脉动风压力表示为

pf(Hi,t)=I0(Hi)B(Hi)u(t)

(1)

式中：pf(Hi,t)为离地Hi高度处的脉动风压力值；I0(Hi)是方差为1的随机变量，其表示脉动风压的空间相关性；u(t)为风速谱。B(Hi)为风压力强度系数

(2)

式中：Ai,μs(Hi)、μz(Hi)、w0分别为离地高度为Hi的迎风面积、风荷载体型系数、风压高度变化系数和基本风压值；Kr为与地面粗糙度有关的系数。

Davenport风速谱有着广泛工程应用，其功率谱密度函数

(3)

由于任意两质点所受的脉动风压力不可能同时达到最大值,须考虑空间位置的相关性，则考虑空间相关性的平稳脉动风压pf(Hi,t)和pf(Hj,t)的协方差

CPf(Hi,Hj,τ)=E[pf(Hi,t)pf(Hj,t+τ)]=

B(Hi)B(Hj)E[I0(Hi)I0(Hj)]Cu(τ)

(4)

式中：

(5)

令：

(6)

则考虑空间相关性后的风压协方差为

CPf(Hi,Hj,τ)=ρijCu(τ)

(7)

由Wiener-Khinchin定律，考虑空间相关性的风压功率谱为：

(8)

把式(7)代入式(8)，考虑空间相关性的风压功率谱与Davenport风速谱存在简明关系

SPf(Hi,Hj,ω)=ρijSu(ω)

(9)

2 结构系列响应的频响函数的二次正交法

建筑结构在脉动风荷载Pf作用下的运动方程为

(10)

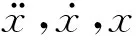
风对结构的作用常取前m振型，设

x=φmq

(11)

式中：φm为结构前m振型，其为m×n矩阵;q为第广义坐标向量，q=[q1…qm]T，“T”为向量的转置。

把式(11)代入式(10)并由式(10)与实模态的正交性，结构的振动方程改写为

(12)

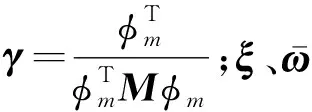
引入状态变量

(13)

则式(10)改写为

(14)

其中：O2为m×m矩阵，其元素均为0；E1为m×m的单位对角矩阵。

根据复模态法理论，式(14)存在左、右特征向量V、U和特征值矩阵P使之解耦，即存在如下关系

(15)

式中，特征值矩阵P为对角阵，其元素的实部为负实数。

引入复模态变换

y=Uz

(16)

由复模态理论，式(14)改写为

(17)

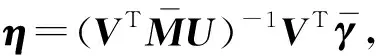
由于P为对角阵，式(17)的分量形式

(18)

式中：ηk表示η矩阵第k行的元素。

根据虚拟激励法，并由式(9)风压谱与风速谱的关系，则式(18)的频域解

(19)

由式(11)、(13)和(16)，则结构响应的频域解

(20a)

(20b)

(20c)

(20d)

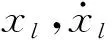
从式(20)可知，结构响应的位移及速度可统一表示为

(21)

由虚拟激励法，则Dl的功率谱为

(22)

针对式(22)可获得其更为简洁的表达式

SDl(ω)=HDl(ω)Su(ω)

(23)

式中,HDl(ω)为结构的频域响应函数，其的正交化形式为

(24)

式(24)的具体推导过程见附录A。

由式(23)可知，结构基于Davenport风速谱系列响应功率谱等于结构的频响函数与风速谱的简单乘积。由式(24)可知，结构响应的频响函数可表示为结构振动复特征值pi(i=1～2m)与频域变量ω平方和的线性组合，具有正交性的特征，故称之为频响函数的二次正交化。所获得频响函数为显示解，且具有简洁性，为后文获得结构响应谱矩和方差的简明封闭解奠定基础。

3 结构风振响应谱矩的简明封闭解法

根据随机振动理论，随机激励下线性结构位移/层间位移的0阶谱矩等于位移/层间位移的方差。位移/层间位移的2阶谱矩等于速度/层间位移变化率的0阶谱矩，等于速度/层间位移变化率的方差。位移的4阶谱矩等于速度的2阶谱矩，等于加速度的0阶谱矩，即速度的2阶谱矩等于加速度的方差。结构振动加速度是建筑舒适度[17-18]分析的基础；位移/层间位移响应的1阶谱矩是动力可靠度[19]谱参数分析的重要参数之一。为此需要对结构风振响应的0-2阶谱矩和4阶谱矩进行分析。

根据随机振动原理，结构响应的谱矩定义

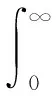
(25)

3.1 结构响应0-2阶谱矩的简明封闭解

把式(23)代入式(25)

统计学处理 采用SPSS 23.0、Stata 14.0统计软件对数据进行处理。通过SPSS 23.0对数据进行描述分析，将数值变量转化为分类变量，通过单因素方差分析和卡方检验，比较不同年份研究对象年龄、性别及发病率的差异性。采用单因素分析和卡方检验分析研究对象在开放式队列中哮喘发病的影响因素。由于本研究发生哮喘结局的研究对象人数所占总的观察对象比例较小，因此，多因素分析采用适用于罕见结局发生率的多因素Poisson回归模型，使用Stata 14.0统计学软件建立多因素Poisson回归模型，将哮喘发生结局作为被解释变量纳入Poisson回归模型中，该模型设定P<0.05具有统计学意义。

(26)

式中：Χk,q的计算见附录B

(27)

对式(27)当q=0，2时进行积分得

(28a)

(28b)

对式(26)，当q=1时进行积分，得：

(29)

3.2 风振加速度方差的简明封闭解

由随机振动理论，风振加速度方差等于风振绝对位移变化率的2阶谱矩，故由式(28b)可获得结构振动的加速度的方差

(30)

4 算 例

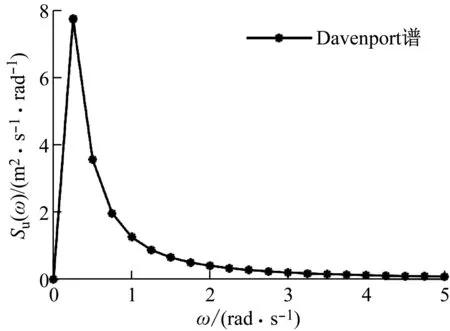
图1 Davenport风速功率谱Fig.1 Speed PDF of Davenport

4.1 本文方法验证

4.1.1 结构系列响应功率谱对比分析

为验证本文方法中结构频响函数二次正交化的正确性，就结构系列响应的功率谱密度函数利用本文方法与传统虚拟激励法进行对比分析，如图2和3所示。从图中可知，本文方法与传统虚拟激励法的结构响应功率谱密度函数完全吻合，从而说明结构频响函数二次正交化法的正确性。由于传统方法的功率谱表达式为式(22)，而本文方法的功率谱表达式为式(23)，故本文方法的功率谱更为简洁。

4.1.2 系列响应谱矩的对比分析

为验证本文所获得的结构风振系列响应0-2阶谱矩及加速度方差的正确性，与虚拟激励法进行对比分析。由于虚拟激励法分析结构响应谱矩和方差时受积分步长和积分区间的影响较大，积分区间上限暂定1 000 rad/s,积分步长取3种，具体如图4～8所示。由图可知，随着积分步长的减少，虚拟激励法所得谱矩与本文方法越来越接近，说明本文方法的正确性。同时说明，虚拟激励法在分析随机响应谱矩时积分步长的选择对于响应精度非常重要。

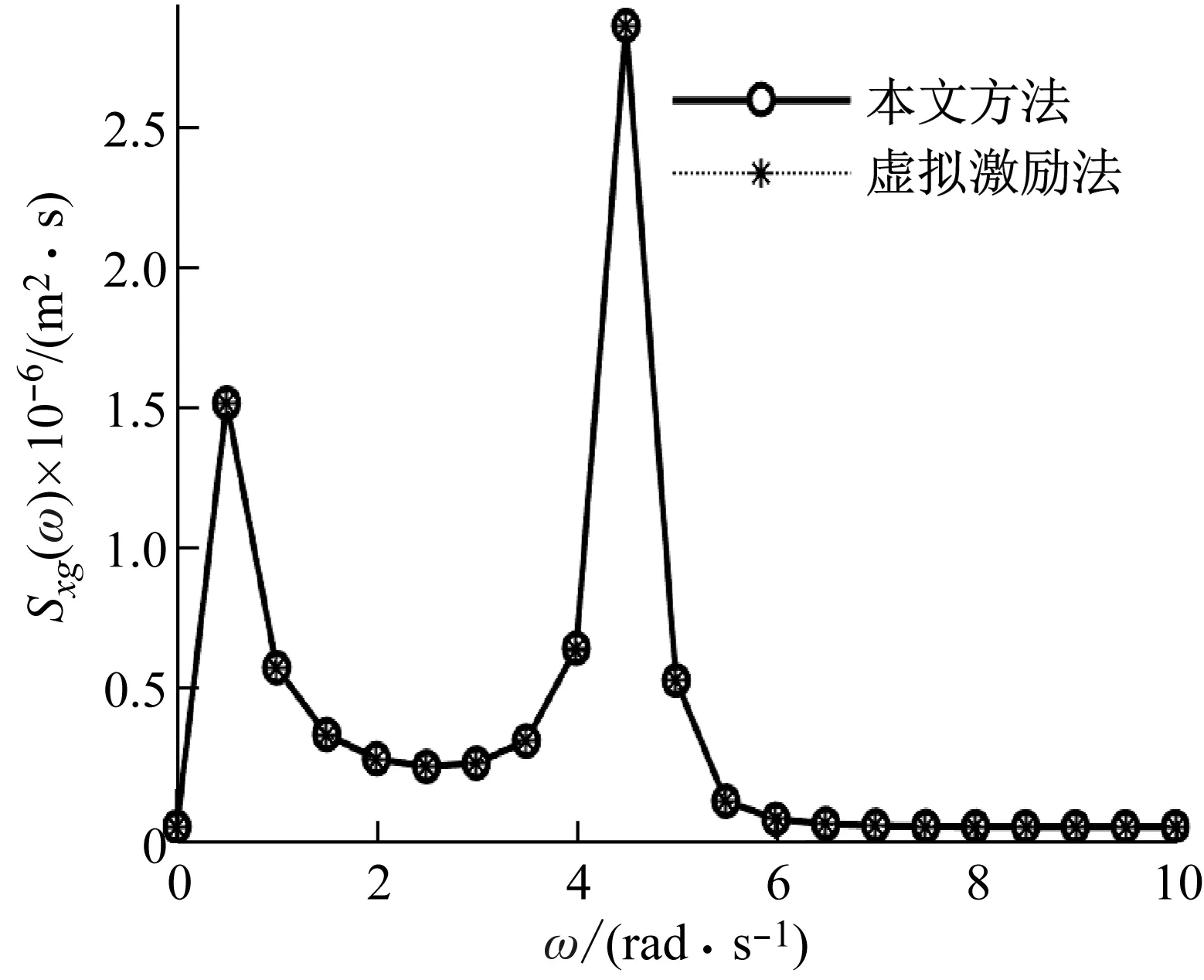
图2 第1层位移功率谱对比图

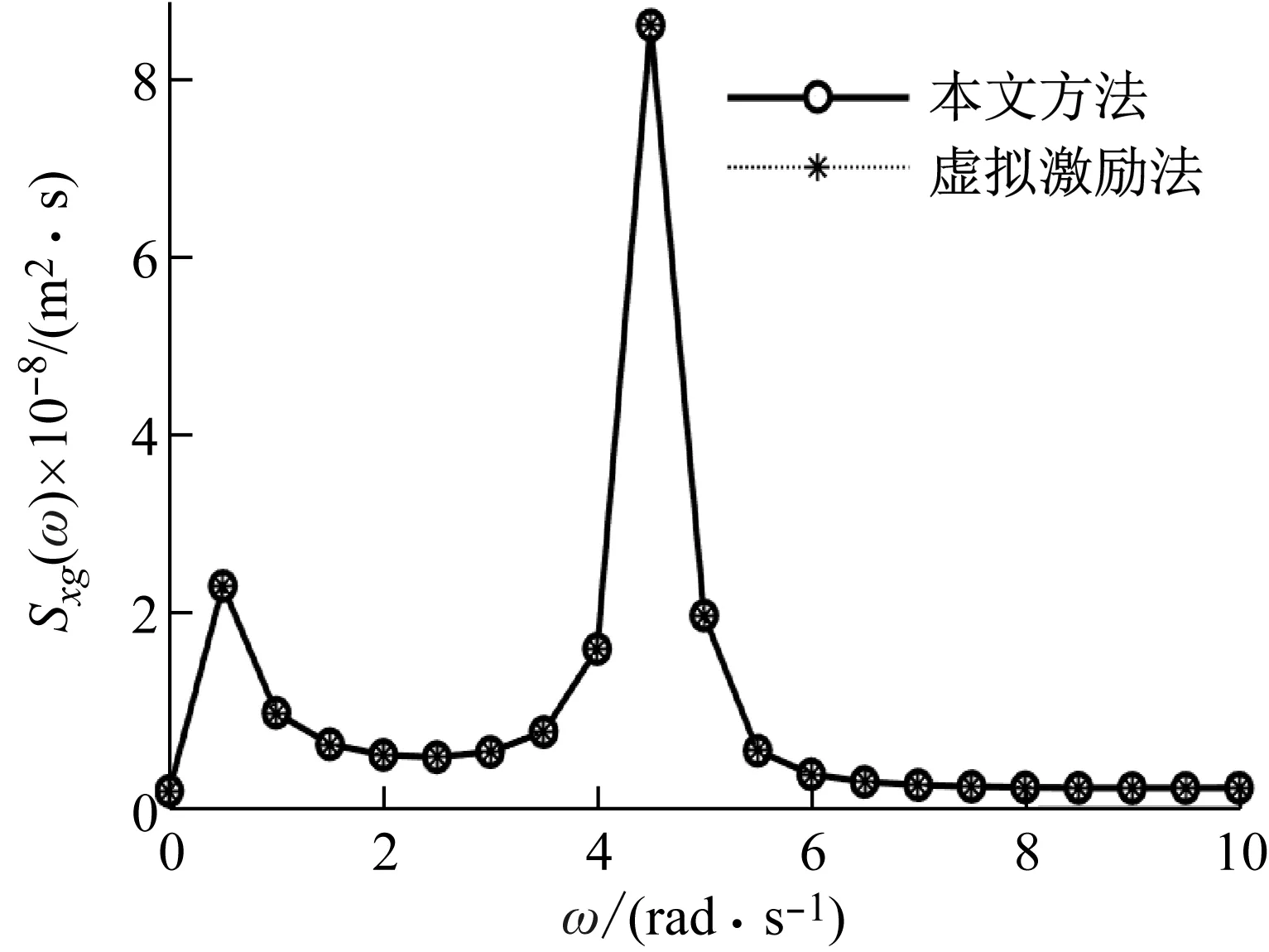
图3 第10层层间位移功率谱对比图Fig.3 Comparison of PDF of interlayer displacement of10th floor

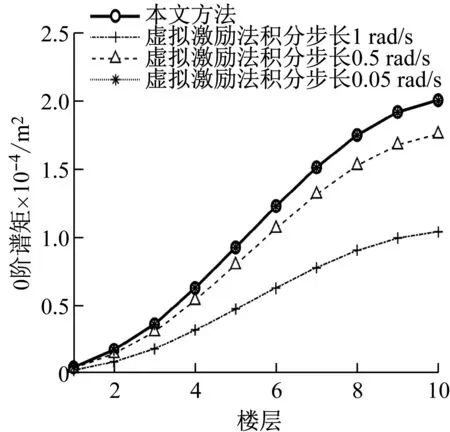
图4 位移0阶谱矩对比图Fig.4 Comparison diagram of 0 orderspectral moment of displacement

图5 位移1阶谱矩对比图Fig.5 Comparison diagram of 1st orderspectral moment of displacement

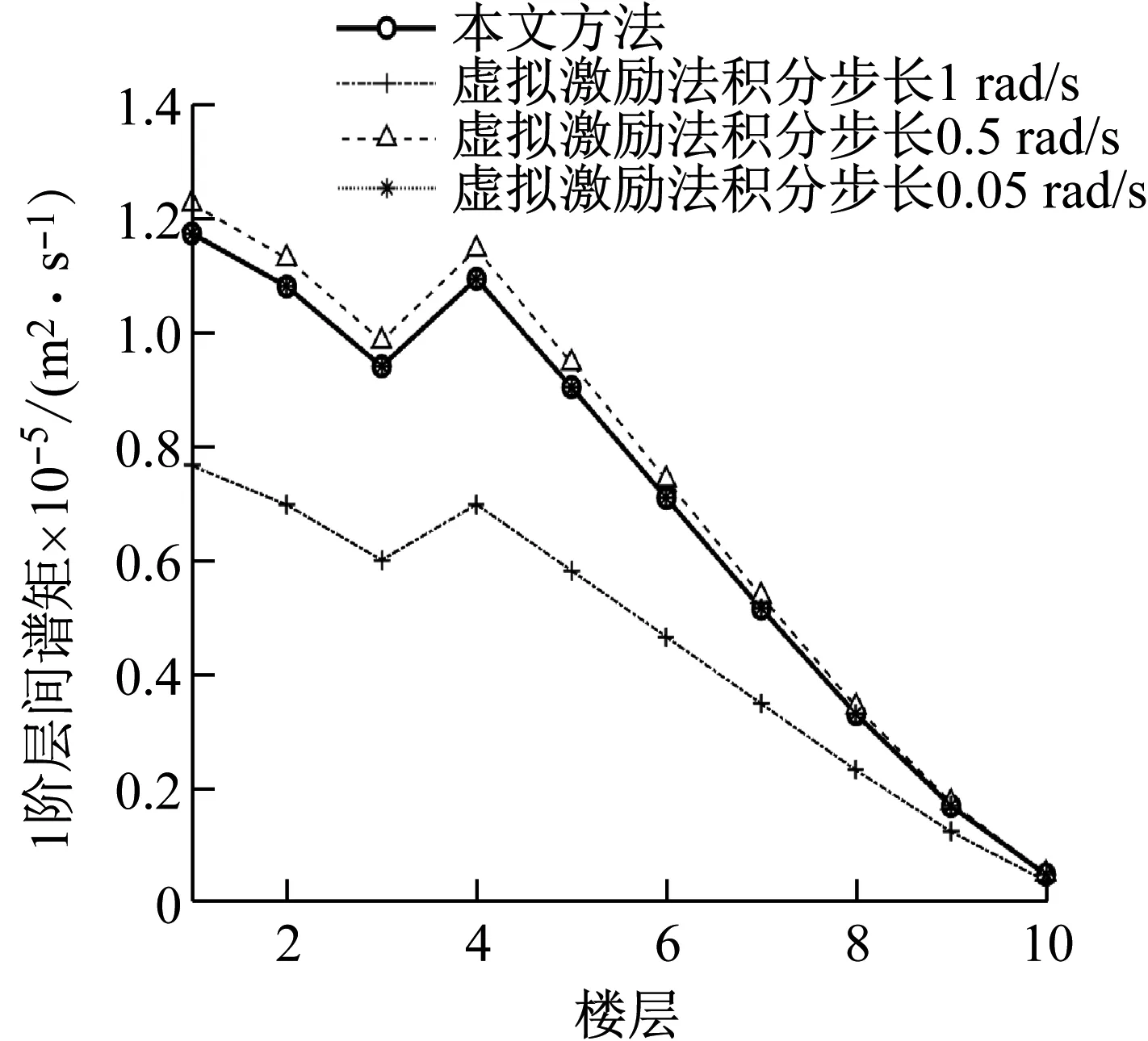
图7 层间位移1阶谱矩对比图Fig.7 Comparison diagram of 1st order spectralmoments of interlayer displacement

图8 层间位移2阶谱矩对比图Fig.8 Comparison diagram of 2nd order spectralmoments of interlayer displacement

4.2 虚拟激励法积分区间的确定

由“4.1节”可知，本文方法所获得谱矩为精确解，且可用来验证虚拟激励法的精度。而目前文献对于虚拟激励法的积分区间没有明确的规定，为此，本文对其合理的积分区间进行了研究。“4.1节”研究表明积分步长取0.05时虚拟激励法基本与本文方法重合，为此，分别取积分区间上限为5 rad/s，25 rad/s，100 rad/s，按积分步长为0.05 rad/s进行分析。从图9～12可知，积分上限取25 rad/s,结构响应0-2阶谱矩和加速度方差均可以达到较好的精度。

图9 虚拟激励法中积分区间对位移0阶谱矩影响Fig.9 Influence of integral interval on 0 order spectralmoment of displacement by PEM

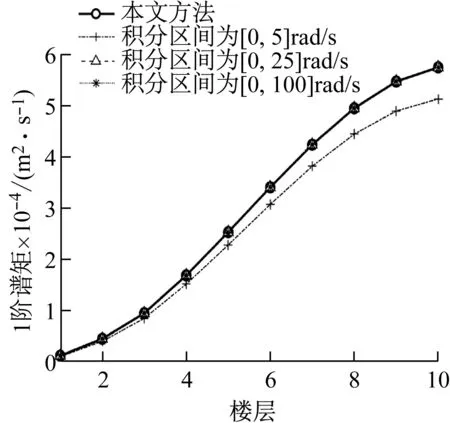
图10 虚拟激励法中积分区间对位移1阶谱矩影响Fig.10 Influence of integral interval on 1 st order spectralmoment of displacement by PEM

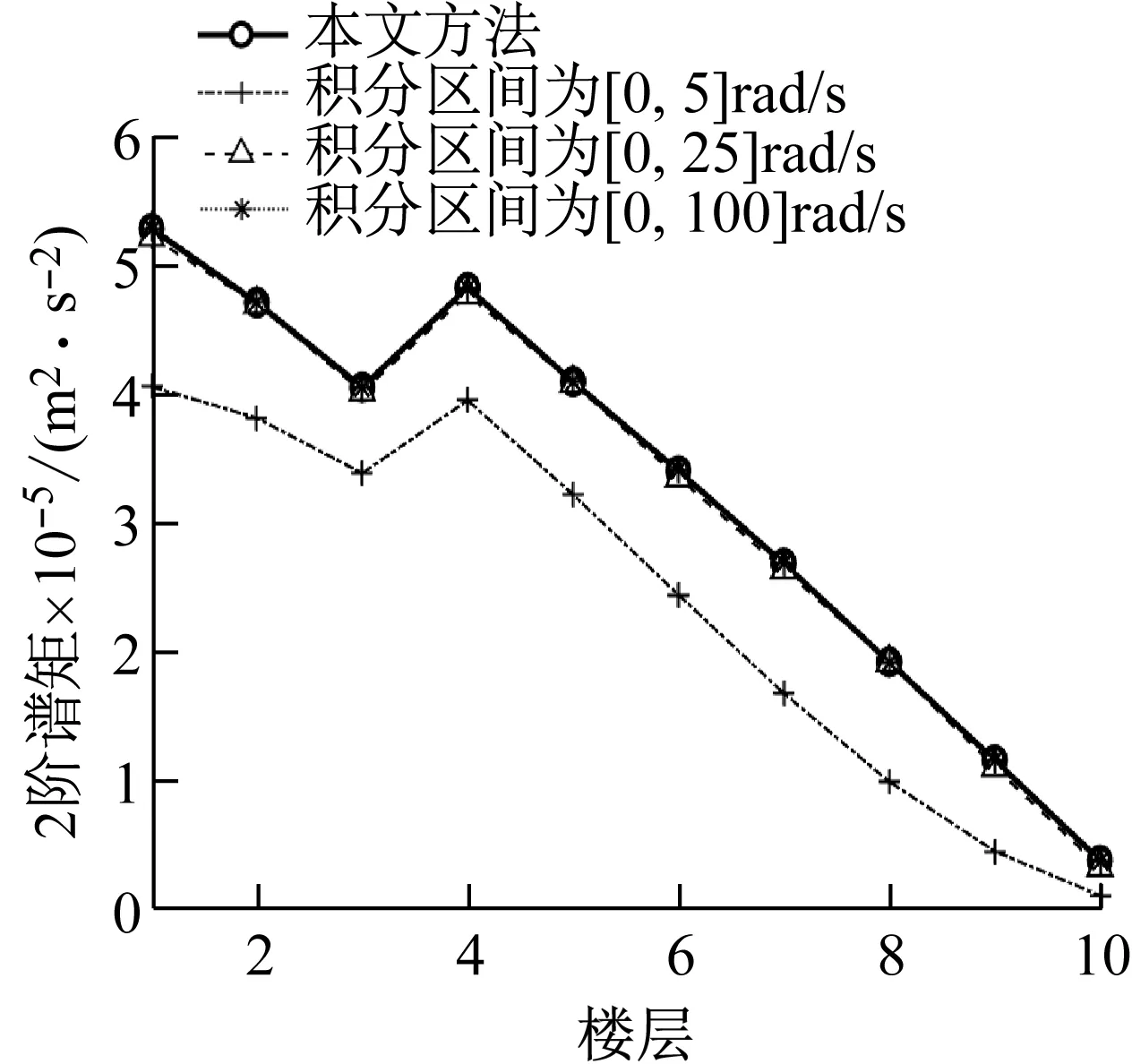
图11 虚拟激励法中积分区间对层间位移2阶谱矩影响Fig.11 Influence of integral interval on 2nd order spectralmoment of interlayer displacement by PEM

5 结 论

本文提出了结构频响函数的二次正交法，并成功获得了结构基于Davenport风速谱激励下系列响应的0-2阶谱矩及4阶谱矩的简明封闭解，获得如下结论：

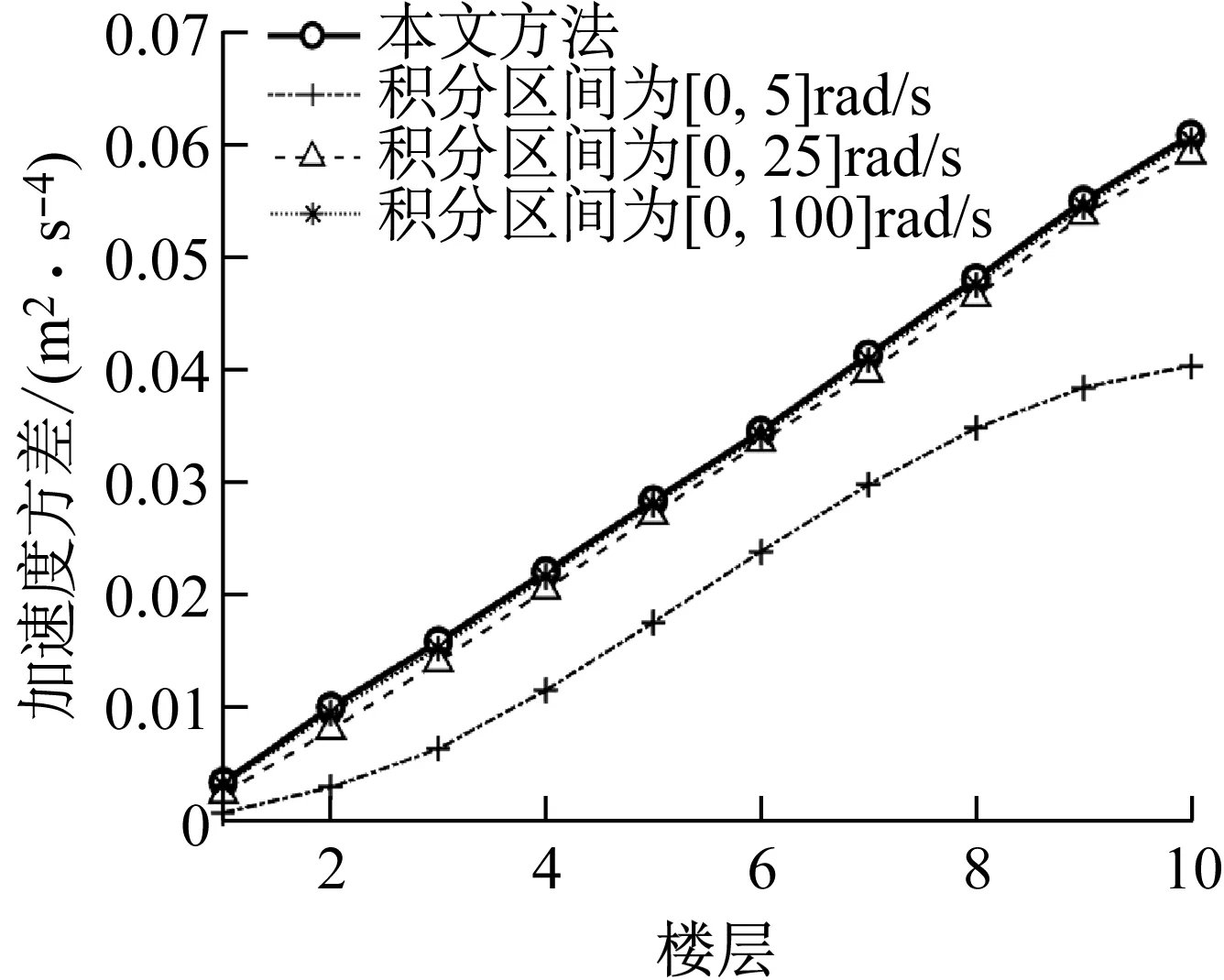
图12 虚拟激励法中积分区间对结构加速度方差影响Fig.12 Influence of integral interval on structuralacceleration variance by PEM

(1) 应用复模态法将结构振动体系解耦为一阶微分方程组，利用一阶微分方程的虚拟激励法获得了结构系列风振响应(结构层绝对位移和层间位移)的功率谱密度函数，该函数是关于系统振动复特征值与频域变量的平方和的线性组合，称之为频响函数的二次正交化。

(2) 由于获得了结构系列响应功率谱的二次正交式，从而利用谱矩的定义成功获得了结构风振响应的0-2阶及4阶的谱矩的简明封闭解。而响应的0阶谱矩等于响应的方差，2阶谱矩等于响应变化率的方差，从而获得了结构系列响应的方差，为基于首超破坏的动力可靠度分析奠定了基础。

(3) 通过与传统虚拟激励法进行对比，说明本文方法分析结构系列响应的谱矩和方差为封闭解，不受积分区间和积分步长的影响；同时可以用来验证传统虚拟激励法的精度。

附录A 频响函数SDl(ω)的推导

对文中式(22)进行整理：

(A.1)

式中：

(A.2)

(A.3)

(A.4)

把式(19)代入式(A.3)：

利用式(9)，则式(A.5)简化为：

(A.6)

(A.7)

把式(19)代入式(A.4)：

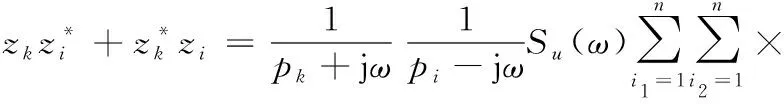
ηi,i1ηk,i2I0(Hi1)I0(Hi2)B(Hi1)B(Hi2)+

I0(Hi1)I0(Hi2)B(Hi1)B(Hi2)

(A.8)

由式(9)，则式(A.8)改写为：

(A.9)

(A.10)

针对式(A.9)中的以下部分进行简化：

把式(A.11)代入式(A.9)则：

(A.12)

把式(A.6)、(A.12)代入式(A.1)，则结构脉动风压力的动力响应的功率谱：

(A.13)

附录BΧk,q(q=0,2)的推导

B.1Χk,0的推导

(B.1)

令：

t=(1+a2ω2)1/3

(B.2)

由式(B.2)得：

(B.3)

把(B.2)、(B.3)代入式(B.1)：

(B.4)

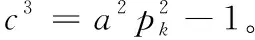
对式(B.4)中部分进行因式分解：

(B.5)

对式(B.5)进一步简化：

(B.6)

把式(B.6)代入式(B.4)并积分：

(B.7)

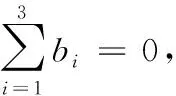
(B.8)

B.2Χk,2的推导

令：t=(1+a2ω2)1/3，则

(B.10)

(B.11)

把式(B.11)代入式(B.9):

(B.12)