基于隔振器荷载特征的非线性隔振器设计方法研究

杜香刚

(1.中国铁道科学研究院集团有限公司铁道建筑研究所， 北京 100081；2.高速铁路轨道技术国家重点实验室，北京 100081)

传统的隔振器往往由于自身的固有频率无法降到足够低而难以实现期望的隔振目标，主要体现在低频隔振性能差，以及缺乏可调控性和自适应能力等方面[1-2]。高承载能力和低固有频率之间的矛盾成为被动隔振技术发展的瓶颈，低频隔振尤其是重型设备的低频隔振也一直是被动隔振的难点问题[3-4]。

随着我国城市化进程加快，地铁引起的环境振动问题越来越受到人们的重视，因此，在地铁轨道设计时采用了多型减振措施。在众多轨道减振措施中，钢弹簧浮置板轨道被认为是减振效果最好的减振轨道形式。经大量测试，钢弹簧浮置板轨道能够有效抑制高频振动，但对低频振动抑制效果并不明显，特别是对于实验室、博物馆等建筑物内精密仪器和珍贵文物十分敏感的10 Hz左右振动成分难以达到理想的衰减效果。

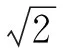
随着振动控制要求的不断提高，基于非线性理论的隔振技术的研究和应用越发广泛[9-11]，非线性系统可以通过自身阻尼非线性和刚度非线性来改善系统本身的隔振性能[12-14]。非线性隔振技术可以根据系统激励及振动特点进行最优参数设计，因此，利用非线性被动隔振技术解决既有线性隔振系统存在的问题是城市轨道交通减振轨道设计的重要方向。一种名为SD振子的非线性系统于2006年被曹庆杰教授所提出，这类系统由一个被一对斜拉弹簧所约束的质量块构成。研究表明，SD振子是一种典型的几何非线性特征的非线性系统，大量学者对SD振子的丰富的动力学行为进行了详细的研究，同时由于其几何参数的可调性，可以广泛应用于低频、超低频隔振等工程领域，朱光楠等对SD振子系统在变压器抗震领域的应用进行了系统、详细的理论以及试验研究。

本文基于非线性隔振理论，在隔振器荷载特征分析的基础上，提出了基于隔振器荷载特征的非线性隔振器设计方法，对隔振器的刚度和阻尼曲线进行非线性设计优化，使得隔振器同时具有良好的低频隔振性能和振动位移控制能力。

1 基于隔振器荷载特征的非线性隔振器设计流程

传统浮置板轨道的设计方法是以线性隔振理论为基础的设计方法，即根据环评要求和地铁设计相关规范，设计具有满足规范要求和施工要求的浮置板轨道的固有频率及隔振器刚度，以经验为基础确定浮置板轨道的基本结构尺寸及隔振器的初步布置方式；在此基础上根据车辆轴重、轴距等信息对浮置板的结构及隔振器的刚度及布置方式进行校核。传统设计方法往往只针对系统的减振性能进行设计而无法兼顾轮轨系统的动力学行为，更无法考虑轮轨动态激励引起的隔振器荷载特征，因此导致了浮置板轨道在实际使用中存在对低频隔振性能差和轮轨系统振动响应大等问题。

鉴于以上原因，本文提出了基于隔振器荷载特征的非线性浮置板减振轨道系统的设计方法(如图1所示)，首先建立车辆-轨道-隧道系统动力学模型(模型经过实测数据修正)进行系统动力学分析计算，在对隔振器荷载特征识别的基础上，运用非线性动力学优化模型进行浮置板非线性隔振器的刚度及阻尼曲线优化设计，最后将优化得到的非线性特征曲线带入车辆-轨道-隧道动力学模型进行分析验证。

图1 基于隔振器荷载特征的非线性隔振器设计流程

2 车辆-轨道-隧道耦合动力学模型

建立车辆-轨道-隧道耦合动力学模型获取隔振器荷载，并对设计的非线性特征曲线进行分析验证是本文设计方法的基础。因此，该模型需包含列车模型、浮置板轨道模型、隧道模型及轮轨接触模型，可以将钢弹簧设计为非线性曲线来模拟非线性隔振器。以某地铁线路的浮置板轨道为例(如图2所示)，根据某B型地铁车辆及轨道和隧道的动力学参数(如表1所示)建立如图3所示的车辆-浮置板轨道-隧道系统一体化仿真分析模型，其中车辆系统主要由车体、转向架、轮对和一系、二系悬挂组成。对车辆模拟时，将车辆的基本部件近似处理为刚体，各基本部件之间通过弹性或刚性约束来限制车辆结构中各部件间的相对运动。模型中浮置板轨道系统由钢轨、扣件、轨道板及钢弹簧组成，其中轨道板采用实体单元建模，钢轨采用铁木辛柯梁模拟，扣件采用弹簧阻尼单元进行模拟，钢弹簧采用非线性弹簧力元。轨道设置为：普通整体道床+5段25 m长浮置板道床+普通整体道床，建立浮置板轨道时既考虑了板与板之间起连接作用的剪力铰，又考虑浮置板间钢弹簧的局部加密情况(如图4所示)。为了能够反映相邻车辆转向架对浮置板以及钢轨动态下沉量和扣件力的影响，本文采用三车模型进行仿真模拟。轮轨接触采用UM柔性轨道模块中自带的Kik-Piotrowski多点非赫兹接触模型来计算轮轨蠕滑力，该模型可以考虑车轮和钢轨的微小穿透，法向压力分布沿前进方向呈椭圆形状，切向接触斑形状为非椭圆。模型中地基和隧道结构采用实体单元模拟，由于有限元模型只能在有限范围内求解振动的传播问題，由于主体的实际情况是无边界的形式，因此在模型截取的界面上会发生波的反射，导致模型结果失真，因此本模型采用低反射边界，在模型边界的节点上的法向和切向设置弹簧阻尼元件来模拟无限范围对计算范围的效果。模型的仿真结果经过与实测数据进行对比修正后[15]，取列车的运行速度为80 m/h的隔振器支反力作非线性系统的设计输入。

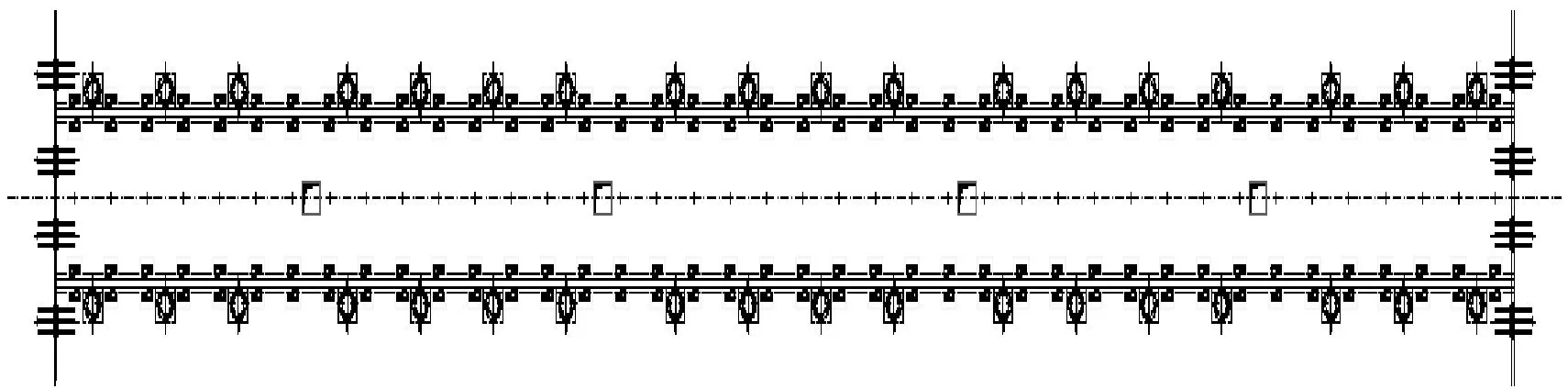
(a) 纵向布置图

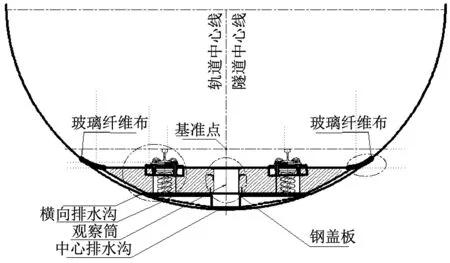
(b) 断面结构图图2 浮置板轨道结构图Fig.2 Structure graphing of floating slab system

表1 建模基本参数Tab.1 Basic parameters of modeling

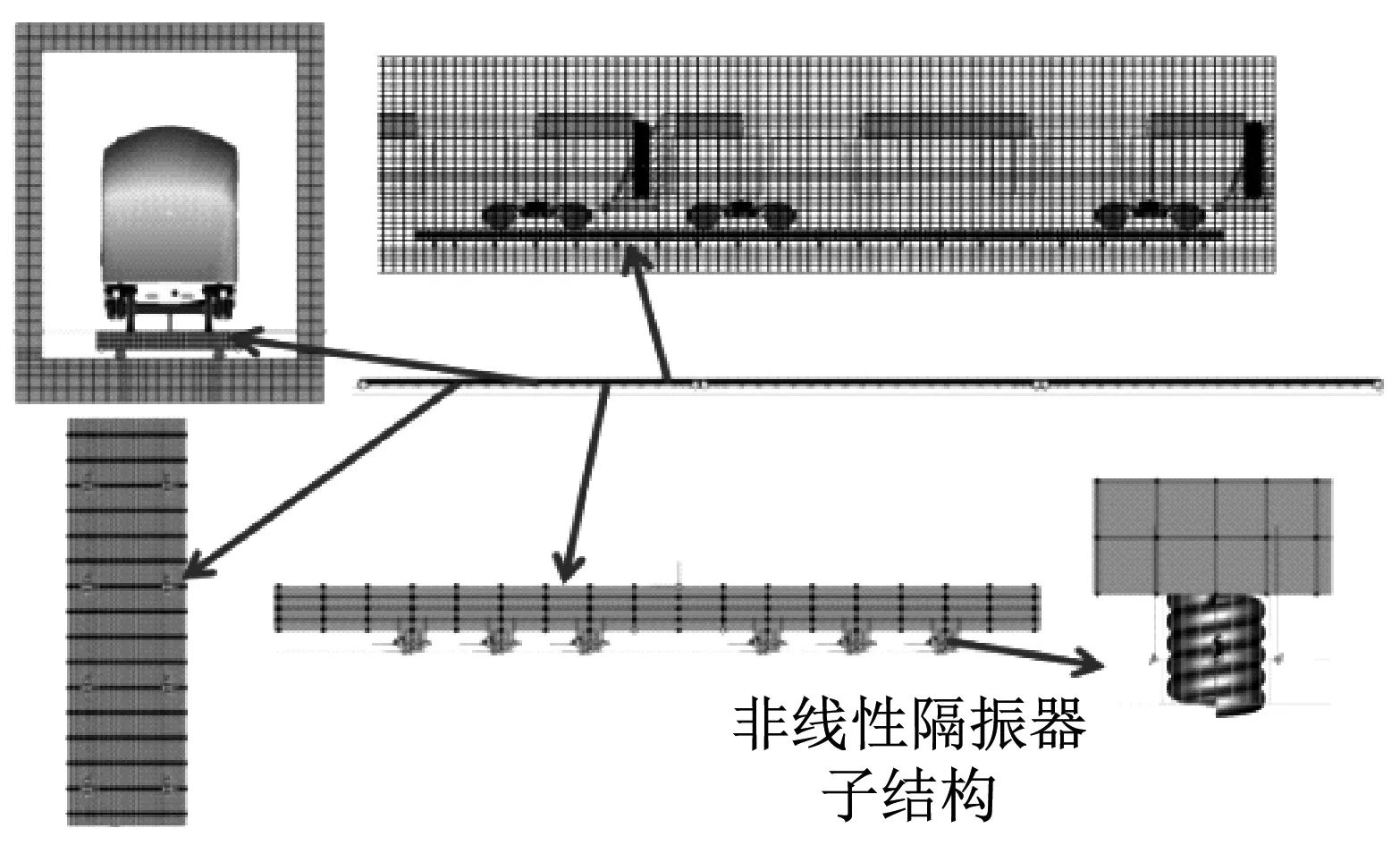
(a) 一体化仿真模型

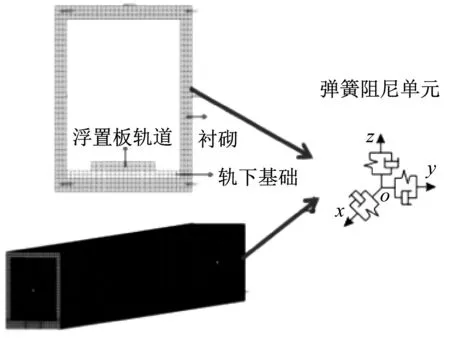
(b) 隧道模型图3 车辆-轨道-隧道一体化仿真模型Fig.3 The system dynamic model

(b) 正视图图4 车辆-浮置板轨道耦合动力学仿真分析模型Fig.4 Vehicle-floating slab track system couplingdynamic simulation model

3 浮置板轨道用隔振器荷载特征识别

根据第2章建立的模型，提取中间板端部、中部和尾部隔振器的垂向荷载时间历程(如图5所示)，由图可知浮置板中部隔振器受力最大，端部和尾部隔振器受力相对较小，这是由于浮置板中部板的柔性较大，端部和尾部隔振器间距较小的原因。因此在后续分析中，以受力最大的中部隔振器作为研究对象。对板中部隔振器荷载曲线进行频谱分析，如图6所示，可以看到隔振器荷载分为准静态冲击荷载部分(4 Hz以下，移动质量引起的冲击荷载，以下简称冲击荷载)与动态荷载(4 Hz以上，以下简称动态荷载)，且冲击荷载要远大于动态荷载，冲击荷载主要影响浮置板位移，而动态荷载主要影响环境振动。

图5 隔振器垂向荷载Fig.5 Vertical loads of floating slab isolators

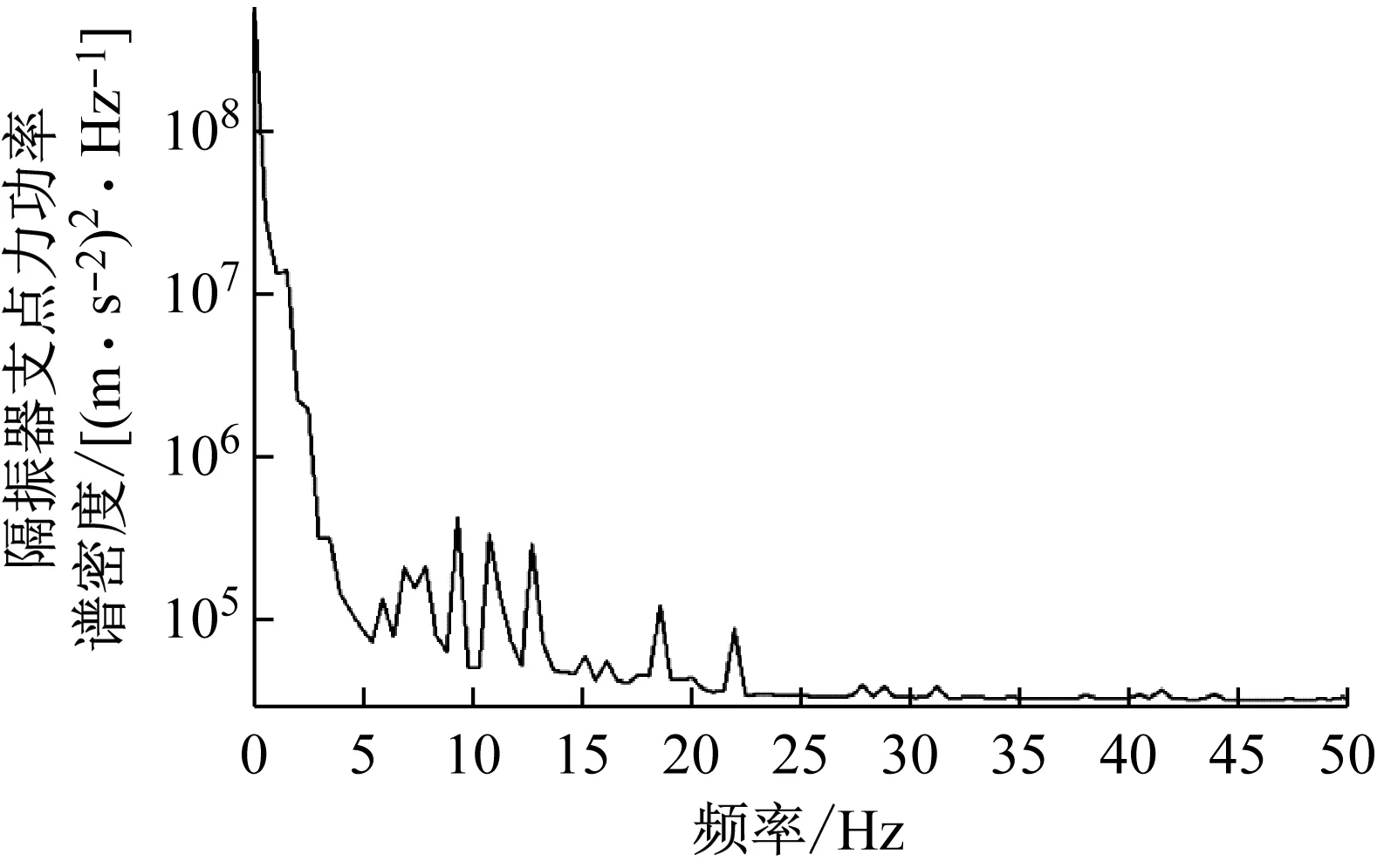
图6 板中隔振器荷载功率谱密度图Fig.6 PSD diagram of isolator loads in themiddle of floating slab

准确地提出非线性浮置板轨道系统的控制及优化目标是非线性浮置板轨道隔振器参数设计的关键，因此需要结合列车经过浮置板轨道的动态过程对隔振器荷载的特征进行分析。图7为列车经过浮置板轨道的全过程，从图中可以看出，在静平衡位置处(分别对应列车开始驶入和刚驶出浮置板)的隔振器荷载的振荡为隔振器未受到列车冲击荷载时的自由振动；当列车进入浮置板轨道时，在冲击荷载上叠加有动态的随机振动荷载。非线性隔振器的设计需要同时考虑浮置板的位移控制与振动控制，因此，需将隔振器荷载按照冲击荷载与动态荷载进行分解，如图7所示。从图中看到，隔振器冲击荷载呈现4个峰(谷)值，P1为两节车相邻转向架引起的荷载最小值；P2为头尾转向架引起的荷载最小值；P3为头尾转向架作用于隔振器上的最大荷载，P4为两节车相邻转向架作用于隔振器上的最大荷载，如表2所示。表2中AW0为空载工况，AW2为正常荷载工况，AW3为满载工况。从图7(b)可以看出，动态荷载的振动能量主要集中在10 Hz附近。

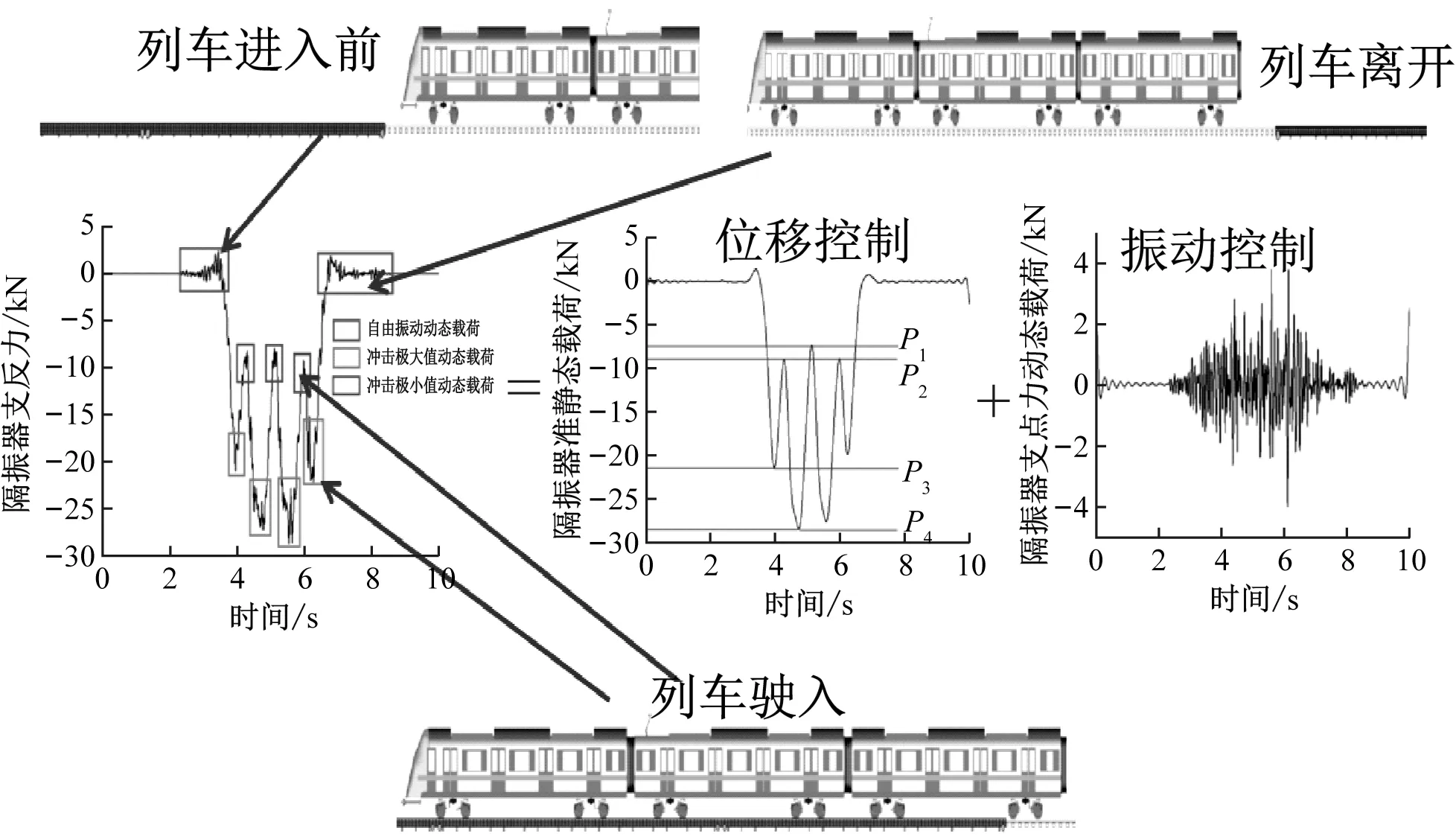
(a)

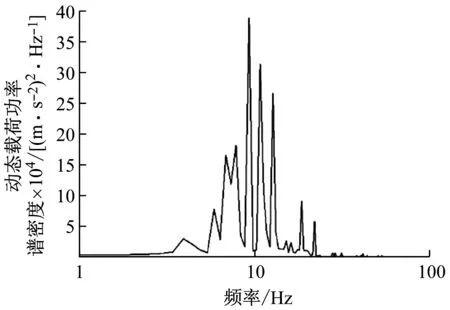
(b)图7 隔振器荷载特征分析图Fig.7 Floating slab isolator loads characteristics analysis

表2 不同工况下隔振器冲击荷载极值Tab.2 Extreme value of isolator shock loads under different working conditions kN

因此，基于以上隔振器荷载动态特征，定性判断所构造的非线性刚度曲线应保证系统在静平衡位置处(即车辆驶来浮置板前及车辆驶离浮置板后)和冲击荷载的极值位置处具有较好的隔振效果，同时抑制车辆驶来和离开后浮置板的自由振荡以及冲击动荷载引起的振荡。为保证系统具有足够的储能能力，令系统的大刚度区间尽可能发生在无明显振荡区域，且令系统最大刚度值在保证储能能力的前提下尽可能小。

4 非线性隔振器刚度曲线优化设计

4.1 非线性动力学优化模型

本文基于SD振子几何非线性隔振理论，根据实际设计需求和目标构造非线性动力学方程，进而获得满足实际情况的最优设计参数，并依据设计参数选择满足设计参数要求的最优结构形式。建立的单隔振器力学模型如图8所示，图中振子m在竖直方向振动，其通过承载弹簧和阻尼与基础相连，垂直弹簧为系统提供正向承载力。水平弹簧-连杆机构为系统提供负刚度，连杆一端与质量为m的振子铰接，另一端铰接于水平放置的弹簧，弹簧末端与基础相连。水平弹簧的刚度为k1，竖向弹簧刚度为k0，阻尼为C，非线性系统的初始平衡位移距离水平弹簧的高度为d，连杆长度为l，弹簧原长为L，水平弹簧原长末端到振子中心的水平距离为B。正常工作状态下，竖向弹簧k0处于预压缩状态来承载浮置板和列车的重力荷载，水平弹簧k1处于预压缩状态保证弹簧-连杆机构为系统提供负刚度，使得正负刚度并联在振动范围内形成非线性刚度，从而达到低频隔振的目的。

肝龙胶囊对猪血清诱导的肝纤维化大鼠的治疗作用……李 燕，邵明园，国 超，杨强丽，曹昌娥，赖 泳（13）

图8 浮置板-非线性隔振器示意图Fig.8 Vibration isolator physical model

图8所示的非线性动力学方程为式(1)，基于该动力学方程，根据优化目标进行非线性刚度曲线的设计。

(1)

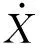
4.2 隔振器非线性刚度曲线设计方法

图9所示为非线性隔振器刚度曲线设计原理示意图，图中虚线表示传统钢弹簧隔振器刚度曲线示意图，红线表示非线性隔振器刚度曲线示意图。根据实际工程设计需求，分别按照起始隔振频率控制需求、振动位移控制需求和振动衰减速度控制需求三方面对非线性隔振曲线进行设计。

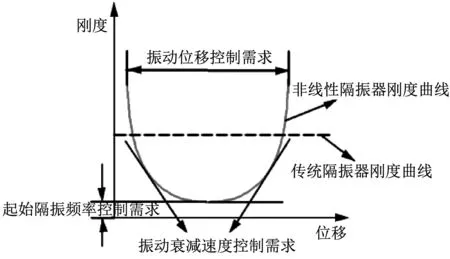
图9 非线性隔振器刚度曲线设计原理图Fig.9 Schematic diagram of nonlinear isolator stiffness curve

根据第1章的分析，隔振器的支反力响应可以被分解为冲击响应和随机响应两部分。其中冲击响应部分可视为由车辆驶入导致隔振系统荷载质量变化引起的具有振幅大、频率低的响应；而随机响应部分则可以视为由轮轨接触引发的具有振幅小、频率高的响应。

为保证车辆行驶的平稳性，以及对隔振系统的隔振性能的要求，需同时保证车辆加载至浮置板上后浮置板的振动位移不可过大，以及隔振器向地基所传递的能量相比线性系统有所衰减。利用4.1节介绍的力学模型，设置非线性刚度曲线的优化指标：浮置板振动位移峰峰值不超过3 mm；浮置板隔振系统通过隔振器传递至地基的振动能量，在低频段(≤20 Hz)相比线性系统存在明显衰减效果；在隔振器荷载强度大的位置处系统相比线性系统存在明显的衰减效果。

考虑到车辆自重不变，可以视为车辆驶入时向隔振系统输入一固定的准静态力，进而应使隔振系统在受到车辆准静态作用后，进入隔振区段。因此对于隔振器进入隔振区间的位置可根据P0、P1、P2、P3以及P4点的发生位置进行确定，上述各个荷载值所对应的位移分别被称为X0、X1、X2、X3以及X4，从而提升系统对随机振动部分的抑制能力。简言之，基于系统冲击响应部分特征决定荷载位移的控制能力，而基于对随机响应部分特征决定隔振器的隔振能力。

因此通过结合荷载分析结果，考虑设计一种非线性隔振器，旨在保证在系统具有对浮置板足够的承载能力；以及在空载至准静态荷载之间具有足够的等效刚度抑制响应位移；同时保证系统在随机荷载集中的位置附近具有较高的隔振性能。因此，根据隔振器荷载特征，基于如图8所示的模型所具有的结构参数，通过大量仿真计算优化设计见图10线性隔振器恢复力-位移曲线和图11非线性隔振器恢复力-位移曲线。

图10 线性隔振器恢复力-位移曲线图Fig.10 Linear force-displacement curve

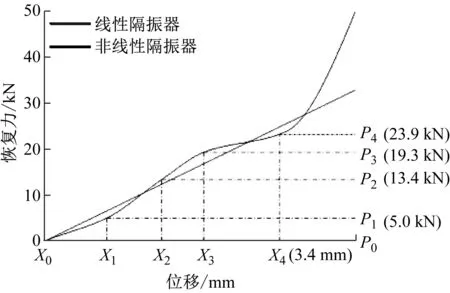
图11 非线性隔振器恢复力-位移曲线图Fig.11 Nonlinear force-displacement curve

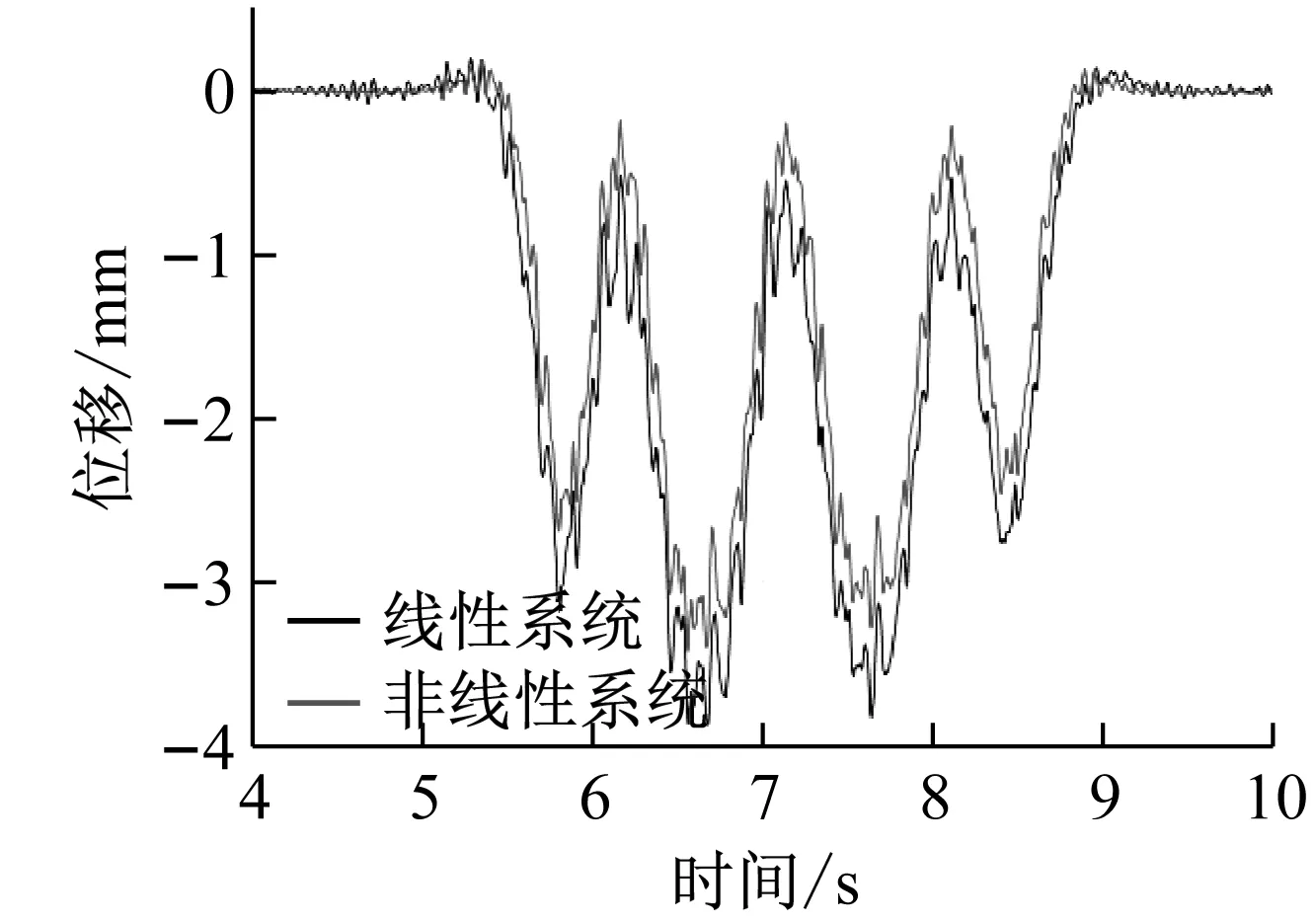
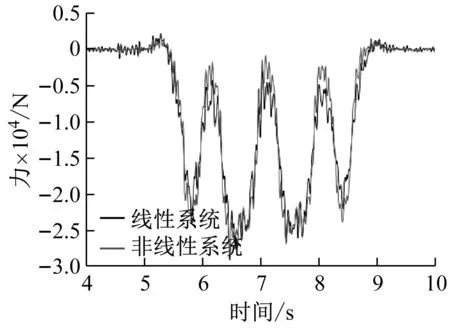
将非线性隔振器恢复力曲线代入图3所示的车辆-轨道-隧道耦合动力学模型，得到图12(a)浮置板振动位移响应曲线图，从图中可以看出，非线性隔振系统相比原有线性系统的浮置板动态位移具有明显的抑制效果，最大动态位移减小约20%左右；图12(b)为非线性隔振系统在车辆运行时引起的隔振器支反力响应曲线。从图中可以看出，相比原有线性系统在荷载位置P0以及在和位置P3、P4处响应具有明显的抑制效果；图12(c)为隔振器支反力响应的功率谱密度曲线的对比图，从图中看出，非线性隔振系统同时在低频和高频上产生了明显的振动隔离能力，进而相比线性系统在几乎全频段上均体现出振动的衰减效果。

5 非线性隔振器阻尼曲线优化设计

在工程中常会有一些不规则的冲击和振动，因而适当增大钢弹簧隔振器阻尼可以抑制系统在这种冲击和振动作用下的振幅，并使自由振动很快消失，尤其当系统发生共振时，可以极大程度的抑制共振频率处的响应。但对于传统线性黏性阻尼来说，增大阻尼虽然可以减小共振频率下的响应，但会降低隔振区的隔振效率。因此，本章基于隔振器荷载特征，设计隔振器非线性阻尼曲线，使得阻尼在减小共振峰值的同时不放大高频荷载的振动传递。

(a) 浮置板位移动态响应曲线图

(b) 隔振器支反力动态响应曲线图

(c) 隔振器支反力响应功率谱密度曲线对比图图12 非线性隔振系统效果对比图Fig.12 Response diagrams of nonlinear isolator andtraditional isolator system

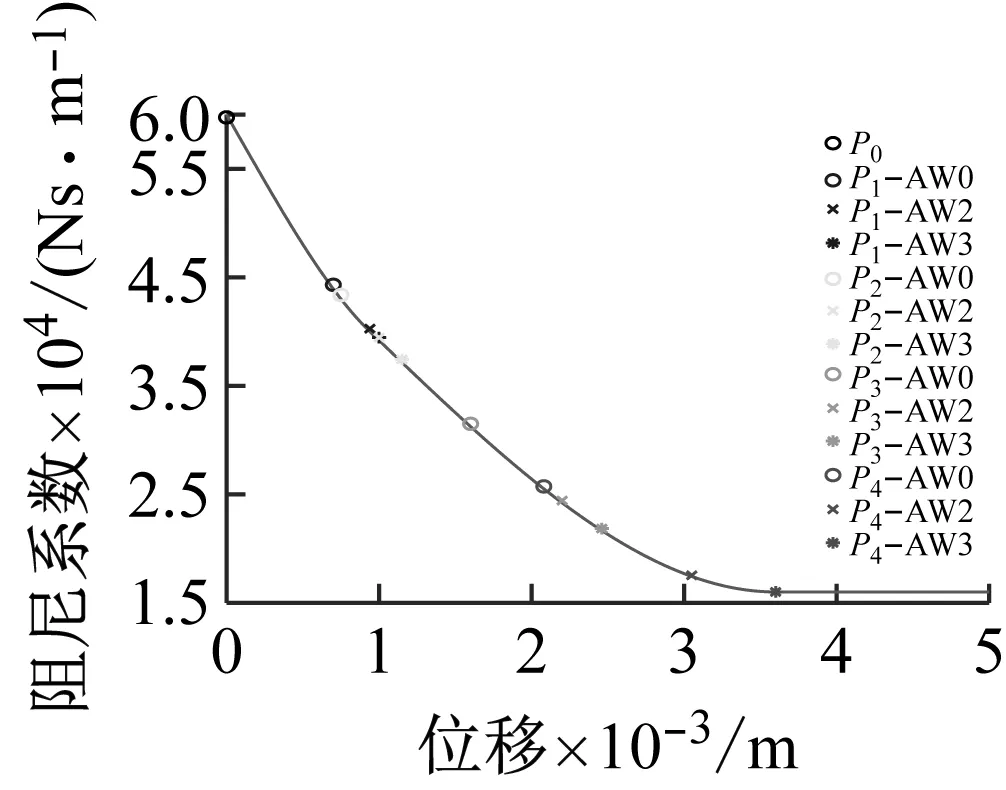
由2.2节分析结果可知，优化出的非线性刚度隔振器在P1、P2位置处存在振动放大现象。因此在本节在最优刚度曲线的基础上，设计隔振器最优阻尼曲线，进一步提高非线性隔振器性能。在第3节荷载分析的基础上，分别设计4种非线性阻尼曲线(阻尼系数随位移非线性变化)，分别是渐小非线性阻尼曲线、渐大分线性阻尼曲线、先大后小非线性阻尼曲线和先小后大非线性阻尼曲线(如图13所示)，通过系统动力学仿真方法，确定最优阻尼曲线。

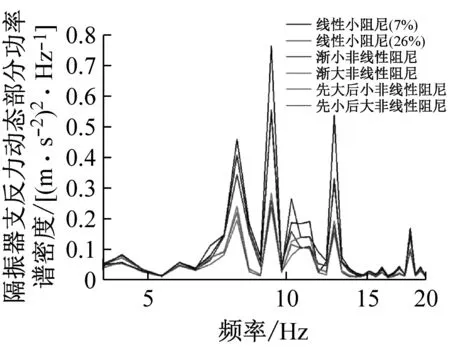
分别将4种非线性阻尼曲线代入图3所示的车辆-轨道-隧道耦合动力学分析模型中进行优化计算，优化目标为隔振器支反力，其结果如图14所示。从图14(a)、(b)隔振器支反力时域曲线可以看出，在动态荷载较大的位置P1、P2处施加大阻尼可以极大程度抑制动态荷载峰值。从14(c)、(d)、(e)可以看出，线性大阻尼、先大后小非线性阻尼和渐大阻尼在低频(≤20 Hz)及中高频(>20 Hz)有较好的振动抑制效果。

(a) 渐小阻尼

(a) 隔振器支反力

(d) 支反力低频部分功率谱密度放大图

6 非线性减振轨道系统仿真验证

将优化后得到的非线性刚度和非线性阻尼曲线带入图3所示的车辆-轨道-隧道系统动力学模型中，模拟列车运行工况下非线性轨道系统的隔振效果和轨道动态响应，仿真得到浮置板振动加速度及隧道壁分频振级图见图15(a)、(b)所示。从图15(a)中可以看出，非线性隔振器可以显著降低浮置板轨道的振动加速度响应，振动加速度有效值从1.04 m/s2降低到了0.39 m/s2，降低约62%。从图(b)中可以看出，相比既有线性系统，非线性系统在全频段都具有较好的衰减效果，Z振级插入损失约为3 dB；在低频段(≤20 Hz)，非线性系统的隔振效果远优于线性系统，分频最大振级插入损失约为12 dB。

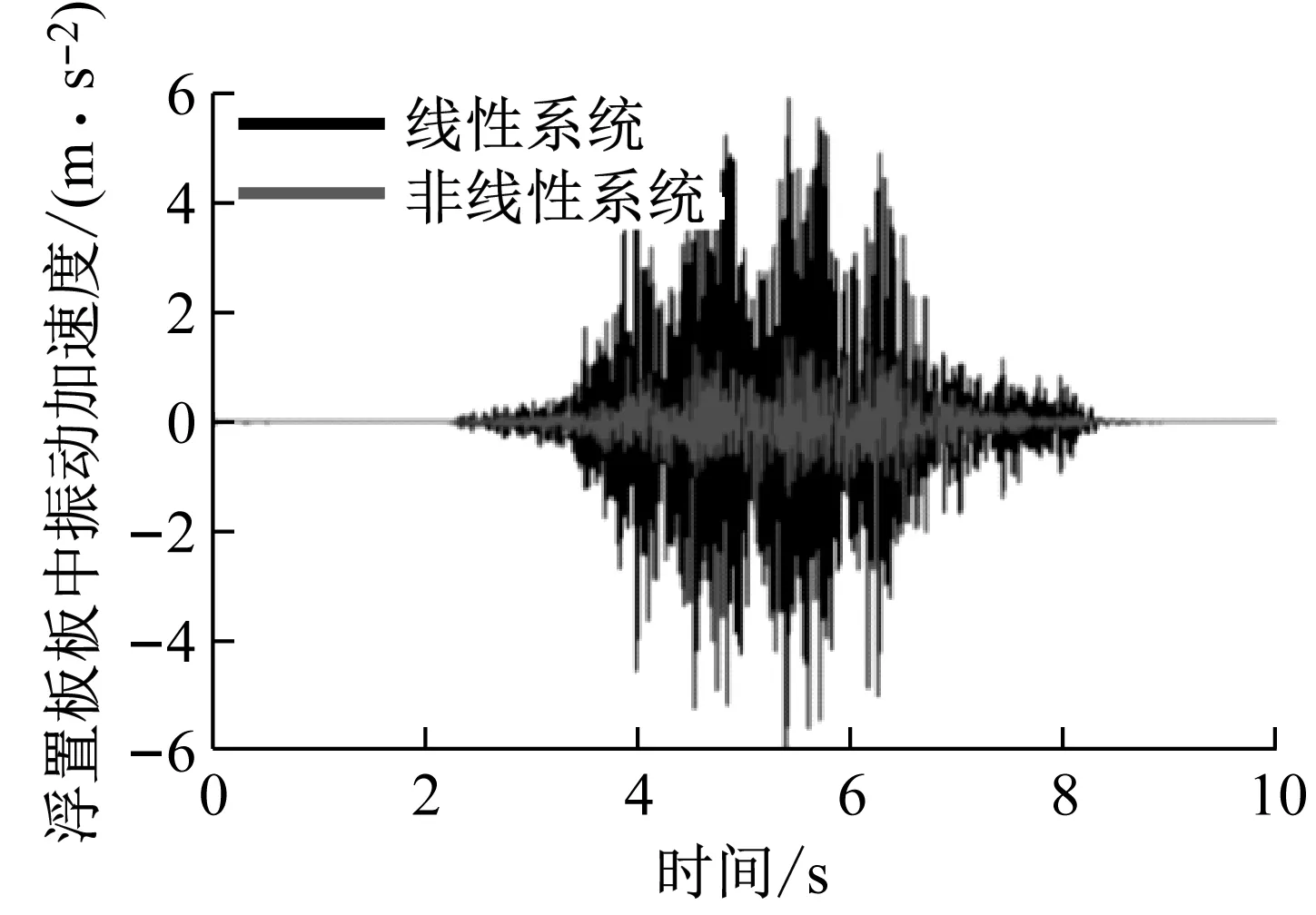
(a) 浮置板加速度

7 结 论

本文基于非线性隔振理论，在隔振器荷载特征分析的基础上，对浮置板减振轨道用隔振器的刚度和阻尼曲线进行非线性设计优化，使得非线性浮置板减振轨道同时具有良好的低频隔振性能和动态位移控制能力。利用车辆-轨道-隧道耦合动力学评估模型进行仿真研究，得出以下结论：

(1) 相比既有线性系统，采用非线性隔振器的非线性浮置板减振轨道系统可有效控制轨道板动态位移，轨道板动态位移可降低约20%。

(2) 相比既有线性系统，非线性浮置板减振轨道系统可显著降低轨道板的振动加速度响应，振动加速度有效值可降低约62%。

(3) 相比既有线性系统，非线性浮置板减振轨道系统在全频段都具有较好的衰减效果，Z振级插入损失约3 dB，在低频段(≤20 Hz)非线性系统的隔振效果优于线性系统，分频最大振级插入损失约12 dB。

上述理论研究结论在实际应用中能否达到理想效果，应在非线性隔振器结构设计、制造公差控制和非线性减振轨道系统整体施工上开展系统研究。