圆台形滑阀反馈节流静压支承性能分析

曾永龙, 彭文杰，2, 杜 涛, 陈 军

(1.宝钢股份研究院 武钢有限技术中心， 湖北 武汉 430080； 2.武昌理工学院 人工智能学院， 湖北 武汉 430223)

引言

液体静压支承技术广泛应用于轧机轧辊轴承、伺服液压缸、精密机床主轴等场所，其中恒压供油静压支承方式主要是通过固定式或反馈式节流器调节控制承受负载的主轴，使主轴以很小的位移变化来适应不同外载荷的作用[1-8]。相比固定式节流器，反馈式节流器的调节能力更好，多用于负载变化较大的系统，其常用结构形式主要包括滑阀型和薄膜型两种。滑阀型的阀芯一般呈圆柱体结构，加工制造简单，但其间隙流量与阀芯位移量的一次方成比例，支承腔的排量与支承间隙的三次方成比例，支承间隙的微小变化需要阀芯较大的位移量响应反馈，动态性能较差。薄膜型的薄膜与圆台的间隙的流量与薄膜形变间隙的三次方成比例，动态性能较好，但其加工制造难度大，且膜片易产生永久塑性翘曲变形[9-12]。针对这一问题，设计了阀芯是圆台形结构的滑阀反馈节流器。圆台形滑阀反馈节流器的阀芯结构方便加工制作，且不会因压差作用产生塑性形变，长期使用时动态响应性能与薄膜型节流器相当，并对其静压支承性能进行了分析。

1 圆台形滑阀节流器构造及原理

圆台形滑阀节流器结构及其静压支承原理如图1所示，高压油以恒定的压力ps由进油口注入滑阀阀体内，滑阀节流器阀芯的两端是有一定锥度的圆台形结构，其在滑阀腔体内往复运动时，与阀体之间的间隙节流减压作用后，以一定的压力进入上、下支承腔内。支承油腔上、下对向布置，承载件在两油腔的压力差作用下处于平衡位置。上、下支承腔的油液通过油腔封油边流回油箱。

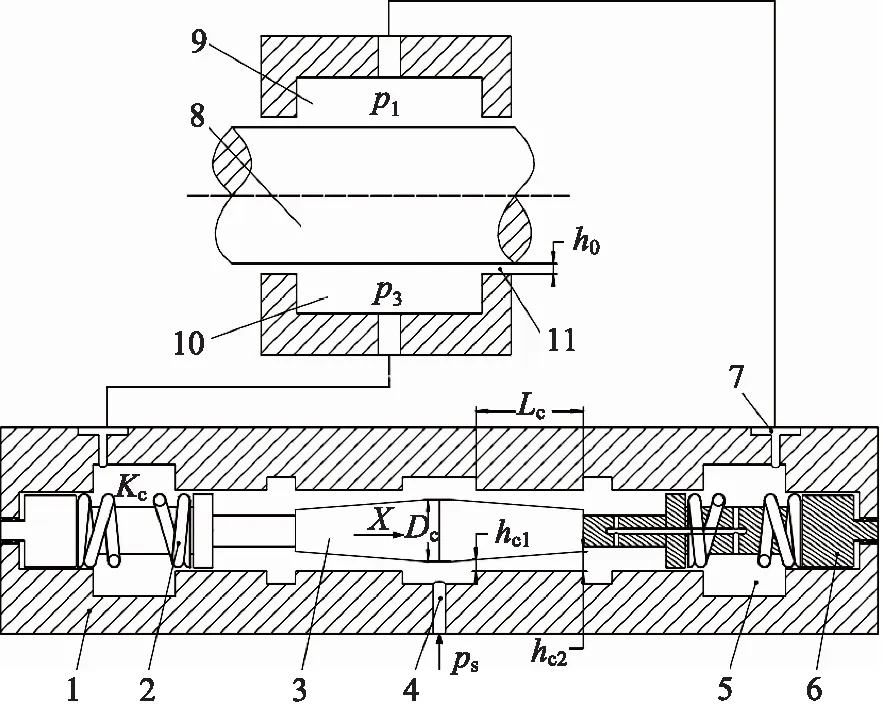
1.滑阀阀体 2.滑阀弹簧 3.阀芯 4.滑阀进油口 5.弹簧腔 6.弹簧调节螺钉 7.滑阀出油口 8.承载件 9.上支承腔 10.下支承腔 11.封边间隙

2 静态性能分析

2.1 静态流量平衡方程

阀芯位于空载平衡位置时，上下支承腔内压力相等，均为pb0，且各支承腔经封油边间隙的回油流量相等。

经圆台形阀芯两端节流间隙进入支承腔的流量QIn为：

(1)

经上、下支承腔流出的流量QOut均为：

(2)

外加载荷作用时，阀芯发生位移，经滑阀两端流入上、下支承腔的流量QIn1，QIn3分别为：

(3)

(4)

经上、下支承腔封油边间隙流出的流量QOut1，QOut3理论值为：

(5)

(6)

式(5)、式(6)中，h1，h3分别是上下支承油腔内的封油边油膜厚度。联立式(3)～式(6)可得，上下支承腔的流量平衡方程式为：

(7)

式(7)中，圆台形滑阀节流器进油量与节流当量间隙三次方成比例，节流器的进油变量指数与支承油腔排油变量指数相当，能够实现快速动态响应。

2.2 支承刚度分析

受到垂直向下的载荷作用时，下承载腔的油膜厚度会减小，上承腔的油膜厚度会增加。支承腔油膜厚度值变化量为e时，滑阀节流器两端液阻Rc1，Rc3及其对应的上下支承腔排油液阻Rb1，Rb3分别为：

(8)

(9)

(10)

(11)

(12)

(13)

支承腔的有效承载面积是Ab，阀芯的端部截面积是Ac，圆台滑阀节流器承载能力为：

W=(pb3-pb1)Ab

(14)

静压支承油膜刚度是指引起单位油膜厚度变化的载荷变动量，受到载荷作用时，油膜刚度为：

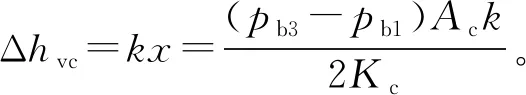
(16)

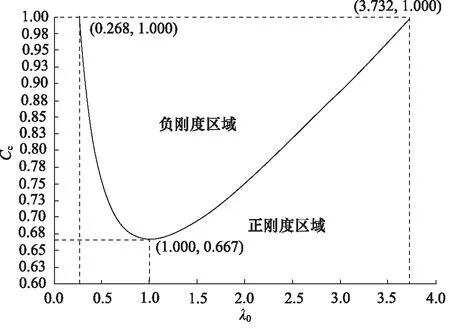
图2 滑阀控制系数与间隙液阻比组合关系曲线

2.3 支承腔油膜厚度分析

阀芯在阀体内会产生轴向位移，设圆台形阀芯两端的初始间隙均为hc0，在载荷W作用下，其在阀体内向压力较低侧位移量为x，则：圆台滑阀两端直径分别调整为dc1=dc+kx，dc3=dc-kx，阀芯两端节流间隙相应调整为hc1=hc0-kx，hc3=hc1+klc=hc0-kx+klc。

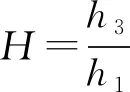
(17)

式中，hvc1，hvc3分别为圆台形滑阀两端节流当量间隙，

=1

(18)

(19)

当载荷W变化，根据不同的n，c取值，计算对应的β值，使n，c与β满足关系式(13)时，支承油腔内的油膜厚度h1，h3基本不会发生变化。c取0.2～0.5，n取2～5，对应计算的β值如表1所示。

表1 不同c，n组合对应的β值

保持支承腔油膜厚度不变的情况下，由表1可知：c值相同，β值的大小随n值正相关变化，说明弹簧刚度一定的滑阀在阀芯位移量相同情况下，阀芯圆台的锥度越大，系统的支承载荷能力也就越大,载荷大小与阀芯圆台锥度正相关；n值相同，β值的大小随c值负相关变化，说明支承载荷一定情况下，要使弹簧刚度一定的滑阀的阀芯位移量越小，阀芯圆台的锥度应当设计的越大，阀芯位移量与阀芯圆台锥度反相关。

3 动态特性分析

实际工况中，载荷是一个动态变量，会使上下支承油腔的径向受力不断变化，需要进一步分析圆台形滑阀节流支承的动态性能。

1) 动态性能数学模型建立

支承件的质量为M，受外载荷作用力大小为W，假定支承件在支承油腔中产生的径向位移量为e，上、下支承腔的支承力分别为F1，F3，则支承件的运动微分方程为：

(20)

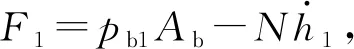
(21)

(22)

(23)

下支承腔油液流量连续性方程：

(24)

支承件在静态位置附近沿径向移动，将hvc1=hvc-kx，hvc3=hvc+kx代入式(3)、式(4)并泰勒展开，忽略二阶及以上各高阶项得：

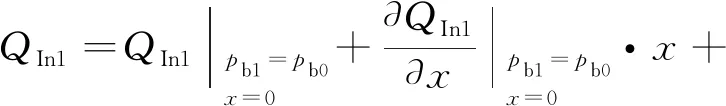
(25)

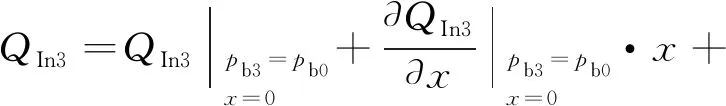
(26)

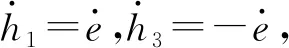
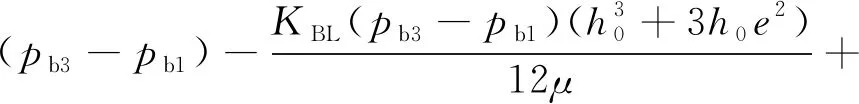
(27)

设pb3-pb0=-(pb1-pb0)=Δpb，pb3+pb1=2pb0，并略去相关高次项可得：

(28)

联立式(21)、式(22)、式(28)得系统微分方程组，为：

(29)

2) 稳定性条件分析

对式(29)进行拉氏变换，得：

(30)

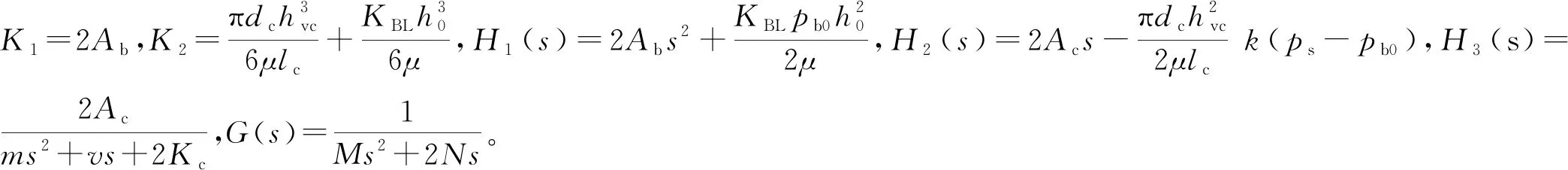
根据方程组式(30)，以径向外载荷W为输入，以支承件的径向位移量e为输出，可得如图3所示圆台形滑阀节流静压支承系统方框图。

图3 圆台形滑阀节流静压支承系统方框图

根据方框图，可得闭环传递函数为：

GB(s)=E(s)/W(s)=G(s)/[1+K1G(s)H1(s)/

(K2+H2(s)H3(s))]

=G(s)(K2+H2(s)H3(s))/[K2+

H2(s)H3(s)+K1G(s)H1(s)]

{K2(ms2+vs+2Kc)(Ms2+2Ns)+

(2μ)](ms2+vs+2Kc)}

(31)

整理得：

G(s)=E(s)/W(s)=(A2s2+A2s+A0)/

(B4s4+B3s3+B2s2+B1s+B0)

(32)

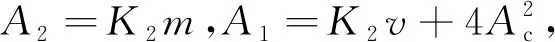
B4=K2Mm+2K1Abm，

B2=2K2(MKc+Nv)+K1[4AbKc+

根据劳斯稳定判据[13]及静压支承系统的特征方程，系统稳定的充要条件是：

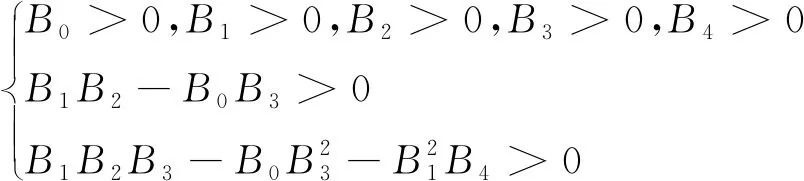
(33)

3) 频响计算分析

支承腔结构、滑阀结构及支承件等参数一定的情况下，取n=3，c=0.4，β=1.17为例，分析圆台形节流器对支承腔油膜厚度影响的幅频特性。图4、图5分别是弹簧刚度系数Kc取1.4， 1.7， 2.0 N/mm及阀芯端部截面积Ac取25.12， 39.25， 56.52 mm2时对应的系统幅频特性曲线，随着弹簧刚度系数的增大或阀芯端部截面积的减小，系统响应的共振幅值减小，油膜厚度变小。图6是圆台锥度k取0.001，0.002，0.004时对应的系统幅频特性曲线，随着圆台锥度的增大，系统共振频率和幅值均升高，且当频率高于一定数值时，不同锥度情况下系统均具有较高的动刚度。

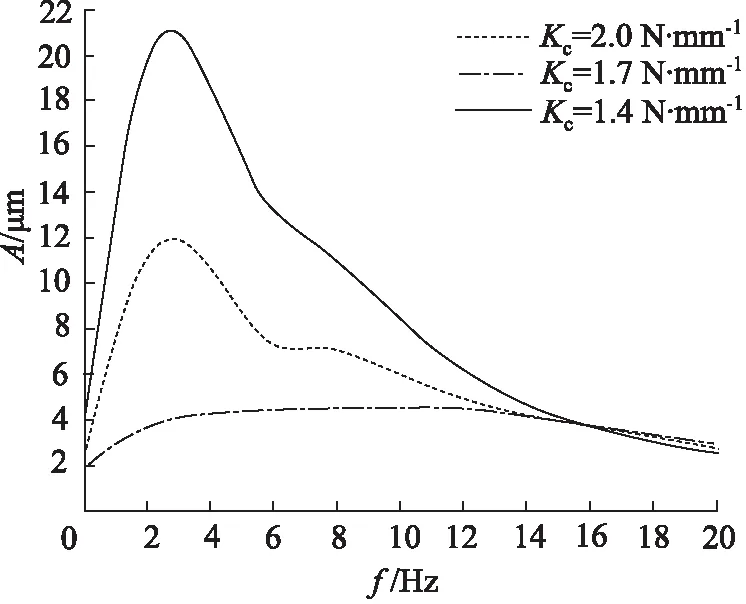
图4 弹簧刚度对幅频特性影响

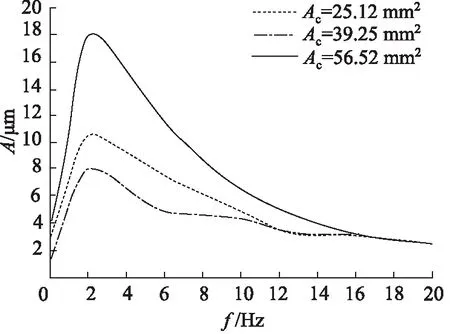
图5 阀芯端部截面积对幅频特性影响

图6 圆台锥度对幅频特性影响

4 结论

(1) 结合静压支承系统需求，设计了一种阀芯是圆台形结构的反馈节流器，该节流器较圆柱形滑阀反馈节流器的动态响应性能更好， 且可克服薄膜型反馈节流器加工难度大、膜片易产生塑性翘曲变形等缺点；

(2) 分析了圆台形滑阀节流反馈静态性能，可按支承腔油膜厚度不变的要求，设计圆台形滑阀节流器相关参数。系统载荷n值确定后，选择适当c值，并从表中选定β，由c，β可以求出弹簧刚度系数Kc及圆台锥度k；

(3) 分析了圆台形滑阀节流反馈动态性能，在静态参数范围内，选择较小的阀芯截面积、较小的圆台锥度或较高的弹簧刚度，可改善支承系统动态响应性能，降低受载荷作用产生的油膜厚度。