QMEMS 陀螺标度因数温度补偿方法研究

张琬琳

（无锡商业职业技术学院 物联网技术学院， 江苏 无锡 214153）

0 引 言

惯性测量单元（Inertial Measurement Unit，IMU）传感器用于测量运动体的运动姿态并广泛应用于航空、航海以及陆地导航领域[1-2]。MEMS（micro-electro-mechanical system，微机电系统）技术的发展推动了微惯性器件和IMU 技术的发展，新一代微机械惯性传感器（MEMS IMU）应运而生。石英音叉微机械陀螺仪又称为QMEMS 陀螺[3-4]，受加工工艺限制，其系统输出误差较大，使惯性导航系统的精度降低。标度因数表示陀螺仪输出量与输入角速度的比值，直接影响着QMEMS陀螺的动态输出。理想情况下，标度因数应为一恒定系数，但由于QMEMS 陀螺内部各元器件具有温敏特性，标度因数会随温度发生变化。为研究标度因数温度补偿的有效方法，有研究者建立了温度变化引起的陀螺标度因数误差漂移模型，从软件方面对误差建模分析以寻求有效的补偿方法。针对陀螺温度漂移模型，罗超等[5]提出用BP 神经网络描述陀螺的随机误差的温度特性，但未对陀螺的标度因数进行非线性建模；席绪奇等[6]提出基于多项式模型和BP 神经网络的光纤陀螺温度补偿法，即应用BP 神经网络处理由温度引起的陀螺零偏误差，采用多项式模型处理标度因数的非线性问题。由于多项式模型属于线性估计，回归的关联式不能全部通过每个回归数据点，因此模型的建立存在一定的局限性。本文采用BP神经网络对QMEMS 陀螺的标度因数温度特性进行建模，并与最小二乘法构成的多项式模型进行对比，研究不同方法对QMEMS 陀螺标度因数温度补偿的效果。

1 最小二乘法

2 人工神经网络

人工神经网络通过对信息分布存储和并行协调处理来模拟人类思维，多层前馈网络又称为BP（Back propagation）神经网络，其学习规则主要包含原始信号的正向传输和误差的反向修正两方面，一般由输入层、隐含层和输出层组成，多层前馈网络示意如图1。

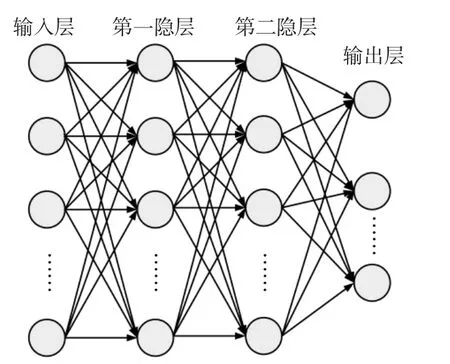
图1 多层前馈网络示意

假设三层BP 网络，输入节点pj，输入神经元有R 个，隐层节点a1i，隐含层内有S1个神经元，传递函数为f1，输出节点a2k，输出层有S2个神经元，输出层传递函数为f2，输入节点与隐层节点的网络权值为w1ij，隐层节点与输出节点间的网络权值为w2ki，当输出节点的期望值为tk，模型的计算过程如下。

2.1 信息的正向传递

2.2 利用梯度下降法求权值变化误差的反向传播

3 根据测试数据进行标度因数拟合

QMEMS 陀螺具有体积小、结构简单、可靠性高、成本低的特点，其主要工作部件是石英音叉以及激励电路和感测电路，结构原理如图2 所示。

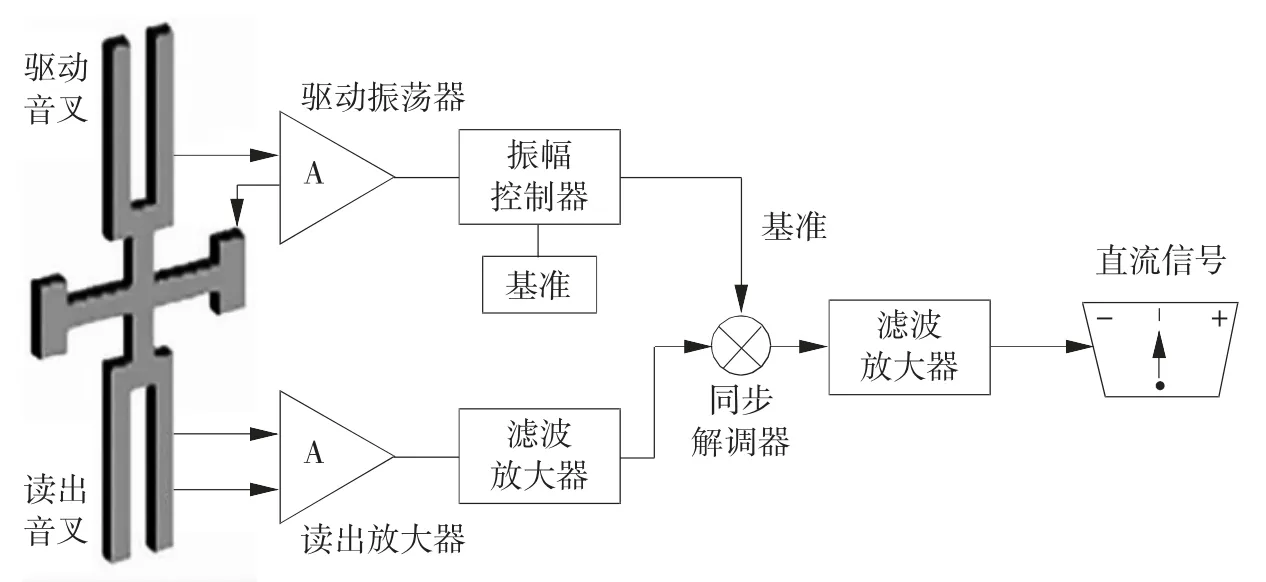
图2 QMEMS 陀螺结构原理框图

为研究温度对QMEMS 陀螺标度因数的影响，分别在-40 ℃~70 ℃环境温度下，以10 ℃为增量对IMU 系统进行高低温测试，每一温度点重复测试三组数据。温度测试使用MAXIM 公司产的DS1820 数字温度传感器，提供9 位（二进制）温度读数指示器件温度。DSl820 的测量范围为-55 ℃~+125 ℃，增量为 0.5 ℃，可在 l s（典型值）内将温度信号变换成数字显示。

表1 为系统X 轴QMEMS 陀螺标度因数随温度变化的实际测量结果。以表1 原始数据为输入，分别利用不同方法进行拟合[5-6]，并建立模型加以补偿。

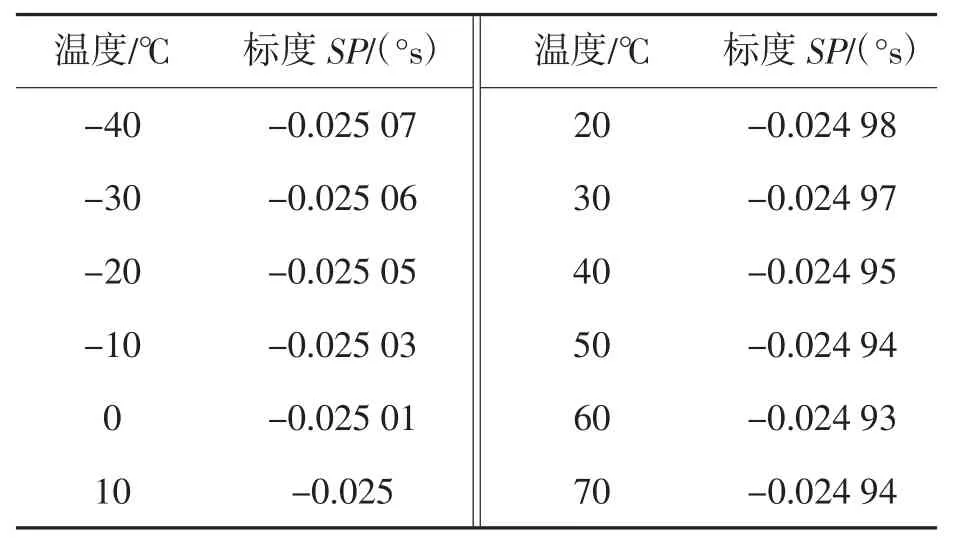
表1 X 轴不同温度下的QMEMS 陀螺标度因数

对X 轴标度因数分别采用一阶最小二乘法进行拟合，可得到标度与温度关系：

其中，T 表示陀螺体当前温度，F（T）为当前温度下的标度因数。应用二阶最小二乘拟合，可得到标度与温度关系：

根据系统要求，建立如图3 所示的1-3-1 神经网络模型，模型中将温度作为输入P，输出a2为待拟合的标度因数。

网络的仿真和训练在Matlab 环境下运行，按照图3 所示补偿模型设置：

图3 神经网络结构

经训练后需提取的参数为w1（3×l），w2（1×3），b1（3×l），b2（1×l）。

图4 为200 步的训练过程中的误差收敛曲线，图5 为仿真误差曲线。

图4 训练过程的误差收敛曲线

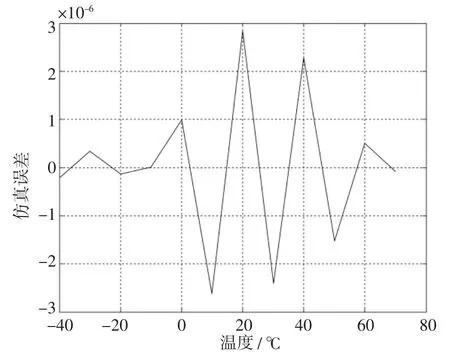
图5 神经网络的仿真误差

经训练后得到参数：

通过式（17）即可进行补偿解算，

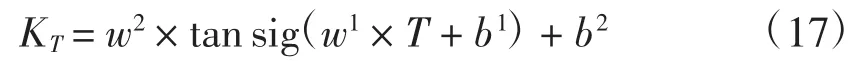
其中，T 为温度，KT为温度模型补偿输出的标度因数，tan sig 函数的解析式为：

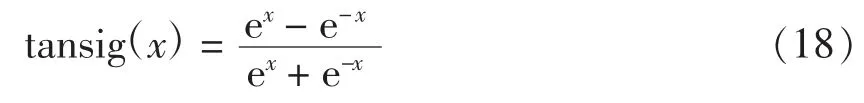
图6 为不同方法的温度补偿拟合结果，图中温度为横坐标，陀螺标度因数为纵坐标。表2 为针对QMEMS 陀螺标度随温度变化的曲线拟合参数比较结果。由图6 和表2 结果可以看出，神经网络法拟合效果明显要优于线性拟合法与最小二乘曲线拟合法。

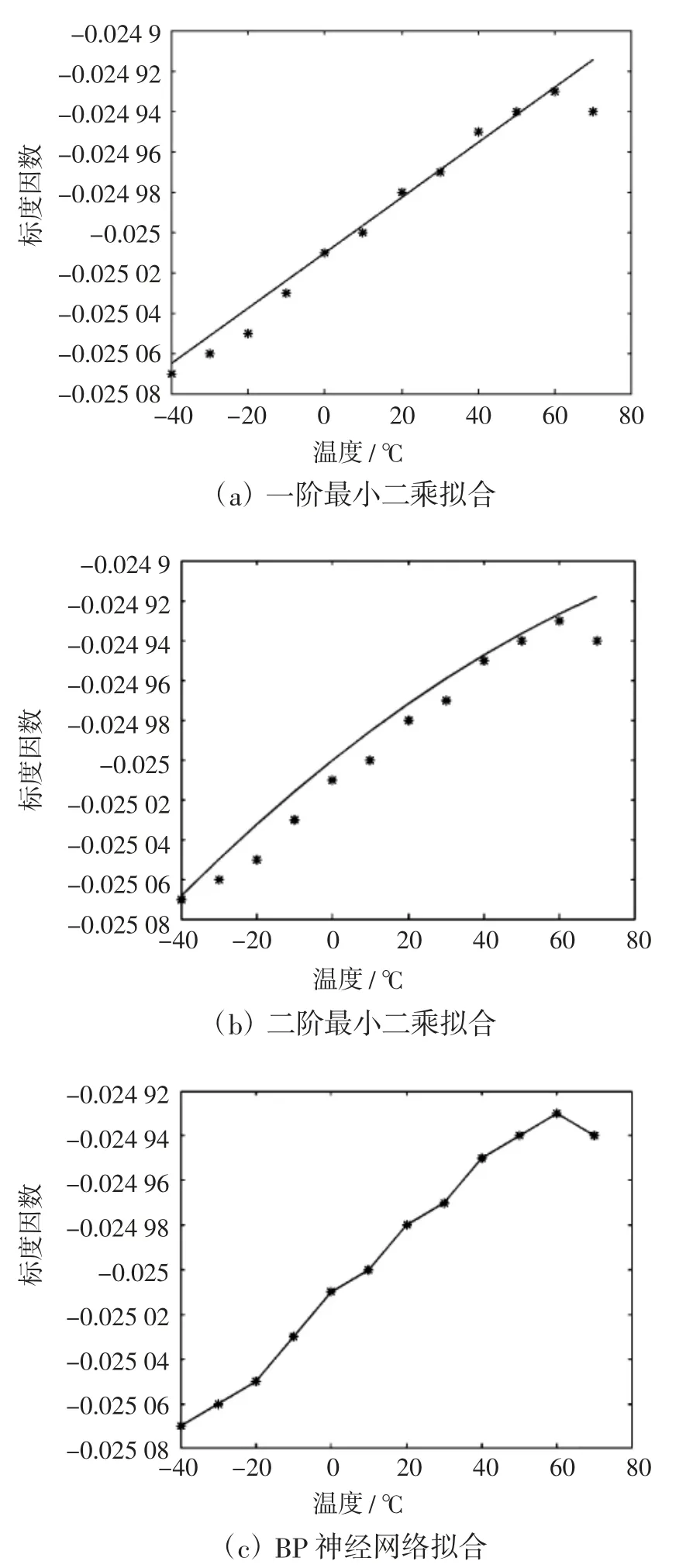
图6 不同拟合方法的拟合效果比较

表2 三种补偿方法误差比较

4 结 语

将神经网络算法应用于QMEMS 陀螺标度因数的温度补偿，并与最小二乘法进行对比分析。结果表明，神经网络算法可对温度变化引起的标度因数误差进行有效补偿。仿真计算可见，神经网络算法计算量较大，且需一定的数据支持。因此，如何提高算法的实时性，使算法能够适用于工程应用，还有待进一步研究。