因子分析法在城市人才吸引力综合评价中的应用——以广东省部分城市为例

周 蕾

（广州科技职业技术大学 基础部， 广州 510550）

当今世界，人才已成为各国经济发展、社会进步和增强国家竞争力的基础和关键，人才资源也是城市现代化建设的第一资源。因此，关注人才的生活、科研、工作和发展需求，科学地分析吸引人才的各种因素，是制定和完善人才吸引力政策的重要环节。本文拟运用因子分析法建立模型，找出多个变量的公共因子及其贡献率，定量评价城市对人才的吸引力，并以广东省为例，对各城市的人才吸引力进行综合评价。

1 评估指标体系与观测变量的选择

建立人才吸引力的评价指标体系要遵循系统性、导向性、直接性和客观性四个原则，做到设置尽可能全面，指标选择要有直接影响、可测、量化，并确保可信度。

按照上述原则选择人均GDP、城市GDP、进出口贸易总额、经济结构、旅游业总收入、医疗机构数量、工业增长值、房地产业开发投资、平均工资、居民人均可支配收入、就业人数等11 个指标，构成能综合反映城市人才吸引力水平的指标评价体系。选择深圳、广州、东莞、中山、肇庆、汕尾、珠海、汕头、佛山、河源、梅州、惠州等12 个广东省的主要城市，针对上述11 个指标，从2019 年《广东社会统计年鉴》和《广东统计年鉴》提取原始观测数据，获得12 个样本xj=（x1j，x2j，…，x11）jT，设其中的数据xij均已作标准化处理（1≤i≤11，1≤j≤12），则构成一个 11 × 12 的数据矩阵X=（xi）j11×12=（x1，x2，…，x12）。

2 模型的基本原理

多个变量分析时，往往由于指标过多，增加了复杂性，掩盖了关键点。在实际问题中，指标间通常具有一定的相关性，因此统计分析时希望用较少的关键指标代替众多指标，但要尽量不损失原有信息。因子分析法[1-2]是一种从众多变量中提取共性因子的多元统计方法，即将比较密切相关的几个变量归于同一类，每一类变量成为一个因子进行统计。这种化繁为简的处理，能以较少的因子刻画原资料的大部分信息，体现了决策中的关键性和代表性，便于突出主要矛盾，把握全局。

以数据矩阵X 为起点，求出其相关矩阵R=XXT的相似对角阵 Λ =diag {λi}1≤i≤11和特征向量矩阵U=（uji）T11×11。其特征值按λ1>λ2>…>λ11≥0排列，U 是正交矩阵。记 B = UTX =（UTx1，UTx2，…，UTx12）=（p1，p2，…，p12），则有

模型将原来11 个观测变量表示为尽可能小的m（<11）个公共因子的线性组合，使结构简单而合理。原观测变量在某一主因子上的载荷，由该主因子对应的特征向量确定。

3 模型的求解

运用SPSS 软件进行因子分析，主要原理是主成分分析与因子旋转。具体步骤如下：（1）将变量标准化；（2）通过相关矩阵判断是否能对变量进行降维处理；（3）利用主成分分析法对初始因子载荷矩阵进行估计；（4）根据显著性水平，用特征值之和与矩阵迹的比来确定公共因子的个数，或者用因子累计方差贡献≥85 %来判断公共因子个数；（5）如果初始因子载荷矩阵不能很好地解释，用最大方差法对因子荷载矩阵进行正交旋转；（6）对公共因子进行命名；（7）计算因子得分；（8）以方差贡献率为权重建立综合评价模型；（9）排序。

3.1 巴特利特球形度检验

首先，通过KMO 和巴特利特检验[3-4]来判断数据是否适合进行因子分析。表1 的计算结果说明，数据之间存在相关性，适合进行因子分析。

表1 KMO 和巴特利特检验结果

3.2 公因子方差

在使用SPSS 软件时，公因子方差表中的“提取”一栏中的值越大，说明变量可以被公因子表达的信息越多，效果越好。表2 中“提取”的值均大于0.7，故本文所选的11 个变量可以被充分表达。

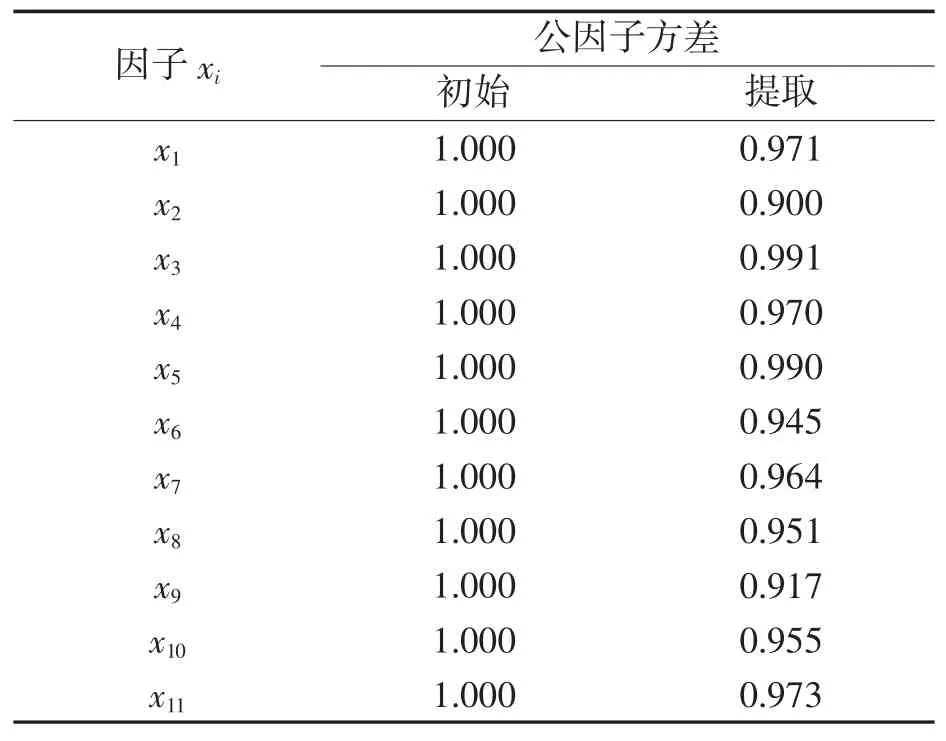
表2 公因子方差

3.3 因子分析

表3 给出了各因子的特征值及贡献率。根据累计贡献率，取4 个公共因子已能反映原始数据95.71%（>80 %）的信息，将其作为反映原指标的信息量可认为是有效的，即原11 个指标可综合成4 个公共因子。其中，第一个公因子解释的方差最大，为8.333，说明该公因子所占比重最大。

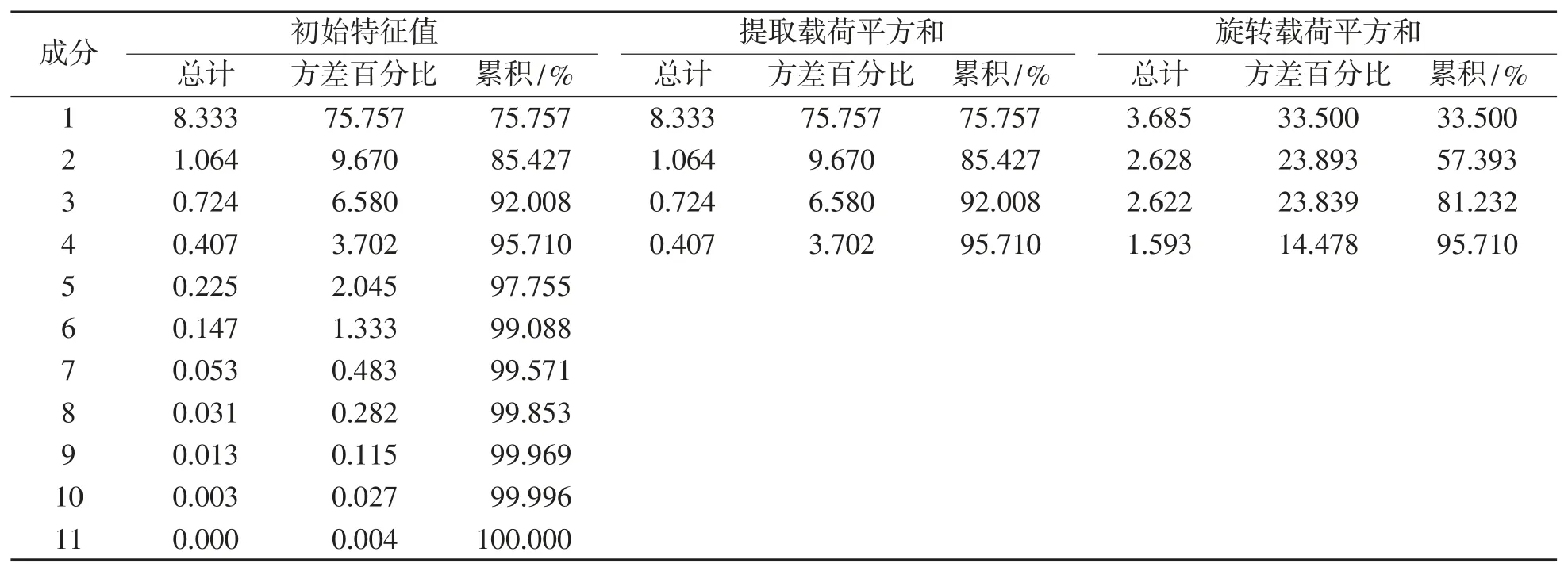
表3 总方差解释

表4 分别给出了旋转前后的因子载荷矩阵[5]，其中，由旋转前的因子载荷矩阵中第一公共因子的相关数据对11 个变量中大部分变量都有较明显的影响作用。由此看出，因子变量的含义还比较模糊，不利于对因子的实际背景进行合理解释，需要进行因子旋转。利用最大方差法进行因子旋转。从旋转后前4 个公共因子的因子载荷矩阵可以发现，数据明显向0 或1 两极方向分化，这将有利于对公共因子进行解释。

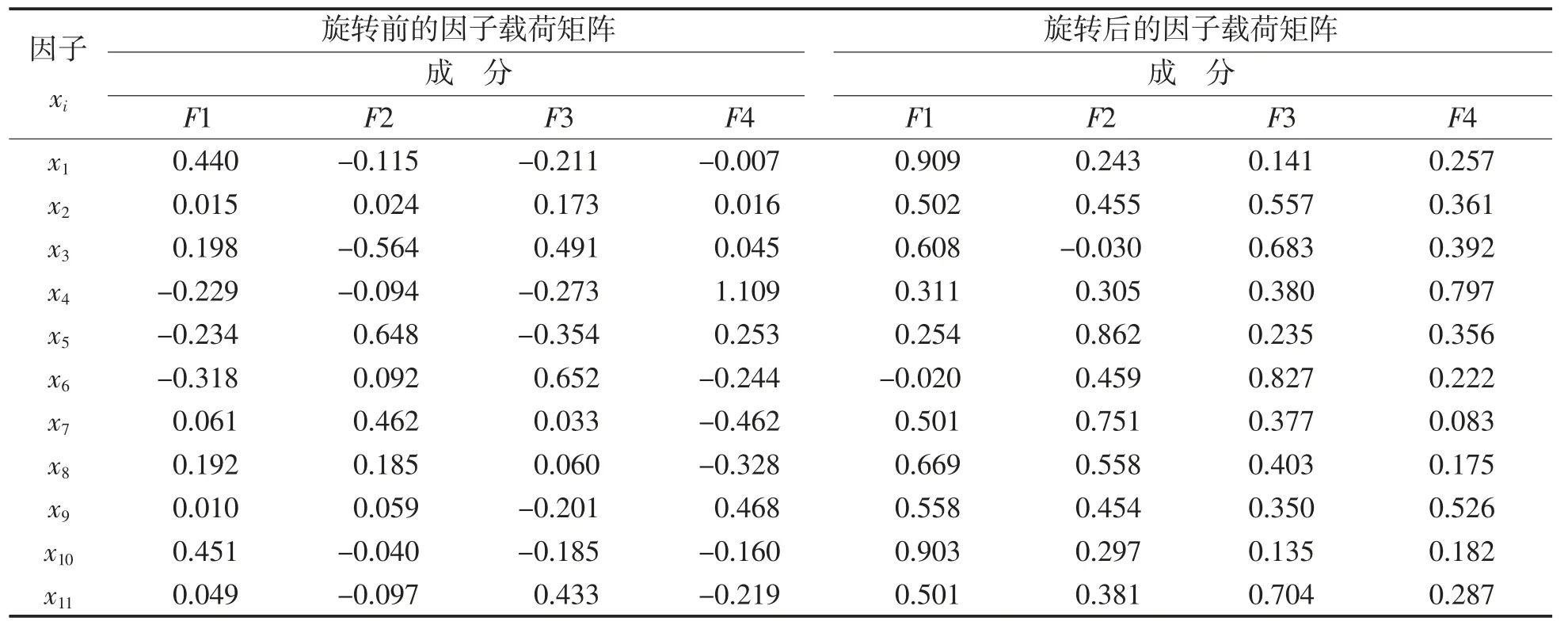
表4 旋转前后的因子载荷矩阵

通过对旋转后的因子载荷矩阵分析可知，F1在人均GDP、进出口贸易总额、房地产开发投资和居民人均可支配收入中的值较大，说明F1 在这几个变量中有较大的载荷。F2 在旅游业总收入、工业增长值中的值较大，F3 在医疗机构数量中的值较大，F4 在第三产业占比中的值较大，这些同样说明F2、F3、F4 分别在这几个变量中的载荷较大。可见，F1 更多表示的是各个地区的经济发展情况，命名为经济发展因子；F2 表现的是各个地区行业的发展状况，命名为行业发展因子；F3 反映的是各个地区的基础设施、保障民生的情况，命名为民生基础因子；F4 则反映了各个地区的产业结构，命名为产业结构因子。

3.4 综合分析

根据上述4 因子模型，在广东省选取12 个城市进行人才吸引力综合分析与评价，以表3 中4个公因子对应的方差贡献率为权数，通过下式计算综合因子得分并进行排名，结果如表5。

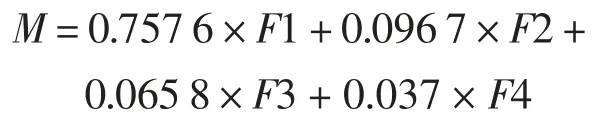
其中，M 表示人才吸引力总得分，F1、F2、F3、F4 分别表示4 个公共因子的得分。

由表5 可见，深圳作为最早实行对外开放的经济特区之一，发展势头迅猛，在经济发展因子、民生基础因子、产业结构因子三方面都走在所选取的12 个城市前列，对人才吸引力最大。广州在行业发展因子方面比较好，同时，东莞、佛山、珠海这些处于珠三角地区和粤港澳大湾区的城市，对人才的吸引力也非常大；汕头作为老牌经济特区的人才吸引力也并不弱；梅州、河源、中山等市地理位置不占优势，城市人才吸引力非常弱。

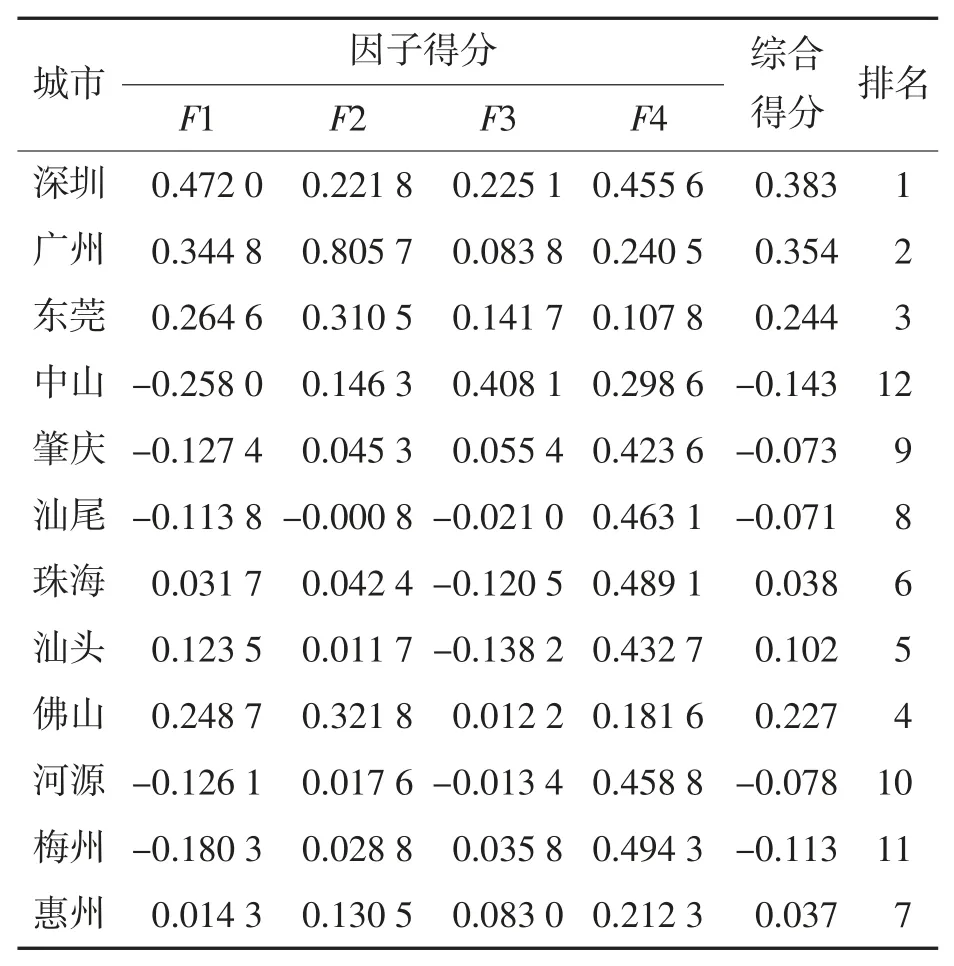
表5 所选12 个城市人才吸引力因子分析综合得分及排名

4 结 语

上述因子分析表明，经济发展因子的贡献率高达75.76 %，可知城市的经济发展现状和潜力对人才吸引力的影响最为显著。人才吸引力评分第一的深圳，从改革开放至今，经济发展势头一直很强，在粤港澳大湾区发展带动下，作为建设中国特色社会主义先行示范区，经济发展更是势不可挡，对人才的吸引力也是越来越大。对比其他城市，深圳作为高新技术聚集的城市，其旅游业和工业等发展相对较薄弱，这将导致深圳的人才吸引因素单一化。大量的高新技术人才涌向深圳，而一些服务业需要的劳动力资源得不到满足，从而影响深圳的全面长远发展。通过分析不难发现，国家政策对城市经济发展作用重大，很大程度上影响着城市的人才吸引力。改革开放政策让一些沿海城市得到飞速发展，因此，人才更愿意涌向沿海城市。基础建设、产业结构等更能体现一个城市的竞争力，深圳在这些方面均有领先优势，因此其人才吸引力也领先于所选取的其他11 个市。由于我国各省市统计数据指标大体相同，本文方法也适用于全国其他城市间的分析比较。选取不同的指标变量，还可用于分析比较各城市其他方面的发展情况，如城市环境保护、绿色经济发展等。