基于混合智能算法的随机共振微弱信号检测

郑文秀，文心怡，杨 威，姚引娣

(西安邮电大学通信与信息工程学院，陕西西安 710121)

1 引言

信息时代需要各种各样的信息，其中人们取得信息的一个必要方法是微弱特征信号检测[1]。微弱信号检测作为一门综合学科，需要充分利用电子学、信息理论、非线性科学、信号处理及计算机技术研究噪声产生的原因，且要根据不同的实际问题用不同的方法来检测淹没在强噪声背景中的微弱信号。弱信号检测是研究如何从被强噪声淹没的混合信号中检测出或者提取出有用信号的一种技术[2]。

在实际信号处理中，噪声，例如来自系统的固有噪声和外部环境的干扰等，是不可避免的。它经常与有用信号混合，这使得有用信号难以识别并提取。当信号被送入非线性系统时，输出信噪比并没有下降，而是通过增加噪声来改善。因此，Benzi提出了随机共振(Stochastic Resonance)的概念[3][4]。1983年，Fanve和Heslot研究依赖于噪声的交流驱动施密特触发器的功率谱证实了随机共振现象[5]。在20世纪90年代初期，Collins将随机共振与信号处理相结合提出了非周期随机共振理论[6]。随后，随机共振被广泛应用于雷达，声纳，图像处理，语音识别等领域。Hari等人设计了一个基于阈值的随机共振探测器，用来提取埋藏在非高斯噪声中的确定性信号[7]。

然而，由于参数的依赖性，参数设定的原理成为重要的研究话题，因此提出了一些自适应算法来选择随机共振参数。Lei等人使用蚁群算法来同步选定和优化随机共振参数[8]，该方法通过仿真成功提取了齿轮箱故障信号中的弱故障信号，同时获得了故障严重程度。行鸿彦等人提出使用全局人工鱼群算法来优化随机共振多参数并行寻优的问题[9]。焦尚彬等人提出采用基于知识的粒子群算法来实现并行优化随机共振系统结构参数[10]。

本文利用人工鱼群算法与粒子群算法相结合的方法，将随机共振输出信噪比作为目标函数。回避粒子群算法调参的过程中极易导致局部最优的问题和人工鱼群算法后期搜索不精确的不足。采用MATLAB仿真平台，将待测信号输入到自适应系统当中，优化系统参数，实现微弱信号的检测。

2 随机共振模型

2.1 随机共振原理

Duffing随机共振双稳态系统的发生载体为Duffing混沌振子。广义的Duffing方程是在方程等号的右边加上了噪声与外部周期驱动力。具体形式为

(1)

(2)

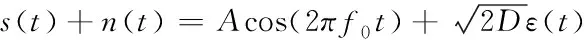
(3)

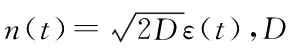
图1 Duffing 随机共振双稳态系统模型

当噪声和微弱周期信号同时作用于随机共振系统，噪声、信号以及非线性系统三者达到某种匹配关系时，合理调节切换速度使输出信号与微弱周期信号趋于同步，从而使随机共振检测到微弱信号。

2.2 信号的目标优化函数

在实际工程中，常会出现在强噪背景下多个频率的微弱信号叠加的情形，当多频周期信号为输入信号时，根据式(2)可得

(4)

式(4)中，fi和Ai分别为第i路的信号频率和幅度。为了智能算法准确地寻找到随机共振的最佳参数组合，需提供一个多频率目标优化函数。本文以平均输出信噪比作为算法的适应度函数，定义如下

Fitness(a，b，c)=(SNR1+SNR2+…+SNRn)/n

(5)

式中：n为信号个数，SNRi，i=1，2，…，n代表第i个信号的输出信噪比。

令采样点数为N，采样频率为fs，将含有噪声的多频率微弱信号和输出信号作快速傅里叶变换后，可以计算出系统第i个周期信号的输入和输出信噪比。公式如下

SNRi=

(6)

综上，根据(5)和(6)式，多频率优化函数可以表示为

Fitness(a，b，c)=

(7)

式中，fi为第i个周期信号在频谱中对应的位置点，可以用下式计算

kfi=round((fi/N)*fs+1)

(8)

信噪比在随机共振中有很重要的角色。其定义为：输出信号功率谱中信号频率的幅值与同频背景噪声之比[16]，表达式为

(9)

式(9)中：S(ω)代表信号功率谱密度；噪声在信号频率附近的强度大小用SN(ω)表示。需要注意的是，此处的信噪比是局部范围内的信噪比。在随机共振系统中，信噪比与噪声强度两者是非单调关系，并且在一定的噪声强度时出现一个峰值。

3 混合智能算法

3.1 人工鱼群算法原理

人工鱼群算法(AF)是一种模拟鱼类行为的优化方法[12]，该算法通过效仿鱼群的生存行为在搜索域中实现全局寻优[13]。通常，鱼群行为有觅食、聚群、追尾等。

假设X=(x1，x2，…，xn)，其中的xi(i=1，2，…，n)代表准备优化的变量；Y=f(x)代表当前人工鱼的食物浓度，visual规定了鱼类的感知范围；δ是拥挤度因子的含义；V代表视野范围；L为移动步长；在觅食行为中try_number描述了最大的尝试次数。如果人工鱼i的状态位置为Xi，那么相应地Yi为其食物浓度。

3.2 粒子群优化算法原理

粒子群优化(PSO)是一种仿生优化算法，它模拟社会行为，例如鸟类都飞向对自己最有利的位置，以便精确获取目标[14]。PSO根据每个粒子和整个群体(称为群体)获得的适应度信息来更新当前一代个体(称为粒子)。其中，pbest和gbest分别称为认知部分和社会部分。

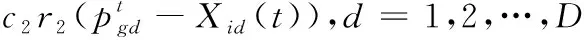
(10)

Xid(t+1)=Xid(t)+Vid(t)，d=1，2，…，D

(11)

式(10)中，c1和c2分别为认知学习因素和社会学习因素；ω代表惯性权重；r1和r2设置为[0，1]区间的随机数。

3.3 混合智能算法原理

人工鱼群算法只能找到满意的可行解，很难求得最优解。粒子群优化算法容易陷入在局部最优解。将两种算法相结合，根据前者的全局收敛性快速搜索到满意的解域， 再利用后者进行快速的局部搜索，找到随机共振最优参数a、b，这样混合后的算法不仅具备全局收敛性能，还保证了快速的局部搜索能力[15]。

基于混合智能算法的自适应调参随机共振信号检测具体流程如图2所示。

图2 基于智能算法的自适应随机共振信号检测流程

算法主要步骤如下：

1) 输入待测信号和噪声强度。

2)初始化鱼群以及算法参数。

3)评价鱼群各条人工鱼的食物浓度。针对微弱信号检测，目标函数设置为随机共振输出信噪比。公告牌里保存最优人工鱼的信息

4)鱼群进化更新。各条人工鱼根据鱼群行为判断条件选择具体的行为执行，并实时调整公告牌信息。

5)人工鱼群算法终止条件判断。若满足设定的算法结束条件，将最优值、最优位置更新于公告牌，转步6)，否则转3)。

6)粒子群初始化。将人工鱼群算法终止时每个个体信息对应赋值给粒子群种群。将公告板最优位置、最优值信息赋给pbest和gbest。

7)计算每个粒子的适应度。将随机共振输出信噪比作为适应度函数，计算粒子的适应度。

8)粒子群进化更新。

9)粒子群算法终止条件判断。若满足则输出最优解，算法终止，否则转7)

10)输出全局最优粒子gbest(a，b，k的值)的信息，将优化后的参数输入Duffing 随机共振双稳态系统，实现微弱信号自适应随机共振检测。

4 实验结果与分析

4.1 多频微弱周期信号检测

对强噪声背景下的多个小频率微弱周期信号，智能调节双稳态随机共振参数a、b，将随机共振平均输出信噪比作为共振测度指标和目标优化函数。

将待测的三个正弦信号输入到式(4)当中。混合信号的幅度分别为A1=0.01、A2=0.15、A3=0.20，对应的信号频率分别为f1=0.01Hz，f2=0.03Hz，f3=0.05Hz，采样频率取为4.098Hz，采样点数N=4096。此时n=3，n(t)的噪声强度为1。信号波形无周期特征，待测信号完全被强噪声所淹没，根据式(9)系统的输入信噪比为-18.2391dB。

采用粒子群算法自适应调节双稳系统，系统参数设置如下：学习因子c1、c2都为2；种群规模M=60；惯性权重ω=0.5；系统参数a、b的寻优范围为[amaxmin]和[bmaxmin]，这里取aminmin=0.001，aminmin=2.500。

优化后的结果分别为：a=1.6594，b=1.9782。输出信号和功率谱如图3所示。系统输出信号显现一定的周期性，信号频谱在频率点f3=0.05Hz处有较大的频谱值，但待测信号频率f1=0.01Hz、f2=0.03Hz附近噪声干扰较多，有些频率不能准确地检测出来。

图3 基于粒子群算法的多频微弱信号检测输出信号时频图

人工鱼群算法是另外一种自适应调节算法，算法的参数设置如下：

种群规模M为60；视野范围V为3；人工鱼步长L=0.02；尝试次数try_number=60；鱼群迭代次数60；拥挤度因子δ=0.618；除此之外，参数范围a、b设置与PSO和SAPSO算法同样。寻优结果为a=0.010、b=0.010。寻优后的信号波形及频谱输出结果如图4所示。

图4 基于人工鱼群算法的多频微弱信号检测输出信号时频图

从图4信号波形图可以看出，输出时域信号周期性已经十分明显，多个待测信号的幅值放大显著，说明有一部分噪声能量转移到了待测信号频率上。f1=0.01Hz，f2=0.03Hz，f3=0.05Hz频率处分别位于三个谱峰值上，但零频附近峰值附近噪声毛噪较多。

以混合智能算法为参数调优算法，对多频率微弱信号进行自适应检测。

采用Runge-Kutta算法求解二维Duffing振子随机共振方程，由于发生随机共振时a，b取值范围小，为了算法效率的提升考虑，同时基于PSO算法和人工鱼群算法的参数，设置混合智能算法参数如下：种群规模 M=60，V=3，L=0.02，尝试次数try_number设为60，鱼群迭代次数40，粒子群迭代次数20，拥挤度因子δ=0.618。共振参数是与上述算法取值一样的。经过60次的迭代和运行，得到优化后的参数a=0.7696、b=0.2569运行结果如5所示。

图5信号频谱图利用混合智能算法优化参数的随机共振输出信号得到了较前两者更高的谱值，也更突出，因此更有利于微弱信号的检测。实验结果表明混合智能算法明显提高了调参准确度，极大改善了随机共振的信号检测效果[17]。

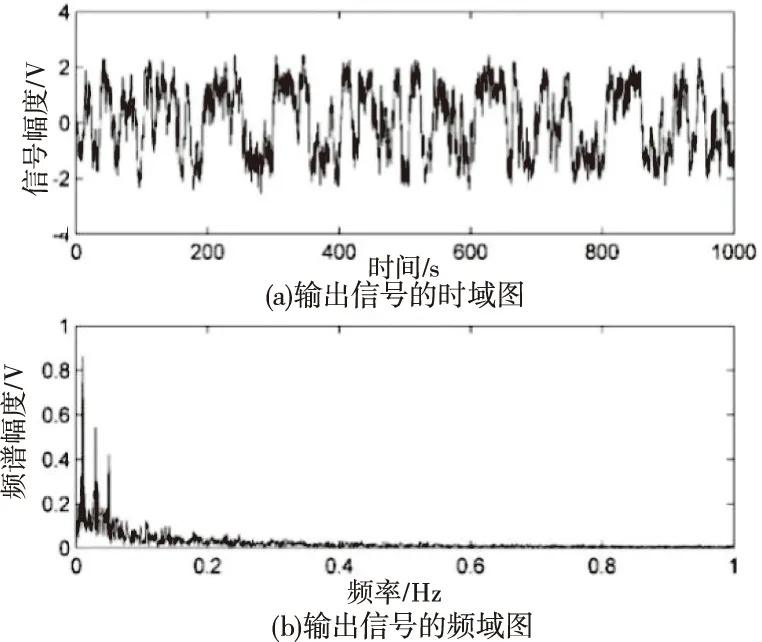
图5 基于混合智能算法的多频微弱信号检测输出信号时频图

4.2 单频率微弱周期信号检测

令待检信号u(t)=Acos(2πf1t)+n(t)，其中周期信号幅值A=0.5，频率f1=0.1Hz，n(t)是均值为零，噪声强度D为12.5的高斯白噪声；以单频率目标优化函数即输出信噪比为测度指标。

取采样频率fs=20Hz，数据长度N=2000。此时输入的信噪比为-20dB。

分别使用PSO算法、人工鱼群算法、以及混合智能算法自适应地调节双稳态系统参数，以输出信噪比为测度指标，依次用MATLAB仿真单频率微弱信号的检测。每种算法参数设置与多频率微弱信号的对应算法参数统一，仅仅更换了测度指标，测度指标由多频目标优化函数变为单目标优化函数。各算法的输出信号波形及功率谱分别如图6、7、8所示。

图6 基于粒子群算法的单频微弱信号检测输出信号时频图

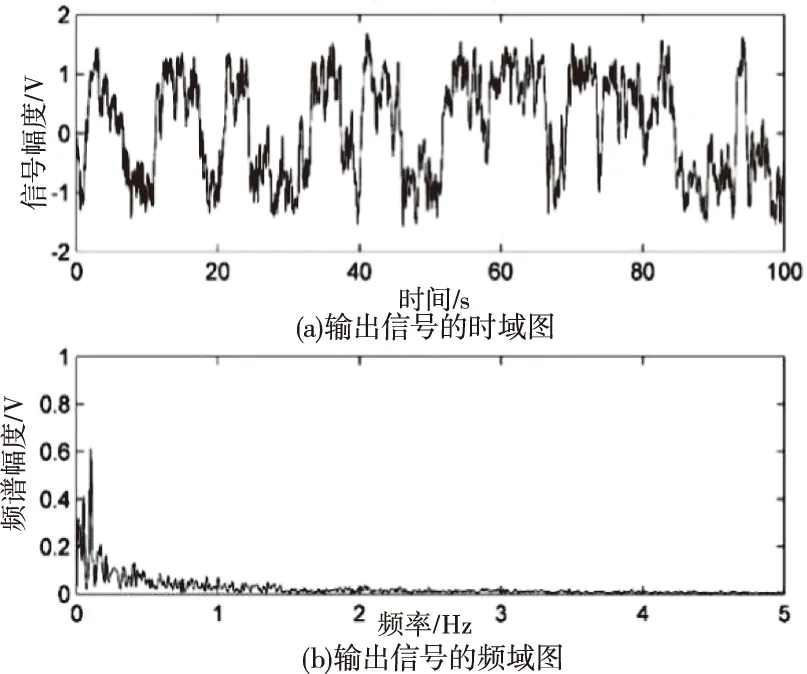
图7 基于人工鱼群算法的单频微弱信号检测输出信号时频图

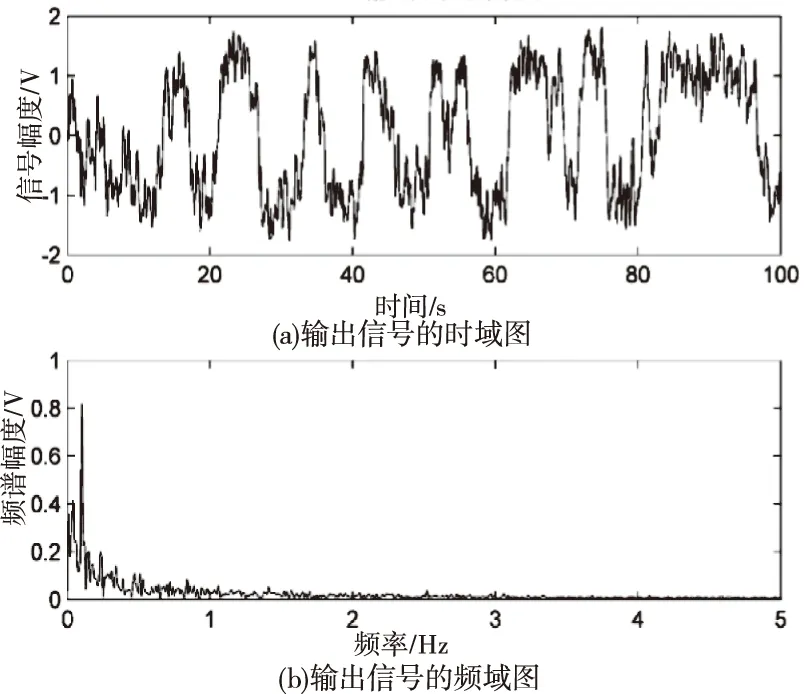
图8 基于混合智能算法的单频微弱信号检测输出信号时频图

各算法的参数优化结果如下所示：

粒子群算法：a=0.0619、b=0.2496；自适应粒子群算法：a=0.0253、b=0.3481；人工鱼群算法：a=1.5182、b=1.0501；混合智能算法：a=0.1208、b=0.2768。

图6中，粒子群调参的信号频谱中目标信号频率为0.1Hz附近受噪声影响大，待测信号的频谱的凸显并不明显，难以判断出目标信号的频率；图7中人工鱼群调参的效果较粒子群有所提高，算法的效果明显。利用混合智能算法优化参数的随机共振输出信号谱值最高，待测信号频率处谱线更突出，因此有利于微弱信号的检测[17]。

5 总结

本文通过分析常见的两种智能算法的优缺点，引入了一种新的人工鱼群与粒子群混合智能算法。最后，在高斯白噪声背景下，讨论了单频率和多频率微弱信号的测度指标，在给出的测度指标的基础上，运用几种智能自适应算法分别调节双稳态随机共振系统参数，其中着重研究混合智能算法检测多频率微弱周期信号的情况。仿真结果表明，混合智能算法可以在强噪声背景下快速而有效地检测出含有多个频率或者单个频率的周期信号；同时，通过对比试验数据，可以看到混合智能算法比列举的其它算法准确性高、工程实用性强。