考虑釉面膨胀系数的陶瓷表面微裂纹扩展模拟

李 营，许晓政 ，甄照旭，隋 多

(1. 沈阳理工大学，辽宁 沈阳 110159；2. 辽宁师范大学网络信息管理中心，辽宁 大连116029)

1 引言

粘土和天然矿物质等通过粉碎烧制而成的用品、器具等统称为陶瓷，其具有较高使用价值和观赏价值[1]。现代陶瓷不仅在质量上有所提升，也在艺术领域占有一席之地，因此，陶瓷器具的外观具有艺术性、个性化等特点[2]。

陶瓷在制作过程中，釉面产生的微裂纹现象称为“开片”。对于艺术性陶瓷器具来说，“开片”可作为一种装饰，提升陶瓷的艺术性，但对于日常使用的陶瓷器具来说，“开片”会影响其使用寿命。当釉面的膨胀系数高于胎的膨胀系数时，陶瓷就会发生“开片”现象[3]。膨胀系数是形成陶瓷“开片”现象的原因之一。膨胀系数是表征物体热膨胀性质的物理量，即表征物体受热时其长度、面积、体积增大程度的物理量，陶瓷表面微裂纹的扩展受膨胀系数影响较大[4-5]。

工业陶瓷材料生产过程极为复杂，有效把控陶瓷材料表面微裂纹的产生，减少陶瓷材料的损耗，提升陶瓷材料加工质量，是国内外许多学者专家极力解决的难题[6]。解决陶瓷表面微裂纹扩展问题不仅可提升陶瓷质量，而且可提升陶瓷器具或零件的可靠性，是陶瓷产业研究的主要方向之一。为此，本研究从影响陶瓷微裂纹扩展因素之一的釉面膨胀系数为出发点，构建数值模型对陶瓷表面微裂纹扩展进行模拟。

2 陶瓷表面微裂纹数扩展模拟设计

2.1 裂纹应力强度因子

假设釉面为陶瓷基体材料中所包裹的球状颗粒，利用数学处理可将球形颗粒半径逐渐趋向于无穷大过程中的情形模拟演变成陶瓷材料与釉面垂直的表面微裂纹的应力强度因子[7]，球状颗粒两侧陶瓷微裂纹如图1所示。

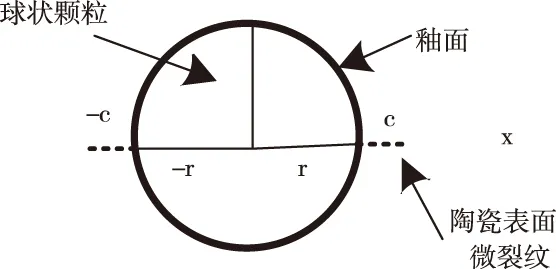
图1 球状颗粒两侧陶瓷微裂纹

(1)

(2)

σ12(x，0)=0

(3)

式中，陶瓷材料的剪切模量由F1表示，陶瓷材料的泊松比由e1表示。

当应力足够大且颗粒满足0<σ22(x，0)，会导致颗粒两边外侧陶瓷向内出现微裂纹。假设A表示微裂纹一端，则A端应力强度因子可由以下公式计算

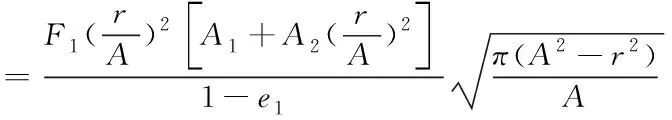
(4)

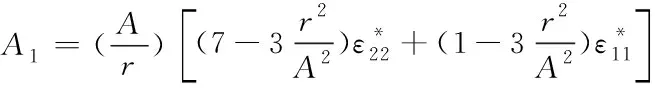
(5)

(6)

设l表示颗粒裂纹长度，延长颗粒半径r接近无穷大，则l=c-r，通过式(1)可知

(7)

上述公式为陶瓷合金材料垂直于截面半裂纹的应力强度因子，影响应力强度因子的原因很多，其中膨胀系数是其主要原因之一[8]，陶瓷表面垂直裂纹如图2表示。

图2 陶瓷表面垂直裂纹

2.2 热膨胀系数差对应力强度因子的影响

当温度相同时，釉面与陶瓷热应变情况不同[9]，二者热应变差值为颗粒本征应变，其计算公式如下

(8)

其中，釉面热膨胀系数由α1表示，陶瓷基体的热膨胀系数由α2表示，陶瓷整体的温度变化由ΔT表示。将式(8)所计算的数值代入到式(7)内，可计算陶瓷半裂纹上部受热膨胀在温度不同时的应力强度因子，其计算公式为

(9)

2.3 构建数值模型

选择陶瓷的任意一个表征单元体，将该单元体内的陶瓷表面微裂纹数量平均分配到该陶瓷材料参数内，设其为初始陶瓷裂纹单元，然后使用减弱或增强陶瓷参数方法可表达陶瓷表面微裂缝。受陶瓷材料内部空间点差异性的影响，依据蒙特卡罗方法，通过计算机随机函数生器生成陶瓷材料参数值，由于陶瓷材料力学参数大部分符合Weibull分布，因此构建符合Weibull分布的陶瓷表征单元体，其计算公式如下

(10)

其中，α1、u0分别表示热膨胀系数、与全部单元参数平均值相关的参数；Weibull分布密度函数形状由m定义，陶瓷材料的均匀度与参数m的大小成正比。

陶瓷材料的热传导和应力进行计算，热传导计算公式符合如下微分方程

λΔ2T+Q=ρcTt

(11)

T(P，t)|p∈Z1=φ(P，t)

(12)

(13)

T|t=t0=T(P，t0)

(14)

变形场、应力、边界条件等计算公式如下

σij，j+bi=0

(15)

εij=(ui，j+uj，i)/2

(16)

σij=λεijδij+2Gεij-βΔTδij

(17)

其中

(18)

(19)

β=(3λ+2G)α1

(20)

ΔT=T-T0

(21)

热传导的矩阵与陶瓷材料刚度矩阵受单元体材料参数影响各不相同，陶瓷材料的温度场与应力场受热传导矩阵和刚度矩阵影响而不同。

3 实验与分析

为实现在考虑釉面膨胀系数的条件下模拟陶瓷表面微裂纹的扩展过程，准备两组陶瓷试件，分别标记为试件A与试件B，两组试件模型如图3所示。

图3 试件模型

增加陶瓷试件顶部温度，初始温度设置为280℃，陶瓷试件左右及顶部放置于18℃的水中，两组陶瓷试件参数如表1所示。其中，试件A表面与试件B表面均有1条微裂纹，陶瓷试件A表面微裂纹尺寸为长3mm，宽1.5mm，陶瓷试件B表面微裂纹尺寸为长1mm，宽0.8mm。

表1 两组陶瓷试件参数

陶瓷材料在受热传导作用后，温度应力变化会较为明显。因此，为使实验数值更加准确，热膨胀系数取值分别为8、9、10，研究热膨胀系数对与陶瓷裂纹的影响，结果如图4所示。

图4 热膨胀系数对与陶瓷裂纹的影响曲线

综合分析图4结果可知，裂纹扩展长度与时间的增加成正比，且热膨胀系数越高陶瓷试件裂纹扩展长度越长。试件A与试件B在热膨胀系数分别为8和9时，试件的裂纹扩展长度增长较慢。当热膨胀系数为10时，试件的裂纹扩展长度增长迅速，其中试件A的裂纹扩展长度在膨胀系数相同时高于试件B的裂纹扩展长度。由此可知，不同膨胀系数对陶瓷试件裂纹扩展长度不同，热膨胀系数越高，裂纹扩展长度越大。

研究不同热膨胀系数下，陶瓷试件表面微裂纹的水平应力和时间的关系，结果如图5所示。

综合分析图5结果可知，x方向水平应力随着热膨胀系数的增加而增长，试件A的x方向水平应力增长缓慢但其数值高于试件B，试件B的x方向水平应力在时间为20s前增长迅速，时间超过20s后，试件B的x方向水平应力保持平稳状态，可见热膨胀系数越大，陶瓷试件x方向水平应力越大。

图5 不同热膨胀系数下陶瓷试件水平应力与时间关系

热传导系数也是导致陶瓷表面产生微裂纹的主要因素之一。为此，研究不同热传导系数对陶瓷裂纹长度影响，得到结果如图6所示。

图6 热传导系数对陶瓷裂纹的影响

分析图6可知，裂纹扩展长度与热传导系数成正比，热传导系数越高，裂纹扩展长度越大，其中，试件A裂纹扩展长度在为时间20s之前，不同热传导系数情况下，变化不大，时间超过20s之后，裂纹扩展长度逐渐增加。当时间超过40s后，随着时间的增加，裂纹扩展长度保持不变；试件B的裂纹扩展长度在热传导系数相同时要小于试件A。由此可知，利用本文方法可在不同情况下有效模拟陶瓷试件表面微裂纹扩展。

陶瓷表面微裂纹受应力强度因子作用，应力强度因子取值处于0.2～2.0之间。为此，对比不同应力强度因子对2组陶瓷试件表面微裂纹影响，得到结果如表2所示。

表2 不同应力强度因子对陶瓷试件微裂纹影响

综合分析表2可知，两组陶瓷试件表面微裂纹的长度与宽度都随着应力强度因子的增加而增加，当应力强度因子为0.8MPa之前时，两组陶瓷试件表面微裂纹的长度与宽度增长较缓慢，应力强度因子超过0.8MPa之后，两组陶瓷试件表面微裂纹的长度与宽度增长迅速。由此可见，应力强度因子数值越大，陶瓷试件表面微裂纹越大。

4 结束语

为研究釉面膨胀系数对陶瓷表面微裂纹扩展的影响，本研究设计了一种陶瓷表面微裂纹扩展模拟方法，并得到实验结果如下：

1)陶瓷试件表面微裂纹扩展长度与温度提升时间成正比，且膨胀系数越高，陶瓷试件裂纹扩展长度越长。当膨胀系数为10时，两组陶瓷试件表面微裂纹扩展迅速。

2)膨胀系数与陶瓷试件水平方向的应力成正比。膨胀系数越大，陶瓷试件方向水平应力越大。

3)热传导系数越高，陶瓷试件表面微裂纹扩展长度越大，两组陶瓷试件受自身参数影响，当热传导系数相同时，陶瓷试件B的表面微裂纹扩展长度小于陶瓷试件A。

4)应力强度因子为0.8MPa时，两组陶瓷试件表面微裂纹宽度与长度增加较缓慢，且随着应力强度因子数值增加，两组陶瓷试件表面微裂纹长度与宽度扩展越大。

本文研究虽然取得了一定成果，但由于陶瓷材料参数不同加工工艺不同，陶瓷材料的边界条件也不尽相同，因此，还需研究不同边界条件下陶瓷材料的热膨胀系数对陶瓷表面微裂纹的影响。陶瓷制品功能性不同，其形状不同，各个尺寸参数的热膨胀系数不同，因此无法在理论上计算其热膨胀系数，为适应陶瓷产业的飞速发展，需进一步对陶瓷热膨胀系数展开研究，为陶瓷产业提供更准确的技术支持。