基于改进ORB算法的单目视觉里程计研究

陆文超，杨慧斌，闫 娟，亢程博

(上海工程技术大学机械与汽车工程学院，上海 201620)

1 引言

自动引导小车(Automated Guided Vehicle，AGV)是组成现代生产物流的重要组成部分[1]。自主导航技术作为 AGV 核心技术之一，是 AGV 技术发展水平的最重要标志。视觉导航凭借能够在楼宇众多、城市信号阻塞等不利环境下实现自主导航，已成为时下SLAM自主定位的最优选择[2，3]。视觉里程计(VO)是SLAM至关重要的一环，通过相邻的两张图像来估计相机运动，连续的相机运动就规划出了AGV的运动轨迹，实现精确自主定位[4-6]。

单目视觉系统与深度相机定位系统、双目视觉系统相比，虽然定位精度较低但计算量较小，安装便捷[7]。VO作为视觉系统的输入，主要通过SIFT、SURF、ORB等特征点法提取特征因子。高云峰基于 Surf 算法的单目视觉里程计在一定程度上提高了定位精度，但存在实时性不足的问题[8]。王彭林研究的视觉里程计虽然具有实时性，但无法对定位过程进行优化，导致定位精度不高[9]。

视觉里程计是影响AGV整体运行的关键因素，针对以上相关研究成果存在的问题，提出基于改进ORB算法的单目视觉里程计技术研究方法，在保证ORB算法实时性的同时又增添SIFT算法的尺寸不变性，依据三种不同算法对特征点进行优化匹配，采用最小二乘法优化AGV位姿。通过实验验证，提出方法可以有效提高AGV定位精度，降低了AGV对高配置的依赖，增强视觉里程计的鲁棒性与实时性。

2 特征点的检测与匹配

2.1 ORB特征点

Rublee等人于2011年提出一种创新型检测与匹配特征点的方法—ORB算法[10]。ORB算法由关键点和描述子两部分构成。其中，ORB算法的关键点是基于原有的FAST角点进行改进而得到的“Oriented FAST”，描述子简称BRIEF。具体实现步骤为

1)ORB算法通过构建图像金字塔，在金字塔每一层中提取FASR特征点，解决尺度不变性的问题。

2)由灰度质心法实现特征的旋转。通过矩计算得出特征点的方向因子，图像的矩定义为

(1)

其中上式(1)中，p，q均代表矩的阶次，I(x，y)表示图像的灰度表达式。由上式得到图像的质心

(2)

由上式(2)得出的质心及与特征点的夹角即特征点的主方向

θ=arctan(m01/m10)

(3)

3)ORB算法使用改进的BRIEF算法对提取出的特征点计算描述子。ORB在FAST 特征点提取过程中，通过构建图像金字塔以及灰度质心法增添了尺度与旋转不变性，由此计算经旋转后的“Steer BRIEF”特征，所得到的ORB算法描述子的旋转不变性效果良好。

2.2 改进ORB特征算法

ORB 特征算法使用 FAST 提取特征点，在具备快速、高效等优点的同时也缺乏尺度与旋转不变性。考虑到AGV在行驶过程中，由于自身传感器的误差而导致的抖动以及不断根据需求调整前后运动，目标的尺寸将发生变化，因此所使用的算法需具备尺度不变性。SIFT是David G Lowe 在 1999 年提出的一种基于不变量描述子的匹配算法，对尺度平移、缩放、旋转、亮度变化等具有良好的不变性[11]，是目前较为成熟的特征点提取的算法。为有效解决此问题，本文提出将 SIFT算法所具有的尺度不变性特点和 ORB 算法快速、高效特点相结合，使用 SIFT 算法求出特征点和其质心尺度、方向后，用ORB算子描述特征点，并在特征匹配阶段利用均方根误差进行约束。因此，使得在保留了ORB算子运算快速度的优点的同时，解决ORB算法不具备尺度不变性的缺陷，将改进的 ORB算法自定义为 SIRB 算法。

2.2.1 SIRB 特征点提取

1)尺度空间极值检测

Lindeberg[12]等人已证明高斯卷积核是实现尺度变换的唯一变换核，并且是唯一的线性核。输入图像设为I(x，y)，G(x，y，σ)表示可变尺度的高斯函数，两者通过卷积得到图像的尺度空间：L(x，y，σ)，即

L(x，y，σ)=G(x，y，σ)*I(x，y)

(4)

使用差分高斯函数D(x，y，σ)如式(5)，高效得到

关键点的位置

D(x，y，σ)=G(x，y，kσ)-G(x，y，σ)*I(x，y)

=L(x，y，kσ)-L(x，y，σ)

(5)

上式D表示两个相邻的尺度差，初始图像与不同σ值的高斯函数卷积，将得到的一垛模糊图像临近两两相减得到对应的DOG。将DOG中的某个像素和本尺度的8个相邻像素以及上下相邻尺度各9个像素比较，如果该像素点在这所有参与比较的点中有最大值或者最小值，则认为该像素是尺度空间的极值点之一，极值检测原理如图1。

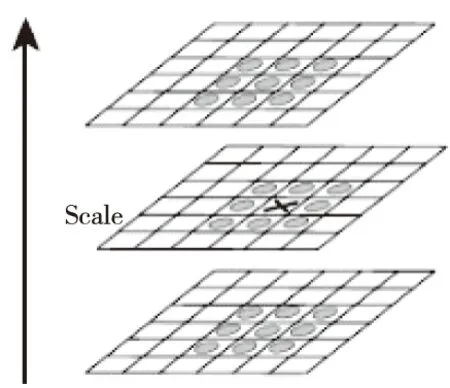
图1 极值检测原理图

2)精度特征关键点定位

为得到最终参与匹配的极值点，采用三维二次曲线展开的方法剔除对比度较低的边缘极值点。在像素点处用三维泰勒级数展开到2次方项，然后再精确定位极值的位置至亚像素级，展开式如下

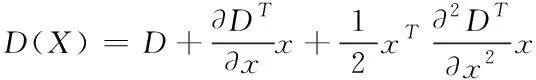
(6)

其中

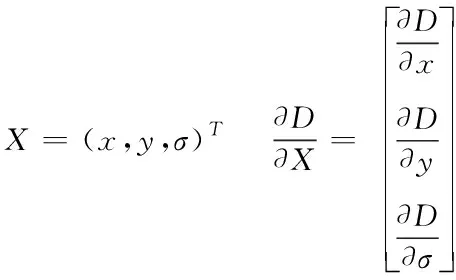
通过上式(6)求对x的偏导数，即可求得局部的极值，此时极值点对于展开点的偏移量x满足

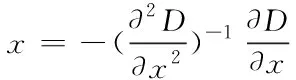
(7)

将式(7)带入式(6)，得

(8)

设定阈值为0.03，将|D(X)|<0.03的对比度偏低的点忽略，进而通过计算主曲率的比值去除不稳定的点，获取最终值。主曲率依据2×2的Hessian矩阵H来计算，其中：

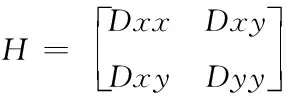
(9)

假定α和β是H的较大和较小特征值，则α=rβ，且

Tr(H)=Dxx+Dyy=α+β

(10)

Det(H)=DxxDyy-(Dxy)2=αβ

(11)

由式10与11得到：

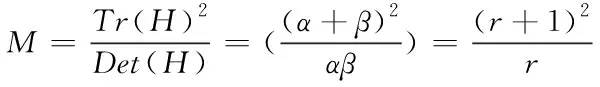
(12)

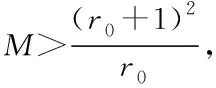
3)关键点主方向分配

关键点通过分配一个主方向，并将主方向纳入关键点的描述子特性之中，具有旋转不变性。描述主方向主要依据像素点的梯度。梯度的模和方向以像素差分的方法定义，如下所示

m(x，y)=(L(x+1，y)-L(x-1，y))2+

(L(x，y+1)-L(x，y-1))2

(13)

θ(x，y)=tan-1(L(x，y+1)-

L(x，y-1))/(L(x+1，y)-L(x-1，y))

(14)

关键点的主方向是通过统计以关键点为中心的一个邻域之内所有点梯度方向来确定。通过将梯度直方图分为36个柱形，每个柱形10度，关键点的主方向就是梯度方向峰值点的位置。

4)关键点描述子生成

依据上述得到带有位置、尺度，主方向的关键点信息，使用改进的Steer BRIEF算法快速对特征点计算描述子，保有快速的同时，所得到的特征子旋转、尺度不变性效果良好。

2.2.2 SIRB 特征点匹配

由于噪声等外界环境因素的影响，VO系统在图像特征点的匹配过程容易产生大量的误匹配点，影响相机定位。本文依据Brute-Force Matcher算法对相邻两个图像进行特征点的匹配，若满足Hamming dist < 2Min dist，则将两者视为正确匹配的特征点。在暴力匹配(Brute-Force Matcher，BF)算法的基础上，再采用快速近似最近邻( Fast Library for Ap-proximate Nearest Neighbors，FLANN)算法进行特征点匹配[13]。此方法在一定程度上减少了特征误匹配，同时视觉SLAM前端可估计相机采集相邻时刻图像的相对位姿。

为提高视觉SLAM前端特征点匹配的精确性，同时将机器学习的方法加入视觉前端[14，15]，提高图像匹配的鲁棒性、精确度、实时性是时下的发展趋势，但存在计算量较大的新难题。对此，文中Brute-Force Matcher算法FLANN算法基础上，提出在图像匹配过程中引入渐进采样一致性(Progressive Sampling Consensus，PROSAC)[16]。PROSAC 算法首先对所有特征匹配点的结果进行降序排序，不间断循环选取最佳结果进行迭代，消除了迭代次数不稳定问题，并得到最优解，提高了图像匹配精度。在二维平面通过选取随机点拟合直线过程中，先将聚集密集的点分为两个部分，然后设定距离阈值，选取最佳内点，最后拟合出最佳直线，PROSAC随机采样如图2。

图2 PROSAC随机采样图

PROSAC算法在图像匹配过程中可有效地剔除误匹配点，同时对每一对特征点建立欧式距离的比值β，比值越小，则说明距离越小，特征点匹配的质量也就越好。计算公式如下

(15)

式中，dmin表示最小欧式距离，dmin2代表次小欧式距离。

为验证基于ORB算法改进的SIRB算法对于特征点的提取，以及在结合Brute-Force Matcher算法与FLANN 算法的基础上，依据PROSAC算法在图像匹配过程中剔除误匹配点的有效性，运用Open CV等工具进行实验，实验证明此方法有效提高了特征点匹配的质量，特征点提取与匹配如图3、图4、图5、图6。

图3 SIRB特征点的选取

图4 Brute-Force Matche匹配

图5 Brute-Force Matche、FLANN匹配

图6 Brute-Force Matche、FLANN、 PROSAC匹配

上述实验中，用RMSE、RMSEx与RMSEy分别表示已知特征点坐标与检测出的特征点坐标间的整体均方根误差，X和Y向的均方根误差。提取的特征点间误差比较见表1。

表1 各算法提取特征点比较

三种算法提取的特征点花费的时间见表2。

表2 各算法检测特征点时间比较

为避免检测实验出现偶然性，采取多组实验进行验证，仿真结果表明，提出的SIRB算法相比SIFT算法和ORB算法具有较低的特征点提取误差，相比SIFT算法具有较高的特征点提取速度，并且相比ORB算法具有较高的特征点提取精度，保有快速提取同时，解决了ORB算子不具备尺度不变性的缺点。AGV对于不同路况的实时变化，不仅对尺度不变性有所要求，对实时性也提出较高要求。将改进的SIRB算法用于AGV特征点的特征提取上，在有效减少时间的基础上，还获得较高的鲁棒性。

3 位姿优化

由于噪音误差等带来的影响，非线性优化使用所有时刻采集到的数据进行状态估计，以此对相机位姿进行优化。经典的SLAM模型由运动方程和观测方程构成，如式(16)所示

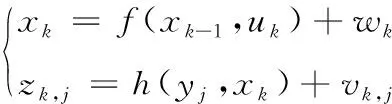
(16)

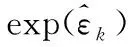
(17)

假设运动和观测方程的两个噪声项wk，vk，j均满足零均值的高斯分布：

wk～N(0，Rk)，vk～N(0，Qk，j)

(18)

通过引入最小二乘法求解上述构成的状态估计问题，所得到的观测数据的条件概率是：

P(zj，k|xk，yj)=N(h(yj，xk)，Qk，j)

(19)

如上式依旧满足高斯分布，使用最小化负对数求出其最大似然，得到使它最大化的xk，yj。假设任意高维高斯分布x～N(μ，ψ)，对其概率密度函数展开式取负对数，则得到

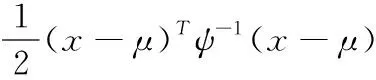
(20)

由于对原分布求解最大化相当于对上式负对数求最小化x，因此只需求解右侧的二次型项，将所得到对状态的最大似然估计带入观测模型，同时定义数据与估计值之间的误差

(ev，k=xk-f(xk-1，uk)

(21)

ey，j，k=zk，j-h(xk，yj)

(22)

求得该误差的平方和

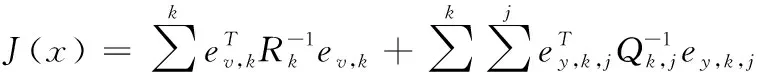
(23)

对得到的最小二乘方程进行求解，得到导数为零的极值，它们可能是极大、极小或鞍点处的值，然后逐个比较它们的函数值大小即可。对于难求解的最小二乘问题，采用迭代的方式，即从一个初始值出发，不断地更新当前的优化变量，使目标函数下降。这个过程只要找到迭代点的梯度方向即可，进而通过如下改良的非线性优化列文伯格—马夸尔特方法不断迭代优化求解。

1)给定初始值与初始优化半径x0、μ；

2)求解第w次迭代

(24)

其中μ是信赖区域的半径，列文伯格把D取成单位阵I，马夸尔特提出将D取成非负数对角阵，ρ的计算如式(25)所示

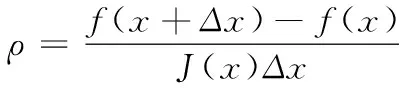
(25)

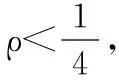
5)如果ρ大于某阈值，则认为可行，令xk+1=xk+Δxk；

6)判断算法是否收敛，若不收敛则返回2)，若收敛则结束。

4 实验结果与分析

本文实验采用内置机载 PC(i7 处理器、1.8GHz CPU 、睿频 3.0GHZ)的小强XQ5轮式机器人。小强XQ5配置60fps 178度广角摄像头广角单目摄像头，在 Ubuntu 系统中依据机器人操作系统 ROS，以及解决图像处理的 Open CV 库和用于实现优化算法的 g2o 库，以此实现小强XQ5能够自主定位，小强XQ5如图7。

图7 小强XQ5实物图

在室内实验室对本文设计的单目视觉里程计进行实验。小强XQ5匀速在室内无规则行驶，不间断检测周围环境且提取室内图像中的特征点，在相同配置的硬件下，特征提取及匹配时间短，有效提高了实时性。小强XQ5标准轨迹与视觉轨迹对比如图8，标准轨迹里程约16.70m，视觉轨迹里程约为16. 86m，最大误差约为0.16m，误差为0. 95% ，两者轨迹基本拟合。SIRB算法整体的误差较ORB检测方法减小0.04m，定位精度提高0. 24%，相比较SIFT检测方法误差减小0.03m，提高0. 18%的定位精度。SIRB算法可最大化减小误差，有效提高定位精度，效果更佳。SIRB算法、ORB算法以及SIFT算法的定位误差对比如图9。

图8 小强XQ5标准轨迹与视觉轨迹对比图

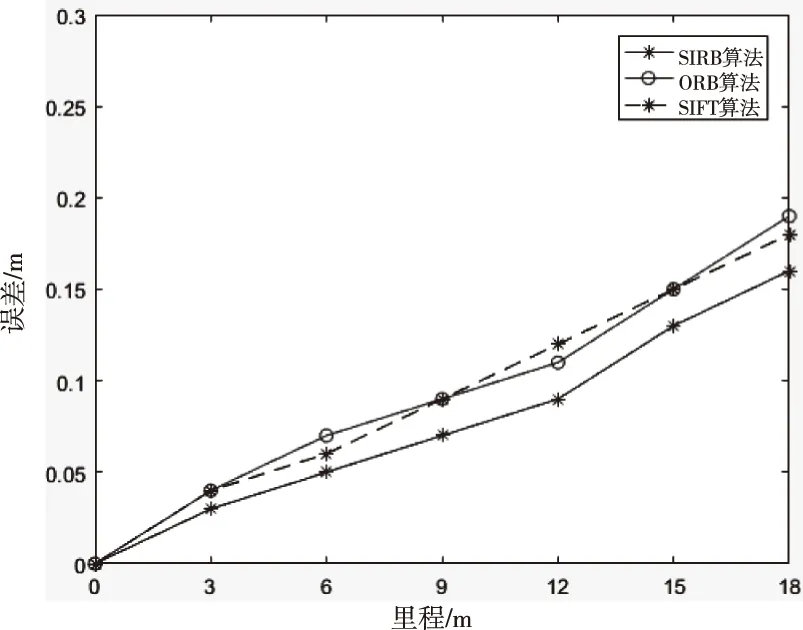
图9 定位误差对比图

5 总结

本文提出的基于改进ORB算法的单目视觉里程计方法：

1)采用SIRB算法对特征点进行快速高效的提取。

2)结合暴力匹配算法与FLANN 算法以及PROSAC算法进行快速匹配并剔除误匹配，快速高效估计机器人位姿状态。

3)构建最小二乘问题，利用改良的列文伯格—马夸尔特方法以及非线性优化库g2o 对AGV位姿进行优化。

以小强XQ5为实验载体验证得出，本文方法能有效增强视觉里程计的鲁棒性，提高AGV定位精度。