改进的引力搜索算法及在波束赋形中的应用

孙翠珍

(西安科技大学通信与信息工程学院，陕西 西安 710054)

1 引言

阵列天线波束赋形属于阵列综合问题，是通过确定阵列天线的激励幅度、相位，阵元个数等参数，使辐射方向图尽可能接近要求的天线阵辐射特性的过程。阵列赋形可以很大程度地简化天线设计的复杂度，并且降低设计成本，因此成为天线设计过程中的热点研究问题[1]。波束赋形大多数都具有非线性、不可微、多参数的特点，利用解析方法及数值优化方法很难得到期望的辐射方向图。启发式算法由于具有鲁棒性强、适应范围广、计算能力强且对优化目标没有过多约束等特点，因此成为波束赋形领域的有效计算工具。该类算法中的传统算法如遗传算法(Genetic algorithm，GA)[2]、粒子群优化(Particle swarm optimization，PSO)[3]已被用于阵列赋形问题中并取得了满足设计要求的结果。2009年，Esmat Reshedi等人提出了引力搜索算法(Gravitational search algorithm， GSA)[4，5]，该算法作为一种启发式算法，具有高效的优化性能，已经在天线设计领域得到了广泛的应用[6-9]，但是对于复杂的阵列赋形问题，该算法在优化过程中的优化精度低且收敛速度慢。

论文中提出了一种改进算法：伪反向学习引力搜索算法(Quasi-oppositional gravitational search algorithm， QOGSA)。首先，为提高GSA的收敛速度，设计了一种新的反向概率probq，它随着迭代次数的变化而变化，将其用于伪反向学习机制(Quasi opposition-based learning， QOBL)[10]中，替换掉QOBL中的固定反向概率，优化了QOBL用于GSA中的时机；其次，为提高算法的优化精度，定义了“精英粒子”，并用其替换掉下一代种群中适应度值较差的粒子，改善了种群的多样性。将基于可调反向概率probq的QOBL以及精英粒子嵌入GSA中，提出了QOGSA，基于不同的仿真实例表明，QOGSA在优化精度、收敛速度方面均优于GSA算法，更适合于解决复杂的阵列天线波束赋形问题。

2 引力搜索算法及方向图

2.1 引力搜索算法实现过程

引力搜索算法是一种基于万有引力定律搜索机制的智能优化算法，种群中粒子的位置对应于问题的解[5]。粒子的质量大小与适应度值成正相关，粒子所在位置越优，其质量越大。根据万有引力和牛顿第二定律，粒子之间相互吸引且都向质量最大的粒子靠近，即所有解都逐渐向最优解靠近。经过一定次数的迭代，所有的粒子将会聚集在最优个体周围。种群中最大质量的粒子所在位置即为问题的最优解。

步骤1：初始化群体中各粒子的位置、速度；

(1)

(2)

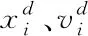
步骤2：计算种群中粒子的适应度值和质量；

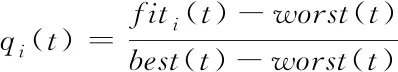
(3)

(4)

其中fiti(t)表示第t次迭代时粒子i的适应度值；best(t)和worst(t)表示第t次迭代时种群的最优适应度值和最差适应度值；Mi(t)为第t次迭代时粒子i的质量。

步骤3：计算每个粒子在各个维度受到引力的合力；

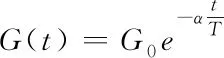
(5)

(6)

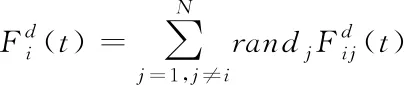
(7)

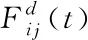
步骤4：计算粒子的加速度和速度；

(8)

(9)

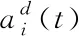
步骤5：更新粒子所在位置；

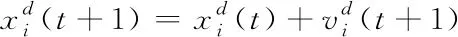
(10)

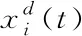
步骤6：如果满足终止条件，则输出最优粒子位置，并终止算法；否则转向步骤2。

2.2 方向图及适应度函数

N元等间距线阵的归一化方向性函数如下

(11)

其中In是阵元n的复激励(激励幅度和相位)；Fmax是方向性函数最大值，θ为阵列轴线与射线方向之间的夹角，N为阵元数目，k为波数，d为阵元间距。

阵列天线中，适应度函数的设置和方向图的误差相关，而优化过程中要综合考虑方向图的主瓣和旁瓣误差，同时为了避免误差出现0值影响后续计算，论文中把最小值问题转化为最大值问题进行处理。适应度函数设置如下

f=100/(1+α·ffit1+β·ffit2+γ·ffit3)

(12)

其中ffit1=(FNBW-FNBWde)2，FNBW，FNBWde是实际方向图的零功率主瓣宽度和期望方向图的相应值；ffit2=(MSL-MSLde)2，ffit3=(MML-MMLde)2。MSL，MSLde是最大旁瓣电平及其期望值；MML，MMLde代表了主瓣最大抖动及其期望值。α，β，γ为权值系数。

3 伪反向学习引力搜索算法实现过程

3.1 概率可调的伪反向学习机制

论文中对QOBL[10]中的固定反向概率进行了改进，设计了一种可调反向概率probq。

在QOBL实现过程中，计算每次反向操作后，反向操作值优于原始值的个体数量Ns及其概率Ps，将迭代次数按照反向学习周期划分，经过一个反向周期PNmax次迭代后，统计Ps的平均值Psav，最大值Psmax及最小值Psmin。Pst代表第t次迭代后的Ps。

(13)

根据Ps的变化趋势动态调整probq的大小

probq=probq*ZF

(14)

当

(15)

否则

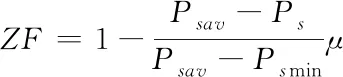
(16)

其中，μ是控制因子，PNmax是反向周期，在利用算法进行优化的过程中，这两个参数的取值要兼顾收敛速度和计算精度，经过反复试验，论文中μ设置为4，PNmax取为5。

当反向操作可以产生更多的优秀个体时，说明此时的种群需要更多的反向操作，按照调整过的probq就可以在后续迭代过程中增加反向操作的机会；反之亦然。这样可以根据实际需求，来自适应调整反向操作的次数，优化反向时机，从而提高全局收敛速度。

3.2 精英粒子

(17)

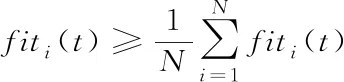
(18)

满足上面两个表达式的粒子为精英粒子。精英粒子虽然与最优粒子的距离较大，在迭代过程中很可能被淘汰，但是由于其适应度值好于平均值，周围存在最优解的概率较大，若用其替换掉下一代种群中的较差个体，可以提高种群的多样性，从而提高算法的优化精度。

3.3 伪反向学习引力搜索算法实现步骤

将基于可调概率的QOBL和精英粒子嵌入GSA，形成了QOGSA，其实现步骤如下：

步骤1：初始化种群P0，粒子个数为Np个；

步骤2：利用QOBL产生P0的伪反向学习种群QOP0；

步骤3：重新产生种群；根据式(12)计算P0、QOP0中粒子的适应度值，从中挑选Np个最优个体作为初始种群P0；

步骤4：probq的计算；每隔PNmax次迭代，计算Ps，Psmax，Psmin，根据式(13)计算Psav，根据式(15)(16)判断计算ZF，式(14)计算可调概率probq；

步骤5：精英粒子的选择；根据式 (17)-(18) 计算精英粒子。并用最优粒子及精英粒子替换下一次迭代时适应度值最差及次差的粒子；

步骤6：GSA中各变量的计算；根据式(3)-式(10)计算相应值；

步骤7：迭代过程中进行QOBL；判断probq，若其在规定的范围内(小于0.3)[10]，对当前种群进行QOBL操作，并进行步骤3；

步骤 8：判断是否终止；若满足终止条件，停止迭代；否则重复步骤2-步骤7。

4 算法的验证及结果分析

利用QOGSA实现多个目标的波束赋形，并且和GSA进行对比，为客观准确地比较算法的性能，GSA和QOGSA的参数取值均参照文献4，包括种群个数取50，G0=100，α=20。

4.1 阶梯包络波束赋形

设计一个26元阶梯包络阵列，其方向图的具体要求为：主瓣宽度10°，式(12)中，旁瓣区域θ∈[-40°，-5°]∪[5°，40°]对应的MSLde=-30dB，θ∈[-90°，-40°]∪[40°，90°]的MSLde=-40dB；d=λ/2，α=0.45，β=0.55，γ=0。对阵元激励进行优化，GSA[4]和QOGSA的迭代次数相同，均为1000次。

图1是两种算法综合得到的方向图曲线，QOGSA的方向图两个旁瓣区域的电平均低于GSA；图2是适应度值曲线(收敛曲线)对比，当迭代次数超过300次时，QOGSA和GSA的适应度值趋于稳定，且前者的稳定值要高于后者，说明经过1000次迭代，QOGSA得到的方向图更接近期望方向图，优化精度更高。当适应度值相同，即主瓣和旁瓣的误差和相同时，QOGSA需要的迭代次数略少，说明该算法收敛速度略快于GSA。表1是两种算法具体的优化结果对比，在主瓣展宽程度相同的情况下，论文中提出的 QOGSA算法优化得到的峰值旁瓣电平分别为-30.5126dB和-40.5669dB，与GSA算法相比(-29.5991dB和-39.6370dB)，分别降低了0.9135dB和0.9299dB。综上，QOGSA在收敛速度略快于GSA的基础上，优化精度得到了大幅度提高，进一步验证了QOGSA的优化性能。

表1 基于GSA算法和QOGSA算法的优化结果对比

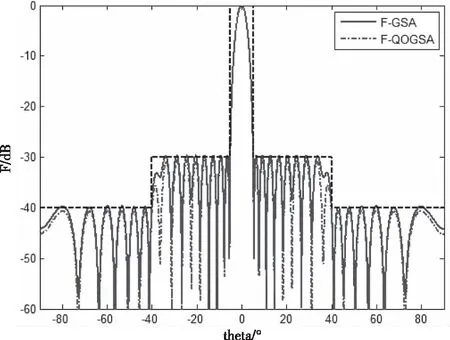
图1 两种算法优化的方向图比较

图2 两种算法的收敛曲线比较

4.2 余割平方波束赋形

设计一个20元直线阵列，要求其主瓣为余割平方包络，方向图的具体要求为：零功率主瓣介于[85°，130°]之间，式(12)中，主瓣抖动MMLde在±0.5dB之间， MSLde=-20dB，d=λ/2，误差系数α=0.4，β=0.2，γ=0.4。本节除了将QOGSA和GSA[4]进行比较，还和文献中的GA[2]、PSO[3]算法的性能进行了比较，4种算法迭代次数均为1000次。

仿真得到的方向图曲线如图3，QOGSA优化得到的方向图无论是主瓣还是旁瓣均为最优，GSA算法次之；图4是在相同迭代次数的条件下，4种算法的适应度函数曲线(收敛曲线)对比，QOGSA和GSA经过相同迭代次数，可以得到比GA和PSO更好的适应度值，QOGSA的优化精度在4种算法中最佳。迭代超过400次时，QOGSA的优势更明显，此时其收敛速度快于GSA，并且当适应度值要求超过90时，GA和PSO增加迭代次数，其适应度值也不能满足要求，说明QOGSA和GSA可以改善GA和PSO算法局部最优的问题。表2是4种算法的设计指标及具体优化结果对比，可以看出，GSA和QOGSA综合得到的峰值旁瓣电平(-19.7236 dB和-20.7584dB)明显要低于GA和PSO算法(-18.7719 dB和-18.2530 dB)； QOGSA在主瓣抖动最小(0.7398dB)的情况下，其旁瓣区的峰值电平最低(-20.7584 dB)，且零功率主瓣展宽远小于其它3种算法(1.8°)。QOGSA以快于GSA，GA，PSO三种算法的收敛速度得到了最优解。

图3 四种算法优化的方向图比较

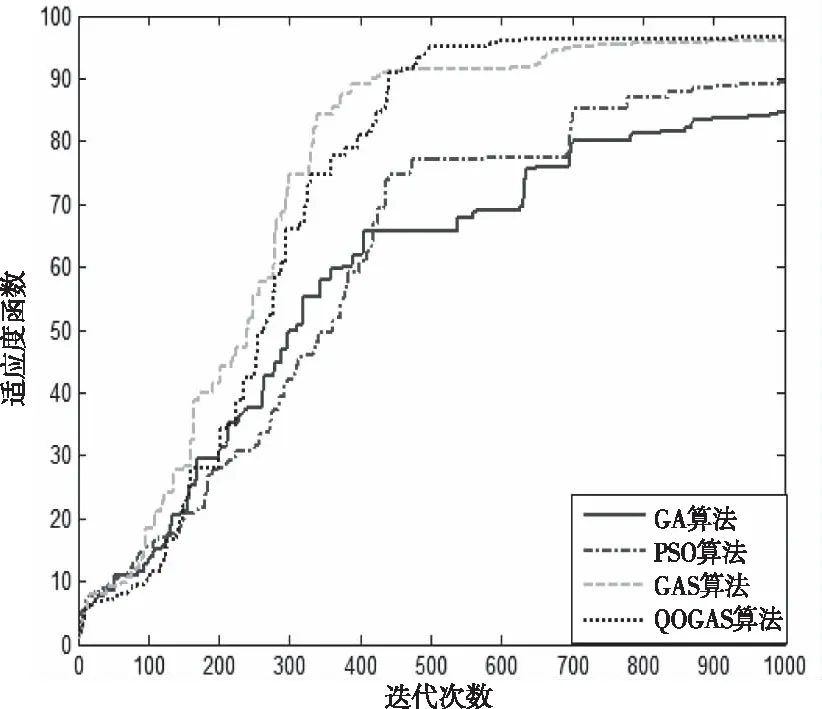
图4 四种算法优化的收敛曲线比较

表2 四种算法优化余割波束的结果对比

5 结论

为了解决GSA用于复杂的波束赋形时优化效果不理想的问题，提出了一种改进算法：基于概率可调伪反向学习机制的引力搜索算法(QOGSA)。首先针对QOBL中反向概率固定带来的反向时机判断不准确的缺点，设计了一种随迭代次数变化而动态调整的概率probq，将其用于QOBL和GSA中，可以调节种群全局探索能力和局部开采能力的平衡，提高算法的收敛速度；其次为提高种群的多样性，定义了精英粒子，在GSA迭代过程中保留该类粒子，并用其替换下次迭代时的次差粒子，从而大大改善了算法的优化精度。通过对阶梯包络波束、余割平方波束的优化结果可以看出，和同类算法GSA、GA、PSO相比，在迭代次数以及算法控制参数相同的条件下，QOGSA在收敛速度得到提高的基础上，主瓣展宽小，旁瓣电平低，主瓣抖动小，更适合应用于复杂的阵列波束赋形问题。