基于能量最优的多约束小卫星碰撞规避控制
洪 涛,王国刚,杜 斌
(1. 中国西安卫星测控中心,陕西 西安 710000;2. 长光卫星技术有限公司, 吉林 长春 130000)
1 引言
随着时代的发展,空间任务的复杂性越来越高,单凭一颗或者几颗大卫星已不能满足某些领域的任务要求,因此采用小卫星星座来完成单星完成不了的任务,小卫星星座包含少则几十颗多则上百颗卫星,卫星的数量之多,增加了卫星间的碰撞风险系数,碰撞预测和规避控制是防止小卫星碰撞的有效且可行的手段[1-2]。若忽视碰撞安全问题,可能会导致卫星碰撞而造成灾难性后果。
由于卫星长期在轨运行空间碎片环境中,以及任何的外部摄入和内部故障都会引发卫星发生碰撞[3],从而导致任务失败,所以要对星座构形控制过程中的碰撞预测和碰撞规避进行研究。目前碰撞预测的研究方法非常多,如区域法碰撞预警[4]、差分GPS载波相位碰撞检测[5]、位置协方差计算碰撞概率[6]、卫星碰撞预报并行算法[7]等,但是规避碰撞措施的研究比较少。文献[8]提出了基于粒子群优化(PSO)算法的在线轨迹优化算法, 并将其应用于卫星编队保持控制系统之中, 实现了高精度、低能耗的快速稳定控制,避免了编队卫星间的碰撞。文献[9]采用有界概率椭球理论计算碰撞概率,提出一种自主在线碰撞规避方法。针对小卫星星座来说,存在应用约束和携带燃料的约束,考虑在原有的构形基础上进行碰撞规避控制非常有必要。
以上的碰撞规避控制研究中,未考虑实际的工程应用约束,本文考虑了载荷约束、测控资源约束、星座构形约束等,采用数学表征法建立各约束的数学模型,针对带有约束的轨道动力学模型,设计了一种能量最优的碰撞规避控制算法。结合实际的工程应用需求和现有的地面站资源条件以及在轨卫星的构形约束,采用最优霍曼理论,实现多约束下的能量最优碰撞规避。
2 轨道动力学建模
2.1 轨道建模
两颗卫星d和g正常在轨飞行,当t时刻,卫星d与卫星g相交于空间某一点,两颗卫星即发生碰撞。设卫星d当前的位置和速度为r1和v1,卫星g当前的位置和速度为r2和v2,则卫星碰撞图如图1所示。

图1 卫星碰撞示意图

ρ=r1-r2
(1)
当|ρ|≤ρm时,ρm为两颗卫星间允许的距离,需要提前将规避星施加某一个方向的推力,使规避星避开目标星,防止两颗卫星碰撞。假设两个航天器都受到与距离平方成反比的中心引力作用,且目标航天器不施加主动轨道控制,则有

(2)
其中,aT为规避航天器的推力加速度。
2.2 约束建模
2.2.1 有效载荷约束
遥感卫星的载荷与高度密切相关,当轨道高度越高,载荷的分辨率将会下降,不满足用户需求;当轨道高度越低,卫星的轨道衰减越快,使用寿命大大减少。
成像载荷设计的分辨率为fl,分辨率允许偏差值为fp,可运行在轨道高度为H,则卫星轨道允许的高度为

(3)
轨道高度偏差就是载荷对轨道高度的约束,轨道半长轴满足
H+ae≤Hp+ae
(4)
2.2.2 测控资源约束
首先确定可利用的测控站,尽量选择在测控弧段内进行轨道规避调整,当可以预测到碰撞位置和时刻后,选择可利用的测控站进行控制指令发送,执行规避控制。

(5)
碰撞时刻为t,则控制约束为
t-T>TL
(6)
其中,TL为规避控制提前时间,TL>4Tz,Tz为规避星的轨道周期,当最接近TL的测控站资源被占用,调用次接近TL的测控站资源,依次递推,得出适合的测控站资源。
2.2.3 控制策略约束
遥感小卫星质量轻,携带的燃料少,因此采用能量最优规避控制。当跟踪星进入目标星的安全范围后,给出跟踪星控制标志,制定控制策略,将碰撞点作为轨道转移的远地点,控制点火时刻选择在转移轨道的近地点时刻,选择合适的测控站上注指令,最优控制量指标为
Δr=az-ag
(7)
其中,az为以碰撞点为转移轨道的远地点的轨道半长轴,ag为规避星的轨道半长轴。
2.2.4 星座能力约束
对于商业遥感星座,重访和覆盖是客户最为关心的能力,相位分布情况直接影响重访能力,因此,相位分布的保持尤为重要,若同一个轨道面上的卫星高度相差较大,几天时间就会超出允许相位差,因此控后尽量回到原来的高度或百米级的高度差。
假设速度增量为u,卫星角速度为n,则半长轴变化量Δa为

(8)
卫星轨道周期为T,轨道控制后周期为Th,则每天的相位漂移速度为

(9)
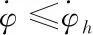
(10)
3 碰撞规避控制设计
3.1 控制策略
对于碰撞规避,通过改变相对半长轴来实现星间的安全飞行。假设两颗卫星,一颗为在轨正常运行的目标卫星,另一颗变轨卫星不断靠近目标星,采用主动控制策略,假设变轨星从A点到B点的轨迹路径的任意一点到目标星的距离为r(t),目标星的安全球半径为rs,则定义
Δr(t)=r(t)-rs
(11)
其中,Δr(t)为变轨星在路径上与安全球的距离。其最小值Δr(t)min可以作为用来判断是否发生碰撞的准则。判断准则为:

(12)
当Δr(t)min>0时,变轨星与目标星不会发生碰撞的风险;当Δr(t)min=0时,变轨星与目标星存在碰撞的风险;当Δr(t)min<0时,变轨星与目标星会发生碰撞的风险。rs=rs1+rΔ,其中rΔ为预留距离,即准备启控时间。
3.2 多约束下最优控制策略
设有以地心为中心的圆轨道1和椭圆轨道2,半径分别为r1和r2,设r2>r1,航天器在轨道1上的K点施加与当地速度vc1同方向的速度增量Δv1,进入椭圆转移轨道2,椭圆轨道H点为远地点,具体见图2。
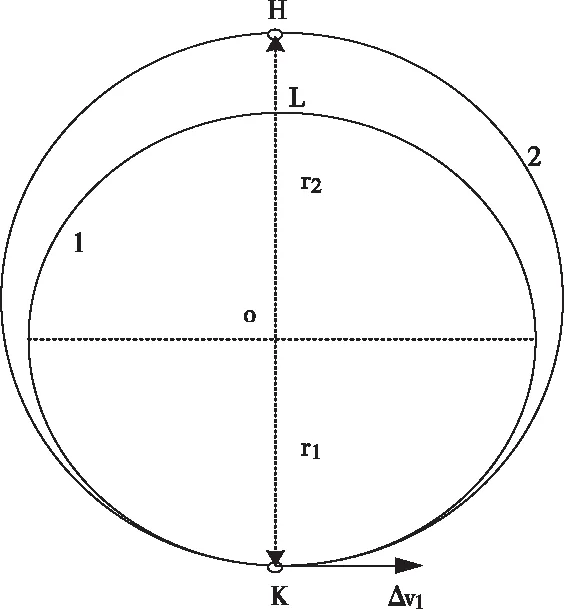
图2 轨道转移过程图
根据轨道的能量公式可知,轨道1的机械能为
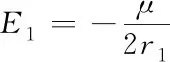
(13)
由轨道1到轨道2需要增加轨道能量,假设在K点的速度增量Δv1不是沿着vc1的方向,而是与vc1存在夹角θ,如图3所示。

图3 速度增量施加方向的影响
则在K点的机械能的变化为

(14)
由上式可知,要想增加机械能ΔE,当θ=0时,Δv1最小,相当于最省能量。此时所有的能量都用来增加轨道的动能,不存在仅改变速度方向的分量Δv12。由此可定性的理解霍曼转移的最优性。
θ=0意味着K点和H点为转移轨道的近地点和远地点,将两颗卫星的碰撞点选择在L点,点火点选择在近地点K点,这样一来,两颗即将碰撞的卫星在远地点L处的距离最大。假设两颗卫星间的安全距离为r2-r1,在轨道面内调整轨道来规避卫星间的碰撞,在加入机械能ΔE时,两颗卫星在H点处达到最大距离。
椭圆转移轨道的半长轴ra=(r1+r2)/2,因此轨道的能量为

(15)
在K点,航天器由初始轨道进入转移轨道,需要的能量增量为

(16)
在K点处,机械能的改变都是动能的改变,因此有

(17)
记nT=r2/r1,由式(1)和(2)可得
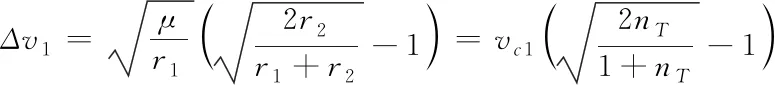
(18)
因此,霍曼转移的特征速度为

(19)
霍曼转移的时间为椭圆轨道周期的一半,即
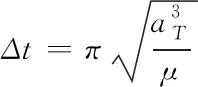
(20)
霍曼转移是共面圆轨道间、时间自由的冲量全局最优转移。实际控制中,将远地点作为碰撞位置,在近地点进行点火,即燃料最省,也可以有效地规避碰撞。
4 算例分析
4.1 仿真输入
1)选择二体递推模型进行递推;
2)轨道初始值和控制策略参数如表1和表2;

表1 卫星初始轨道参数

表2 控制策略参数
3)最小安全距离设置为300m,小于300m时即发出预警,并进行碰撞规避。
根据有效载荷,星座构性约束、测控资源约束等数学模型,可知,
当有效载荷分辨率为1m(@500km),允许分辨率上限为1.002m,则允许调整的轨道高度不高于501km;
当规避星轨道有两颗卫星,以180°等相位分布,允许相位偏置7°,当调整50m时,相位差飘出0.059°/天,则118天飘出应用需求允许范围,因此允许调整的轨道高度范围±50m以内,要求比较苛刻,因此,第一次在转移轨道近地点处,卫星飞行方向施加速度增量,第二次仍在近地点处,卫星飞行反方向施加相同的速度增量,使规避卫星回到原来轨道;
可用的测控站位长春站、三亚站和喀什站,启控时刻尽量选择在可利用的较近的测控弧段内,可选择境外启控。
4.2 数值仿真
采用Mmatlab进行数值仿真,仿真时间24小时,设置目标星安全距离为300m,两颗卫星2018.7.11 03:59:45开始发生碰撞,则燃料最优规避控制策略仿真如下。
选择有效载荷约束,星座构性约束、考虑测控资源约束,进行燃料最优规避控制。假设载荷允许卫星轨道的最大高度调整范围为200m以内;星座构形约束卫星轨道最大高度调整范围50m以内;选择合适的测控站为长春站,上注延时控制指令,选择转移轨道的近地点时刻为点火时刻,点火方向和控制量见图4所示。

图4 燃料最优控制
从图4可知,规避星在转移轨道的近地点处沿着飞行方向进行点火控制,转换到惯性系下的三轴的速度增量为X轴:0.0002m/s2,Y轴:0.0001m/s2,Z轴:0.0018m/s2。将碰撞点选择为远地点,在载荷约束的情况下,则在碰撞点处两颗星的距离最大达到300m,超出了碰撞距离,控制前后的半长轴差在转移轨道的远地点处为200m,误差在2m以内,惯性系下的卫星轨道如图5-7所示。

图5 惯性系下卫星轨道
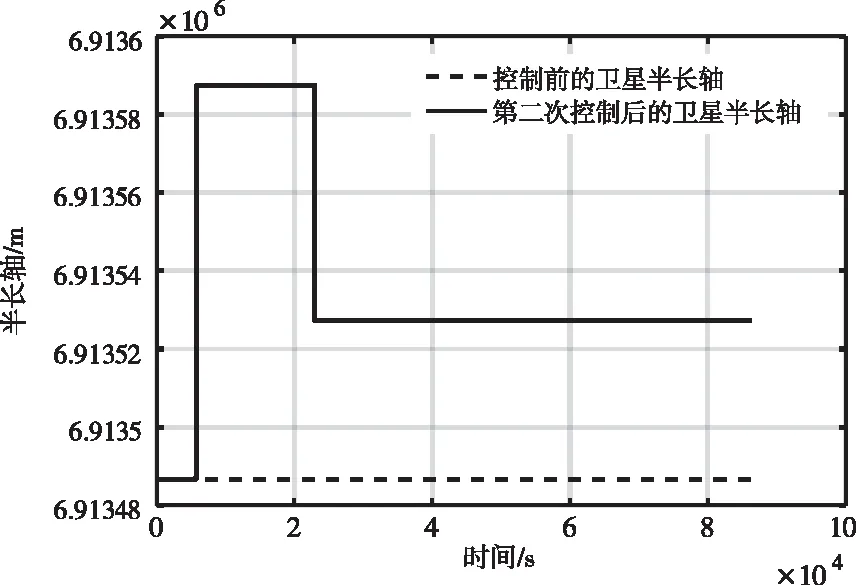
图6 规避星控前控后轨道半长轴
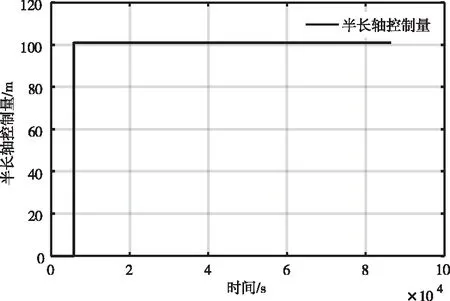
图7 第二次轨道半长轴控制量
由图5-7可知,当两颗卫星距离小于300m时,卫星将要碰撞,至少提前2.5个轨道周期在长春站内上注指令,在近地点处开始进行轨道碰撞控制,在远地点时两颗星的距离达到200m,再回到近地点时第两次点火,半长轴控制量不超过100.8m,第二次控后的轨道半长轴为6913.527km,控前轨道半长轴为6913.487km,控制前和控制后轨道半长轴差为40m,在星座构形约束范围内,满足控制约束要求,两颗卫星碰撞规避如图8所示。

图8 碰撞规避图
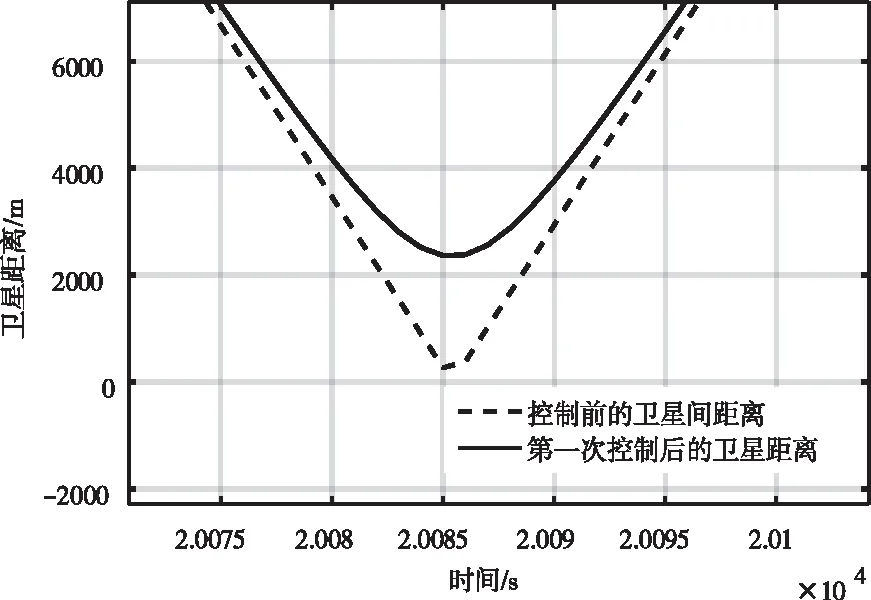
图9 碰撞规避局部放大图
从图8和9可知,当2018.7.11 03:59:45时,两颗卫星的距离小于300m,碰撞规避控制后的两颗卫星最小距离为2300m,在星座构形约束和载荷约束的条件下,完成规避控制,半长轴变化40m,因此以最优燃料控制规避了两星碰撞。
仿真效果可知,在存在约束和不存在约束的情况下,采用设计的自主碰撞规避算法很好的实现了卫星的自主碰撞规避,证明了最优碰撞规避算法的有效可行。
5 结论
本文设计了一种多约束下的能量最优的碰撞规避控制解决了小卫星间近距离碰撞问题。
1)采用轨道力学和数学表征法建立了惯性系下的小卫星轨道动力学模型和约束模型;
2)根据带有约束的动力学模型,制定了碰撞规避策略;
3)通过数值分析了给出最优的控制方向和控制时刻,采用霍曼变轨理论给出了最优条件下的速度增量,实现了卫星间的碰撞规避。
最后通过数学仿真给出有约束的碰撞规避轨迹,证明了设计的控制算法的有效性和可行性。

