单轴转向架跨座式单轨车辆悬挂系统参数优化分析

文孝霞，韩轲，杜子学

(重庆交通大学 轨道交通研究院，重庆 400074)

目前，跨座式单轨车辆有两种典型结构型式的转向架，即单轴式转向架和双轴式转向架，它们在转向架构造、道岔、轨道梁等方面具有较大的区别[1]，从而导致运行机理和动力学性能等方面存在明显差异.单轴转向架跨座式单轨车辆(简称单轴式单轨车辆)的转向架是只有一个轮对的非传统转向架[2]，具有质量轻、线路适应能力强、牵引能耗低、结构简单、制造成本低等优点，使单轴式单轨车辆特别适用于中、小运量需求的城市轨道交通支线、辅助线和旅游线路.为了适应中、小城市轨道小运量的运输需求，轨道企业积极开发新型单轴式单轨车辆产品，抢占中、小运量轨道运输的市场份额.单轴式单轨车辆具有复杂的空间杆系结构，由于悬挂系统和复杂空间杆系结构之间的相互作用对车辆过弯时的导向性能产生影响，导致车辆的曲线通过性能变差、走行轮磨损严重等问题.因此，对单轴式单轨车辆过弯时的导向性能及走行轮磨损的减少等方面进行研究具有重要的意义.

目前，国内外在跨座式单轨车辆领域的研究主要集中于车辆系统动力学及车轨耦合动力学方面.Jiang等[3]对车辆系统动力学进行研究，建立铰接式跨座式单轨车辆动力学模型，通过车体加速度响应与现场试验结果的比较，验证单轨车辆模型的有效性.任利惠等[4]考虑轮胎的径向刚度、侧偏刚度及走行轮的纵向滑转等因素，建立跨座式单轨车辆曲线段动力学分析模型，发现水平轮预压力的大小对跨座式单轨车辆的曲线通过性能具有显著的影响.杜子学等[5]基于多刚体动力学理论，建立跨座式单轨车辆动力学仿真模型，仿真结果表明，曲线超高率和半径对跨座式单轨车辆曲线通过性能有较大的影响.梁志华[6]结合地铁车辆的曲线通过性能评价指标，制定跨座式单轨车辆曲线通过性能评价指标.基于此，本文对单轴转向架跨座式单轨车辆悬挂系统参数优化进行分析.

1 单轴式单轨车辆动力学模型

1.1 车辆走行机理分析

单轴式转向架，如图1所示.新开发的单轴式单轨车辆的转向架只有一个单独的轮对，结构形式不稳定，为了保持转向架和车体之间的相对平稳，防止转向架出现俯仰和摆振等现象，需要在车体和转向架构架之间设置约束装置，即空间杆系结构.空间杆系结构主要由牵引组件、抗点头扭杆等组成，抗点头扭杆一端与车体相连，另一端与转向架构架相连.

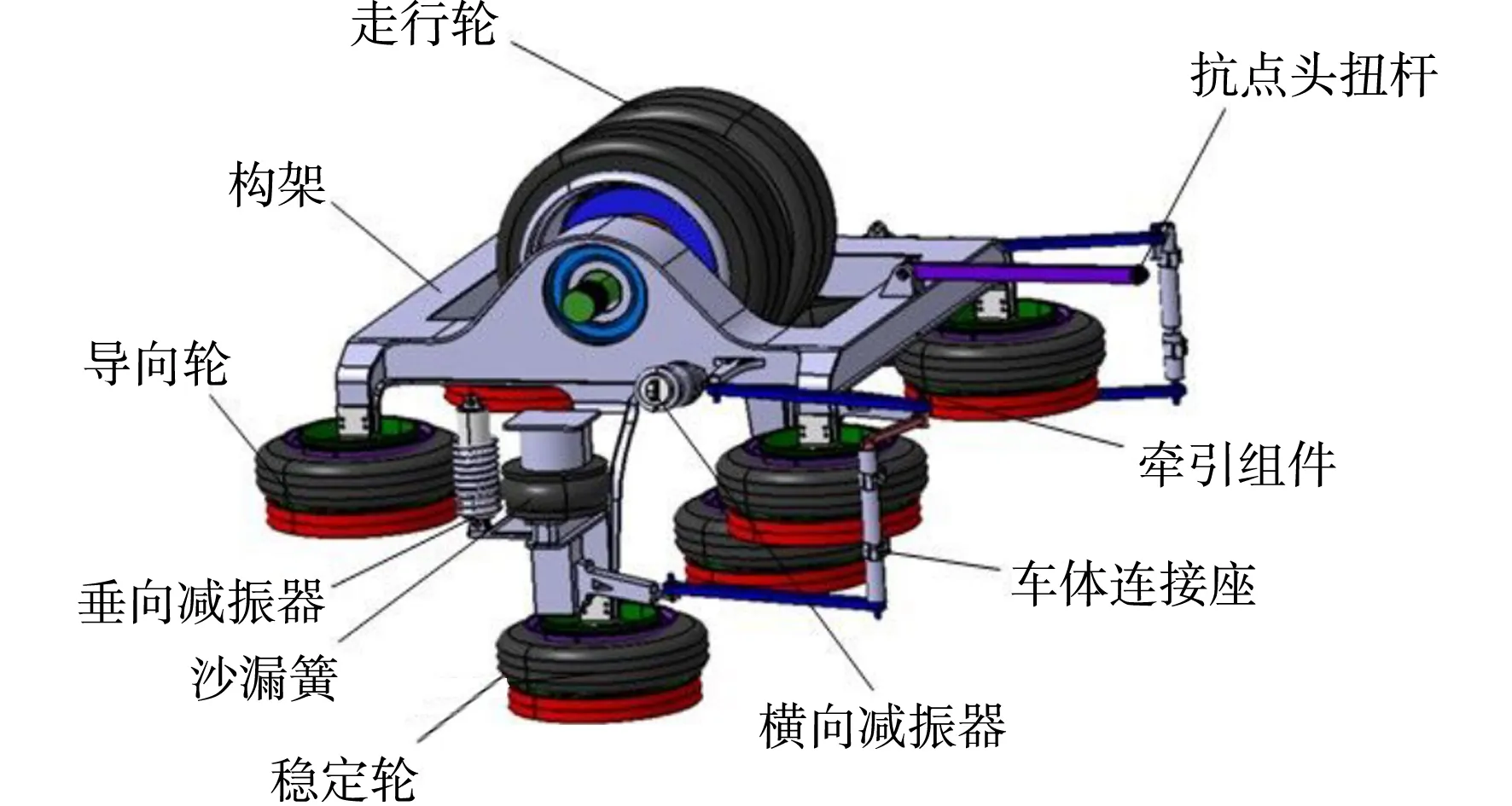
图1 单轴式转向架

在车辆行驶过程中，一部分牵引力通过牵引组件传递，牵引力从转向架构架传递给牵引连杆，再通过牵引连杆上的车体连接座传递给车体；另一部分牵引力则通过抗点头扭杆传递，牵引力从与转向架构架相连的抗点头扭杆一端，传递给与车体相连的另一端；前、后转向架的空间杆系结构对称布置.走行部件与车体之间通过横向和垂向减振器与油压弹簧相连接，垂向和横向减振器一前一后斜对称布置于转向架左右两侧.单轴式单轨车辆的垂向载荷从车体经一定垂向刚度的沙漏簧传递到转向架；横向载荷从车体经一定横向刚度的沙漏簧和牵引杆系传递到转向架；纵向载荷经一定纵向刚度的牵引杆系从转向架传递到车体[7].

1.2 车辆动力学模型的建立

单轴式单轨车辆的实际结构较为复杂，不仅各部件间存在相互作用力和相对运动，而且车轮与轨道梁之间也存在复杂的轮轨耦合关系.有的部件可视为刚体，有的部件因具有特殊的非线性特性，可视为弹性体.在建立单轴式单轨车辆动力学模型时，对动力学性能影响较大的部件应尽可能与实际情况相符，而对动力学性能影响较小的部件可以进行适当的假设和简化[8].因此，文中做以下3点假设.1)忽略车体和前、后转向架等部件的弹性变形，将其视为刚体.2)不考虑轨道梁弹性变形，走行轮与轨道梁顶部始终保持接触状态.3)忽略单轴式单轨车辆中悬挂元件结构制造上的误差，假定整个单轴式单轨车辆中各走行轮、导向轮和稳定轮结构对称，且对应的动力学参数相等.

单轴式单轨车辆的动力学拓扑结构，如图2所示.图2中：γ，β为自由度(DOF).车体与前、后转向架构架各有5个自由度，分别为横摆、浮沉、侧滚、点头和摇头，而走行轮只有相对于车轴绕y轴旋转1个自由度，在SIMPACK动力学仿真软件中，水平轮并非轮胎，故通过弹簧-阻尼的接触力元的方式进行模拟，不存在水平轮摇头的自由度.因此，单节单轴式单轨车辆模型的自由度为19个.

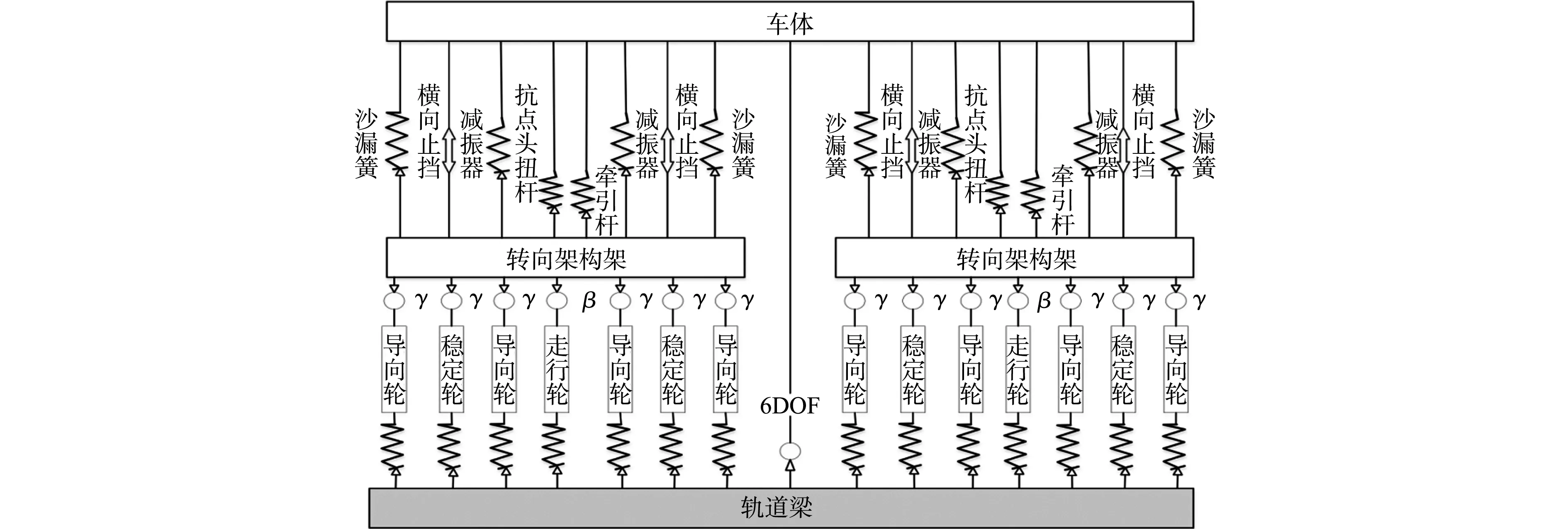
图2 单轴式单轨车辆的动力学拓扑结构

基于单轴式单轨车辆的动力学拓扑结构，通过SIMPACK动力学仿真软件建立单节单轴式单轨车辆模型，以单轴式单轨车辆(车速v=30 km·h-1)通过最小曲线半径为100 m线路时的工况为研究对象，其动力学模型，如图3所示.

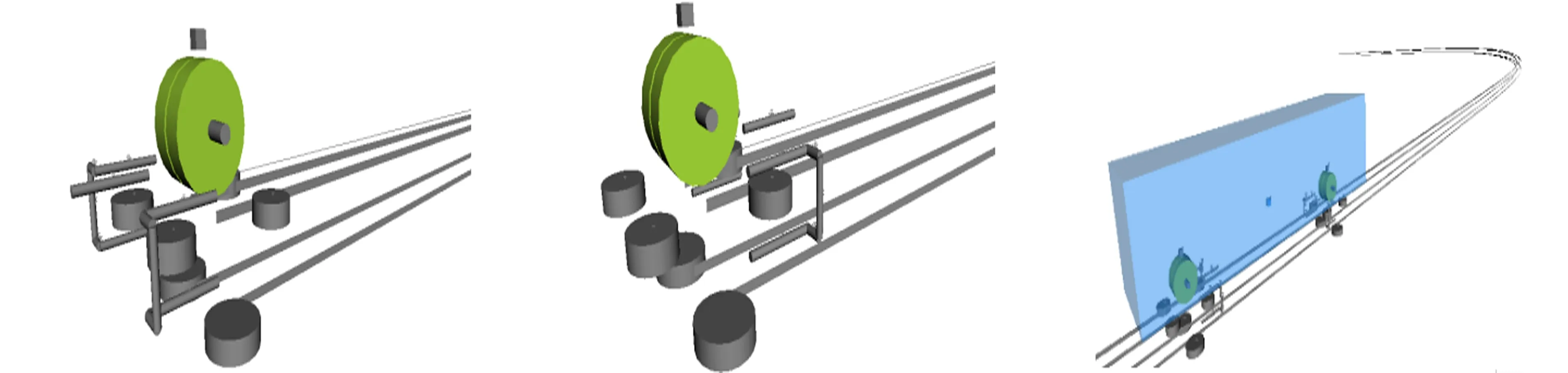
(a)前转向架子模型 (b)后转向架子模型 (c)整车模型

2 灵敏度分析

2.1 灵敏度分析参数

通过Isight多目标优化软件建立单轴式单轨车辆灵敏度分析模型，选用16个参数进行分析，并对其上、下限进行设置.悬挂系统参数的设置，如表1所示.

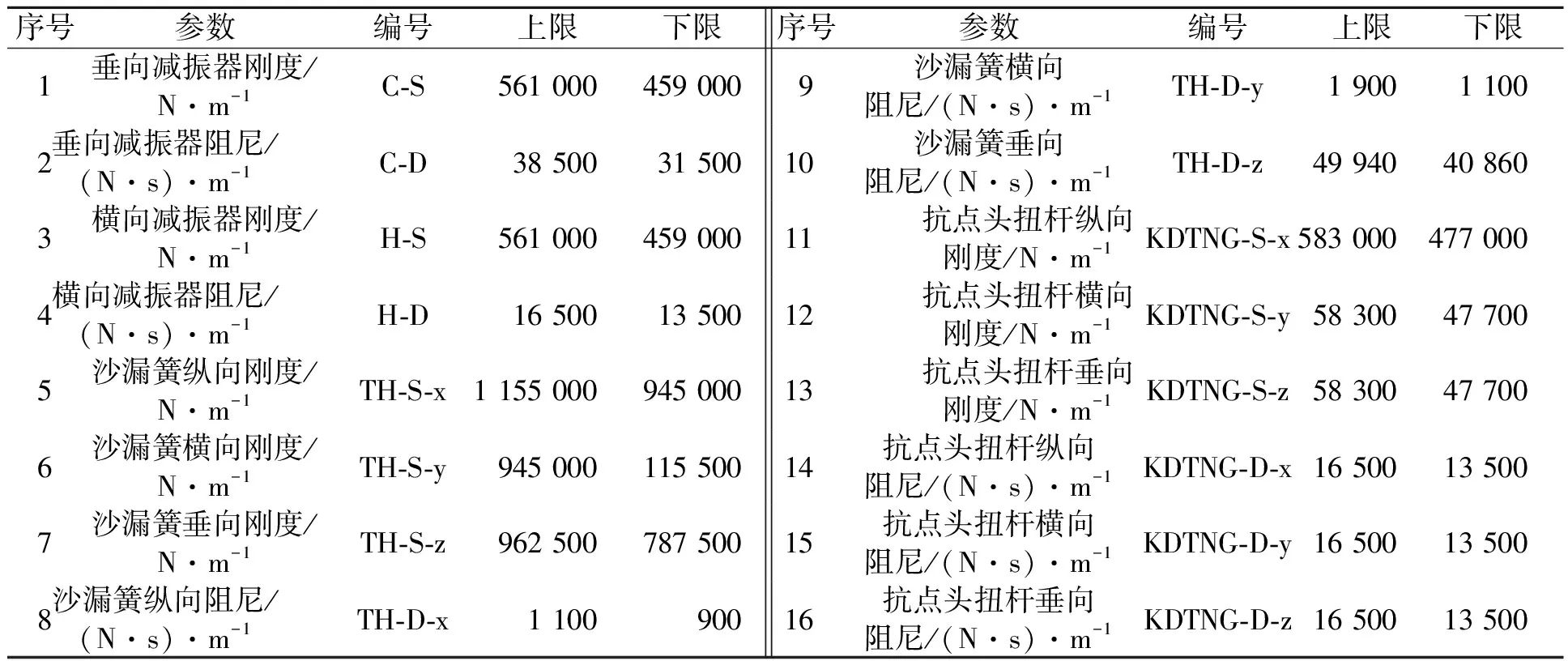
表1 悬挂系统参数的设置

灵敏度分析是指分析一个系统的状态或输出的变化对系统参数变化的敏感程度.一般通过逐一改变参数的数值来解释关键指标受参数变动影响的规律[9].通过对输入参数进行分析，筛选出对目标函数影响较大的参数，再对其进行针对性的优化设计，从而提高工作效率，节省时间.

2.2 优化目标选择

跨座式单轨车辆的导向力矩(M)是衡量车辆曲线通过性能的指标，走行轮侧偏力(Fty)是衡量走行轮偏磨损程度的指标.为了提高车辆曲线通过性能，降低走行轮偏磨损程度，将单轴式单轨车辆的导向力矩与走行轮侧偏力作为优化目标.

单轴式单轨车辆的结构特殊，当车辆过弯道时，轨道梁与导向轮之间的相互耦合作用产生使走行轮发生径向调节的导向力矩，迫使车辆沿既定的轨道运行[10].车辆通过弯道时，最大导向力矩Mmax的计算公式为

(1)

式(1)中：Fd，1～Fd，4分别为4个导向轮的径向力；L1为导向轮的纵向距离.

跨座式单轨车辆过弯时转向架受力示意图，如图4所示.图4中：Fw，1，Fw，2为左、右稳定轮横向力；Fk，1，Fk，2为左、右沙漏簧纵向力；Fty，1，Fty，2为左、右走行轮侧偏力.由图4可知：当车辆过弯时转向架的导向力矩越小，则车辆的曲线通过性越好；走行轮偏磨损程度较低，有利于提高走行轮的使用寿命.

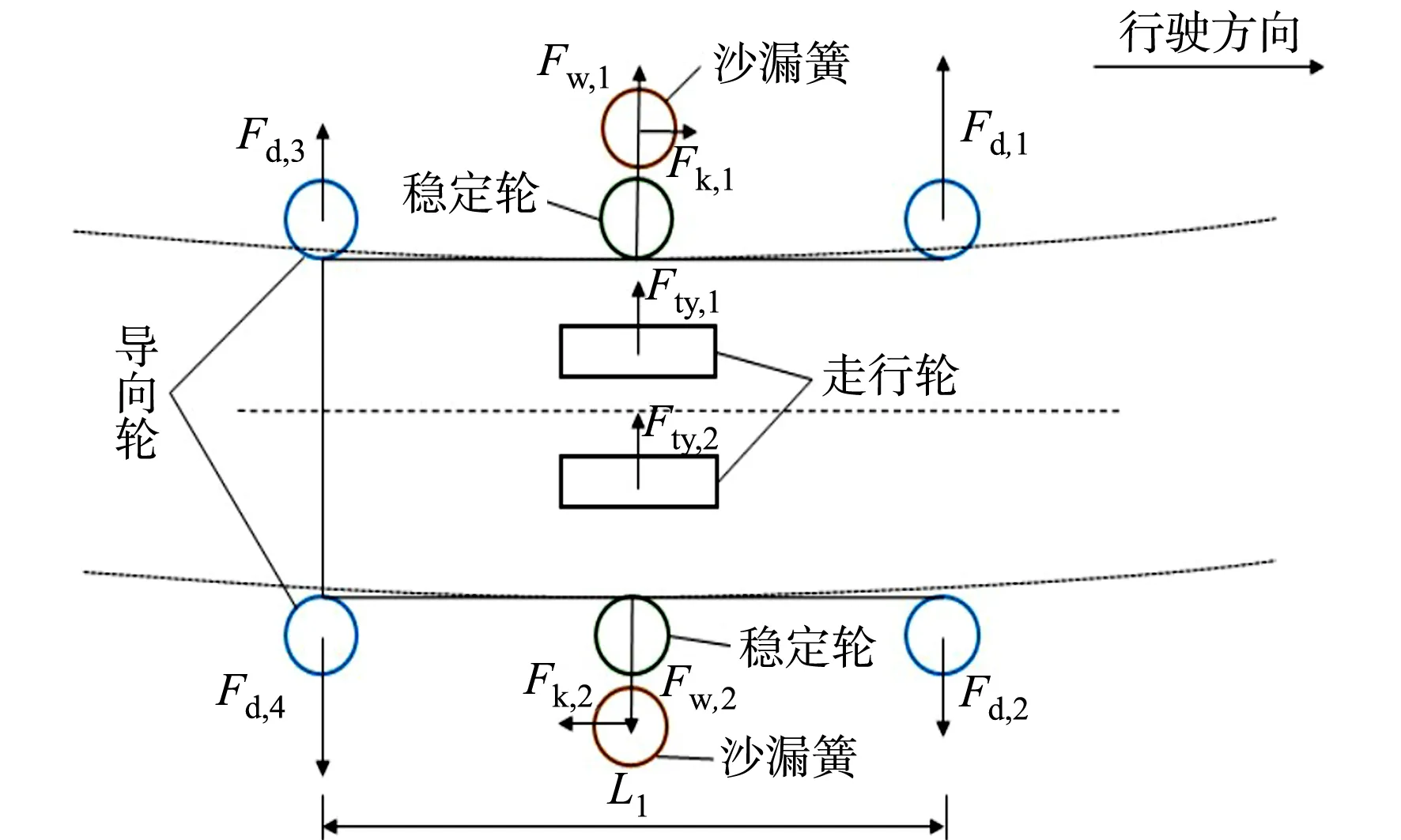
图4 车辆过弯时转向架受力示意图

2.3 灵敏度结果分析

为了筛选出对跨座式单轨车辆目标函数影响显著的参数，对悬挂系统参数进行灵敏度分析.结果表明，对导向力矩影响最为明显的4个参数依次为沙漏簧横向刚度>抗点头扭杆横向刚度>横向减振器刚度>垂向减振器刚度.导向力矩灵敏度分析柱状图，如图5所示.图5中：正值表示正相关；负值表示负相关；a为灵敏度.

图5 导向力矩灵敏度分析柱状图 图6 走行轮侧偏力灵敏度分析柱状图

对走行轮侧偏力影响最为明显的4个参数依次为沙漏簧横向刚度>抗点头扭杆垂向阻尼>抗点头扭杆横向阻尼>横向减振器刚度.走行轮侧偏力灵敏度分析柱状图，如图6所示.

3 多目标优化分析

3.1 优化参数的取值范围

对单轴式单轨车辆悬挂系统参数进行灵敏度分析，选取横向减振器刚度、垂向减振器刚度、沙漏簧横向刚度、抗点头扭杆横向刚度、抗点头扭杆横向阻尼、抗点头扭杆垂向刚度等对目标函数影响显著的6个优化参数，以车体侧滚角不超过0.02 rad和水平轮最大径向力不超过20 kN为约束条件[11].优化参数的设置，如表2所示.

3.2 优化模型搭建

采用Isight多目标优化软件，通过改进型遗传算法进行多目标优化分析.首先，随机产生规模为N的初始化种群，非支配排序后，通过遗传算法的选择、交叉、变异3个基本操作，得到第1代子群；然后，从第2代开始，将父代个体与子代个体合并；再次，进行快速非支配排序，并对每个非支配层中的个体进行拥挤度排序，依据非支配关系及个体的拥挤度，选取合适的个体组成新的父代种群；最后，通过遗传算法的基本操作产生新的子代种群，依此类推，直到满足程序结束的条件[12].

改进型遗传算法流程图，如图7所示.

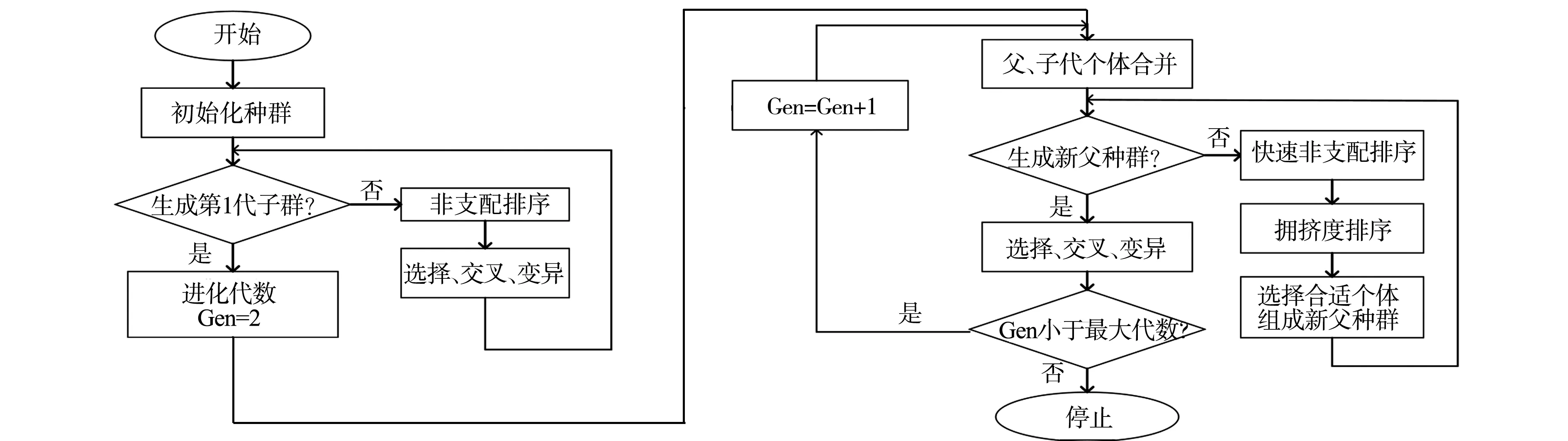
图7 改进型遗传算法流程图

搭建优化分析模型，首先，设置Isight多目标优化软件与SIMPACK动力学仿真软件的接口.然后，将单轴式单轨车辆动力学模型需要的参数转化为优化模型中的设计变量，调用单轴式单轨车辆动力学模型，并进行第1次仿真计算；Isight多目标优化软件通过改进型遗传算法对输入参数进行修改，并准备下一次计算.计算完成后，Isight多目标优化软件对获得的目标值进行评价，判断是否满足终止条件，如果没有，则重新进行上述迭代步骤[13-16].优化分析模型，如图8所示.

图8 优化分析模型

基于搭建的优化分析模型，迭代1 600次(编号为0～1 600号)后，导向力矩与走行轮侧偏力均收敛，具体迭代过程，如图9～12所示.图9～12中：n为迭代步数.在全面分析优化目标的前提下[17-19]，从帕累托(Pareto)优化解中挑选出3种比较理想的方案(462号，672号，926号)，如表3所示.由表3可知：若以导向力矩为最优目标时，672号方案较好，462号方案较差；若以走行轮侧偏力为最优目标时，462号方案较好，926号方案较差.

表3 优化方案分析

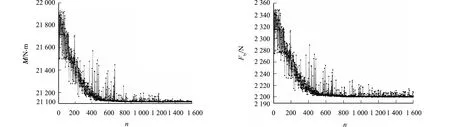
图9 导向力矩的迭代过程 图10 走行轮侧偏力迭代过程

综上可知，672号方案导向力矩最小，走行轮侧偏力也较小.因此，选用672号方案为最终优化方案.导向力矩初始值为21 927 N·m，优化后为21 116 N·m，较优化前减少了3.67%；走行轮侧偏力初始值为2 348 N，优化后为2 200 N，较优化前减小6.30%.因此，文中方法可达到优化目的，在一定程度上改善了单轴式单轨车辆的曲线通过性能[20-21].

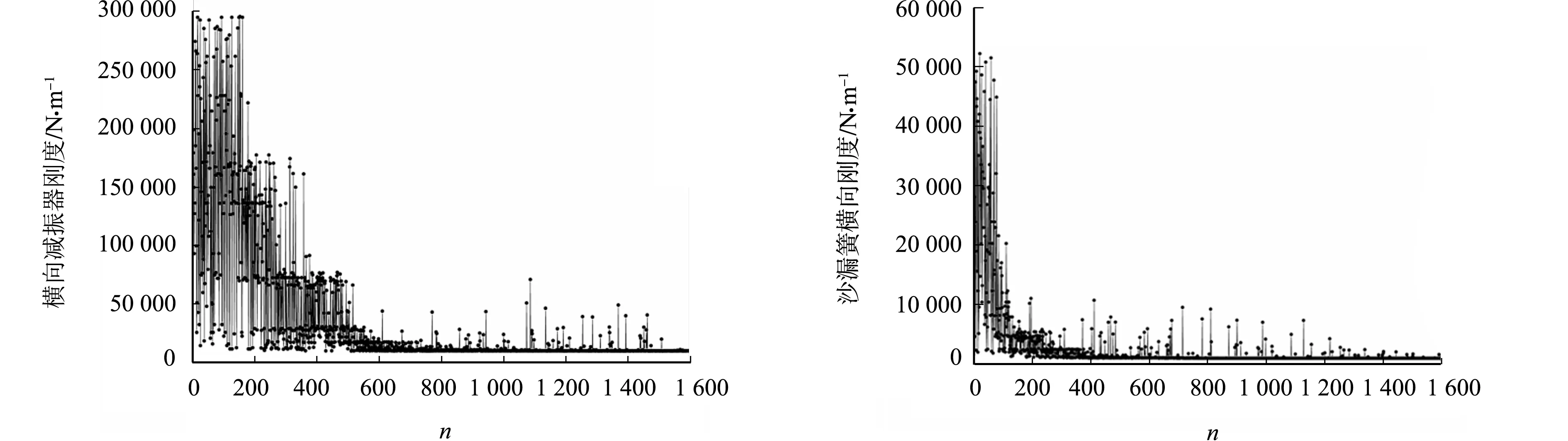
图11 横向减振器刚度迭代过程 图12 沙漏簧横向刚度迭代过程

4 结束语

对新型单轴式单轨车辆的曲线通过性能进行分析，运用SIMPACK动力学仿真软件与Isight多目标优化软件联合优化仿真，根据单轴式单轨车辆动力学拓扑结构，建立相应的单轴式单轨车辆动力学模型，对车辆悬挂系统参数灵敏度进行分析，筛选出对单轴式单轨车辆过弯时的导向力矩和走行轮侧偏力影响较大的参数，并对这些参数进行多目标优化分析，在保证车体侧滚角不超过0.02 rad和水平轮最大径向力不超过20 kN的前提下，单轴式单轨车辆过弯时的导向力矩比优化前减少了3.67%，走行轮侧偏力比优化前减少了6.30%.文中方法在一定程度上改善了单轴式单轨车辆的曲线通过性能.