异形汽车座椅弹簧的刚度及应力分析

林柄宏，黄志辉，王玉辉，穆云飞

(1.西南交通大学 牵引动力国家重点实验室，四川 成都 610031；2.湖南铁路科技职业技术学院，湖南 株洲 412006)

弹簧具有能够缓和冲击、储放能量和传递动力等特性，因此被广泛应用于各个领域.肖光育等[1]针对汽车悬架弹簧刚度恒定带来整车姿态负角，舒适性差等问题，设计了一种腰鼓型变刚度弹簧，能显著提高汽车的动态性能且节省安装空间.冯金芝等[2]和方子帆等[3]基于弹簧串联和并圈理论，提出多段式汽车悬架螺旋弹簧的设计思路，分析了弹簧关键参数对弹簧特性的影响并利用有限元软件进行分析验证.周凯林等[4]利用ANSYS建立了地铁车辆弹簧的几何模型，对弹簧的垂向刚度及横向刚度进行有限元计算，并与理论计算结果进行对比.周勇等[5]基于接触理论，利用有限元软件对断路器拉伸弹簧刚度和冲击载荷作用下弹簧的应力分布进行计算和分析.李红艳[6]采用ANSYS的APDL语言建立螺旋弹簧的几何模型，并对弹簧进行强度分析和疲劳寿命校核.

汽车椅弹簧作为车体与乘客间相互作用的媒介，其可靠性也影响使用者的体验.陈积云[7]提出两种变刚度汽车坐垫弹簧方案，并针对各方案进行了舒适性研究，变螺旋角的圆锥弹簧方案更优.文中以某型异形汽车椅弹簧为研究对象，针对其刚度特性及应力进行理论计算，并利用Hypermesh与ANSYS联合仿真进行分析与验证.

1 汽车椅弹簧的理论分析

1.1 汽车椅弹簧基本参数

异形汽车椅弹簧为圆柱拉伸弹簧，用于汽车座椅靠背调节.现有车型的汽车座椅靠背调节弹簧多为圆锥弹簧或卷簧，而该弹簧中间段簧圈中径一致，接近端部处中径逐渐增大后又减小.弹簧簧圈并紧，经过热处理及喷丸等工艺处理消除应力后，通过起耳完成整个结构.图1为弹簧的2维尺寸标注图.

图1 汽车椅弹簧2维尺寸标注图

异形汽车椅弹簧的几何参数，如表1所示.表1中：d为簧丝直径；D为弹簧中径；D1为弹簧内径；L1为钩环中心距离；R1为钩环半径；n为有效圈数.

表1 汽车椅弹簧的几何参数

汽车椅弹簧两端簧圈中径均匀变化，弹簧最大簧圈中径为32.8 mm.汽车椅弹簧采用琴钢丝制造，其材料属性如表2所示.表2中:E为弹性模量；ρ为密度；μ为泊松比；σs为屈服强度.

表2 汽车椅弹簧的材料属性

1.2 汽车椅弹簧刚度理论计算

根据国家标准GB/T 23935-2009《圆柱螺旋弹簧》可知，拉伸弹簧的刚度计算应与压缩弹簧一致[8].圆柱螺旋弹簧的垂向刚度计算式为

(1)

式(1)中：G为材料的剪切模量，GPa；n为有效圈数；D为弹簧中径，mm.

将汽车椅弹簧参数代入式(1)中，其中G取值为77.0 GPa，n取值为68圈，弹簧中径按中间段弹簧中径简化，计算可得弹簧垂向刚度为621.55 N·m-1.

实际弹簧结构中弹簧中径并未完全一致，所以上式计算得出理论值误差较大.为了提高理论计算的准确度，基于弹簧串联理论即弹簧刚度可视为多段弹簧串联，满足串联弹簧刚度计算公式为

(2)

可将弹簧视为由四段锥形弹簧和一段圆柱螺旋弹簧串联而成，如图2所示.

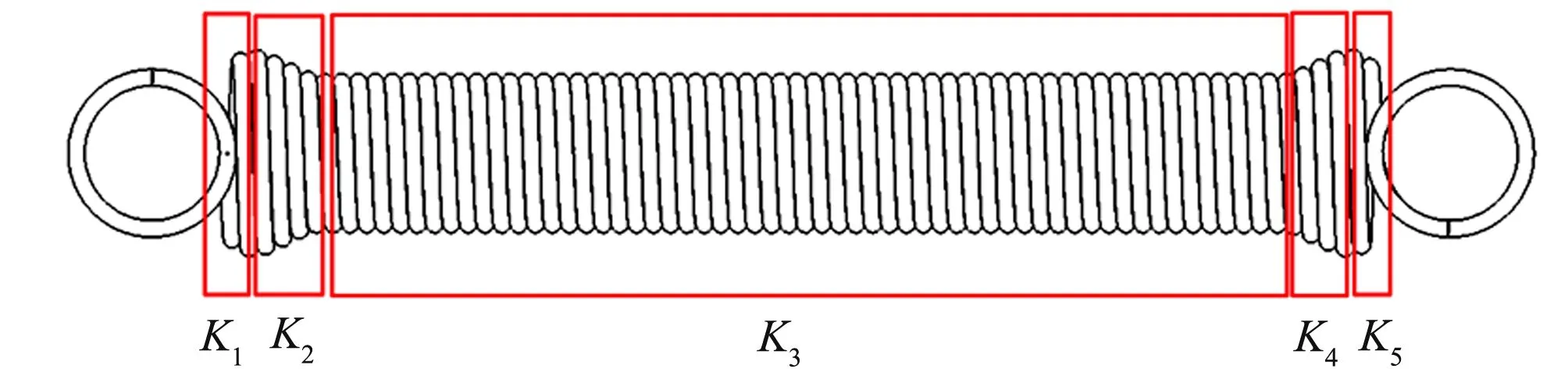
图2 汽车椅弹簧刚度组成示意图

由于K1，K2段分别与K4，K5段相同，所以汽车椅弹簧刚度可表示为

(3)

K3段弹簧刚度按式(1)进行计算，圆锥弹簧的刚度计算公式[9]为

(4)

式(4)中：R1为圆锥弹簧小端中径之半，mm；R2为圆锥弹簧大端中径之半，mm.

将弹簧端部视为由两个锥形弹簧构成，如图3所示.图3中的两个锥形弹簧小端半径分别取14.1和12.05 mm，即R1′=14.1 mm，R1=12.05 mm，R2=16.1 mm.

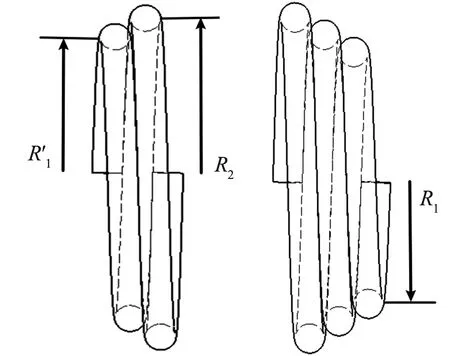
图3 汽车椅弹簧端部示意图

经式(1)，式(3)和式(5)计算，可得出汽车椅弹簧的近似刚度为558.66 N·m-1.

1.3 汽车椅弹簧的应力计算

当弹簧受到轴向载荷时，在通过弹簧轴线的平面所截得的弹簧材料斜截面上的作用有扭矩和径向力，而在弹簧变形的同时会产生弯曲应力和剪切应力.

圆柱拉伸弹簧的切应力计算公式为

(5)

式(5)中：F为轴向载荷，N；K′为曲度因数.其中，K′的计算式为

(6)

式(6)中：C为旋绕比，C=D/d.

汽车椅弹簧满载工况为(177.9±17.79)N.此处，按(177.9+17.79)N计算满载工况下弹簧切应力的大小为640.08 MPa.

2 汽车椅弹簧的有限元分析

2.1 弹簧刚度有限元计算

利用CATIA软件中创成式设计模块对弹簧进行建模，其中的曲线光顺功能可以使中心曲线平滑过渡消除拐点.将3维模型导入Hypermesh中进行模型简化、单元离散和工况加载.模型共包含节点281 178个，单元219 424个，其中单元最小尺寸为0.33 mm.

在进行有限元计算时，对汽车椅弹簧进行前处理，即在弹簧的一端钩环施加全约束，另一端钩环处施加轴向力F，如图4所示.前处理完成后导入至ANSYS中进行多种工况仿真，不同载荷对应的变形量，如表3所示.表3中：F为轴向载荷；Δ为轴向变形量；K为刚度.

图4 汽车椅弹簧受力及约束位置

表3 汽车椅弹簧轴向载荷与轴向变形量

由表3数据可得到汽车椅弹簧轴向力与位移的关系，如图5所示.从图5可知：弹簧的轴向载荷与轴向位移呈近似线性关系，弹簧的仿真刚度为509.24 N·m-1，与理论计算结果558.66 N·m-1相差9.70%，相对误差小于10%，仿真计算结果具有一定的可靠性.

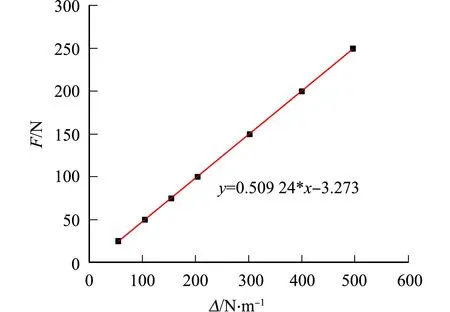
图5 汽车椅弹簧轴向载荷与轴向变形量线性拟合曲线

在进行不同轴向载荷仿真时发现，汽车椅弹簧的刚度随着轴向载荷的变化而发生小幅度变化.这是由于弹簧在受轴向力时，弹簧中径随着轴向力的增大而减小，并且由于弹簧端部簧圈中径较大，较弹簧中部变形量更大，簧圈中径变化更为明显.汽车椅弹簧在不同轴向载荷下的变形，如图6所示.从图6可知：当轴向载荷增大到177.9 N时，弹簧中径接近于一致.根据式(1)可知，弹簧中径随着弹簧轴向变形量的增大而减小，因此弹簧刚度会发生小幅度变化.

在实际运用中，同样要求汽车椅弹簧刚度能小幅度改变.当座椅靠背调节量较小时，弹簧刚度小方便调节并能提供一定的舒适性；而当座椅靠背调节量较大时，使弹簧刚度变大在小变形量的情况下，提供合适的力具有一定的稳定性.

2.2 汽车椅弹簧的应力分析

汽车椅弹簧作为关键部件，要保证使用安全性，应对该弹簧进行应力分析.若汽车椅弹簧的理论切应力值按照式(5)计算得出，式中的中径按统一中径简化计算，所造成理论与仿真结果相差较大.因此，需要对切应力计算公式加以修正.

由于该汽车椅弹簧两端钩环偏心设置，在所受拉力相同的情况下，所受力矩与标准中的弹簧相差一倍，即在所受拉力相同的情况下，力臂正好是式(5)中的2倍.考虑到中径在拉伸过程中逐渐减小的影响，需要对式(5)进行修正，添加修正系数β.即

(7)

由表4中可知：在添加修正系数后，理论切应力值与仿真计算得到的切应力值比较接近，最大相差9.44%，相对误差小于10%，证明修正系数是合理的.

2.3 汽车椅弹簧的强度校核

该汽车椅弹簧采用南韩琴钢丝制造，材料的强度极限为σb=2 051 MPa，屈服极限为τs=σb-150=1 901 MPa.对汽车椅弹簧静强度进行验算[10]，其计算式为

(8)

式(8)中：S为弹簧的安全系数；τs为弹簧材料的屈服极限；τmax为最大工作载荷所产生的最大切应力；SP为许用安全系数.

最大载荷工况按(177.9+17.79)N进行计算，可得最大剪切应力为851.1 MPa，位于弹簧簧圈端部远离钩环的一侧，如图7所示.

图7 最大载荷工况下的剪切应力云图

弹簧在满载工况下的最大应力为1 477.28 MPa，小于弹簧材料的屈服极限1 901 MPa，且按照式(8)计算得到弹簧的静强度安全系数为2.2，因此汽车椅弹簧满足强度要求.

3 结束语

通过对该弹簧进行理论和有限元分析，可得到以下4点主要结论.

1)国家标准GB/T 23935-2009《圆柱螺旋弹簧》中的垂向刚度计算公式得出的理论值与仿真结果相差较大，不适用于变中径弹簧；基于弹簧串联理论计算得到的刚度值更切合实际.

2)弹簧轴向载荷与轴向变形量呈近似线性关系，刚度随着轴向载荷的增大而小幅增大，满足实际应用中的特性要求.

3)利用Hypermesh与ANSYS联合仿真对汽车椅弹簧进行应力分析，针对标准中的切应力计算公式提出了合理的修正系数，所得到的结果更加合理.

4)在满载工况下，汽车椅弹簧能满足强度要求.