采用AHP-KCA的主动悬架LQG控制器设计
赵健,柳江,李明星,袁策
(青岛理工大学 机械与汽车工程学院,山东 青岛 266520)
汽车被动悬架存在构型相同则性能特征必然相同的桎梏,不能适应多变的路况,因而主动悬架成为研究的重点.控制策略是主动悬架研究的核心,不同的控制算法应用在悬架上取得的效果有所不同[1-4].线性二次高斯(linear-quadratic-Gaussian,LQG)算法作为一种较完善的控制算法,在悬架减振方面应用广泛,主动悬架控制器常采用该算法提升车辆性能.LQG控制器设计的关键在于各性能指标加权系数的选取,文献[5-7]采用试凑法确定加权系数,原理简单,但调试加权系数耗费时间较长且适应性较差.文献[8-9]利用层次分析法(analytic hierarchy process,AHP)求出2自由度和4自由度主动悬架各性能指标的加权系数.文献[10-11]利用遗传算法(genetic algorithm,GA)求出2自由度和7自由度主动悬架性能指标的加权系数.李鑫军等[12]将AHP和GA相结合,求得加权系数.但上述文献中,AHP存在主观片面性较多、稳定性较差的缺点;而GA的问题则是初始搜索范围较差,未能考虑各性能指标数量级的差异.因此,本文提出一种新的权值优化方案,将K均值聚类算法(K-means clustering algorithm,KCA)引入到加权系数的优化中,得出更合适的加权系数,从而提升车辆悬架的性能.
1 2自由度车辆模型
1.1 路面模型的建立
滤波白噪声生成随机路面输入模型为
(1)
式(1)中:zq为路面位移,m;f0为下截止的频率,Hz;G0为路面的不平度系数,m3·r-1;u0为车辆的前进速度,m·s-1;w为数学期望为0的高斯白噪声.
1.2 2自由度1/4车辆悬架模型的建立
建立2自由度1/4车辆模型,如图1所示.图1中:mb为车身质量;mw为车轮质量;ks为悬架刚度;kt为轮胎刚度;f为悬架主动控制力;cs为悬架阻尼系数;zb为车身位移;zw为车轮位移;zq为路面位移.
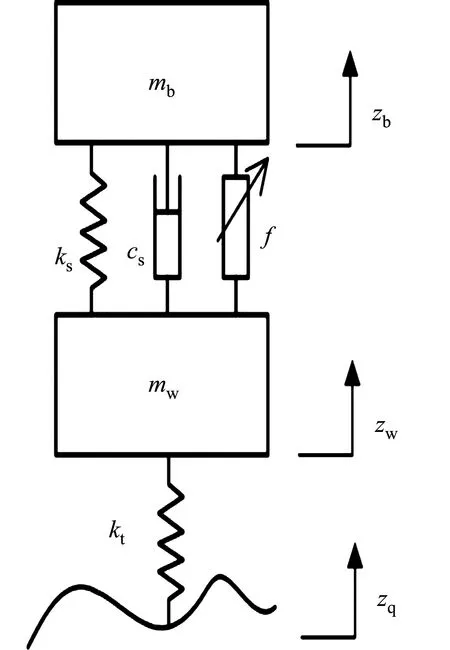
图1 2自由度1/4车辆模型
车辆模型的动力学方程为
(2)
(3)
1.3 系统状态方程
1/4车辆模型的车身加速度、轮胎动位移和悬架动行程是主要的悬架性能指标,因此系统的状态变量X和输出变量Y选取为
(4)
则系统的状态空间方程为
(5)
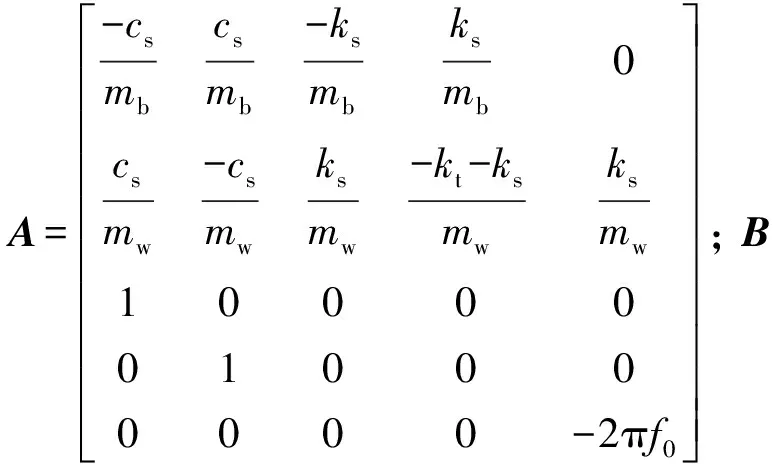
2 主动悬架LQG控制器的设计
在汽车行驶过程中,既要考虑车辆平顺性,又要保证行车安全性,同时还要避免悬架动挠度过大.因此,性能指标函数J表达式为
(6)
式(6)中:q1,q2和q3分别是各性能指标的加权系数.
根据最优控制理论,式(6)为
(7)
式(7)中:Q,R分别是状态变量及控制变量的加权矩阵;N是交叉项的权重.
由MATLAB软件中的lqr函数求出最优增益反馈矩阵K,即
[K,S′,E]=lqr(A,B,Q,R,N).
(8)
式(8)中:S′为Riccati方程解;E为系统特征值.
根据状态变量X在时刻t的瞬时值X(t),可求出作动器在时刻t的控制力U(t)为
U(t)=-KX(t).
(9)
3 基于AHP的控制器的仿真分析
3.1 基于AHP的确定加权系数

(10)
3.1.2 主观加权比例系数 1)构造性能指标间的判断矩阵H,设hi,j为指标i对指标j的重要性比值,hi,j性能指标间重要性比值如下:同等重要为1;略重要为3;比较重要为5;重要为7;很重要为9.若指标间重要性比值介于2个比值之间,则可依次取2,4,6,8.
2)求解各性能指标的权重排序向量W,根据判断矩阵H,可知H中各行元素的乘向量M为
(11)
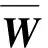
(12)
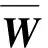
(13)
3)H的最大特征值λmax及一致性检验CR分别为
(14)
式(14)中:RI是H的随机一致性指标.
当n=3时,RI=0.52,将此值代入式(14),求解CR.若CR<0.1,则通过一致性检验,否则,需要对矩阵H进行一致性校正[13].
4)求解主观加权比例系数,以车身加速度为主要优化目标,令其主观加权系数γ1为1,则其他性能指标的主观加权系数为
W1/γ1=Wi/γi,i=1,2,…,n.
(15)
3.1.3 最终加权系数 由式(10)得出的同尺度量化比例系数βi及由式(15)得到的主观加权比例系数γi求得悬架各性能指标的最终加权系数qi,即
qi=βi×γi,i=1,2,…,n.
(16)
3.2 车辆模型的仿真输入参数
以某轿车为研究对象,车辆模型有关参数[14]如表1所示.

表1 车辆模型仿真输入参数
3.3 基于AHP的LQG控制器的仿真与分析
基于AHP优化的悬架性能仿真图,如图2所示.由判断矩阵H,再根据式(10)~(15)可得到3个性能指标的加权系数分别为q1=1,q2=1 130,q3=73 445.根据表1车辆模型输入仿真参数和3个加权系数,运行MATLAB/Simulink软件中的仿真模型.被动悬架的车身加速度、悬架动行程、轮胎动位移均方根值分别为1.266 9,0.012 4,0.004 5;采用AHP优化后的主动悬架的车身加速度、悬架动行程、轮胎动位移均方根值分别为1.096 4,0.010 2,0.004 7.
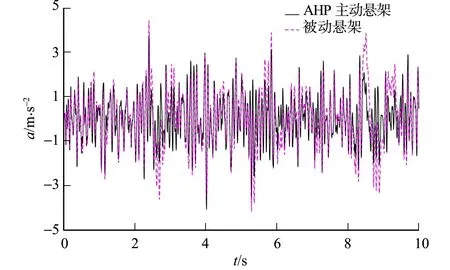
(a)车身加速度
由图2可知:相较于被动悬架,采用AHP主动悬架车身加速度的均方根值有明显的降低,减小了13.46%,有效地改善了汽车平顺性;悬架动行程减小17.74%,且完美符合设计的要求范围(±100 mm),降低了撞击悬架限位的概率;但是主、被动悬架的轮胎动位移的均方根值相差不大,说明主动悬架对轮胎动位移没有明显的控制效果.因此,LQG控制器的设计符合要求.
4 基于KCA的控制器的仿真分析
4.1 KCA样本的确定
为保证车身加速度的优化效果,令车身加速度的加权系数为q1=1,q2,q3为自变量.在MATLAB中,根据AHP提供的加权系数,采用Random随机函数进行仿真实验.设q2范围为[1 000,2 000],q3范围为[50 000,100 000],在此范围内各随机取15个数值.
加权系数q2,q3的随机取值在MATLAB软件表示为
(17)
运行函数后,得到
(18)
将q2,i,q3,i正交组合,q1=1,得到225组加权系数,代入到LQG控制器中进行仿真实验,得到主动悬架3个性能指标的均方根值RMS(a),RMS(S),RMS(s).记录仿真结果并按序编号,将其作为KCA聚类分析的样本,得到样本数据.
4.2 基于KCA的样本数据仿真与分析
4.2.1 KCA的设计与编程 KCA的输入包含N个数据集x和类簇的数目k;输出为k个类簇及每个类簇包含的样本个数及编号[15].
算法流程,如图3所示,具体有如下5个步骤.
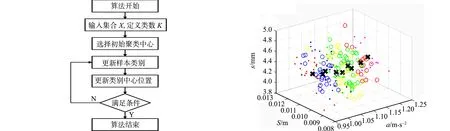
图3 KCA聚类流程 图4 聚类结果图
1)初始化.X为给定包含N个数据的集合;K为聚类的类数;初始聚类中心为在X中随机选取k个对象.
2)设定迭代终止条件.通常设置最大循环次数作为终止条件.
3)更新样本对象所属类.根据距离准则将数据对象分配到距离最接近的类.
4)更新类的中心位置.将每一类的平均向量作为下次迭代的聚类中心.
5)重复步骤3)~4),当满足步骤2)中的迭代终止条件时,完成聚类.
4.2.2 KCA的聚类结果分析 在MATLAB软件中编写并运行KCA程序,根据悬架性能指标相似度的不同,样本划分为9类,得到聚类结果如图4所示.
由于主动悬架3个性能指标数量级和单位的差异性,无法直接叠加,为了获得LQG的综合控制效果,将悬架的3项指标归一化处理,得到综合控制指标L,即
(19)
式(19)中:Δi是主动悬架的性能指标;下标p是指被动悬架.
KCA聚类结果均值,如表2所示.表2中:M(i)(i=1,2,3,…,9)为i类均值;n为样本数.
由表2可知如下5点.1)对象最多的一类有32个样本,最少的一类包含12个样本.2)第2,9类的L最小,数值分别为2.616 5,2.632 0,综合控制效果最好.这两类的特征是RMS(a)较低,车辆乘坐舒适性相较于被动悬架改善较为明显.这两类权值系数取值分别为q2,2=1 435,q3,2=58 353;q2,9=1 373,q3,9=59 605,所选轿车模型悬架动行程的加权系数取值范围为1 350~1 450,轮胎动位移的加权系数取值范围为58 300~59 700时,车辆悬架获得最优性能.3)第3,4,6类的L居中,悬架性能表现较好;第1,5,7,8类的L值最大,数值均超过2.700 0,第5类L值接近2.800 0,悬架控制效果最差.此时,权值系数q2为1 550~1 750,q3为79 000~93 000,表明悬架动行程、轮胎动位移在加权系数都取较大值时,改善较大,但综合控制效果反而有所降低.4)a和L的改善效果具有一致性,两者成正相关.

表2 KCA聚类结果均值
车身加速度直观地体现汽车平顺性,根据RMS(a)的均值,再结合L,对9类数据进行分级处理,作出AHP-KCA分级表,如表3所示.

表3 AHP-KCA主动悬架分级表
表3是以机器学习替代专家主观选择的结果,对于不同车型都可以用AHP-KCA算法分析处理,为LQG控制器设计时权值的选择提供数据框架.从A级加权系数中选出控制效果最好的一组数据,q2=1 415,q3=59 300.由表3可知:9类样本数据分为3级,其中,第2,9类为A级,控制效果最佳;第3,4,6类为B级,控制效果较好;第1,5,7,8类为C级,控制效果差,但相较于被动悬架,这3级悬架性能都有所提升.
5 基于AHP-KCA主动悬架控制器的仿真分析
节3通过AHP求出了一组加权系数,在此基础上,节4利用KCA确定了另一组最优加权系数.结合这2组加权系数,运行Matlab/Simulink软件中的仿真模型,便可得到被动悬架与基于2种算法的主动悬架各性能仿真图,如图5所示.

(a)车身加速度
由图5(a)可知:相较于被动悬架,主动悬架显著降低了a的幅值,改善汽车的乘坐舒适性.由图5(b)可知:S明显的减小有效降低悬架击穿概率,使悬架工作空间得到更充分的利用.由图5(c)可知:采用AHP的主动悬架对s的控制效果不佳,但采用AHP-KCA的主动悬架降低s,改善行车安全性.
为了定量化分析,各性能指标均方根值,如表4所示.表4中:η1为AHP主动悬架性能指标变化率;η2为AHP-KCA主动悬架性能指标变化率.

表4 各性能指标均方根值
由表4可知:相较于被动悬架,2种算法设计的主动悬架均有效降低a,S的均方根值,且减小幅度都超过10.00%,验证了AHP比较矩阵中比值选择的合理性;AHP-KCA主动悬架比单一AHP主动悬架改善幅度更大,幅值减少超过20.00%,虽然AHP主动悬架对s没有起到积极效果,但AHP-KCA主动悬架降低s,减少幅度为8.90%,证明AHP-KCA结合算法的优越性.
为了验证AHP-KCA算法的可靠性,将AHP-KCA的仿真结果与已有文献作对比,对比结果如表5所示.表5中:η3为a的相对误差率;η4为S的相对误差率;η5为s的相对误差率.

表5 仿真结果对比
由表5可知:文中实验数据与已有文献实验数据的相对误差均较小,其中,a与文献[16]的实验数据误差为16.27%,S与文献[18]的实验数据相对误差为2.20%;与其他文献的仿真结果相比,文中相对误差也较小,3个性能指标的相对误差均在8%以下.因此,采用AHP-KCA算法的主动悬架起到不错的控制效果.
6 结论
1)在传统LQG算法基础上,增加AHP算法改善悬架的控制效果,并进一步引入KCA聚类,仿真结果证明:机器学习替代专家系统的方法是可行的,同时,其对于其他的基于经验的悬架控制算法也有一定的参考价值.
2)与被动悬架相比,采用AHP-KCA算法设计的LQG控制器,能显著提升汽车悬架性能(3个指标分别降低了20.03%,25.00%,8.90%).同时,将文中的仿真结果与其他文献的仿真或实验结果进行对比,相对误差均较小,证明了仿真结果的准确度,证明了AHP-KCA算法的可行性.
3)AHP-KCA算法给出了包含225组加权系数及悬架响应特性的数据集,并利用KCA分类分级,为LQG控制器设计中加权系数的确定提供了选择框架和理论指导.

