双回路变截面多棱锥钢管杆变形参数影响分析
冯 衡,吴海洋,徐 彬
( 中国电力工程顾问集团中南电力设计院有限公司,湖北 武汉 430071)
0 引言
变截面多棱锥钢管杆具有占地面积小、强度高、外形美观、安装方便的优点,适用于多回路、多电压等级同杆架设城市输电线路,被广泛应用于现代化城市电网建设中[1-4]。
IEC 60826-2017 对钢管杆的失效定义为两种形式:损坏极限状态和破坏极限状态。钢管杆有两种变形[5]。当钢管杆顶部产生1%的非弹性变形或者弹性变形影响导线安全间隙距离时,为损坏极限状态;钢管杆在受压或者受拉情况下,产生局部屈趋,则定义为破坏极限状态。
钢管杆属于空间薄壁壳体,在外荷载作用下,大变形引起损坏极限状态是常见的失效形式。如何在保证经济性的前提下,控制杆顶位移,是钢管杆设计中需重点考虑的问题[2]。
本文以巴基斯坦某城市输电工程中的设计实践为基础,通过实例计算,比较中国标准DL/T 5130-2001、欧盟标准BS EN 50341-2012、德国标准UNE-EN 50341-2-4-2019 中对钢管杆变形规定的差异;阐述钢管杆变形时表现出的二阶效应特征;研究主杆锥度、直径、壁厚、截面型式对钢管杆变形的影响。
1 不同规范对位移计算及限制的要求
主杆变形是钢管杆的一个重要指标。虽然钢管杆具有占地小的特点,但由于其自身截面刚度小,不可避免具有变形大的特征(如图1所示),大变形会在视觉上造成心理恐慌,同时也会造成导线对地距离减小,影响钢管杆的正常使用[3-5]。

图1 钢管杆变形实例
在DL/T 5130-2001《架空送电线路钢管杆设计技术规定》中明确规定[6],结构或构件的变形,按正常使用极限状态的要求,采用荷载的标准值和正常使用规定限值进行计算。

式中:δ钢为管杆变形的规定限值;CG为永久荷载的荷载效应系数;CQi为可变荷载的荷载效应系数;Gk为永久荷载标准值;Qik为第i项可变荷载标准值;ψ为可变荷载组合系数。
其中规定,钢管杆在荷载的长期效应组合(无冰、风速5 m/s 及年平均气温)作用下,钢管杆杆顶的最大挠度不应超过下列数值[6]:
1)直线杆不大于杆身高度的5‰;
2)转角杆和终端杆:110 kV ~220 kV 电压等级挠度不大于杆身高度的20‰。
在欧盟标准BS EN50341-2012 是采用以概率理论为基础的极限状态设计方法[7],使用荷载分项系数,基本计算理论公式如式(2)所示:

式中:Rd为材料性能设计值;f{……}是函数记号,也称功能函数;X1d、X2d、X1k、X2k……为影响该结构功能的各种荷载效应以及材料强度、杆件的几何尺寸等;γ m为分项系数;
该规范对钢管杆变形限值规定:在极限状态下,考虑二阶效应下,钢管杆的杆身变形不超过自身高度的8%。
德国标准UNE-EN 50341-2-4-2019 的设计方法与BS EN 50341-2012 基本相同[8],钢管变形按计算只考虑一阶效应。对变形限值建议如下:对于直线和转角杆,在90°大风或者90°大风与覆冰荷载组合下,杆顶变形不超过4%。
为比较不同规范的要求水平,以直线杆PT-132 为例,在相同荷载作用下,按照以上规范要求分别计算,比较变形大小[9]。
PT-132 是直线杆,设计档距为250 m,导线型式为1×240 mm2& 1×400 mm2铜导线,设计使用导线风压为89 kg/m2,钢管杆主杆采用正十二边形截面,横担采用正八边形,使用Q420 材质。设计工况包含正常大风工况、断线工况、安装工况。主杆与主杆之间采用套接,横担与主杆采用法兰连接形式,PT-132 的司令图如图2 所示。计算软件采用国际通用输电线路钢管杆设计软件PLS-Pole。

图2 PT-132司令图
钢管杆参数,如表1 所示:

表1 PT-132基本设计参数
计算结果比较如表2 所示:

表2 按照不同规范计算结果
分析以上计算结果,可以发现,对于相同尺寸的钢管杆,在相同外荷载作用下,均超过了DL/T 5130-2001 和UNE-EN 50341-2-4-2019规范中规定的变形限值,超出DL/T 5130-2001中规定的限值十分明显,但能够满足BS EN 50341-1:2012。由此可以得出结论,DL/T 5130-2001 和UNE-EN 50341-2-4-2019 规范中对变形的规定较为严格,而BS EN 50341-1:2012的规定较为宽松。
2 钢管杆变形规律
依据结构受力特点,输电线路单管杆的外形通常采用下大上小的变截面锥形,管壁厚度分段变化,因此单管杆属于变截面、变厚度的空间薄壁壳体结构。在水平风荷载作用下,单管杆受力通常会表现出非线性的特征。
线性计算情况下,钢管杆在水平荷载作用下,发生水平位移,不考虑垂直荷载产生附加弯矩对水平位移的影响。
非线性计算情况下,钢管杆在水平荷载作用下,发生水平位移,垂直荷载产生附加弯矩,附加弯矩再产生水平位移,通常我们称这种变化为钢管杆的二阶效应。
如图3 所示,由于水平力T1的作用,在杆身截面X1-X1产生弯矩MT,同时杆身发生位移,使垂直力V1与杆身截面X1-X1形成力臂,产生弯矩MV,使杆身形成进一步的位移。

图3 二阶效应示意图
查阅与钢管杆变形相关的文献,发现大多数文献研究了钢管杆分别在水平集中荷载、水平均布荷载、弯矩荷载作用下,杆身变形[10]。并认为,当以上荷载同时作用时,可直接代数叠加三种荷载作用下杆身的变形。上述研究成果,未考虑二阶效应的影响。
在我国规范DL/T 5130-2001《架空送电线路钢管杆设计技术规定》中6.1.4 条明确规定,钢管杆的计算应考虑变形的二次效应影响。为简化计算,规定可把水平荷载和垂直荷载产生的杆身弯矩乘上一个1.05 ~1.1 的放大系数来近似地考虑二次效应影响。
在UNE-EN 50341-2-4-2019 规范中,7.4.5.2 条明确说明,应考虑二阶效应,计算钢管杆的内力以及杆身弯矩。建议在一阶效应的基础上考虑5%的弯矩增量,即为二阶效应下截面弯矩值。
以PT-132 杆为例,运用PLS-Pole 软件,分别进行线性和非线性计算,杆身截面弯矩计算如图4 所示。
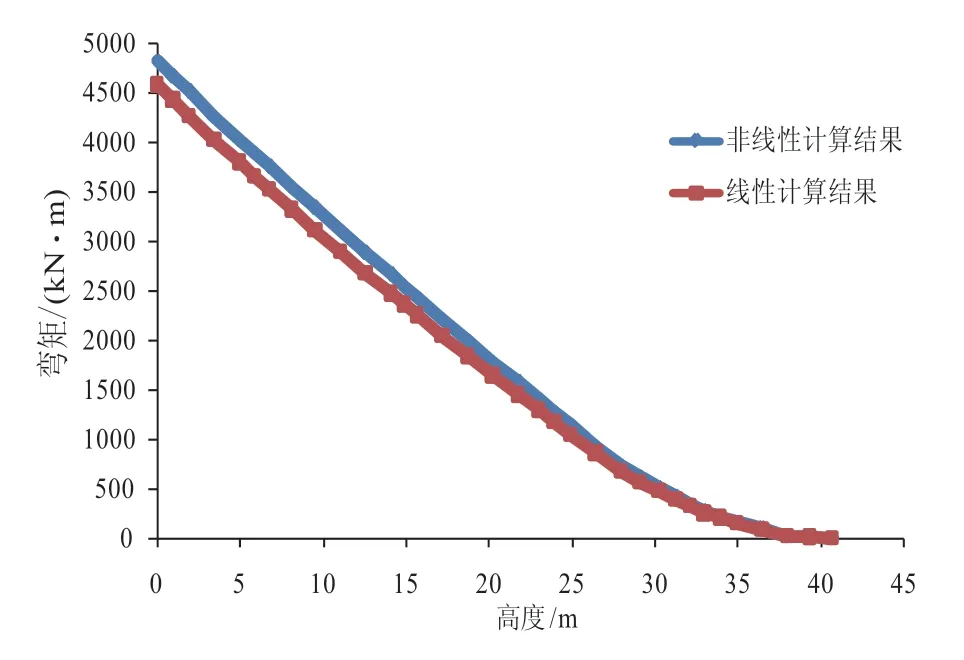
图4 线性和非线性弯矩图
由计算结果可以发现,非线性计算的弯矩比线性计算结果要大,平均增加了5.3%左右。
线性计算杆顶位移为2.451 m,考虑二阶效应的杆顶位移为2.641 m,增加了8%左右,如图5 所示。

图5 钢管杆线性和非线性变形图
3 钢管杆变形影响因素研究
钢管杆与其他输电设施的不同之处在于其变形在结构设计时起着决定性作用,影响变形的主要因素有主杆锥度、主杆径厚比、截面形状等[11-12]。在工程设计中,如何使钢管杆变形满足规程规范要求的同时,尽可能减轻杆塔重量,同时实现经济性和合理性,是摆在每一个设计人员面前的一道难题。
为了研究不同因素对钢管杆变形的影响,本文以直线杆PT-132 为例,进行计算分析。
3.1 主杆锥度影响
锥度是表征钢管杆杆壁倾斜程度的重要参数,其定义如下:

式中:D2为根径,D1为梢径,H为钢管杆刚度。
通常情况下,钢管杆自上而下有相同的锥度,如图6 所示。合理的杆身锥度应与杆身弯矩变化曲线的曲率决定,宜取弯矩曲率的外包络线坡度。
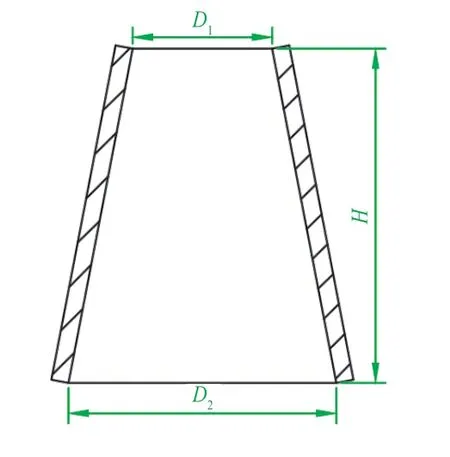
图6 锥形钢管杆示意图
为分析锥度对钢管杆变形的影响,本文以PT-132 塔型为例,计算了不同锥度情况下,杆身的变形,杆顶变形随锥度的变化曲线如图7 所示。

图7 杆顶变形与锥度变化关系曲线
由图7 可以发现,随着杆身锥度逐渐变大,杆身变形逐渐越小。在锥度增加35%的情况下,杆身位移减少了50%。由此可以知道,合理增加杆身锥度,是一种降低主杆变形的有效措施。
需要注意的是,虽然增加杆身锥度,能够减小杆身变形,但会增加钢管杆自身重量,使加工制造的精度降低,显得不经济。
3.2 主杆直径、壁厚对钢管杆变形的影响
钢管杆的刚度主要取决于截面的极惯性矩,对于正多边形的极惯性矩I[6]:

式中:D为钢管直径;t为钢管壁厚;α为极惯性系数。
提高主杆直径和杆壁厚度,能够有效提高截面刚度,从而减小钢管杆变形。主杆直径的提高、壁厚的增加,均会增加钢管杆的重量。
为研究钢管杆主杆直径与厚度对变形的影响,本文分别计算了相同锥度、相同梢径下,不同管径、不同壁厚情况下,钢管杆的变形,计算结果可参见表3 和表4。

表3 不同管径下变形计算值

表4 不同壁厚下变形计算值
分析表3 可知,随着钢管杆直径的增加,钢管杆变形明显减小,在主管底部直径增加26%的情况下,塔重增加19%,杆顶变形能够减小50%;分析表4 可知,随着钢管杆主杆壁厚增加,钢管杆主杆变形相应减小,在主杆壁厚全部增加4 mm 厚度的情况下,钢管杆重量增加32.8%,位移减小26%。
综合对比分析表3 和表4 可以发现,通过改变管径,能够更为有效减小钢管杆变形。
在城网建设中,钢管杆占地范围往往受限,在设计中应综合考虑管径和壁厚,以同时满足变形以及强度的要求。
3.3 主杆截面型式对钢管杆变形的影响
钢管杆截面为正多边形,不同形状截面的极惯性矩I与钢管杆平均直径D、管壁厚度t有关,如图8 所示。
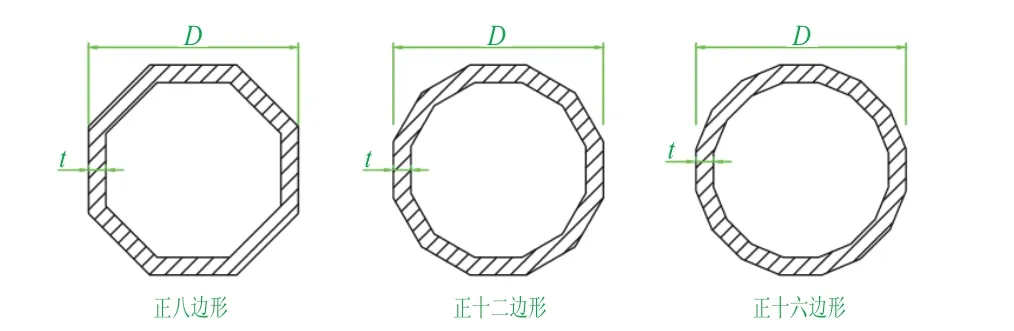
图8 钢管杆截面示意图
不同截面形式的刚度计算近似公式,列举如表5 所示。

表5 不同截面形式极惯性矩
分析可知,在具有相同平均直径D和管壁厚度的情况下,正八边形的极惯性矩最大,正十六边形的惯性矩较小。
本文以PT-132 杆塔为例,计算了平均直径相同情况下,不同截面型式的钢管杆变形,结果如表6 所示。

表6 不同截面钢管杆变形计算结果
由表6 数据分析可知,正八边形截面的杆顶位移值最小,正十六边形截面的杆顶位移值最大。在相同平均直径条件下,正十六变形的主杆变形比正八边形增加了9%,比正十二边形增加了2%。
可以发现,当其他边界条件确定时,钢管杆的变形与截面极惯性矩成反比,即同等条件下,截面极惯性矩越大,钢管杆变形越小。选用正八边形或者正十二边形比正十六边形或者圆形截面的效果要好。
4 结论
1) 通过理论分析,可以得出结论:DL/T 5130-2001 和UNE-EN 50341-2-4-2019 规范中对变形的规定较为严格,而BS EN 50341-1:2012的规定较为宽松;
2)分析了钢管杆在变形过程中具有非线性特征,对比了线性计算和非线性计算的结果差异;
3)通过算例计算,研究了不同因素对钢管杆变形的影响:
①随着杆身锥度逐渐变大,杆身变形逐渐越小,在锥度增加35%的情况下,杆身位移减少了50%。
②随着钢管杆直径和杆壁厚度的增加,钢管杆变形明显减小,在主管底部直径增加26%的情况下,塔重增加19%,变形能够减小50%,在主杆壁厚全部增加4 mm 厚度的情况下,钢管杆重量增加32%,位移减小26%;增加主杆直径是减小钢管杆位移更为有效的手段和措施;
③同等条件下,主杆截面极惯性矩越大,主杆变形越小。在相同平均直径条件下,正十六变形的主杆变形比正八边形增加了9%,比正十二边形增加了2%。
在实际工程设计中,应综合考虑影响钢管杆变形的各个因素,结合塔位周围的占地情况等,通过优化必选,确定最为合理、经济的设计方案。

