大豆散体材料的动力特性试验研究
静 行,陈慧芳,王晓雨
1.河南工业大学 土木工程学院,河南 郑州 450001
2.河南工业大学 河南省粮油仓储建筑与安全重点实验室,河南 郑州 450001
随着社会的发展和居民生活水平的提高,粮食需求呈刚性增长。大豆作为油脂、蛋白的重要原料,储存安全意义重大。近年来,各类粮食仓储设施在数量上和容量上都得到了迅猛发展,用于大豆储存的钢板筒仓直径和高度均超过了30 m,单仓仓容达到万吨以上。同时,仓储设施安全事故的报道也时有发生,如偏心卸料、钢筒仓屈曲、地震倒塌[1-2]等。粮食散体材料既是仓储设施的功能服务对象,也是仓储设施的一种重要荷载,其力学性质是研究粮食仓储设施结构行为与数值模拟的重要基础。
与土体等其他散粒体相似,粮堆在仓内围压约束下,也会表现出复杂的力学行为。《粮食钢板筒仓设计规范》(GB 50322—2011)给出了重力密度、内摩擦角、与仓壁的摩擦系数等粮食物料特性参数的经验数据供设计时选用,由于实际工程多样化、复杂化,又特别要求粮食的物料参数一般应通过试验测定。近年来,国内外学者针对粮食力学性质开展了一系列研究,李心平等[3]通过静态压缩试验分析了含水率对不同品种的玉米种子最大破裂力的影响,并研究了玉米种子在平放、立放、侧放状态下的裂纹发展规律。程绪铎等[4]通过应变控制式三轴试验测得玉米堆的弹性模量,并分析了围压、含水率等参数对玉米堆弹性模量的影响。许启铿等[5]通过试验分析了粒径、形状、含水率等因素对不同地区大豆散料的内摩擦角、散料与仓壁摩擦系数以及自然安息角等参数的影响。高连兴等[6]通过静态试验分析了不同含水率对大豆力学特性的影响,提出大豆弹性模量与含水率的函数模型。杜丽等[7]基于弹性力学理论,推导出静三轴压缩试验中压缩试样的解析解,并根据压缩试样的受力特点提出了求粮食泊松比的方法和计算公式。曾长女等[8-10]利用静三轴试验研究了小麦的强度特性及影响参数。李春娣等[11]通过Brookfield质构仪对不同含水率的大豆籽粒进行了压缩试验,建立了大豆籽粒弹性模量等力学特性参数与含水率的关系模型。杨作梅等[12-13]对不同含水率、储藏条件下稻谷籽粒的力学特性进行了研究。许启铿等[14-15]通过静三轴试验研究了小麦散体的应力-应变关系以及围压与弹性模量关系,提出不同围压下小麦粮堆压缩模量的表达式。静行等[16]通过直剪试验对不同垂直压力及剪切速率下大豆粮堆的强度和内摩擦特性进行了分析。Abdel-Rahim[2]在筒仓的地震响应分析中采用了 Duncan-Chang 非线性弹性模型反映粮食的力学性质。张丰尧等[17]通过建立大豆直剪试验离散元模型对大豆在不同剪切速率、仓壁材料及含水率因素下的抗剪强度变化进行了分析。李腾龙等[18]利用粮食静动直剪仪对大豆散料进行了单调、循环直剪试验,分析了竖向应力、循环剪切幅值、初始孔隙率对大豆剪切刚度和阻尼比的影响。
然而,针对粮食在动荷载下力学行为的研究成果还较少,难以满足粮仓结构动力分析与计算的需求。因此,作者借鉴土动力学理论及动三轴试验,对大豆散体材料的动力特性进行研究,深入分析了大豆散体材料的动应力-应变关系、动弹性模量和阻尼比的变化规律,并对采用Hardin-Drnevich等效线性化黏弹性模型描述大豆散体材料动应力-应变关系的适用性进行了验证和讨论,为粮食仓储结构的动力分析和设计提供试验和理论参考。
1 试验概况
1.1 试样
样品为东北产大豆,含水率为9.0%,容重为696 g/L,密度为1.25 g/mL;大豆籽粒形状近似椭球形,随机选取50粒,利用游标卡尺测得其长轴平均为7.5 mm,短轴平均为 6.1 mm。参考土体动三轴试验方法制备大豆散体试样,如图1所示,试样尺寸均为直径61.8 mm,高度120 mm。

图1 大豆散体试样
1.2 试验方法
试验采用英国GDS单向激振动三轴试验仪,其测定动应变范围为0.01%~1.00%,压力室下方配有平衡锤,保证试验过程中围压稳定不变。研究了大豆散体试样在不同围压(σ3为50、100、150、200 kPa)下的动力特性。每个大豆试样的加载过程分为两步:等压固结和轴向动荷载施加。对每一个试样施加围压并保证大豆试样3个方向的主应力相等(σ1=σ2=σ3);围压施加完保持30 min,稳定后向试样施加等幅正弦波荷载,采用对同一试样逐级加大动应力的分级试验方法,振动频率为1 Hz。
图2为一个大豆散体试样在某一级动应力(σ)下振动50圈次的起始前3圈次和最后3圈次结果。由图2可以看出,在振动起始阶段大豆试样产生了微小的残余变形,随着振次的增加,残余变形逐渐减小,最后3圈次的滞回圈几乎完全重合。表1为一系列滞回圈的动力参数计算结果,由表1可知,第50圈次相对第3圈次动应变增大了1.4%,动弹性模量减小约0.7%,阻尼比减小约9.5%。除阻尼比减小相对较大外,动应变和动弹性模量相差很小。另外,每一级动荷载均通过增加振动圈次来消除残余变形的影响会引起孔压急剧上升,也会对试验结果造成影响。因此,采用每级动荷载振动3圈次的方法,试验中忽略残余变形对结果的影响。

图2 滞回圈对比

表1 计算数值
2 试验结果与分析
2.1 动应力-应变关系
大豆应变最大值与应力最大值并不同步,由于阻尼的影响,变形滞后于应力。大豆动应力-应变关系的滞回圈反映了大豆的黏性特性。Hardin-Drnevich模型(简称H-D模型)是一种等效线性化黏弹性模型,在描述土体等散体材料的动应力-动应变关系中具有广泛的应用[19]。H-D模型是采用双曲线来描述循环荷载作用下材料的骨干曲线,即
(1)
式中:σd为动应力幅值,kPa;εd为动应变幅值,%;a、b为参数。根据动三轴试验结果,将每级动荷载作用下滞回曲线的顶点相连得到大豆散料的骨干曲线,并采用式(1)对大豆的骨干曲线进行拟合,结果见图3。
从图3可以看到,H-D模型与试验值拟合较好,不同围压下大豆的骨干曲线H-D模型拟合参数如表2所示,拟合决定系数均达到0.88以上。不同围压下,大豆骨干曲线的变化规律基本相同,动应力幅值随动应变幅值的不断增大而增加,骨干曲线斜率不断减小,大豆散料的动应力-动应变关系具有明显的非线性特征。同时发现,随着围压的增大,大豆骨干曲线的斜率逐渐增大(拟合骨干曲线在动应变0.05%时,围压50、100、150、200 kPa对应的初始斜率分别为22.39、30.86、37.41、43.60),即相同动应力幅值对应的动应变幅值越来越小,表现出围压的强化作用。

图3 采用H-D模型拟合骨干曲线

表2 H-D模型拟合参数
2.2 动弹性模量
动弹性模量反映某一级动应力作用下,大豆散体试样的弹性变形特征。对于理想弹性体,动应力与动应变在时间上应同步对应。但从图2和图3可以看出,大豆散体试样并非理想弹性体,其动应力与相应动应变在时间上并不同步,而是动应变较动应力有一定的时间滞后。根据图2所示大豆散体的滞回曲线,定义此滞回环的平均斜率为动弹性模量Ed,即
(2)
基于H-D模型,由式(1)可得大豆动弹性模量与动应变幅值的关系表达式。
(3)
采用式(2)对动三轴试验结果进行计算,得到大豆动弹性模量随动应变的变化规律,并将式(2)和式(3)结果进行对比,结果如图4所示。由图4可以看出,基于H-D模型所建立的大豆动弹性模量随动应变幅值的预测模型与试验结果拟合较好,进一步反映H-D模型描述大豆动应力-动应变关系的合理性。大豆的动弹性模量随动应变幅值的增大呈逐渐减小的趋势;相同动应变幅值条件下,动弹性模量随围压增大而增大。围压为50 kPa时,动弹性模量随动应变幅值的增加呈显著的非线性减小的趋势。当围压超过100 kPa,动弹性模量在0.05%~0.25%的动应变范围有小幅的波动,总体呈现出先减小后增大的趋势,当动应变幅值大于0.25%又逐渐减小。这是由于围压增大,使得大豆试样更加致密,在加载初期表现出一定的强化现象,进而逐步趋于稳定;随着外荷载的逐渐增加,大豆颗粒间的联结遭到破坏,产生滑移和变形,动弹性模量逐渐减小。
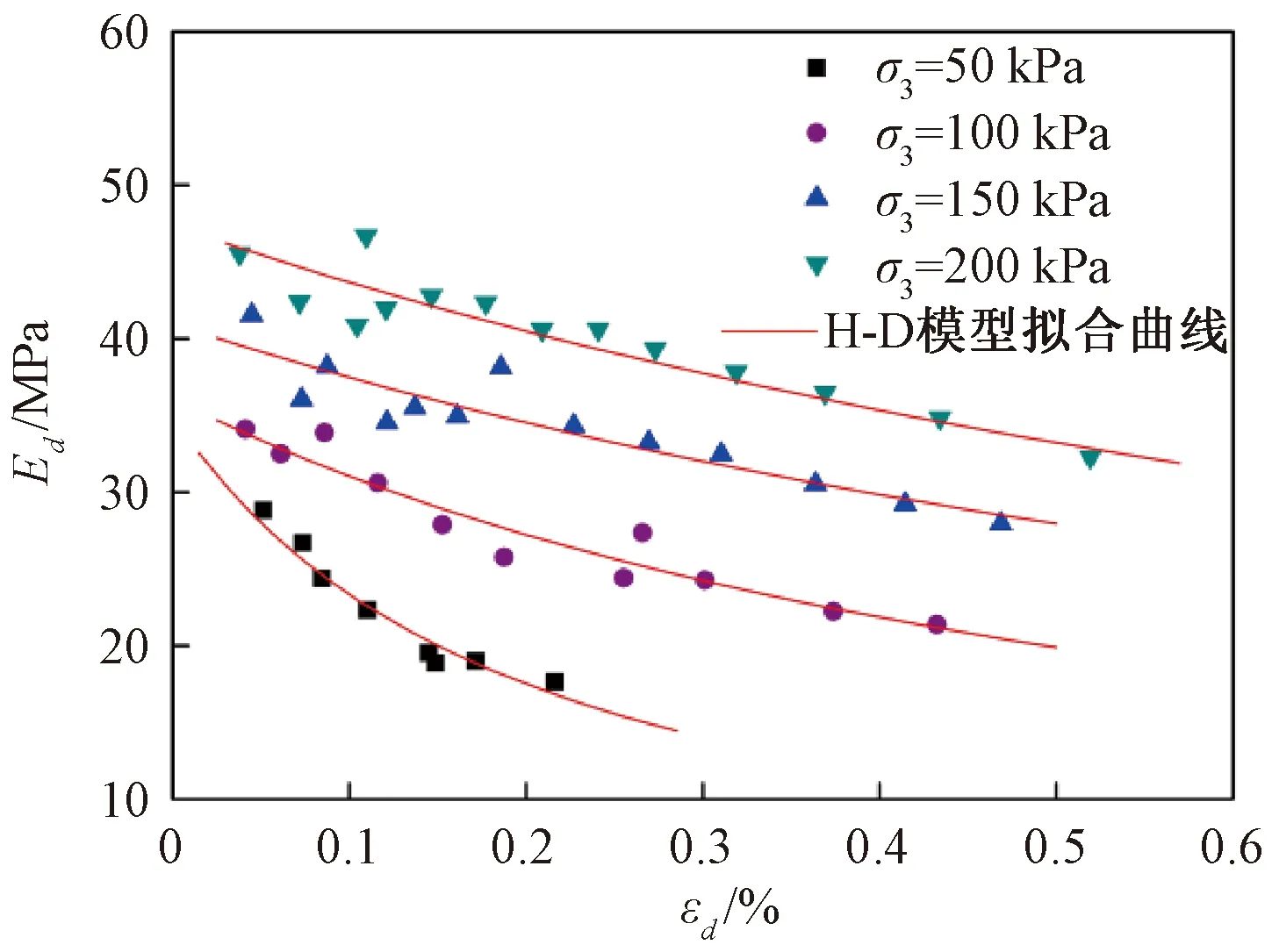
图4 不同围压下大豆动弹性模量随动应变幅值的变化关系
2.3 阻尼比
滞回曲线可以反映大豆散体试样的黏滞性,黏滞性越大,滞回环的形状就越趋于宽厚,反之则趋于扁薄。这种黏滞性实质上是一种阻尼作用,而阻尼比是衡量材料振动耗能能力的重要指标。一般地,阻尼作用可用等效滞回阻尼比(λ)来表征[20],其值可从滞回曲线求得。
(4)
式中:AL为滞回曲线所包围的面积(如图5所示),即一个周期内消耗的能量;AT为材料在一个循环荷载内的最大弹性应变能,即图5中阴影部分三角形所示的面积。
滞回曲线面积AL表示循环荷载下大豆的滞回耗能,AL越大,说明大豆耗散的能量越多,其振动耗能能力也越强。图6为不同围压下滞回曲线面积AL随动应变幅值的变化关系。由图6可以看出,不同围压下AL随动应变幅值的增加均呈现出非线性增大的趋势,即动荷载越大,大豆耗散的能量越多。同时,当动荷载较小(动应变幅值不超过0.3%)时,不同围压下滞回曲线面积AL非常接近,随着动荷载进一步增大,相同动应变值对应的滞回曲线面积AL随围压的增加明显增大,即围压越大,大豆散料的滞回耗能能力越强。
根据试验结果,通过式(4)计算得到不同围压下大豆阻尼比随动应变幅值的变化关系如图7所示。由图7可以看出,不同围压下大豆阻尼比介于5%~20%,且随动应变幅值的增加均呈增大的趋势;当动荷载较小时(动应变幅值<0.1%),不同围压下大豆阻尼比较接近,且数值波动剧烈,这是由于加载初期,大豆试样逐渐压密,在压密过程中产生不可忽略的残余变形,进而引起大豆的滞回耗能,阻尼比显著增大;随着动应变幅值的增加,大豆逐渐变得致密,储存的弹性应变能开始快速增长,阻尼比增速变缓;在加载后期,随着动应变幅值的增大,大豆颗粒间联结被破坏,不断产生新的滑移,内部损伤导致弹性性质不断弱化,进而滞回耗能逐渐增大,阻尼比也显著增大;同时不难看出,除加载初期(动应变幅值<0.1%),阻尼比数值波动比较剧烈外,相同动应变幅值对应的阻尼比均呈现出随着围压的增大而减小的趋势,这是由于围压越大,大豆试样越致密,其表现的弹性性质越明显。

图7 不同围压下阻尼比随动应变幅值的变化关系
3 结论
通过开展大豆散体材料的动三轴试验,研究了不同围压下大豆散体材料的动力特性。大豆的动应力-应变关系具有显著的非线性和滞后性特征,采用Hardin-Drnevich等效线性化黏弹性模型可以较好地模拟大豆散体材料的动应力-动应变关系。不同围压下,大豆骨干曲线的动应力幅值随动应变幅值的增大呈非线性增长的趋势,且围压越大,骨干曲线的斜率越大,表现出围压的强化作用。大豆的动弹性模量随动应变幅值的增大呈逐渐减小的趋势,相同动应变幅值条件下,动弹性模量随围压增大而增大;基于H-D模型所预测的动弹性模量可较好地描述大豆动弹性模量随动应变幅值的变化规律。滞回曲线面积随动应变幅值的增加呈现出非线性增大的趋势,围压越大,大豆的滞回耗能能力越强;不同围压下大豆阻尼比介于5%~20%,阻尼比随动应变幅值的增加呈增大的趋势,且相同动应变幅值对应的阻尼比随围压的增大而减小。

