信息技术支持真实情景中的数学建模教学——来自德国的经验

邵 铭 宇 苏 航

随着21世纪计算机与信息技术的高速发展，数学在社会各个领域的应用层次和应用范围也在不断深化和扩展，数学建模作为沟通数学与现实领域的桥梁，近年来成为各国课程的重要发展内容。关于数学建模的创新教学，国内有许多学者尝试提出解决方案，其中有很大一部分整合了信息技术或是真实的建模案例。比如谭玉华提倡真实世界中的数学建模教学，让学生考虑原始背景的天然复杂性；①谭玉华. 真实情境驱动的高中数学建模教学[D/OL]. 华东师范大学, 2004[2020–10–25]. https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CMFD&dbname=CMFD9904&filename=2004087948.nh&v=3qSfDUzZt9wYvyOXgG4N9ZRg88e8jSXks xKN9c9V0b63gQ0mECS8%25mmd2F%25mmd2FGhe%25mmd2BBAhZed.颜荣芳等人，朱维钧和罗娟各自提出了现代信息技术应用于数学建模教学的多种方式，包括利用数学软件包完成复杂的模型求解、评价和验证，利用网络和多媒体技术直观生动地展示问题背景信息、数学模型及其对参数变化的敏感性等；②颜荣芳, 张贵仓, 李永祥. 现代信息技术支持的数学建模创新教育[J]. 电化教育研究, 2009(03): 98–100.③朱维钧, 罗娟. 多媒体在数学建模教学中的应用[J]. 廊坊师范学院学报(自然科学版), 2010, 10(02): 126–128.蔡苏等人利用增强现实（AR）技术开发教学材料，把真实环境的影像和虚拟的AR对象（数学模型）叠加到同一画面，连通数学和现实世界，学习者还能对虚拟/现实对象进行操作并接收相应的视觉或数据反馈。④蔡苏, 张晗, 薛晓茹, 等. 增强现实 (AR) 在教学中的应用案例评述[J]. 中国电化教育, 2017(3): 1–9.而在国际上，引入真实世界的案例或整合信息技术也是数学建模创新教学中常见的做法。例如布拉克（Bracke）和盖革（Geiger）、凯瑟（Kaiser）和施瓦茨（Schwarz）都曾在学校教学实验中让学生解决源自真实世界的建模问题，包括德国高铁轨道的设计、指纹识别、世界杯期间的交通流量等；⑤BRACKE M, GEIGER A. Real-World Modelling in Regular Lessons: A Long-Term Experiment[C]//KAISER G, BLUM W,FERRI R B, et al. Trends in Teaching and Learning of Mathematical Modelling: ICTMA14. Dordrecht: Springer Netherlands,2011: 529–549.⑥KAISER G, SCHWARZ B. Authentic Modelling Problems in Mathematics Education−Examples and Experiences[J]. Journal Für Mathematik-Didaktik, 2010, 31(1): 51–76.内维斯（Neves）等人介绍了一个操作较为简单的计算机建模系统Modellus对学生数学建模活动的支持作用，该系统可以在交互式对象的动画和该对象的数学模型之间建立可视化的实时对应。⑦NEVES R G, SILVA J C, TEODORO V D. Improving Learning in Science and Mathematics with Exploratory and Interactive Computational Modelling[C]//KAISER G, BLUM W, FERRI R B, et al. Trends in Teaching and Learning of Mathematical Modelling: ICTMA14. Dordrecht: Springer Netherlands, 2011: 331–339.还有学者关注教学法的革新。如布鲁姆（Blum）和莱斯（Leiß）在大型项目DISUM中对比了两种数学建模教学模式：指令式和操作——策略性模式，发现后者能显著提升学生的建模表现。⑧BLUM W, LEISS D. How Do Students and Teachers Deal with Modelling Problems?[C]//HAINES C, GALBRAITH P, BLUM W, et al. Mathematical Modelling: Education, Engineering and Economics (ICTMA12). Chichester: Horwood Publishing, 2007:222–231.这里的操作策略性模式强调为学生提供个性化的即时干预，它们遵循“最小帮助原则”，尽可能保持学生的独立性。⑨ZECH F. Grundkurs Mathematikdidaktik: Theoretische und praktische Anleitungen für das Lehren und Lernen von Mathematik[M]. 8th ed. Weinheim: Beltz, 1996: 221.

上述种种方案虽然取得了一定的成效，但普遍没能在资源设计、教学方法、技术操作层面同时给与教师支持。提倡真实情景的方案或是给出一些理论化的原则，或是关注个别建模案例的实践，很少能给出可操作的、一般化的、关于真实世界数学建模任务的创设指南。引入信息技术或是新型教学方法的方案分别需要教师具有较高水平的软件操作技能、教学灵活性或是对学生困难具有准确的判断，由于缺少系统的教师专业培训，它们通常无法在日常教学中长期实行。而德国的数学城市地图项目（Math City Map-Project，简称MCM项目）提出以（移动）信息技术支持真实情景中的数学建模教学，同时提供通用型任务模板，搭建资源平台并组织教师培训，较好地弥补了前述项目的不足。该项目于2012年由法兰克福大学教授马蒂亚斯·路德维希（Matthias Ludwig）发起，至今已和德国、法国、意大利、西班牙等多个国家的中学合作开展教学实验，在欧洲数学教育社区形成了广泛影响。①参见项目门户网站https://mathcitymap.eu。鉴于此，本研究深入分析该项目的特色，总结其中的先进经验，取其精华去其糟粕，助力我国数学建模教学的创新改革。

一、理论框架和研究问题

数学建模在当今世界的各个领域有广泛的应用，关于其含义也有不同的界定。这一部分聚焦我国高中数学新课标中的数学建模，明确其内涵，梳理我国中学数学建模教与学的现状，本研究引出德国数学城市地图项目的借鉴价值，进而确定具体的研究问题。

（一）数学建模的过程定义和能力划分

关于数学建模的定义，社会各界一个普遍的共识是，数学建模连通了现实世界和抽象形式化的数学世界，是一种从现实世界到数学世界的映射求解过程。按照这一观点，数学建模过程包含典型的四个节点——情景问题、数学问题、数学结果和情景结果−和四个环节——表征、应用、解释和评价（PISA建模循环，见图1）。②OECD. PISA2012 assessment and analytical framework: Mathematics, reading, science, problem solving and financial literacy[M]. Paris: OECD Publishing, 2013: 26.而布鲁姆（Blum）等人认为在情景问题和数学问题之间还存在一个关键的中间状态——现实模型，并且更进一步地，把客观存在的现实问题情景和人们主观上对这一问题情景的理解（情景模型）看作两个节点，经过几次修订，最终形成当今国际上流传较广的七环节建模过程框架（见图2）。①BLUM W, LEISS D. How Do Students and Teachers Deal with Modelling Problems?[C]//HAINES C, GALBRAITH P, BLUM W, et al. Mathematical Modelling: Education, Engineering and Economics (ICTMA12). Chichester: Horwood Publishing, 2007:222–231.对比四环节和七环节建模过程框架，不难发现后者是前者的扩展和精细化版本，将七环节框架中的部分环节进行合并和概括，就得到四环节框架。

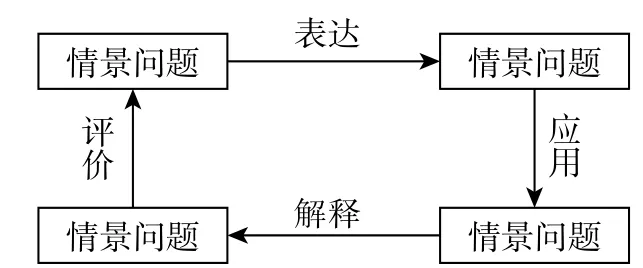
图1 PISA四环节建模循环

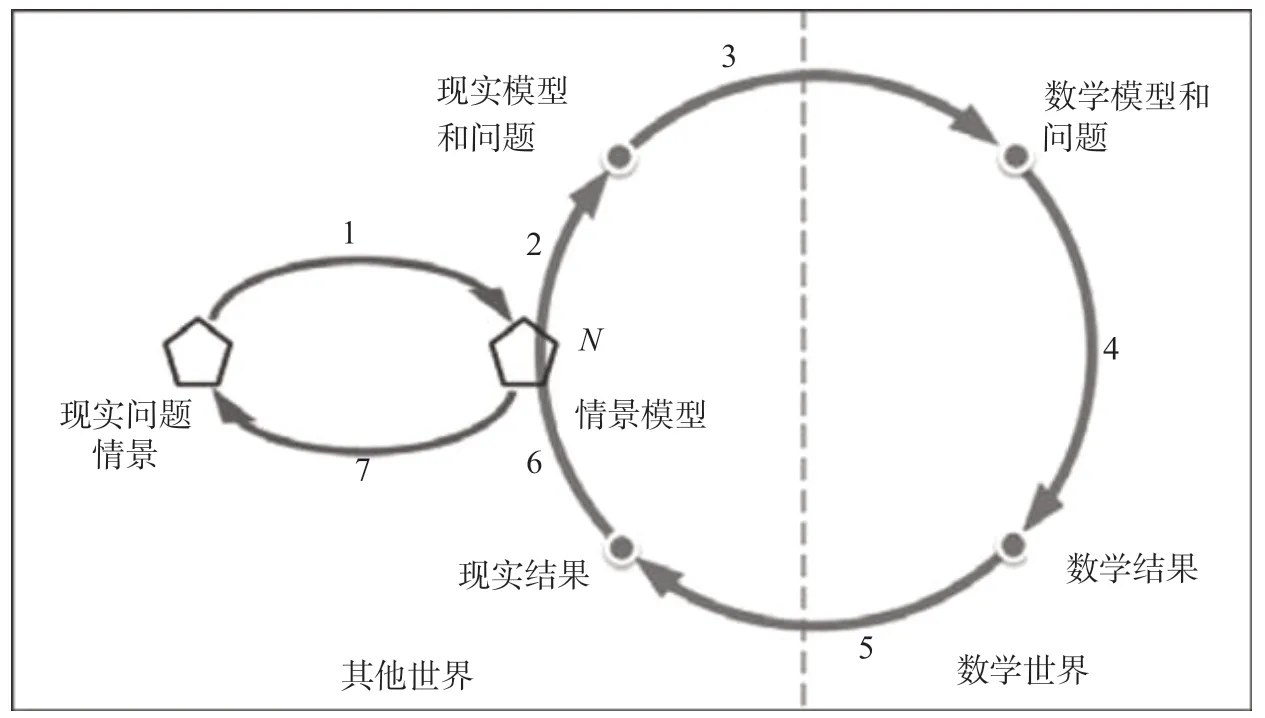
图2 布鲁姆七环节建模过程框架

由于布鲁姆的七环节建模框架涵盖的建模环节最多，以此为代表，本研究对这七个环节的内容进行简要介绍。如图2所示，环节1：理解问题，构造情景模型来描述现实问题情景。环节2：进一步简化和结构化情景模型，提炼出现实模型和相关目标。环节3：数学化——把现实的模型和问题翻译为数学模型和数学问题，识别重要变量和关系。环节4：模型求解——用数学方法解决所提出的数学问题，获得数学解答。环节5：解释数学结果——根据具体的现实情景解读数学结果，获得现实结果。环节6：评价和反思——评价现实结果的有效性，讨论模型中假设的合理性，分析和比较不同的模型。环节7：在现实问题情景中解读现实结果。费里（Ferri）指出，学习者不一定连续地遍历上述所有环节，而是有可能直接从现实问题情景跳跃到数学模型，或是在两个世界之间反复跳转。②FERRI R B. Theoretical and Empirical Differentiations of Phases in the Modelling Process[J]. ZDM, 2006, 38(2): 86–95.21世纪以来，我国数学课程中对数学建模的描述也紧跟国际脚步，从不完备的四环节逐步发展为七环节。最新颁布的《普通高中数学课程标准（2017年版）》（以下简称新课标）指出数学建模过程主要包括“实际情境中从数学的视角发现问题、提出问题，分析问题、建立模型，确定参数、计算求解，检验结果、改进模型，最终解决实际问题”，与上述七个环节基本一致。③黄健, 鲁小莉, 王鸯雨, 等. 20世纪以来中国数学课程标准中数学建模内涵的发展[J]. 数学教育学报, 2019, 28(03): 18-23+41.

在界定数学建模过程的同时，许多学者都尝试对数学建模能力进行划分。这些研究按照宏观和微观视角可以分为两类。微观视角下的数学建模能力是按照数学建模过程中的各个环节划分出若干“子能力”。这一做法在西方学者凯瑟（Kaiser），马斯（Maaß），布洛姆霍伊（Blomhøj）和詹森（Jensen）等人的研究中较为常见。①KAISER G. Modelling and Modelling Competencies in School[C]//HAINES C, GALBRAITH P, BLUM W, et al. Mathematical Modelling: Education, Engineering and Economics(ICTMA12). Chichester: Horwood Publishing, 2007: 110–119.②MAASS K. What Are Modelling Competencies?[J]. ZDM, 2006, 38(2): 113–142.③BLOMHØJ M, JENSEN T H. Developing mathematical modelling competence: Conceptual clarification and educational planning[J]. Teaching mathematics and its applications, 2003, 22(3): 123–139.对应布鲁姆七环节建模框架，即有理解现实问题情景、提炼现实模型、数学化、模型求解、解释数学结果、结果评价和模型反思、解读现实结果等子能力。④BLUM W. Can Modelling Be Taught and Learnt? Some Answers from Empirical Research[C]//KAISER G, BLUM W, FERRI R B,et al. Trends in Teaching and Learning of Mathematical Modelling: ICTMA14. Dordrecht: Springer Netherlands, 2011: 15–30.微观视角下的另一类研究是对数学建模“能力水平”的划分，这些研究同样是基于建模过程框架，认为学生每往前推进一个环节，即代表一次认知障碍的突破，其建模能力的水平就越高。例如徐斌艳和路德维希 （Ludwig）根据七环节建模过程框架划分出六个能力水平：水平0代表学生无法理解具体的现实情景，不能识别出任何问题；水平1代表学生能够理解现实情景并将其结构化，但是无法找到与数学相关的线索……以此类推。⑤徐斌艳, LUDWIG M. 中学生数学建模能力水平的实验分析[J]. 中学数学月刊, 2007(11): 1-2+30.这一水平划分的方式也被国内外的一些学者所沿用。⑥孙翔宇. 上海市高中生数学建模能力的调查与分析[J]. 教育测量与评价, 2016(06): 44–49.⑦MEHRAEIN S, GATABI A R. Gender and Mathematical Modelling Competency: Primary Students’ Performance and Their Attitude[J]. Procedia - Social and Behavioral Sciences, 2014, 128: 198–203.

宏观的视角下的建模能力研究将数学建模的整个过程纳入考虑，根据问题情景的复杂度和学生实现的数学化的复杂程度，划分出若干“能力水平”。比较典型的有PISA 2012中的四个水平——水平I：问题情景是纯数学的，学生直接处理数学问题而不需要进行数学化。水平II：从非数学情景中建立数学模型，模型需要的假设、变量、关系和约束条件已经给出；通过给定的模型和数学结果，直接给情景下结论。水平III：模型所需的假设、变量、关系和约束条件能从题目中找到；修改一个给定的模型以适应条件的改变；结合问题情景解读一个模型或者数学结果。水平IV：模型所需的假设、变量、关系和约束条件需要定义；评价和反思与问题情景有关的模型；联系或比较不同的模型。⑧TURNER R, BLUM W, NISS M. Using competencies to explain mathematical item demand: A work in progress[M]//STACEY K, TURNER R. Assessing mathematical literacy. Springer, 2015: 85–115.我国的新课标在划分学生的数学建模素养水平时也采取了同样的方式，但删除了纯数学情景所对应的水平。⑨中华人民共和国教育部. 普通高中数学课程标准(2017年版)[M]. 北 京: 人民教育出版社, 2018.类似的划分方式也见于朱娅梅，西列尔（Siller）等人的研究中。⑩朱娅梅. 我国八年级学生数学建模能力的调查研究[J]. 上海教育科研, 2017(04): 51–54.⑪SILLER H-S, BRUDER R, HASCHER T, et al. Competency level modelling for school leaving examination[C]//KRAINER K,VONDROVA, N. Proceedings of CERME9. Prague: Charles University in Prague, Faculty of Education and ERME, 2015:2716-2723.

对比微观和宏观视角下的数学建模“能力水平”研究，前者多根据学生在某个特定问题中完成的建模环节来判定学生的水平，却没有考虑问题本身的特性，因而具有一定的局限性。一个在复杂问题情景中只达到水平2的学生，其建模能力未必不如在简单情景中达到水平5的学生。而宏观视角下的研究综合考虑了建模问题本身的难度（问题情景的复杂度和需要数学化的程度）和学生在不同难度的建模问题中的表现，对学生的水平进行了较为可靠的区分。综上，本研究认为数学建模的“能力水平”更适合采用宏观的视角（如PISA四水平模型）来划分，数学建模的各项“子能力”更适合以微观视角（即各种过程框架）来区分。

（二）我国中学数学建模的学习困难和教学挑战

我国新课标将“数学建模”列为核心素养和高中课程内容主线之一，强调了发展学生数学建模能力的重要性。但若干实证调查表明，我国中学的数学建模教育任重道远。这些研究中，有不少是基于微观视角和七环节建模过程框架，划分出若干数学建模的“能力水平”或“子能力”，调查对象涉及上海、长沙、大同、西安、郑州等不同地区的初高中生，用于测试的建模问题多为“菠萝削皮”“足球缝制”“粉笔设计”等贴近现实的复杂问题。结果显示：学生提炼现实模型和数学化的子能力（对应七环节建模框架的环节2－3）普遍较弱。彭墨缘还发现，学生在建模完成后很少能考虑其他可能的模型假设，也即学生对模型的反思能力（环节6）较差。①孙翔宇. 上海市高中生数学建模能力的调查与分析[J]. 教育测量与评价, 2016(06): 44–49.②彭墨缘. 高中生数学建模能力性别差异研究[D/OL]. 华东师范大学, 2017[2020–10–31]. https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CMFD&dbname=CMFD201801&filename=1017073315.nh&v=UD%25mmd2BQuNHDQSTSJaCb1 LG6pPbIenjmVv0BM3ucc4Hebarl5b3l2isD9bxxnWdTh7K0.③徐斌艳, 沈丹. 我国学生的数学建模能力水平分析−−以6~9年级学生的“缝制足球”实验为例[J]. 中学数学月刊,2014(07): 37–40.另一些研究采用宏观的视角和PISA2012的水平模型，发现学生在再现层次的数学建模问题（水平I－II）中完成度较高，能熟练识别常见的标准模型，但在联系和反思层次的问题上（水平III－IV）表现不佳，多数停留在了将现实情景转化为数学模型的步骤上。④朱娅梅. 我国八年级学生数学建模能力的调查研究[J]. 上海教育科研, 2017(04): 51–54.综上，可以认为我国中学生在较为复杂的现实问题情景中难以提炼现实模型和数学模型，模型反思能力较差。

徐斌艳认为出现上述学习困难的一个原因是学校的数学教学长期专注于知识本身，孤立于具体的现实情景，学生很少有机会直接体验数学在解决实际问题中的价值和作用。⑤徐斌艳, LUDWIG M. 中学生数学建模能力水平的实验分析[J]. 中学数学月刊, 2007(11): 1-2+30.牛伟强指出，缺少源于真实情景的、适合初高中生水平的建模任务资源，是影响中学数学建模教育的核心因素。⑥牛伟强. 高中生数学建模能力发展研究[D/OL]. 华东师范大学, 2019[2020–10–30]. https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CDFD&dbname=CDFDLAST2019&filename=1019835657.nh&v=hQjzVvgoQJJyWIL3eAft9BFB2xqdZqlNvAp xEi9mL8Yt6N%25mmd2B2AeYfwvVVZ4Wk2YHg.李明振和喻平还发现，许多中学教师对数学建模教育态度消极，缺乏建模活动经历和教学经验，也是数学建模课程实施效果不佳的原因之一。①李明振, 喻平. 高中数学建模课程实施的背景、问题与对策[J]. 数学通报, 2008, 47(11): 8-10+14.

（三）德国MCM项目的理论基础和参考价值

针对上述问题，国内学者曾提出若干数学建模教学的改进建议。但正如前文所言，这些建议或是停留在理论层面，或是只关注教学实践中的一个方面。而成功的教学创新改革需要有效的技术与课程整合模式，软硬件的合理安排，教师培训，辅助资源的创设等一系列配套的支援计划。②黄利发. 信息技术与课程整合中全面的教师培训、巩固与支援计划[J]. 现代教育技术, 2011, 21(05): 43–47.德国MCM项目基本具备了这些要素，借助（移动）信息技术支持教师在户外真实情景中的数学建模教学，培养学生在布鲁姆建模框架中的子能力，这对于破解我国数学建模教与学的困局而言，不失为一个可以借鉴的范本。

德国MCM项目的理论基础主要有三。其一是数学游踪（Math Trail），这一概念是由澳大利亚学者布莱恩（Blane）和克拉克（Clark）首先提出的，指一系列真实地点串联起来的路线，每个地点都对应一个数学任务，与所在地的现实情景或现实对象相连接。③BLANE D C, CLARKE D. A. Mathematics trail around the city of Melbourne[J]. Monash Mathematics Education Centre in Monash University, 1984: 169–181.它可以调动学习者的知觉运动系统，让他们在一个相对轻松的协作环境中运用数学知识解决现实世界中的问题、锻炼数学建模能力。④SHOAF M, POLLAK H, SCHNEIDER J. Math Trails[M]. Bedford: COMAP, 2004: 8-10.其二是布鲁姆七环节建模框架。其三是分级提示（Stepped Hints），指在学生解决问题的过程中，根据学生的困难和需要逐步呈现相应提示的系统，它让学生尽可能依赖自己的知识和经验自主完成任务，进而能够促进学生的自主学习。⑤FRANKE-BRAUN G, SCHMIDT-WEIGAND F, STÄUDEL L, et al. Aufgaben mit gestuften Lernhilfen - ein besonderes Aufgabenformat zur kognitiven Aktivierung der Schülerinnen und Schüler und zur Intensivierung der sachbezogenen Kommunikation[M]//Kasseler Forschergruppe. Lernumgebungen auf dem Prüfstand: Zwischenergebnisse aus den Forschungsprojekten. Kassel: Kassel University Press, 2008: 27–42.基于这些理论和概念，MCM项目团队开发移动应用程序，将构成数学游踪的户外建模任务（简称MCM任务）呈现在地图上，每个任务还配有相应的分级提示和答案验证系统；同时搭建门户网站，以便于教师自主设计MCM任务（包括相关的分级提示和答案）。在这两个产品的帮助下，教师便可以很容易地将学生组织到不同的任务地点，让学生在自主建模的过程中发展布鲁姆建模框架中的子能力。⑥LUDWIG M, JABLONSKI S. Doing Math Modelling Outdoors-A Special Math Class Activity designed with MathCityMap[C]//DOMENECH J, MERELLO P, DE LA POZA E, et al. 5th International Conference on Higher Education Advances (HEAd’19). València: Editorial Universitat Politècnica de València, 2019: 901–909.本研究把这一教学模式称作MCM教学。以此为核心，项目进一步提供通用型任务指导教师的资源设计，利用门户网站搭建资源平台，并在整个欧洲范围内培训职前/在职教师，为教师提供了系统而全面的支持。⑦参见网站http://momatre.eu/.

基于上述讨论，本研究首先对项目内容进行介绍，之后聚焦学生数学建模能力的发展，通用型任务的设计，门户网站的建设，教师培训四个方面，对项目的特色进行深入分析，在此基础上，总结项目有哪些先进经验和不足之处，为信息时代下我国数学建模教学的创新改革提供有意义的参考。

二、MCM项目的主要内容

（一）移动应用程序

MCM项目的移动端应用程序Math City Map（简称MCM－App）整合了移动网络、数字地图和GPS定位技术，用于显示数学游踪、游踪内的MCM任务及其位置，帮助用户导航到任务所在地点并解决任务，主要服务于学习者。学生在MCM－App中输入某数学游踪的名称或编号，即可看到该游踪内的所有MCM任务及其位置分布，如图3.1 所示。点击游踪内的一个任务（图3.2），可以看到任务内容（图3.3）。这些任务需要学生亲自到达指定地点、现场收集相关数据后才能解决。在尝试解决任务的过程中，学生还可以根据需要查看分级提示（图3.4），或是直接输入答案（图3.5）并查看答案反馈 （图3.6）。成功作答后，学生可以选择查看“参考解答”，或是跳转到游踪内的“下一任务” （图3.6）。MCM-App适用于安卓、IOS等移动操作系统，App内的所有数据都可以离线使用。

图3 MCM–App的用户操作界面

（二）门户网站

为了方便在MCM－App中投放任务，MCM项目团队搭建门户网站www.mathcitymap.eu，供用户（主要为教学者）在后台创建、分享MCM任务和数学游踪，创建完成后，这些任务和游踪就可以在App内显示。用户只需通过简单的注册，进入入口（Portal）界面，就可以看到一个虚拟地图和若干功能模块，如图4所示，点击“游踪（Trails）”或 “任务（Tasks）”模块并在搜索栏输入某一地点，就可以快速看到该地点附近公开的数学游踪或MCM任务，或是创建自己的对应项目。图5显示了网站的任务创建表单和某个具体的任务案例，其中包括了需要在MCM－App中显示的任务要素以及其他背景信息。这些信息可以由用户独立创建，或是在“复制”“粘贴”他人任务的基础上予以改编。同样，用户也可以选择“公开”自己任务的获取权限。而在游踪创建页面，用户选择某一区域内的若干任务（自己或他人的），将其按顺序添加到某个自定义菜单内，即可生成一个数学游踪（见图6）。针对每一段数学游踪，网站会自动提供一份PDF的配套手册，包含游踪标题页、游踪地图、游踪内所有任务的内容和图片，以便于教师打印，让学生在户外即使没有手机也可以通过纸笔经历数学游踪。

图4 www.mathcitymap.eu的英文版入口界面

图5 www.mathcitymap.eu中的任务创建示例（部分文本由英文翻译成中文）

图6 数学游踪创建页面（部分文本由英文翻译成中文）

（三）通用型任务

由上文可知，要创建一个MCM户外建模任务，用户需要提供包括任务内容、分级提示、参考解答、所需工具在内的多种信息，所涉及的现实对象通常是楼梯、坡道、建筑物、水池、交通工具等常见的物体。考虑到关于同一类现实对象，对应的数学建模任务，解答和提示大多类似，为了帮助世界各地的教学者根据在地的现实情景不断创设新的户外数学建模任务，节约教学资源的准备时间，MCM的项目团队在众多任务案例和实践经验的基础上，总结出一系列通用型任务（Generic Tasks）。其中每个任务都针对一类特定现实对象，给出任务主题和要求、需要测量的数据、参考解答、可能的提示和可能的应用场景。这些任务均可以在网上下载。①通用型任务网址为http://momatre.eu/the-project/generic-tasks/.下文展示了一个立体几何通用型任务。

任务主题：计算某一圆台形物体的体积/质量。

适用的现实情景和对象：雕塑、路障、花盆，等等。

需要收集数据：

物体的底面圆和上表面圆的直径/半径，物体的高（上下底面圆心之间的距离），物体侧面的母线长。

参考解答：

如上图所示，圆台的体积可以按照如下公式计算：

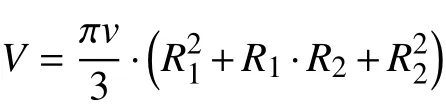
其中圆台的高v可以利用毕氏定理，用上下底面的半径R1、R2和母线s表示出来。

可能的提示：

（1）观察花盆的形状，你会联想到哪个几何体？

（2）如果你不知道圆台的体积公式，你可以利用其他几何体来近似花盆的形状。

（3）你可以用某种方法找到花盆的平均底面半径，进而利用圆柱的体积公式。

（4）你可以测量花盆的高吗？

（5）花盆的高可以利用毕氏定理计算。

（6）注意单位换算。

（四）MoMaTrE教师培训

2017年，数学城市地图项目得到欧盟Erasmus+基金的支持，发起MoMaTrE（Mobile Math Trails in Europe）项目，在整个欧洲范围内培训数学教育专业的在校生（包括职前教师、在职教师、一般的数学教育研究者和数学建模爱好者），致力于普及项目的内容和理念，强化教学者关于MCM教学的经验和信心。①JABLONSKI S, LUDWIG M. Development of an Intensive Study Programme on Outdoor Mathematics Teaching with Digital Tools[C]//LUDWIG M, JABLONSKI S, CALDEIRA A, et al. Research on Outdoor STEM Education in the digiTal Age:Proceedings of the ROSETA Online Conference. Münster: WTM, 2020: 111–118.

以2019年3月18－30日的培训为例，该培训首先设置了若干专家讲座，讲座内容涉及MCM项目的理论背景，任务分析方法和各类相关技术（移动应用程序、门户网站、增强现实、游戏化）。从第二天开始，培训就穿插若干小组协作式的户外活动：学员首先以学生的视角亲身体验不同工具支持下的数学游踪（只有纸笔的数学游踪或同时使用MCM－App的数学游踪）；之后再以教学者的视角实地考查当地社区，设计初步的户外数学建模任务和游踪，并通过组内交流、专家反馈、组间审阅等活动，对任务进行反复修订，逐步领会MCM任务的设计原则；培训还会组织学员参观数学博物馆和当地学校，为其设计任务提供灵感来源。在初步确定数学游踪和游踪内的MCM任务后，每个小组将它们上传到门户网站上，使得游踪可以显示在MCM－App中。接下来利用该游踪进行教学实验，MCM团队联系若干当地中学，让中学教师引导学生运用MCM－App完成学员设计的数学游踪；与此同时，参训学员需要对中学生进行跟踪观察，主要考查学生是否按预期的方式完成游踪内的任务，并机动地对学生进行干预。根据观察收集到的数据，学员将再次对这些任务进行修订和完善，确定最终的数学游踪。②同本页①。

三、MCM项目的特色分析

这一部分结合项目内容，分析MCM项目的特色和优缺点。具体包括MCM教学模式对学生数学建模能力的促进作用，通用型任务的特点，门户网站（资源平台）的功能设置和教师培训的议程安排四个小节。

（一）MCM教学模式对数学建模能力的促进作用

在MCM教学模式中，MCM任务具有核心地位，学生的学习主要是通过在户外解决MCM任务而实现的。在这一节中，笔者结合具体的MCM任务案例，从微观和宏观两个视角分析MCM教学模式对学生数学建模能力的促进作用。微观视角下，选择项目本身的理论框架之一——布鲁姆七环节建模框架，分析学生在哪些建模环节的“子能力”能够得到发展；宏观视角则是微观视角的补充，以PISA 2012的四水平模型为框架，分析学生的建模能力可以发展到哪一“水平”。

1. 基于数学建模“子能力”的微观分析

图7显示了呈现在MCM－App中的一个关于花盆的建模任务和其中的3个提示，该任务由上文中的通用型任务改编而来，主要面向初中生。提示1和2都试图引导学生调动自己的先验知识，根据花盆的形状结构在记忆中搜寻相似的几何体（数学模型）。提示2在提示1的基础上给出一种模型替代策略，假设学生无法利用圆台模型继续求解，则可以考虑用已经学过的几何体来模拟花盆形状，代入熟悉的体积公式。这两个提示都可以推动学生从现实问题情景中提炼现实模型进而建立数学模型，对应布鲁姆七环节建模框架的环节2和3。如果学生仍然感到困难，他们可以继续查看第3个提示，该提示直接点明用于替代圆台体的几何模型——圆柱体，并提示学生寻找相关策略来确定模型中的关键变量——花盆平均底面半径的计算方式，引导学生完成布鲁姆框架中的环节3。

图7 MCM－App中的一个任务和相关分级提示（部分文本由德文翻译成中文）

MCM团队的一项调查显示，德国九年级的学生在实际解决该任务的过程中，共使用了三种不同的解法：解法一使用了圆柱模型，同时把花盆上下底面半径的平均值作为平均底面半径；解法二也使用了圆柱模型，但没有直接计算平均底面半径，而是分别以花盆的上下底面作为一大一小两个圆柱的底面，分别计算它们的体积再求得平均值；解法三直接使用圆台模型。三种解法在学生中出现的比例分别为60%，10%和10%，只有20%的学生没能建立合适的数学模型。①LUDWIG M, JABLONSKI S. Doing Math Modelling Outdoors-A Special Math Class Activity designed with MathCityMap[C]//DOMENECH J, MERELLO P, DE LA POZA E, et al. 5th International Conference on Higher Education Advances (HEAd’19). València: Editorial Universitat Politècnica de València, 2019: 901–909.值得注意的是，三种建模方案得到结果非常相似−79.563、78、78（单位：升），这主要是因为花盆的上下口径实际相差不大，即使用圆柱体来近似也不会由太大误差。任务的设计者在这里把“正确答案”设置成区间的形式 （74－82），使得在该区间内的结果都可以得到正向反馈，鼓励学生探索多样化的模型和解决方案。

在上述过程中，MCM－App中的分级提示系统和答案验证功能发挥了重要作用。德国学者泽赫（Zech）针对教师如何支持学生自主开展数学建模活动，提出了五步骤干预教学法。这些步骤遵循“最小帮助”原则，主张教师一次只给一种干预，从一般的情感鼓励、肯定学生结果、策略性提示、内容−策略性提示到内容性提示，循序渐进，当学生实在无法推进到下一步时再逐步给出之后的干预，让他们尽量依赖自身已有的知识和经验解题。②ZECH F. Grundkurs Mathematikdidaktik: Theoretische und praktische Anleitungen für das Lehren und Lernen von Mathematik[M]. 8th ed. Weinheim: Beltz, 1996: 221.这与分级提示能够支持学生自主学习的原理是一致的。可以看出，上面的3个提示也基本遵循“最小帮助原则”，它们分担了大部分的教师干预工作，而且提示2和3分别为策略性提示和内容−策略性提示。事实上，MCM（通用型）任务的提示大多具有类似的特性。通过在MCM－App中依次呈现这些提示和答案反馈，项目得以为学生创造一个自主学习的环境，提升他们在布鲁姆七环节建模框架下2－3环节中的表现——也即提炼现实模型和数学化的子能力，这是项目的优势之一。

2. 基于数学建模能力“水平”的宏观分析

在PISA2012的四水平模型中，学生的建模能力水平实际上是按照他们能够完成的建模任务的复杂水平划分的。以同样的花盆任务为例，该任务是在真实情景而非数学情景中给出的，花盆的形状是初中生并不熟悉的圆台体，建立几何模型所需的假设、变量、关系等都需要学生自己定义，因此任务已经达到了水平IV；而随着学生越来越多地查看提示，部分模型假设（把花盆近似看作圆柱体）和变量（花盆的平均底面半径）逐渐明晰，此时任务又退回到水平III。MCM项目中的许多建模任务都属于类似的情形，图5中的太阳能路灯任务就是另一个例子；而在另一些任务中（比如花盆的形状直接是圆柱体），问题情景较为简单，模型假设、各变量间的关系都十分明显，学生可以直接应用标准模型求解而不需要再作适应性的调整，这些任务属于水平II。综上，可以认为MCM教学模式能够推动学生的数学建模能力朝着水平II、III乃至水平IV发展。但它不一定能让学生完全达到水平IV，因为MCM任务并不注重学生对模型的反思（水平IV的能力要求之一），大多数学生在App中成功验证答案后便可以前往下一任务点，而不会考虑模型中假设的合理性或是其他可能的模型，这也是MCM项目的一个缺陷。

（二）通用型任务的特点分析

由上一小节可知，MCM任务的质量决定了MCM教学活动的质量。项目团队提供的通用型任务列表，实际上相当于一份一般化的、可操作的MCM任务设计指南。教师结合自身所处的现实环境，对通用型任务中的某些元素进行替换，就可以快速开发出一个在地化的、适用于MCM教学的新任务。因而通用型任务的质量会在很大程度上影响教师设计的MCM任务的质量。这一节尝试对项目给出的25个通用型任务的质量进行分析，一方面关注任务的内容设置，另一方面关注任务中分级提示的特性和排布方式，在此基础上评估通用型任务对教师的参考价值。

1. 任务内容普遍具有明确性、在场性、现实性，多数具有开放性

项目团队成员雅布伦斯基（Jablonski）等人曾提出高质量MCM任务内容的五个标准。明确性：任务涉及的现实对象在周围的环境中是唯一明确的。在场性：任务只能在现场完成，比如相关数据只能在现场测得。数学活动性：任务能够促使学生充分、灵活地运用多种数学知识和技能。开放性：任务可以有多种解法，可能涉及不同的数学模型、知识和数据收集策略。现实性：任务具有现实意义，其结果可以指导人们的生活实践。①JABLONSKI S, LUDWIG M, ZENDER J. Task quality vs. task quantity. A dialog-based review system to ensure a certain quality of tasks the MathCityMap web community[C]//WEIGAND H-G, CLARK-WILSON A, DONEVSKA-TODOROVA A,et al. Proceedings of the 5th ERME Topic Conference (MEDA). Copenhagen: University of Copenhagen, 2018: 115-122.以此为框架，本研究统计分别满足上述特性的通用型任务数量（见图8）。

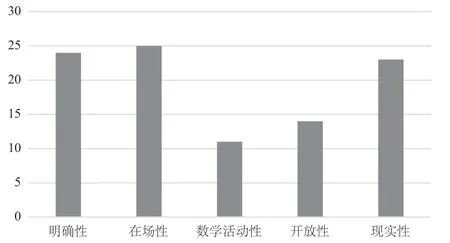
图8 满足各项标准的通用型任务数量分布

由图8可知，25个通用型任务中，有90%的任务都满足明确性、在场性和现实性，有接近60%的（14个）任务满足开放性。可以说，这些任务大多能够让学生在真实情景中开展数学建模活动，并鼓励学生探索多样化的模型和解题方案，进而强化学生的数学应用意识，保护他们的主观能动性和创新精神，给教师提供了较好的示范。与此同时，通用型任务在数学活动性方面表现较差，难以为教师提供参考，只有不到一半（11个）的任务具有较高的数学活动性，其余任务都只需要简单应用公式定理即可解决，这可能难以深化学生对数学概念和思想方法的理解。教师在设计任务内容的时候，仍然需要在数学活动性方面多加注意。

2. 任务提示遵循“最小帮助”原则，具有启发性和渐进性

上文提到，任务自带的分级提示若是遵循“最小帮助”原则，则可以有效支持学生的自主学习。泽赫提出了“最小帮助”原则下教师可以采取的五种干预策略，其中的策略性提示、内容−策略性提示和内容性提示同样可以作为MCM任务的分级提示而存在。考虑到MCM任务中可能还包含其他类型的提示，笔者另外引入弗雷德里希（Friedrich）和曼德尔（Mandl）所提出的三种任务提示——重述问题、聚焦关键信息和激活先验知识，①FRIEDRICH H F, MANDL H. Lern-und Denkstrategien-ein Problemaufriß[J]. Lern-und Denkstrategien. Analyse und Intervention, 1992: 3–54.作为前三种提示的补充，对25个通用型任务的110个提示进行分类。之后统计各类提示的数量，计算它们在单个任务中的平均数量和比例，得到图9。

图9 单个通用型任务中各类提示数量（平均值）的占比

由图9可知，通用型任务给出的提示多样，“策略性提示”和“策略−内容性提示”占据了绝大多数（合计81.82%），其次是“聚焦关键信息”和“激活先验知识”的提示，而“内容性提示”和“重述问题”的提示占比相对较低。关于它们在通用型任务中出现的顺序，“重述问题”“聚焦关键信息”和“激活先验知识”的提示通常在一开始就出现，这些提示只是将任务内本身的一些关键要素凸显出来，以调动学生先前的知识和经验。学生如果仍然感到困难，可以继续查看在后续给出的“策略性提示”或“策略−内容性提示”，而“内容性提示”一般在最后给出，直接点明相关模型或知识（如公式、定理等）的具体内容。由此可见，通用型任务的提示大体遵循“最小帮助”原则循序渐进，让学生尽可能自主解决问题。同时，较多的“策略性提示”和“策略−内容性提示”可以有效支持学生从现实问题情景中提炼现实模型和数学模型的过程。这些都是教师在设计任务提示的过程中可以借鉴的。

（三）门户网站的功能设置：促进资源交流和共建

这一节讨论MCM门户网站www.mathcitymap.eu的功能设置。起初，项目团队设立该网站，是为了让MCM任务的创建简单化、程式化。教师通过填写网页表单，即可创建一个MCM任务并把它同步到App中，从而避免了对App的程序脚本进行直接编辑。之后，项目团队又在任务创建页面添加了“公开”的选项，让创建者自主选择是否开放自己任务的存取权限，供其他用户“复制”，“粘贴”和再加工。同时，在数学游踪的创建页面，用户也可以直接将他人的任务添加到自己的游踪菜单内。这就极大地激发了网站在线社群的活力，使得世界各地的注册用户都能参与到MCM教学资源的交流和共同建设中来。李江和夏泽胜曾指出，以学习者为中心的资源供给和以自发式为主导的资源建设共同体是“互联网+”时代教师支持的重要方面。①李江, 夏泽胜. “互联网+”时代的教师培训:模式更新、价值证成与行动路径[J]. 教师教育研究, 2020, 32(04): 38–44.正是通过上述与资源分享、引用和改编有关的功能，MCM的门户网站才得以集思广益，打造了一个多文化背景的、开放式的、以用户为中心的资源共建平台，项目团队还会定期在网站评选 “每周任务”和“每月游踪”，作为优秀案例供教师参考，为教师的资源准备工作提供了有效的支持。

（四）教师培训倡导“做中学”，促进交流与反思

任何新的教育技术和理念，要想在中学校园得以推广，都离不开一线教师的认同、参与和实践，而教师培训是获得教师认同，推动教师参与实践的重要途经。分析数MCM的教师培训子项目MoMaTrE，发现它主要有以下几点特色值得借鉴。

1. 设置“教师/学生”双重视角，倡导“做中学”

回看MoMaTrE培训的议程设置，不难发现它一直注重学员对MCM教学活动全方位、多角度的体验。这主要是由于项目团队发现：缺乏教学活动经验、感到难以创建MCM任务和游踪是阻碍教师积极参与教学实践的两大原因。培训在几次理论授课之后，就迅速让学员走出户外，强调学员对户外建模活动的切身体验，对MCM任务和游踪的设计，对MCM－App和网站的实际操作和任务和游踪的教学实验；倡导“做中学”，让学员在“教师/学生”的身份之间来回转换。这有助于学员熟悉相关的技术操作，深化对户外建模活动的认识，领会MCM任务的设计原则和相关教学方法。

2. 培训议程多样，促进组内交流与协作

MoMaTrE培训项目设置了专家讲座，参观博物馆、学校，不同形式的游踪体验，任务设计，任务反馈，教学试验，任务修订等多样化的活动形式，给学员带来了丰富的培训体验和任务设计灵感，这有助于提高学员的兴趣和参与度。①陆彩霞, 姜媛, 方平, 等. 典型教师工作坊研修活动的特色分析与未来研究展望−−基于北京市典型教师工作坊的实践研究[J]. 教育科学研究, 2019(02): 87–92.其中后五项都是学员以小组为单位协作完成的，这有助于他们集思广益，发现更多的问题，获取更多的信息，也得到更多的启示和问题解决的方法。②同本页①。值得一提的是，每组学员都有专家（包括学科专家、教育研究者、有MCM教学经验的一线教师和项目团队成员）入组支持，这有助于及时响应教师需求，切实提高培训实效。

3. 多轮“设计−反馈−修订”循环，促进学员对任务的反思

MoMaTrE培训的另一个特点是包含多重设计−反馈循环。在本研究第二部分介绍的培训案例中，学员共经历了四次关于MCM任务的反馈：组内反馈，小组互相反馈（体验另一小组的数学游踪并给予反馈），专家反馈，以及最重要的教学实验反馈。反馈的形式和主体都呈现出多元化的特点。反馈的内容涉及任务难度的合理性，任务是否遵循在场性、清晰性，任务提示的渐进性等方面。每次反馈后，组内成员都会对本小组的任务和游踪进行修订。这有助于教师从多个角度对任务进行反思，进而不断改进任务质量、发展任务设计能力。

四、结语

（一）德国MCM项目的先进经验

德国MCM项目提出了信息技术与真实情景中的数学建模教学整合的新模式：教师在门户网站中创建MCM任务并投放到MCM－App上，通过MCM－App中的导航、分级提示和答案验证功能，支持学生在户外真实情景中的自主建模活动，培养其提炼现实模型和数学化的建模子能力，教师也减轻了自身在户外引领和实地教学干预中的工作量。项目同时以通用型任务“授之以渔”，注重任务的开放性、在场性和任务提示的启发性、渐进性，为教师任务设计提供高质量的参考；在网站中引入“公开”“复制”“粘贴”等功能，搭建资源交流共建平台；在教师培训中设置教师/学生双重视角和多重设计循环，推动教师多方位的实践、交流与反思。这些经验可以为我国数学建模或其他内容教学的创新改革提供许多借鉴。由于我国中学生数学建模的薄弱环节也常常在于提炼现实模型和数学化，十分适合引进MCM项目。目前MCM的门户网站和App都已推出了中文版，我国教师可以直接在网站中创建MCM任务和游踪，开展类似的户外教学。

（二）德国MCM项目的不足之处

MCM项目也存在一些不足。如通用型任务的主题分布不均，大多是几何类任务。通用型任务的数学活动性不强，以公式的直接应用、代入测量数据为主，如果教师在实际教学中重复设计此类任务，很容易让学生感到枯燥。再比如教师培训过分强调教师的主体地位，入组的学科专家通常只是回答教师提出的问题或是回应其观点，很少主动干预，使得教师在设计MCM任务和参与教学实验时容易出现随意性和盲目性。这些都是我国在引进MCM项目或推广类似教育创新项目时需要注意的问题。另外，MCM教学活动难以推动学生对模型的反思，因而也就难以促进学生建模能力水平全方位的提升。对此，教师可以将课堂教学和户外活动相结合，弥补学生对模型反思的不足。比如关于上文中的花盆问题，教师可以在回到课堂之后向学生展示三种不同的建模方案，让大家比较不同方案在该问题情景中的优势、缺陷，分析圆柱和圆台之间的关联。

（三）展望

在未来，MCM项目团队将考虑扩大移动设备的优势，比如在MCM－App的提示系统中引入增强现实（Augmented Reality，简称AR）等适用于移动设备的技术。图10展示了普通AR技术和一个MCM任务结合的应用场景，屏幕上同时给出任务内容，现实对象和虚拟的AR对象。在该影像的提示下，学生很容易就能想到任务中的底座可以近似为一个正方体与长方体，进而完成相关的建模求解；学生还可以对该AR对象进行分离、旋转等操作。①CAHYONO A N, SUKESTIYARNO Y L, ASIKIN M, et al. Learning mathematical modelling with augmented reality mobile m ath trails program: How can it work?[J]. Journal on Mathematics Education, 2020, 11(2): 181–192.

图10 普通AR技术的与MCM任务结合

图11 展示了GeoGebra 3D Calculator中的AR技术和MCM任务结合的场景，学生在这里可以直接构造虚拟的AR对象，完成建模。①LAVICZA Z, HAAS B, KREIS Y. Discovering Everyday Mathematical Situations Outside the Classroom with MathCityMap and GeoGebra 3D[C]//LUDWIG M, JABLONSKI S, CALDEIRA A, et al. Research on Outdoor STEM Education in the digiTal Age: Proceedings of the ROSETA Online Conference. Münster: WTM, 2020: 111–118.但截至目前，这些AR技术都没能与MCM－App原有的功能完全整合起来，学生在新型的MCM－App中看到AR交互界面的同时，常常无法输入答案并对其进行验证。这也是项目团队在未来研发中需要解决的问题。我国在开展数学建模创新教育时，也可以考虑适当引入AR技术，为学生的数学建模过程提供更有效的支持。

图11 GeoGebra 3D Calculator AR技术与MCM任务结合的场景