重型车辆多挡并联混合动力系统的联合优化控制策略

王玮琪， 王伟达，2， 孙晓霞， 张渊博， 刘城， 项昌乐，2

(1.北京理工大学 机械与车辆学院， 北京 100081； 2.北京理工大学 重庆创新中心， 重庆 401122；3.中国北方车辆研究所， 北京 100072)

0 引言

重型车辆的机动性和动力性一直是人们关注的重点。随着重型车辆后勤补给困难程度的日益增加，重型车辆电传动技术得到了快速发展，采用混合动力系统的重型车辆即在此背景下发展而来。它可实现电传动或机械传动，充分发挥发动机或者动力电池组等动力源的优点，实现低油耗、低排放等目标，具有良好的应用和发展前景。根据动力系统的不同布置形式，混合动力车辆可分为串联式混合动力车辆、并联式混合动力车辆以及混联式混合动力车辆。并联式混合动力是常见的混合动力形式，尤其是发动机和电机在变速箱内进行动力耦合的多挡并联系统，由于发动机和电机传递通道上具有不同的挡位，其动力耦合比例和功率匹配具有更大的灵活性，具有优异的混合驱动性能。

基于规则的能量管理策略，以及基于优化的能量管理策略，是目前国内外使用较为广泛的能量管理策略[1]。基于规则的方法较简单，容易被实现，因此在实际的控制中得到了广泛应用。基于优化的能量管理策略包括瞬时优化型和全局优化型。瞬时优化控制策略主要包括等效最小燃油消耗策略、鲁棒控制方法、解耦控制等，计算量较低是它的优点，多应用于混合动力车辆的实时控制。全局优化策略虽然有着较为优秀的优化效果，但却因为需要提前了解工况信息以及计算量太大等缺点，很难应用于车辆的实时控制中[2]。

自动变速器(AMT)最核心的部分即是换挡规律，其主要内容为各挡位换挡时机随控制参数的变化规律[3]。换挡规律对混合动力车辆的经济性和动力性等非常重要，可以根据计算原理把换挡规律分为智能换挡规律与传统换挡规律[4]。混合动力车辆换挡规律与其工作模式息息相关，文献[5]研究结果显示，混合动力车辆在不同的工作模式下，换挡规律存在一定的差异。

混合动力车辆的动力源之间存在相互协同关系，如果换挡规律的性能指标制定方法不同，则即便是相同的动力传递系统，各个部件也会发挥完全不同的潜能，产生不同的效果，不论对于车辆的舒适性、经济性还是动力性，都会产生较大的影响。目前，在能量管理方面的策略主要通过优化发动机和电机的工作点位置，使它们尽可能多地工作在高效区间，通过这种方法来提高整车经济性。但是目前仍存在两方面问题：一是没有考虑电机的工作效率，二是难以适应车辆实际运行过程中出现的动态变化[6]。

本文针对某构型多挡并联混合动力系统，在分析构型特点基础上，综合考虑发动机和电机的工作效率，分别建立不同工作模式的综合效率和换挡成本函数模型。以系统综合效率和换挡成本最优设计联合优化控制策略，用自适应模拟退火(SA)算法进行求解。对于变速器工作挡位以及转矩分配实时在线进行优化，以使整车的综合效率得到加强。建立基于MATLAB/Simulink软件和AVL Cruise软件的联合仿真模型，提升仿真精度，对提出的联合优化控制策略进行了仿真测试与验证。

1 多挡并联混合动力方案

如图1所示，重型车辆多挡并联混合动力系统主要由电动机、离合器、AMT、主减速器、发动机以及动力电池组等组成。

图1 多挡并联插电式混合动力系统结构图Fig.1 Structure diagram of multi-gear PHEV

重型车辆的工作模式如表1所示，主要分为纯电动模式、混合动力模式、行车充电模式、反馈制动模式[7]。当电池的荷电状态(SOC)低时，行车充电的模式是更为适合的，本文的行车充电模式中包括了发动机单独驱动。混合动力车辆行驶过程中，电机是否参与以及参与程度大小，在很大程度上决定了混合动力车辆的经济性。

表1 车辆工作模式Tab.1 Working modes of PHEV

多挡并联的混合动力系统有两路独立的动力传递路径，因此在换挡时可以交替提升或降低机械路或电动路的挡位，从而保证了动力输出不间断，避免了换挡时的动力中断且换挡响应时间更短[8]；机械和电力功率互相影响，但又有分别地传递通道及挡位，为不同挡位组合下的转矩分配增加了难度。

2 基于系统综合效率的联合优化策略

2.1 系统综合效率定义

重型车辆尤其是特种车辆混合动力系统由于大功率和高机动性要求，不宜采用汽车常用的燃油消耗最小为基本优化目标的能量优化方法，在保证动力性要求前提下优化混合动力系统的效率和燃油消耗率，更符合特种重型车辆的能量管理要求。多挡并联混合动力系统涉及发动机、电机、变速机构等多个功率传递部件，动力源与挡位组合复杂多样，难以简单描述传动效率。本文从分析不同模式的并联混合动力系统构型与功率流传递路径出发，提出系统综合效率[9]的计算方法。已知系统输出功率与系统输入功率的比值通常被定义为混合动力系统的综合效率。由于车辆功率的流动方向会随着车辆运行模式的改变而发生变化，带来的影响就是之前计算方法出现误差，因此车辆在不同模式下的计算方式需要进行更改。

限于篇幅，下面以混合驱动模式为例给出综合效率的计算公式。混合驱动模式功率流通道如图2所示。图2中：ηb为电池充放电效率；Pm为电机功率(kW)，ηmm为电机的电动效率，Pm、ηmm由电动机工作点计算或查表得到；Pe为发动机功率(kW)；ηt为传动系统的效率；ηe为发动机效率，

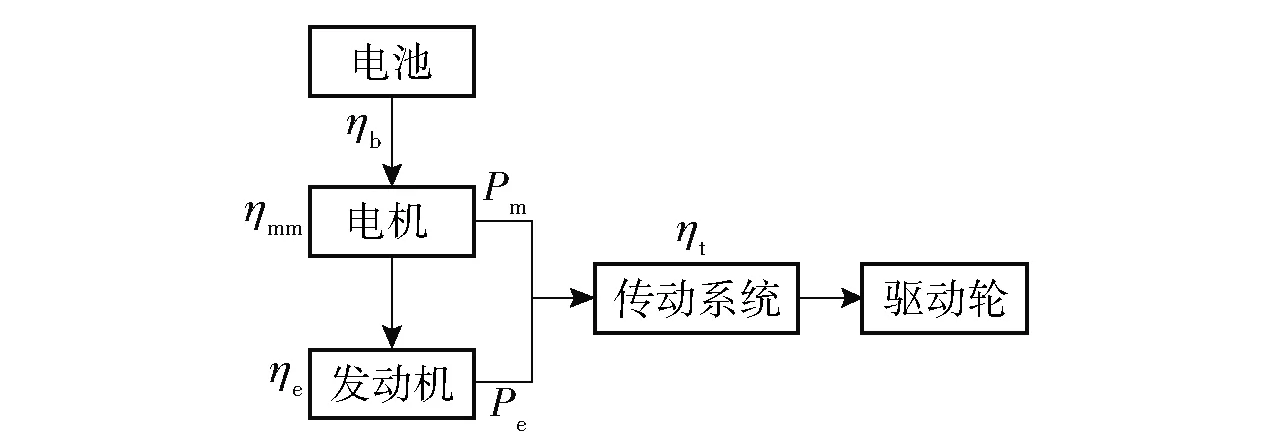
图2 混合驱动模式功率流示意图Fig.2 Power flow of hybrid drive mode

(1)

ge和hf分别为发动机燃油消耗率和燃油热值。

混合动力模式的综合效率ηh[10]可表示为(2)式形式：

(2)

(3)

(4)

式中：Te为发动机转矩(N·m)；ne为发动机转速(r/min)；Tm为电机转矩(N·m)；nm为电机转速(r/min)。

纯电动模式的综合效率ηev可表示为(5)式形式：

(5)

行车充电模式的综合效率ηc可表示为(6)式形式：

(6)

式中：ηmc为电机充电效率。

2.2 基于综合效率最优的联合优化控制策略

基于系统综合效率最优的联合优化控制策略，为了保证车辆的运行效率可以每时每刻达到最高，首先需要将车辆的工作模式通过车速、油门开度、电池SOC等参数确定。随后根据该模式计算发动机需求转矩、电机需求转矩、AMT目标挡位等瞬时最优控制量[11]。基于系统综合效率最优的联合优化控制策略如图3所示。

图3中，nm,max为电机最大转速，Tm,max为电机在电动机模式下最大转矩，gear为变速器挡位，gearmax为变速器最高挡位，gearmin为变速器最低挡位，costη为重型混合动力车辆的综合效率成本，costgear为重型混合动力车辆的换挡成本，J为每个控制周期的成本函数，ω为出现频繁换挡时的惩罚系数，ne,max为发动机最高转速，ne,min为发动机最低转速，Te,max为发动机最大转矩，Te,min为发动机最小转矩，Tg,max为电机在发电机模式下的最大转矩。

2.2.1 成本函数构造

从重型混合动力车辆的实际需求出发，选取系统综合效率和换挡成本构造瞬时成本函数[12]。从理论上，达到上述两个目标是矛盾的。因为提升系统的综合效率需要挡位与速度时刻匹配，但是换挡操作过于频繁会导致系统不稳定，所以需要综合考虑这对矛盾因素。成本函数可表示为

J=costη+ω·costgear.

(7)

当ω数值较小时，系统对于换挡呈现鼓励态度；其数值增大到一定程度时，换挡代价随之增加，会抑制换挡。

不同工作模式下重型混合动力车辆的综合效率成本，可以通过定义的计算方法计算如下：

(8)

式中：costη取为负值，其值越大表示成本越小；Pb为电池的充放电功率，Pb大于0 kW时放电，Pb小于0 kW时充电，其计算公式如下：

(9)

本文提出的联合优化控制策略为了追求系统综合效率最大化，通过计算来得出最佳转矩分配比例以及挡位，因此稳态的换挡规律曲线是没有参考价值的。将瞬时寻优过程中的目标挡位和AMT当前挡位差值的平方costgear设为成本函数的一部分，可以有效避免出现频繁换挡的情况，costgear可以表示为(10)式形式：

costgear=[gear(k+1)-gear(k)]2，

(10)

式中：gear(k+1)表示当前控制周期的目标挡位；gear(k)表示AMT当前挡位，即为由上一个控制周期计算得出的最优挡位[13]。联合优化策略通过使得每个控制周期成本函数J最小来计算得到优化控制解，见(11)式：

uopt=arg minJ，

(11)

式中：uopt为计算得出的最优控制量。

2.2.2 可行域分析

混合动力车辆的联合优化控制策略在求解优化解的过程中，需要保证发动机和电机的转速均在许用区间内。发动机和电机转矩等控制量均不能超过当前转速下的最大值。同时，发动机和电机在不同模式下的工作状态不完全相同，优化过程中的可行域也有一定差别。

2.2.2.1 纯电动模式

车辆处于纯电动模式时，驱动转矩不由发动机提供，全部由电机提供，因此优化过程中的搜索问题为一维。由于发动机、电动机为并联构型，转速与地面不解耦，应满足等式约束为

(12)

(13)

式中：v为汽车车速；ig,em为电动路挡位传动比；i0为主减速器速比；r为汽车车轮半径。

2.2.2.2 混合驱动模式

当车辆处于混合驱动模式时，驱动转矩既由发动机提供，也由电动机提供，当变速器的挡位出现改变时，电动机和发动机的转矩组合方式会出现多种形式[14]。优化过程中，发动机和电动机都需要考虑在内，因此搜索问题为二维，转速应满足的等式约束为

(14)

(15)

(16)

式中：ig,ce为机械路挡位传动比。

2.2.2.3 行车充电模式

当车辆处于行车充电模式时，驱动转矩由发动机提供，发动机转矩大于0 N·m，而电机转矩处于小于或等于0 N·m的状态，转速应满足等式约束为

(17)

(18)

为了加快寻优速度，可以通过缩小优化范围等方法实现。同时也为了保证不出现跳挡情况及变速器顺序升降挡，可以把当前挡位和相邻变速器挡位设置为优化区间，从而可以通过利用上一步结果来得到最优结果[15]。下一时刻的挡位可由(19)式表示：

gear(k+1)=gear(k)+shift(k),gearmin≤
gear(k+1)≤gearmax，

(19)

式中：shift(k)为当前控制周期的换挡指令，

(20)

2.2.3 求解过程

步骤1通过当下时刻的油门开度信息和车辆的行驶速度来计算整车需求转矩Tr.

步骤2根据当前电池SOC状态与需求转矩Tr，并且通过工作模式切换原则，确定接下来车辆运行的目标工作模式，此时许用挡位范围可以通过AMT当前挡位和工作模式确定。

步骤3循环AMT挡位，根据当前车辆行驶速度来计算发动机和电机的转速ne、nm.假如计算得出的发动机和电机的转速超出了二者的可行域，则当前的工作点为不可行工作点，舍去此时电机和发动机的转速点。

步骤4将发动机峰值外特性曲线与步骤3中求得的可行发动机转速点相结合，得出的数值即为发动机转矩范围，离散此转矩。

步骤5循环发动机转矩，主要根据目前需要的转矩Tr以及当前变速器的挡位，计算目前所需电机转矩，如超过可行域范围，则将其作为不可行的工作点，舍去。

步骤6选取一组可行工作点(Te，ne)、(Tm，nm)，计算出每一个工作模式下的效率成本，并把换挡成本计算出来，根据定义计算成本函数J.

步骤7重复步骤6，直至得到使成本函数J最小的一组电机和发动机工作点(Te,opt，ne,opt)、(Tm,opt，nm,opt)，此为最优工作点，所对应的挡位即为最佳目标挡位。

2.3 求解算法

SA算法是由Metronpolis等提出的全局优化算法，其通常被应用在求解最小能量函数问题，可以找到能量函数的最小最优解[16]。随后的自适应模拟退火(ASA)算法由Wu等[17]提出并进行改进，有效降低算法的敏感性，这样做的好处是相对于SA算法，可以获得更好的计算效率和求解能力。任何系统和目标函数都可以通过ASA算法进行计算和处理。鉴于ASA算法的突出优点，本文采用ASA算法对联合优化控制策略进行优化。

3 仿真结果及验证

基于MATLAB/Simulink和AVL Cruise软件搭建的联合仿真平台，以新欧洲驾驶周期(NEDC)为例对提出的联合优化控制策略进行仿真验证。

电平衡油耗指标是主要对比指标，其主要内容是将电量保持阶段的门限值定为电池初始SOC，并保持SOC变化范围控制在3%以内计算得到能耗值。这样对于插电式混合动力车辆的节油效果有更好的反映。仿真结果如图4所示。为进行对比分析，基于规则策略和经济性换挡规律的仿真结果如图5所示。

比较图4和图5的结果可以看出：在联合优化策略控制下，混合动力车辆可以很好地跟随NEDC工况，并且发动机的转速保持在1 800～3 000 r/min的高效区域，电量保持阶段的SOC可以保持平衡且在最终时刻的偏差量被控制在3%以内，且相比一般经济性换挡规律明显减少了换挡次数。

图4 联合优化控制策略仿真结果Fig.4 Simulated results of joint optimal control strategy

图5 规则控制策略主要仿真结果Fig.5 Main simulated results of rule control strategy

发动机的工作点位密集分布在发动机燃油消耗率最低的几个区域，而不再是分布于最佳燃油经济性曲线附近。与此同时，为了提高电机的工作效率，联合优化控制策略提升了电动机的工作转速，使电动机的工作效率得到了提升，工作点趋向于高效区。

表2所示为不同控制策略下所产生的电平衡油耗。由表2可见，联合优化控制策略控制下的混合动力车辆与使用经济性换挡规律规则的车辆相比可以减少4.84%的油耗、与使用初始单参数换挡规律相比可以减少14.74%的油耗。

表2 电平衡油耗对比Tab.2 Comparison of fuel consumptions of electric balance

4 结论

本文计算了不同模式下车辆的综合效率，系统地描述了多种模式多种挡位组合下的系统功率损失，建立了机电功率分配联合优化模型。引入成本函数，综合考虑换挡次数与系统稳定这对矛盾因素，从而对功率分配与挡位进行联合优化。最后，通过ASA算法对该策略求优化解。仿真结果表明：联合优化控制策略控制下的混合动力车辆与使用经济性换挡规律规则的车辆相比可减少4.84%的油耗、与使用初始单参数换挡规律相比可减少14.74%的油耗，有效提高了重型多挡并联混合动力车辆的经济性。