双侧电机耦合驱动履带车辆斜坡转向控制策略

曾根， 王伟达， 盖江涛， 马长军， 李训明， 李欢欢

(1.北京理工大学 机械与车辆学院， 北京 100081； 2.中国北方车辆研究所， 北京 100072)

0 引言

转向是一种履带车辆典型的行驶工况，而斜坡转向由于受到重力沿斜坡分力的影响，其动力学特性与平面转向相差很大，现有的履带车辆转向理论[1-5]主要针对平地转向进行运动学和动力学分析，缺少斜坡转向方面的理论研究，驾驶难度较大，车辆的平稳以及可控性较差。与液力机械综合传动的履带车辆相比，采用电驱动可以实现无级变速，效率高，易于布置，适合采用现代控制技术[6]。对电驱动车辆而言，斜坡转向可以通过控制策略克服两侧不同的转向阻力，实现较精确的转向控制。

针对不同的电机控制指令，转向控制策略可以分为控制电机转速和控制电机转矩两种[7-9]。采用转速控制策略时，驾驶员操纵信号解析为目标转速，电机利用PID控制转速环，由于转速指令与目标驱动转矩之间是非线性关系，加上车辆自身惯量影响，利用PID精确解算转矩有一定的难度，实际斜坡转向过程不一定稳定[10-13]。采用转矩控制策略时，驾驶员操纵信号直接解析为目标转矩，电机控制较为简单，但是在负载转矩实时变化时，必然导致操控性及转向稳定性较差。

本文针对双侧电机耦合驱动履带车辆在斜坡转向控制过程中的动力学相关特性进行分析，实时确定两侧履带牵引力的大小和变化，通过运动状态多变量预测控制，解决双侧电机耦合、地面负载、坡度等相互耦合问题，以实现履带车辆在任意坡度角、任意速度下的平稳转向控制。

1 电传动履带车辆斜坡转向过程描述

1.1 双侧电机耦合驱动履带车辆转向原理

双侧电机耦合驱动是机电复合传动的一种形式，传动综合控制器根据驾驶员的操作指令，依据控制策略计算出两侧电机的控制指令，通过总线下发给响应的电机控制器。双侧电机耦合驱动系统由左右两侧驱动电机、耦合机构功率组成[14]，如图1所示。图1中：kl、kr、ko分别为左右两侧普通减速排以及中间双星复合排的特征参数，其中，kl=kr=k，ko=1，k为减速行星排参数；kb为变速行星排参数；ic为侧传动比。

图1 双侧电机耦合驱动结构简图Fig.1 Structural diagram of dual motor coupling drive transmission

由图1可见：电机从直流母线上获取直流电，经过直流/交流(DC/AC)驱动电机转动；左右电机经过变速机构后传到耦合机构，直驶时耦合机构整体回转，转向工况时利用耦合机构进行差速差矩，完成相应的转向过程，耦合机构将双侧电机的变速和转向功能有机结合在一起。设nml、nmr分别为左右侧电机的转速，Tml、Tmr分别为左右电机的转矩，nol、nor分别为左右主动轮的转速，Tol、Tor分别为左右主动轮的转矩[15]，变速排为两挡，传动比分别为ib1、ib2，写成集合形式为ib={ib1,ib2}.

对电传动装置进行转向运动学分析，得到输入输出转速关系[15]如下：

(1)

(2)

履带车辆的相对转向半径ρ以及车速v分别为

(3)

式中：rz为主动轮半径。

1.2 履带斜坡转向模型

转向工况下的运动为复合运动，车辆一方面绕转向中心转动，另一方面绕低速侧履带接地中心转动，综合考虑车辆转向中心偏移、履带滑转滑移等因素，建立斜坡转向模型。首先对斜坡转向过程进行分析，斜坡角度为α，车辆斜坡上的方位角为β，建立图2所示参考坐标系。图2中：Oxyz为固定于地面的空间直角坐标系；Oixiyizi为内侧履带接地中心坐标系，Oi为内侧履带接地中心；O′x′y′z′为固定在车辆上随动空间直角坐标系，O′为履带车辆几何接地中心；Ooxoyozo为外侧履带接地中心坐标系，Oo为外侧履带接地中心；Mr为两侧履带所受到的转向阻力矩的合力矩；ax为车辆转向中心在x轴方向的偏移量；ay为车辆转向中心在y轴方向的偏移量；No为履带外侧的接地压力；Ni为履带内侧的接地压力；G为履带车辆重力；O″为履带车辆在斜坡上的瞬时转向中心。

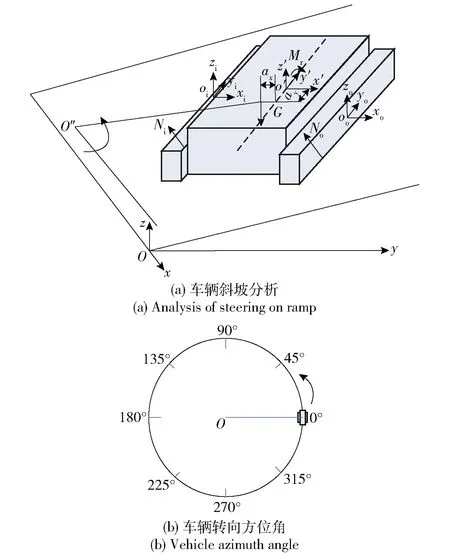
图2 车辆斜坡转向过程Fig.2 Process of steering on ramp and azimuth angle

下面以履带车辆方位角在0°～90°的情况为例进行分析。同时，取转向工况内侧为低速侧，外侧为高速侧，做出如下假设：

1) 车辆转向过程中转向半径R固定；

2) 斜坡为平面；

3) 履带所受地面的力垂直地面反向呈线性分布，且横向阻力与单位履带上的载荷呈线性关系；

4) 不考虑车辆纵向俯仰和横摆，车辆绕垂直地面的轴转动；

5) 假设履带无拉伸，形状不变。

根据履带接地的压力分布，可以得到两侧履带的接地压力，如图3所示。图3中：Fx为车辆所受横向合外力，它与离心力的横向分量Fx′相等；Fy为车辆所受纵向合外力，它与离心力的纵向分量Fy′相等；外侧履带接地端前后两端所受单位长度法向负荷分别为qoh、qoq.图4所示为履带所受平行于路面的横向力分布情况，其中L为履带接地长，B为履带中心距，Fi、Fo分别为履带内外两侧的驱动力，FRi、FRo分别为履带两侧所受的行驶阻力；qiay、qoay分别为履带横向力梯形的中间值，qih、qiq分别为内侧履带接地端前后两端所受单位长度法向负荷。

图3 斜坡履带接地压力分布Fig.3 Distribution of ground pressure on ramp

履带纵向行驶阻力与接地压力呈正比，由此可以得到两侧行驶时的滚动阻力[2]为

(4)

式中：hg为履带车辆中心高度；f为阻力系数。

转向阻力矩Mμ等于图4横向阻力梯形图中梯形面积对履带中心点取矩[16]，具体计算公式如下：

(5)

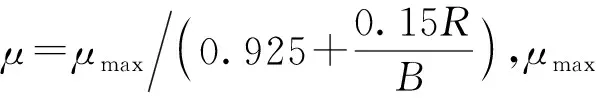
(6)

根据上述受力分析，建立车辆斜坡转向动力学模型如下：

(7)

式中：I为履带车辆绕转向中心的转动惯量；ω为履带车辆转向角速度。

驱动力与驱动扭矩之间的关系如(8)式所示：

(8)

式中：Ti、To分别为内外两侧主动轮扭矩。

2 基于模型预测斜坡转向控制策略

对于传统的履带车辆，在斜坡转向过程中对驱动力的控制和行驶方向修正只能依靠驾驶员的经验和感觉[17]。本文研究的双侧电机耦合驱动履带车辆斜坡转向控制策略，要求在转向过程中，根据驾驶员加速踏板、方向盘转角确定履带车辆的期望车速以及转向角速度，使得车辆所处不同坡度、不同方位角下，实时修正调节电机的输出转矩，完成斜坡转向驾驶意图。

建立图5所示斜坡转向状态多变量预测控制系统。图5中，v*、ω*为按驾驶员意图给定的需求速度以及转向角速度，vr、ωr分别为系统实际输出值，Fml、Fmr分别为电机驱动力解算模块得出的初始电机驱动力，F1、F2分别为预测模型输出的左右侧电机补偿驱动力，Fl、Fr分别为左右侧电机实际输出驱动力，nrl、nrr分别为左右侧电机实际转速。

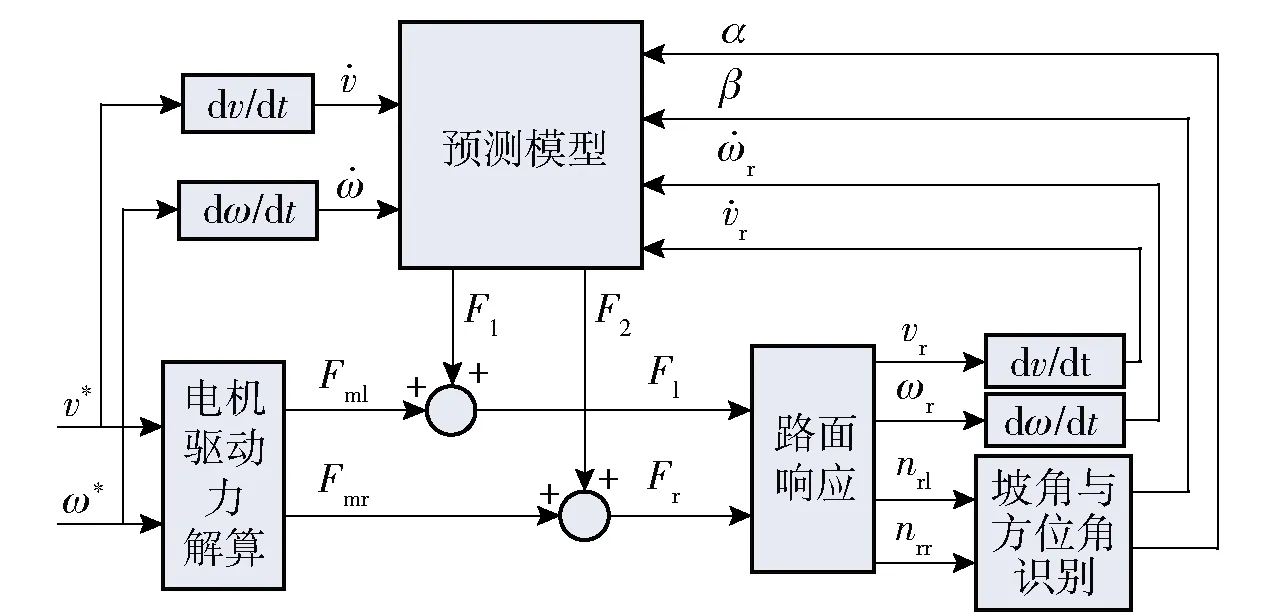
图5 斜坡转向控制策略Fig.5 Steering on ramp control strategy

斜坡转向控制策略的预测模型是以两侧履带的目标加速度以及目标角加速度作为输入，预测车辆斜坡转向两侧履带实际所需的驱动力，预测模型为

(9)

式中：m为履带车辆质量；Iri、Iro分别为车辆内外两侧主动轮的转动惯量。

由图5可见：电机解算模块通过输入目标转速与转向半径进行电机转矩的初步计算，通过主动轮实际输出的转速得到当前的车速vr与转向角速度ωr，结合控制输出的驱动力Fl与Fr；利用(7)式获得当前的Mμ与FRo，通过(4)式进行坡度角α与方位角β的识别；最后通过对期望的车速v*与角速度ω*求积分，通过多状态变量进行预测控制输出，对电机驱动力解算模块进行调整，使履带车辆完成期望的车速与转向半径，从而实现坡道上不同方位角的转向控制。

3 斜坡转向控制策略仿真分析

应用MATLAB/Simulink软件对履带车辆斜坡转向动力学以及转向控制策略进行建模，履带车辆参数按照实际试验的车辆参数，该车主要参数如下：车体质量m=23 000 kg；履带中心距B=2.75 m，履带接地长L=4.4 m；质心位置距地高hg=1.2 m；安装金属履带，地面参数f=0.04，μmax=0.68.车辆沿一定的车速及转向半径旋转一周，规定转向过程中逆时针转向为正，半实物仿真系统如图6所示。

图6 半实物仿真系统Fig.6 Hardware-in-the-loop simulation system

仿真结果通过图7、图8给出。图7所示为转向半径20 m下不同坡度内外两侧履带所需的牵引力随车辆方位角变化的曲线。从图7中可以看出：外侧履带在0°～50°和250°～360°范围内，牵引力随坡道角度增加而增大；在60°～220°范围内，外侧履带由牵引变为制动状态，且随着坡度增加所需制动力也随之增加；在100°～150°范围内，外侧转矩发生变化，主要是因为阻力矩随着转向减小而减小；内侧履带在45°～270°之间为牵引状态，且所需牵引力随着坡度增加而增加。分析整个转向过程可以看出，斜坡转向控制策略根据相应坡度控制电机转矩，使车辆保持稳定的斜坡转向过程。

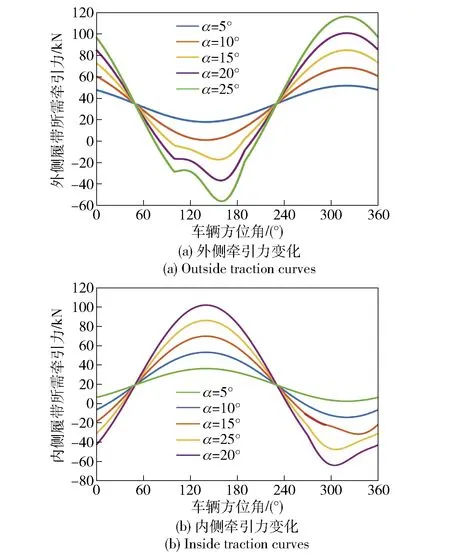
图7 相同转向半径、不同坡度下牵引力变化曲线(R=20 m)Fig.7 Inside and outside traction forces at different ramps and same steering radius(R=20 m)

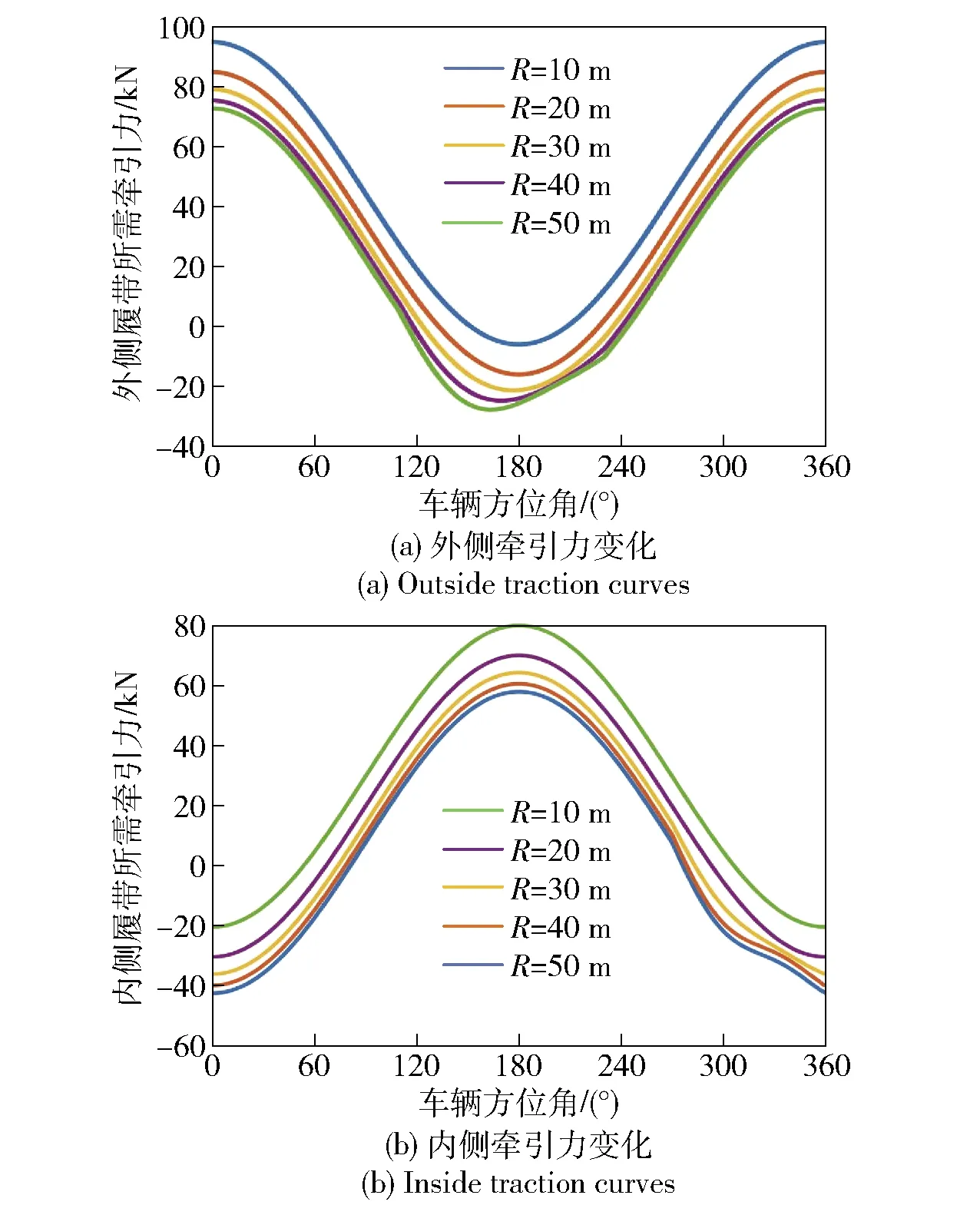
图8 相同坡度、不同转向半径下牵引力变化曲线(α=15°)Fig.8 Inside and outside traction forces at different steering radii and same ramp(α=15°)

图8所示为坡度角15°下以不同的转向半径转向时内外两侧履带所需牵引力随车辆方位角变化的曲线。从图8中可以看出：内外两侧履带的牵引力随着转向半径的变化几乎呈比例变化，但是在下坡过程中，由于重力分力的影响，内外两侧履带的牵引力发生微小变化；随着转向半径的增大，转向阻力矩减小，内外两侧所需的相应制动力、牵引力均减小。分析整个转向过程可以看出，斜坡转向控制策略根据相应坡度控制电机转矩，使车辆保持稳定的斜坡转向过程。

4 控制策略实车验证

本文试验场地为坚硬的水泥地面，履带车辆的转向半径以及车速通过主动轮转速计算得到，主动轮转速采用电机转速通过双侧电机耦合驱动传动比关系计算得到，电机转速通过电机控制器采集电机的角位置信号获得。主动轮转矩也是采用电机转矩通过双电机耦合驱动传动比关系计算得到，电机转矩通过电机控制器采集电机三相电流通过相应算法得到。

受场地限制，无法模拟斜坡0°～360°的转向全过程，为了能够验证斜坡转向控制策略，如图2方位角图所示，取0°～90°爬坡转向以及180°～270°下坡转向两个工况进行试验。

上坡试验结果如图9所示。由于上坡阻力较大，车辆行驶缓慢，驾驶员驾驶车辆，使履带车辆处于较平稳的爬坡转向过程，在v取值为5.5～6.2 km/h，ρ取值为2.5～3.0情况下，内侧电机转速趋于0 r/min，外侧达到1 300 r/min左右，将实际车速与转向半径作为斜坡转向模型的输入(见图9(c)与图9(d))，可以看出模型计算的电机转速与转速具有较高的精度，故基于斜坡转向模型提出的模型预测控制策略，车辆能够稳定转向，操控性良好。

图9 上坡过程试验结果Fig.9 Results of upgrades on ramp

下坡试验结果如图10所示。由于下坡过程，车辆受自身重力，车速会加快，驾驶员驾驶车辆，使履带车辆尽量平稳行驶。从图10中可以看出：车速在不断增大，相对转向半径基本稳定在3～4范围内，左右侧电机转速不断增大，但是速度差保持一定。实际车速与相对转向半径作为斜坡转向模型的输入，如图10(c)与图10(d)所示，从中可见：本文所提模型计算的电机转速与转速具有较高的精度；基于本文模型预测控制策略，车辆能够稳定转向，操控性良好。

图10 下坡过程试验结果Fig.10 Results of downgrades on ramp

5 结论

本文针对双侧电机耦合驱动履带车辆，进行了运动学与动力学分析，建立了履带斜坡转向动力学模型，同时提出了基于模型预测的斜坡转向控制策略，给出了预测计算方法，通过MATLAB/Simulink软件进行了仿真与试车验证。研究结果表明，该履带车辆斜坡转向模型具有较高的可信性，基于模型预测的斜坡转向控制策略能够按照驾驶员意图，在不同斜坡坡度与车辆运行不同的方位角下，使履带车辆稳定地进行斜坡转向。