基于改进MPC 的UPS 系统三相逆变器控制策略研究

徐秀英

(鄂尔多斯职业学院自动化与信息工程系，内蒙古 鄂尔多斯 017010)

三相逆变器的控制是电力电子技术中最重要和最经典的主题之一，并且在过去的几十年中已经进行了广泛的研究[1－2]。在需要高质量电压的应用中，带有输出LC 滤波器的逆变器的控制尤为重要，例如分布式发电和不间断电源(Uninterruptible Power Supply，UPS)。特别是对于UPS 系统，希望在任何负载(通常是非线性负载)下都能达到良好的输出电压波形[3]。因此，高性能UPS 的主要要求是在各种负载下UPS 逆变器输出电压中的总谐波失真(Total Harmonic Distortion，THD)低以及动态响应速度快，包含输出LC 滤波器可以使逆变器提供高质量的正弦电压，对输出电压的高要求使控制器设计和参数调整更加困难[4－5]。

国内外学者已经为转换器提出了几种控制方案，包括非线性方法[6](如磁滞控制)、线性方法[7](如使用脉宽调制的比例积分控制器)、无差拍控制[8]、双环PI 控制[9]、闭环控制[10]以及基于最少拍和重复控制[11]。在大多数控制方案中，输出电压和电流中的一种用于考虑外部和内部控制回路的级联控制，使用线性或非线性控制器和一个调制器来生成逆变器开关的驱动信号。

预测控制由于其快速的动态响应而在功率转换器中具有大量的实际应用。它可以应用于各种系统，可以轻松地包含约束和非线性，可以考虑多变量情况，并且易于实现最终的控制器设计[12－13]。预测控制需要大量的计算，然而当今可用的快速微处理器使实施预测控制成为可能。研究人员以预测控制的名义提出了几种控制算法。这些控制方案的一种众所周知的类型是模型预测控制(Model Predictive Control，MPC)。对于功率转换器和驱动器的控制，MPC 是一种非常高效和易于实施的选择[14－17]。MPC 在预设的时间区域内使用系统模型来预测变量的行为，并且使用成本函数作为选择最佳未来行动的准则。为了简化MPC 的实现，可以将转换器建模为具有有限数量开关状态的系统，并且仅考虑一个时间步长即可实现系统优化。这种独特的优化方式可以在线评估所有开关的不同状态，然后以成本函数最小化选择特定开关的状态。MPC 优化时也可以考虑使用不同的预测范围来改善系统的性能，但会增加系统的复杂性和计算成本[18－19]。

本文提出了具有两步预测步骤的带输出LC 滤波器的三相逆变器模型预测控制策略。控制器使用系统模型来预测每个采样间隔内每种可能的开关状态的输出电压行为。然后，将成本函数用作选择在输出电压期间选择开关状态的标准。不需要内部电流控制环路，也不需要调制器，栅极驱动信号直接由控制器产生。根据输出电压的THD 和达到稳态操作的时间来衡量优化效果。将结果与仅进行一步预测的同一系统进行了比较，并考虑了线性和非线性负载，以验证所提出的MPC 的可行性和良好的性能。

1 系统模型

本文考虑的三相逆变器拓扑如图1 所示。此处介绍了转换器和滤波器模型，并且假定负载未知。转换器的开关状态由门控信号Sa、Sb和Sc确定:

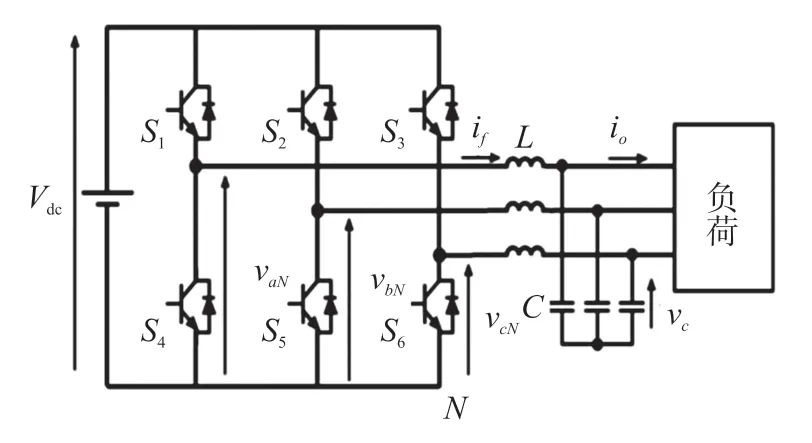
图1 带有输出LC 滤波器的三相逆变器

可用矢量形式表示为:

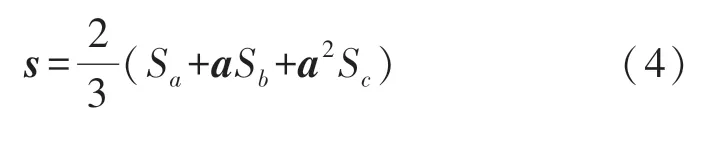
式中:a表示A 相的单位法向量。

本文假设开关器件都是理想的开关，因此不考虑开关和断开的过程。由逆变器产生的输出电压空间矢量定义为:

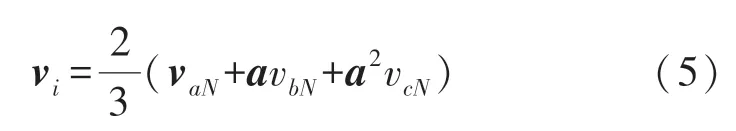
式中:vaN、vbN和vcN是逆变器的相电压，相对于直流母线N的负端。负载电压矢量vi可以使用开关状态矢量s和直流电压Vdc表示:

表1 表示考虑门控信号Sa、Sb和Sc的所有可能组合，使用式(6)获得八个开关状态，进而获得八个电压矢量。本文中变量Sa、Sb和Sc表示逆变器的a、b和c分支的开关状态。如图2 所示，由于v0＝v7，故仅产生七个不同的电压矢量。

表1 三相逆变器的开关状态和电压矢量

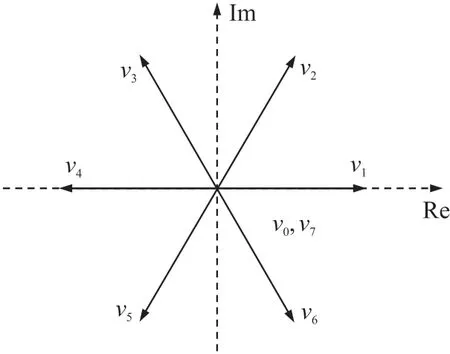
图2 逆变器电压矢量分布

在本文中，逆变器被建模为非线性离散系统，只有七个不同的电压矢量作为可能的输出。利用矢量表示法，滤波电流if、输出电压vc、输出电流io可以表示为空间向量，定义为:

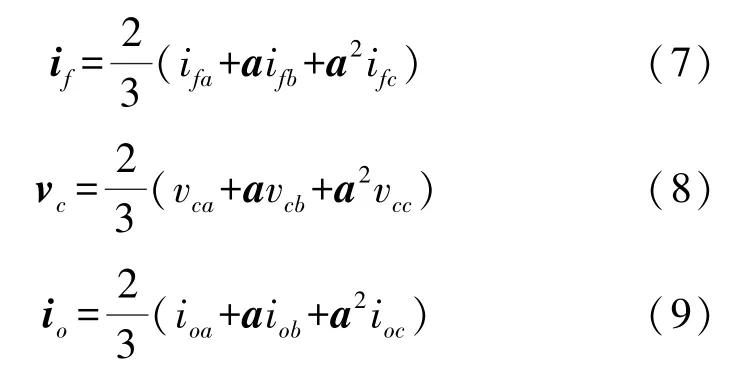
以矢量形式表示的滤波器电感方程为:

式中:L为滤波器电感。输出电压的动态特性可以用以下方式表示:

式中:C为滤波器电容。上述方程可以改写为状态空间系统，具体为:

由式(12)得到采样时间Ts的滤波器离散时间模型，表示为:

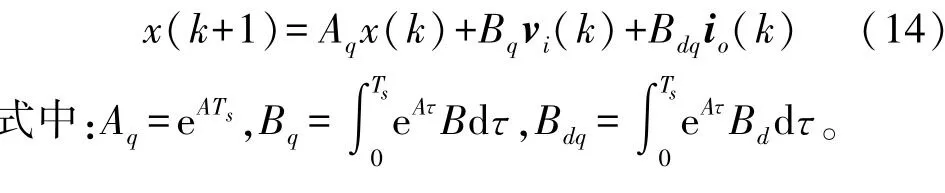
该模型用于计算给定输入电压矢量vi的输出电压vc的预测，并使用预测控制方案选择最佳电压矢量。为了使用式(14)预测输出电压vc，需要求输出电流。因此，可以使用从式(11)获得的以下方程式进行估算，具体为:

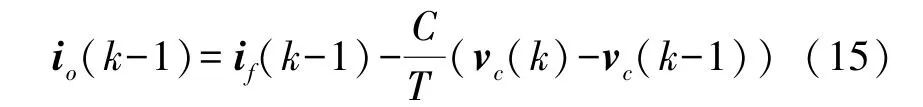
对于足够短的采样时间Ts，可以假设输出负载在一个采样时间内没有明显变化，并且在这种情况下io(k－1)＝io(k)。

2 模型预测控制

本节提出了使用具有不同预测范围的MPC 来控制功率变换器的方法。由于MPC 快速的动态响应，因此适合控制此类系统。MPC 可以应用于各种系统，可以轻松地包含系统约束和非线性，可以考虑多变量情况，并且易于实现最终的控制器。考虑了逆变器只能生成七个不同的输出电压矢量，利用此特点，可以设计在线解决MPC 优化问题。

考虑到一步预测步长N＝1，带有输出LC 滤波器的三相逆变器的MPC 的框图如图3 所示。在采样时间k处，MPC 的控制步骤如下所述:

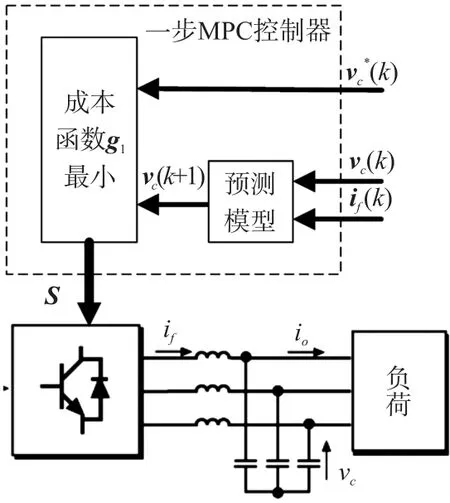
图3 一步预测MPC 控制框架

步骤1 测量采样时间k时输出电压vc(k)和滤波电流if(k)的值。

步骤2 使用式(14)预测逆变器生成的所有可能电压矢量的下一个采样时刻vc(k＋1)处的输出电压值，如表1 所示。

步骤3 利用预测vc(k＋1)值使用式(15)估计输出电流io(k)。

步骤4 使用成本函数g1对vc(k＋1)获得的7个预测值进行比较。

步骤5 然后选择使该函数最小的电压矢量vi，并在下一个采样时刻施加其相应的开关状态。

步骤6 等待到采样时间k＋1，返回到步骤1。

3 改进模型预测控制

当考虑两步骤进行预测时，将考虑两种情况的电压矢量。在第一种情况下，在第一采样周期内施加一个电压矢量，在第二采样周期内施加另一个电压矢量。这需要大量的计算，会使该算法的实验实现非常困难。第二种情况，在两个采样周期内施加相同的电压矢量以减少计算次数。这种方法可以简化算法运算步骤。并且在两种情况下，其优化性能都非常相似，并且比一步预测的性能更加优越[20]。因此，本文在两步骤进行预测时使用第二种情况。

对于输出LC 滤波器的三相逆变器，考虑两个预测步骤N＝2，改进后的MPC 框图如图4 所示。

图4 两步预测MPC 控制框架

改进后的MPC 在采样时间k处的控制步骤描述如下:

步骤1 测量采样时间k时输出电压vc(k)和滤波电流if(k)的值。

步骤2 考虑在当前采样间隔内转换器施加的电压，使用式(14)预测下一个采样时刻的输出电压vc(k＋1)和滤波器电流if(k＋1)的值。

步骤3 利用vc(k＋1)和if(k＋1)的值，预测逆变器产生的所有可能电压矢量的输出电压vc(k＋2)的值。

步骤4 使用成本函数g2比较7 个预测的vc(k＋2)值。

步骤5 然后选择使该函数最小的电压向量vi，并在下一个采样时刻k＋1 施加其相应的开关状态。

步骤6 使用式(15)估算用于预测k＋2 的输出电流io(k＋1)的值。在本文中，测量并馈送输出电流io(k)的当前值，以预测在下一次采样时的输出电压vc(k＋1)和滤波器电流if(k＋1)的值。

步骤7 等待到采样时间k＋1，返回到步骤1。

本节中逆变器在整个采样周期内施加电压矢量。提出的预测控制根据在时间k处进行的测量，并将新的电压矢量应用在时间k＋1 中，计算出时间k＋2 的预测值。

3.1 成本函数

最小化的成本函数评估输出电压预测值和参考电压之间的误差。在本文中，用正交坐标表示成本函数gN，并定义了系统的期望行为，以使输出电压的误差最小化。成本函数可表示为:

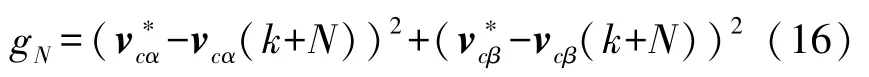
因此，针对一步预测步长N＝1，MPC 的成本函数可以表示为:

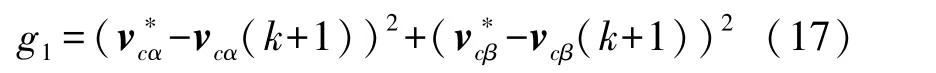
针对两步预测步长N＝2，改进MPC 的成本函数可以表示为:

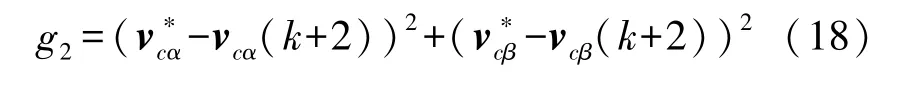
4 仿真实验分析

利用MATLAB/Simulink 工具对电阻性和非线性负载下的如图1 所示的系统进行了仿真，以验证所提出的三相逆变器控制策略。通过一步和两步预测对系统的性能进行评估和比较，根据UPS 实际工作状况和负荷情况选择参数如表2 所示[21]。

表2 系统参数

图5～图7 表示在电阻性负载为50 Ω、2 kΩ 和4 MΩ 时，MPC 在只有一个预测步骤的情况下的输出电压和电流。UPS 的输入电压范围在170 V～250 V之间，因此本文参考电压的幅值设置为200 V，频率为50 Hz。观察到稳态运行时输出电压呈低失真的正弦曲线。此外，达到稳态运行的时间随电阻性负载的变化而变化。在电阻负载为50 Ω、2 kΩ和4 MΩ 的情况下，达到稳定运行时间大约需要5 ms、10 ms 和10 ms，电压总谐波失真分别为2.30%、3.34%和3.48%。

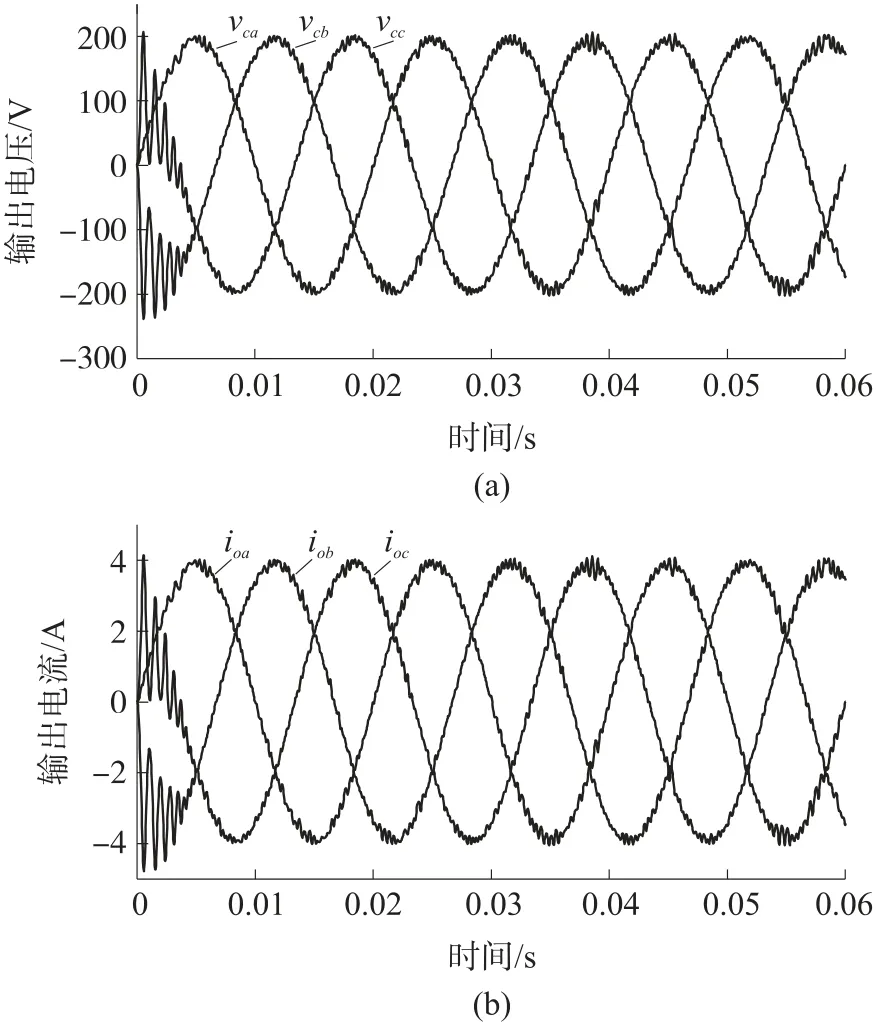
图5 50 Ω 负载一步MPC 控制的输出电压和电流

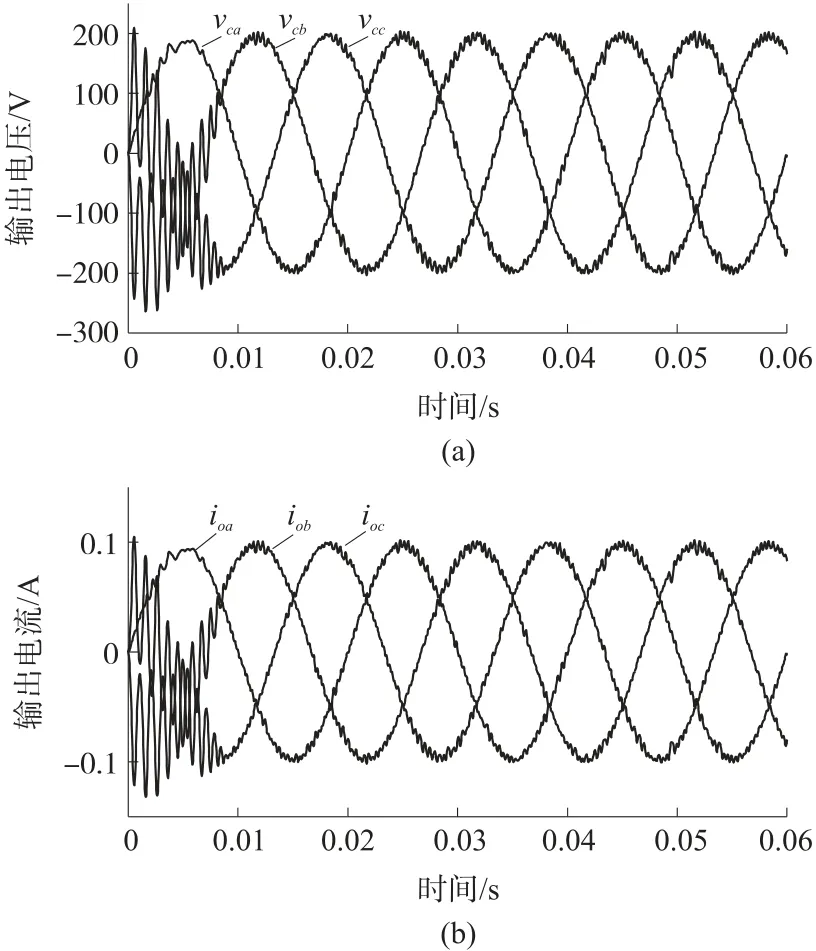
图6 2 kΩ 负载一步MPC 控制的输出电压和电流

图7 4 MΩ 负载一步MPC 控制的输出电压和电流

图8～图10 表示对于相同的电阻负载下，具有两个预测步骤的改进型MPC 的优化结果。可以观察到，在这些情况下，性能非常相似，并且比一步预测的输出电压和电流性能更加优越。三种电阻负载下输出电压THD 分别为0.94%、0.96%和0.97%，因此THD 可以认为是恒定的，其值约为0.96%，并且波形达到稳态的时间也是是恒定的，其值为2 ms。两种MPC 情况下不同阻性负载的仿真结果如表3所示。可以看出，在MPC 情况下，阻性负载值的变化会导致输出电压THD 的值和达到稳态时间的变化。与改进的MPC 不同，由于变化很小，THD 和达到稳态的时间可以认为是恒定的，并且比第一种情况要好。

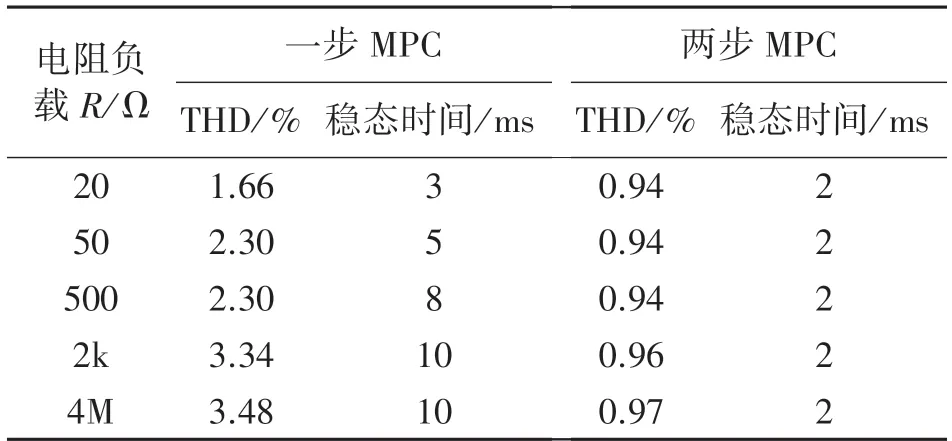
表3 不同负载下两种方法对比

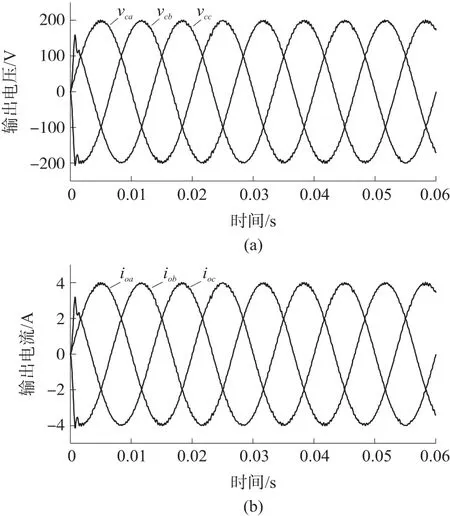
图8 50 Ω 负载两步MPC 控制的输出电压和电流

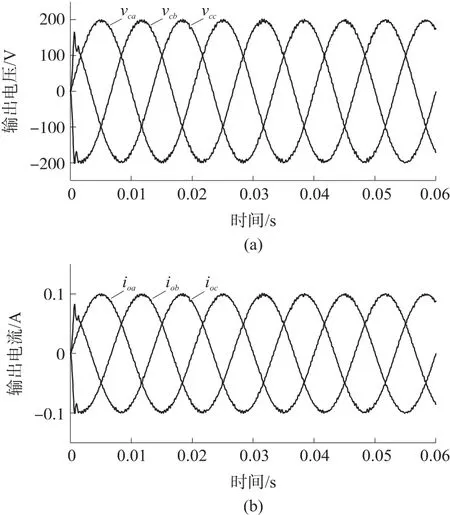
图9 2 kΩ 负载两步MPC 控制的输出电压和电流

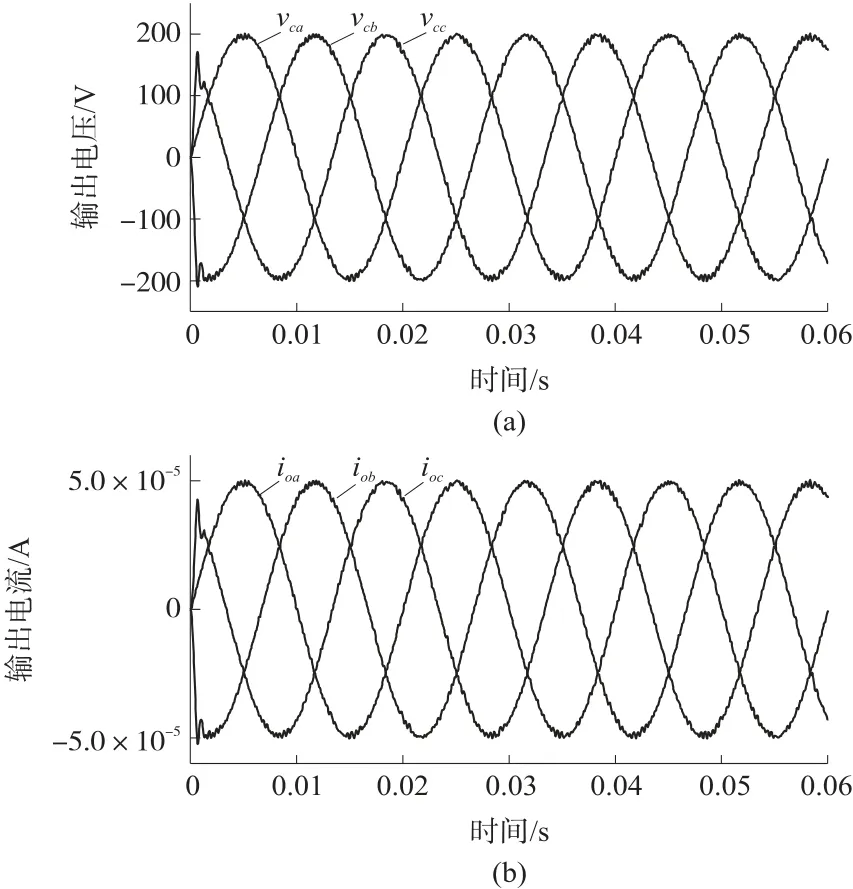
图10 4 MΩ 负载两步MPC 控制的输出电压和电流

本文使用二极管桥式整流器模拟非线性负载，本节设定两个案例。案例Ⅰ:R＝60 Ω，C＝3 000 μF；案例Ⅱ:R＝1 000 Ω，C＝3 000 μF。图11 表示仿真实验中非线性负载示意图。图12 和13 显示了非线性负载下一步MPC 的控制效果，可以看出尽管负载电流严重失真，但控制器的输出电压控制性能仍然良好，在仿真时间15 ms 之后电压波形正常，没有明显失真。此外，两种案例仿真下，系统输出电压达到稳态的时间基本相同，输出电压THD 分别为2.12%和2.24%。

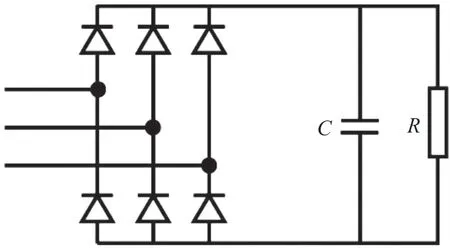
图11 非线性负载

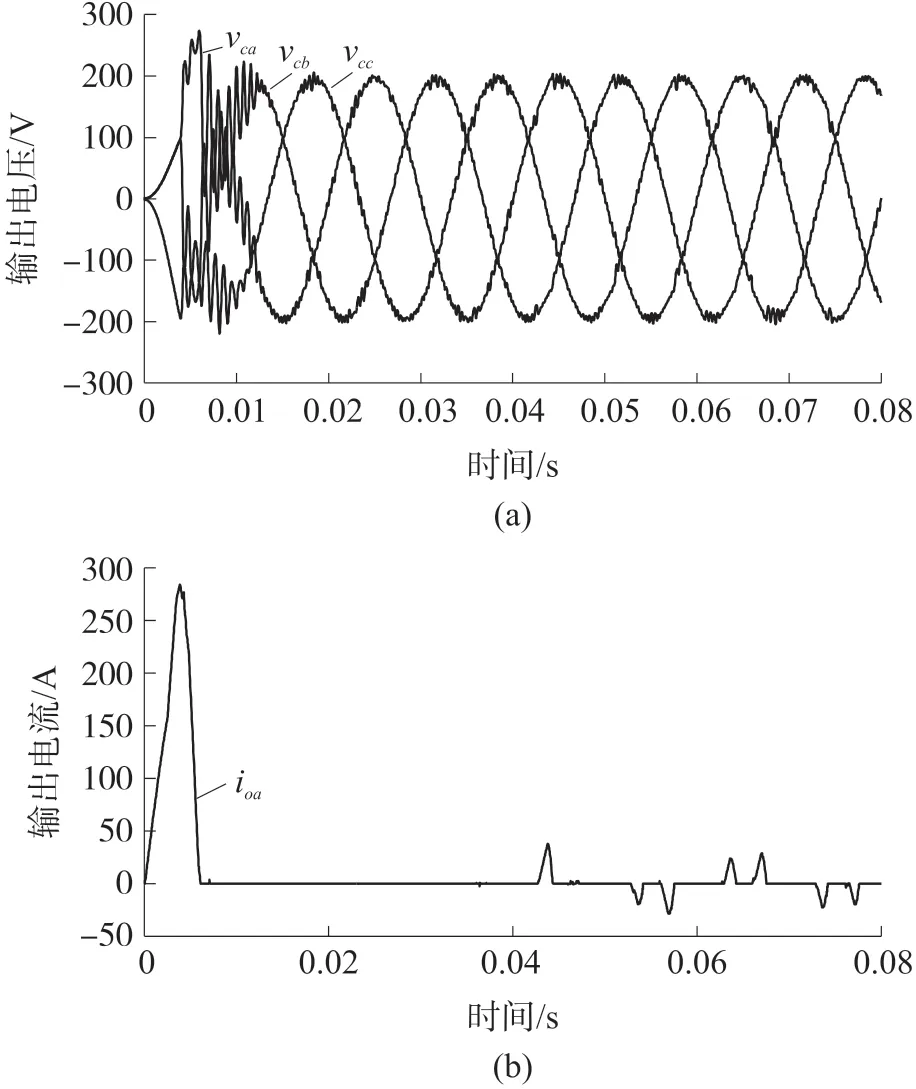
图12 案例Ⅰ一步MPC 控制的输出电压和电流

图13 案例Ⅱ一步MPC 控制的输出电压和电流

图14 和图15 表示改进的MPC 在相同的非线性负载下的输出电压和电流的控制效果。可以观察到，输出电压呈现出很小的失真，两个案例下输出电压THD 分别为1.04%和0.83%。此外，两种情况下的达到稳态时间均小于10 ms(小于0.5 个周期)。表4 表示在C＝3 000 μF 下不同电阻时两个方法控制效果对比，表5 表示在R＝60 Ω 下不同电容时两个方法控制效果对比。可以观察到，改进的MPC 的性能优于MPC，在输出电压控制上达到稳定的时间更短，电压THD 值更小。

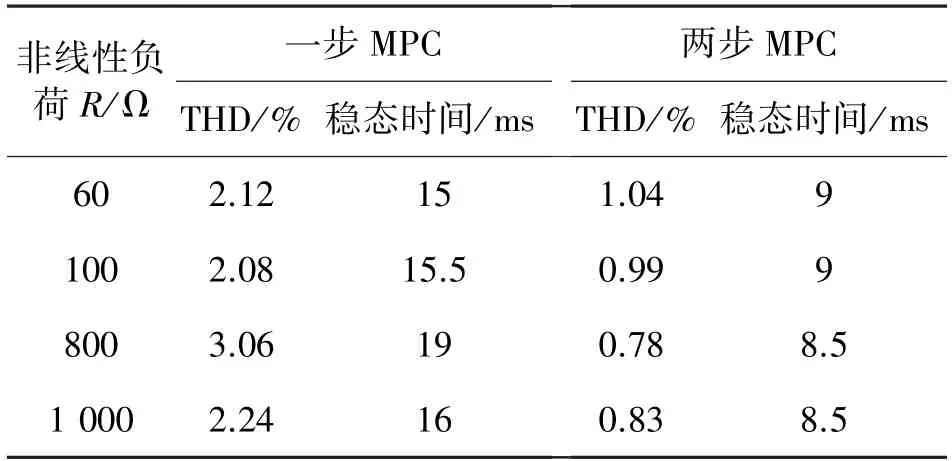
表4 不同电阻下控制效果对比

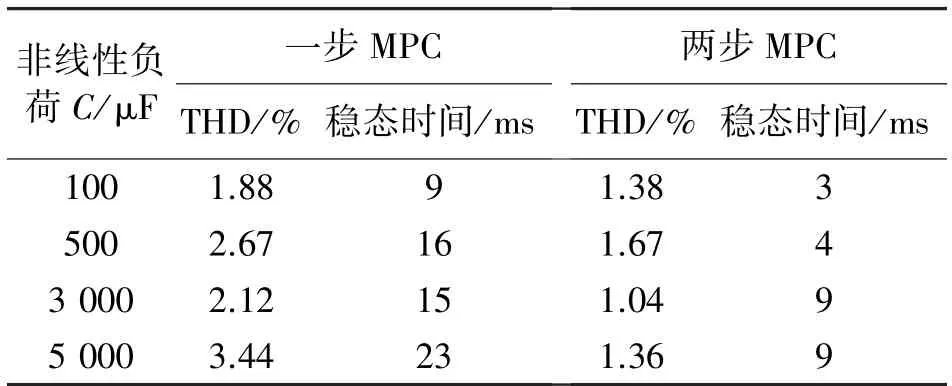
表5 不同电容下控制效果对比

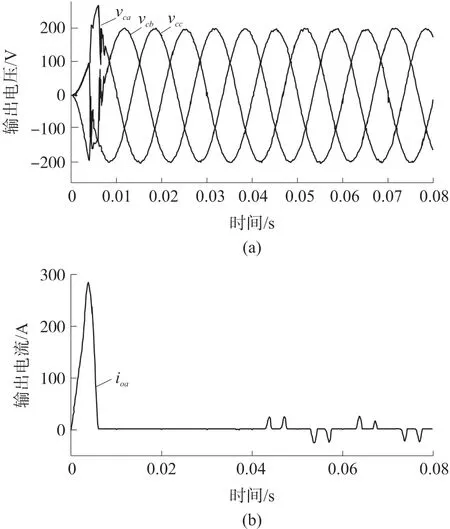
图14 案例Ⅰ两步MPC 控制的输出电压和电流

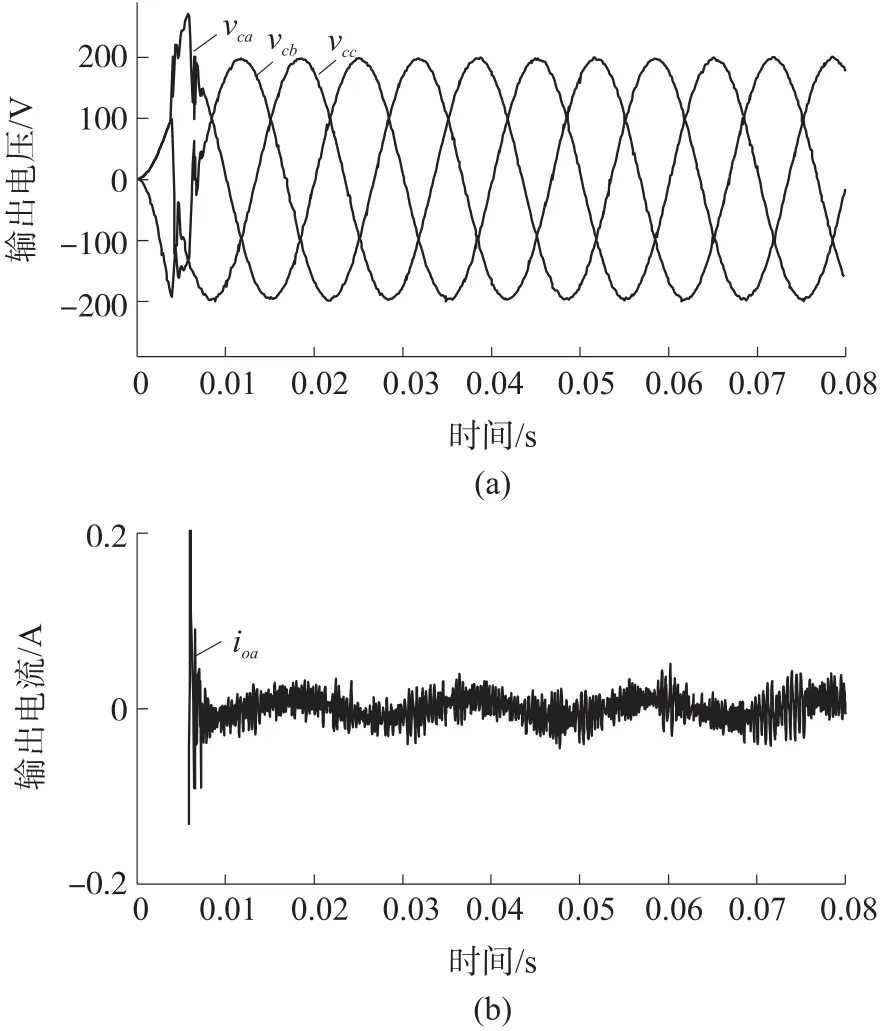
图15 案例Ⅱ两步MPC 控制的输出电压和电流

5 结论

本文提出了一种具有两个预测步骤的改进MPC 控制策略，通过在多个采样周期中施加相同的电压矢量进而简化多预测步骤计算量变大的问题，并将其与具有一个预测步骤的MPC 进行了比较。可以观察到，当考虑更多数量的预测步骤时，系统的行为会明显改善。仿真结果表明，对于一步MPC，不同的阻性负载值，阻性负载值的变化会导致输出电压THD 的值和稳态时间明显变化。而改进MPC的THD 和达到稳态时间由于变化很小，可以认为是恒定值，并且不会随电阻负载的不同而变化；对于非线性负载，改进的MPC 以较低的THD 和更少的时间实现输出电压的稳定控制。对于阻性负载和非线性负载，改进的两步MPC 均可以快速稳定地控制输出电压。