低插入损耗的8 GHz～18 GHz CMOS无源延时线设计∗

张 明，徐 琴

(1.成都职业技术学院软件学院，四川 成都 610041；2.重庆邮电大学移通学院，重庆 401520)

对于宽带相控阵系统等要求延时可控且工作频率较高的应用，基于无源二阶全通网络(APN)的延时模块[1－2]是较好的选择方案。与传统传输线延时结构相比，无源二阶APN 具有更高的延时带宽乘积[3]，且集成面积更小。这两个特性促使无源APN电路被广泛用于实现高频集成延时电路。

与无源APN 相比，有源二阶APN 的电路尺寸通常要小得多。例如，Mondal 等人[4]提出了一种全通滤波器架构的2 GHz 有源延时单元，采用了0.18 μm CMOS 工艺，延时范围为0.25 ns～1.7 ns。但是，有源二阶APN 的使用仅限于工作频率小于几个GHz 的应用。对于在高频宽带上的应用来说，无源二阶APN 的适用性更好。但是，单个无源二阶APN的延时带宽乘积有时不足以提供所需群延时值，因此研究人员提出将多个相同的无源二阶APN 进行级联。例如，Hu 等人[5]提出了一种0.13 μm 工艺1 GHz～20 GHz 延时电路，最大延时为400 ps，获得了较小的延时误差。Moallemi 等人[6]提出了一种用于相控阵天线的宽带可控延时模块。但是，在此类设计方法中，随着群延时的增加或上限频率的增加，需要更多的无源APN 电路，这就导致了更大的插入损耗和更大的电路尺寸。

因此，本文设计了一种利用较少的级联无源APN 实现高群延时的新方法。该方法利用二阶APN 群延时频率响应的峰值特性，从单个APN 电路中提取更多的群延时，适用于高频宽带通应用。该方法在实现大群延时的同时，具有插入损耗低、电路尺寸小的优点。该无源延时线设计采用0.18 μm CMOS 工艺进行了具体实现，可在8 GHz～18 GHz的频段内提供120 ps 的最大延时和3.9 ps 的最小延时，延时步长为3.9 ps。

1 群延时设计方法

1.1 传统方法

两种经典的无源二阶APN 电路[7－8]如图1 所示。

图1 两种经典的无源二阶APN 电路

在终端阻抗完全匹配的情况下，这些无源结构的散射参数S21如下所示:

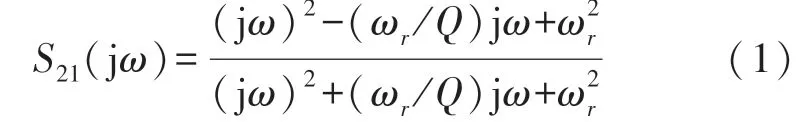
式中:ωr和Q均为设计参数，可确定APN 电路在频率上的群延时响应。利用奇偶模理论[9]，由电感寄生电阻引起的延时电路插入损耗可以根据如下方式计算:

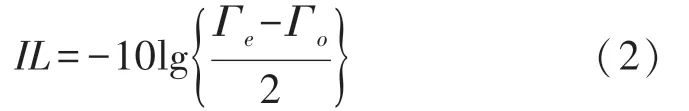
式中:Γe和Γo分别为偶模和奇模反射系数。以图1(a)为例，Γe和Γo的计算方式如下:

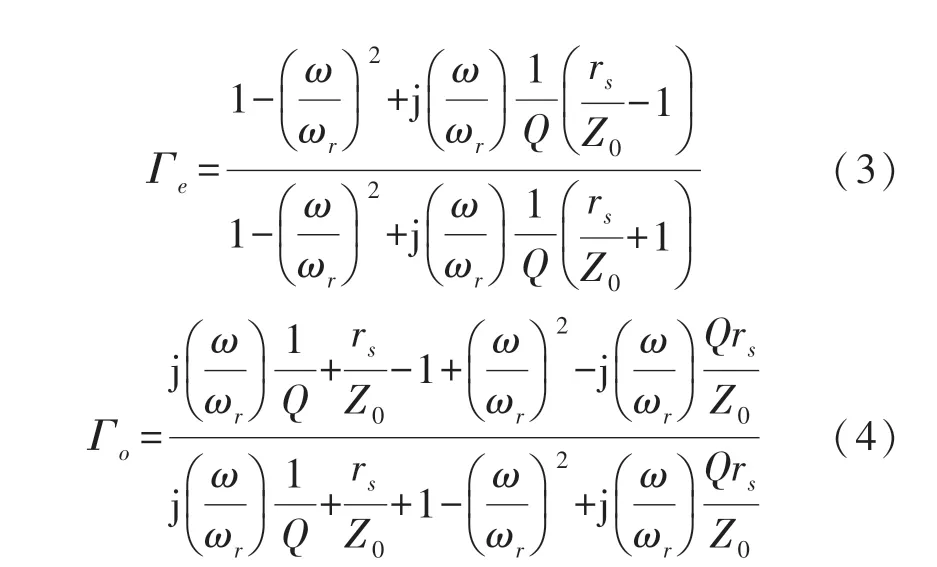
式中:rs为串联寄生电阻，Z0为参考阻抗(通常为50 Ω)。尽管单个无源二阶APN 电路的插入损耗值较小，但不能被忽略。

当单个二阶APN(Q＝)无法在特定频率间隔内提供所需的群延时，现有的解决方案是级联几个具有较低延时响应的APN 电路。受益于群延时累积，可达到较高的群延时响应。图2 显示了演示这种方法的示例。

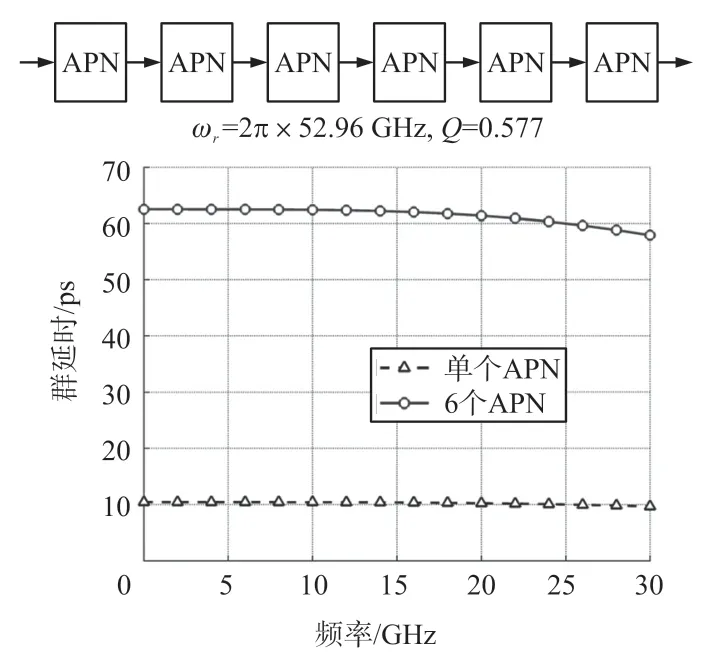
图2 传统级联实现8 GHz～18 GHz 的62.5 ps 延时

在本例中，通过级联六个二阶APN(每个具有10.41 ps 的延时)，在8 GHz～18 GHz 的带宽内实现了平坦的62.5 ps 延时响应。级联的方法相对简单直接。然而，随着群延时的增加或工作频率向更高的水平移动，将需要更多的二阶APN 电路。因此，会导致更大的面积和更高的损耗。

1.2 提出的群延时交错方法

如Ghazizadeh 等人[10]的研究所述，可以观察到Q值大于的二阶APN 群延时响应具有峰值特性。在几个二阶APN 电路的级联中，可以将每个模块设计为以交错方式在特定频率处具有峰值群延时，从而可以实现相对平坦的群延时响应。与所有APN 块都相似且Q＝的情况相比，该群延时会更高。这种新的设计方法可以称为群延时交错，可以在使用更少的无源二阶APN 电路的同时提供更大的群延时，并减小了插入损耗和电路面积。图3显示了采用所提方法的一个示例。在此示例中，仅使用两个二阶APN 模块，即可在8 GHz～18 GHz 带宽上获得62.5 ps 的群延时。

图3 所提方法实现8 GHz～18 GHz 的62.5 ps 延时

为了阐明这种新方法的优点，在相同的0.18 μm CMOS 工艺条件下，从电路大小和模拟插入损耗两个方面对图2 和图3 所示两种电路进行了比较。为了实现两个示例电路的二阶APN 模块，选择了图1(a)的电路结构。该延时结构的元件值如下所示:

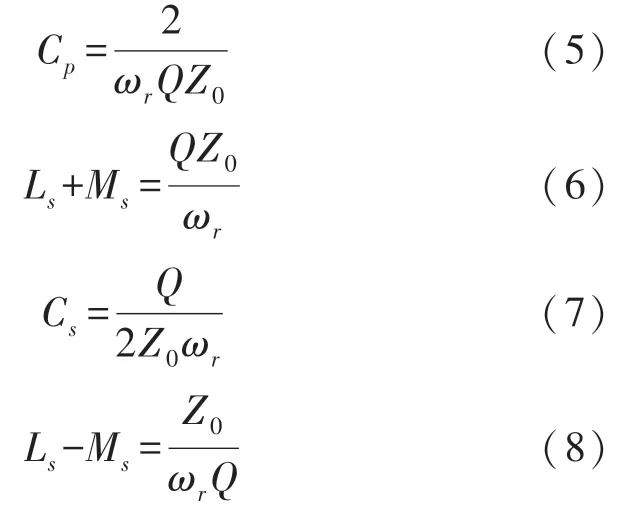
在CMOS 集成电路实现中，电感元件对电路尺寸有很大影响[11－13]，其相关的品质因数对电路的插入损耗值有很大影响。图2 所示延时电路需要六个173.56 pH 的耦合电感，耦合系数为－0.5。而图3 所示延迟电路仅需要两个721.35 pH 的耦合电感，耦合系数为－0.35。两种示例电路实现的版图如图4 所示。

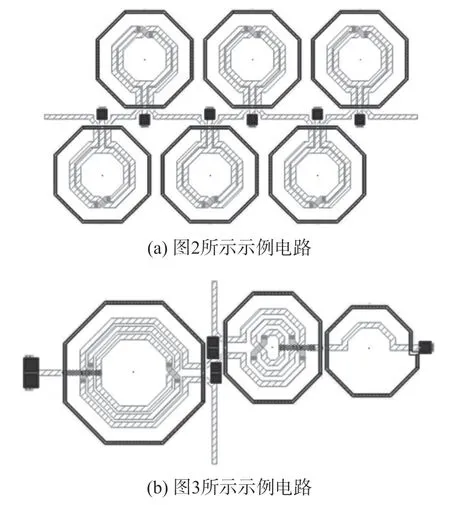
图4 两种示例电路的实现版图(0.18 μm CMOS)

图4(a)和图4(b)中延时电路的尺寸分别为0.24 mm2和0.17 mm2。因此，所提出的群延时设计方法可以得到更紧凑的电路。

对图4 所示的两个延时电路进行了电磁仿真。这两个电路的插入损耗仿真结果如图5 所示。

图5 插入损耗仿真结果

采用所提方法的电路由于电感元件的数量较少而具有较小的损耗。相比传统级联电路，在18 GHz时，损耗降低了约1.1 dB。在使用新设计方法时，以更多的群延时偏差为代价，获得了更低的插入损耗和更小的电路尺寸。图6 显示了图4 中两个示例电路在8 GHz～18 GHz 频带上的群延时曲线。

图6 群延时仿真结果

在上述带宽内，两个延时电路的平均群延时均为62.5 ps。然而，该设计方法实现的电路最大群延时偏差比平均值高0.75 ps，而传统级联方法实现的电路最大群延时偏差仅为0.2 ps。

2 实验结果与分析

2.1 集成无源延时线电路

采用0.18 μm CMOS 工艺设计并实现了一种5 bit延迟控制的集成延时线电路。工作频率带宽的目标是覆盖8 GHz～18 GHz。这个可变延时电路的框图如图7 所示。

图7 5 bit 延迟控制的集成延时线电路框图

该集成电路包含五个无源可控延时模块，设计的群延时为3.9 ps、7.8 ps、15.6 ps、31.25 和62.5 ps。因此，集成延时线可以提供最大125 ps 的延时，延时分辨率为3.9 ps。简单的匹配网络被放置在射频路径的起点和终点[14－16]，以减少输入/输出焊盘寄生电容的失配效应。延迟模块的放置顺序是通过最大程度地减少相邻模块对彼此群延时响应的不利负载影响来确定的。

2.2 测量结果

制作的延迟线电路芯片显微照片如图8 所示，其总面积(包括射频焊盘)为1.2 mm×2.7 mm。在片上进行了测量，并使用安捷伦网络分析仪E5071C测量了S参数结果。

图8 无源延迟线电路芯片显微照片

群延时结果是通过测量相变数据并对频率进行推导而获得的。为了最小化群延时提取过程中的噪声污染，需要考虑几个因素。首先，采样频率点的数量被选择为401 个，对应于相对较小的35 MHz 频率步进。此外，为了降低噪声水平，测量网络分析仪的中频带宽分辨率已降至相对较小的30 kHz[17－18]。其次，在数据采集后，对测量的相位数据进行数字滤波，去除高频噪声干扰，得到平滑的群延时曲线。5 bit无源延时线的群延时如图9 所示。

图9 中31 个延时对应的均方根群延时误差如图10 所示。

从图9 和图10 可以看出，制作的延时线电路芯片在8 GHz～18 GHz 带宽内平均最大群延时为120 ps，最坏情况下的均方根误差小于3.3 ps。

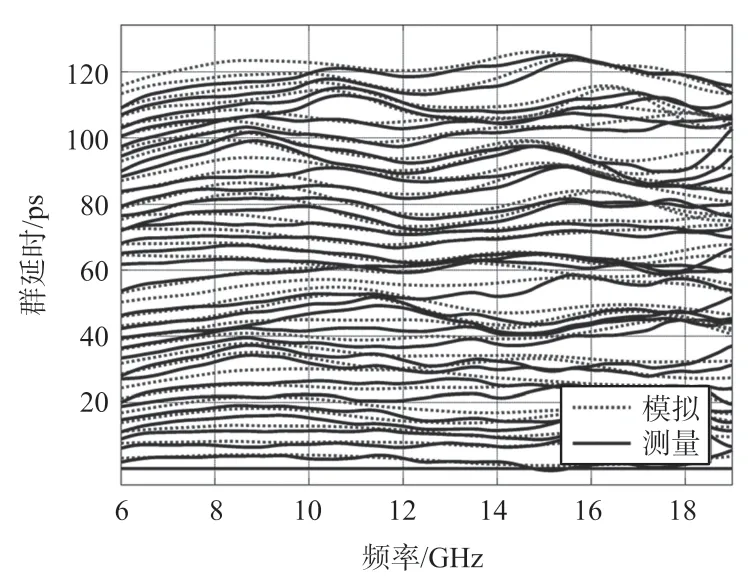
图9 5 bit 无源延时线的群延时

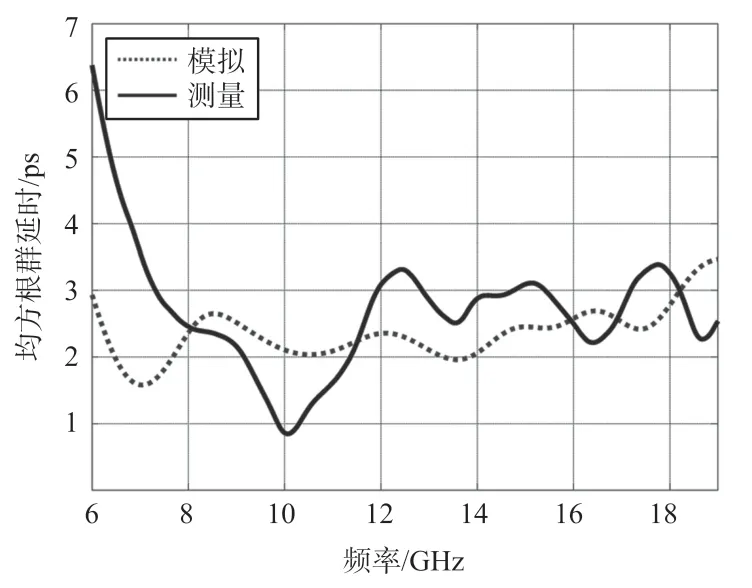
图10 均方根群延时误差

所制造的延时线在其工作带宽上具有令人满意的输入和输出反射系数，分别如图11 和图12 所示。

图11 输入反射系数

图12 输出反射系数

所制造的5 bit 延时线的插入损耗如图13所示。

从图13 可以看出，插入损耗从8 GHz 时的12.6 dB(平均值)增加到18 GHz 时的20.5 dB(平均值)。在工作频带的较高端，测得的插入损耗比模拟结果大约高1.4 dB。这一额外损耗可能是在较高频率下测量的反射系数比模拟值低的原因。最大插入损耗变化出现在17.7 GHz，约为±2.1 dB。

图13 插入损耗

将所提无源延时线电路芯片与现有相关工作进行了比较，如表1 所示。幅度误差表示整个延迟状态下插入损耗的变化，被定义为插入损耗的最大值减去平均插入损耗值(以分贝为单位)。

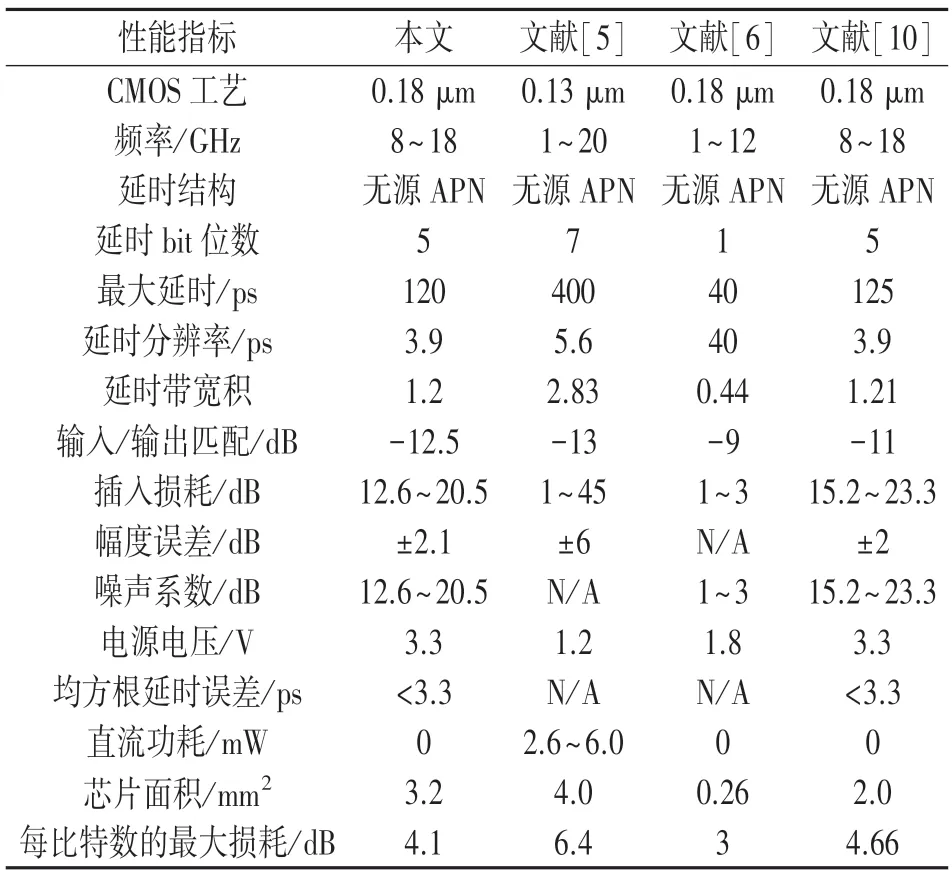
表1 可控集成延迟线的性能比较

从表1 可以看出，所提无源延时线具有中等的延时带宽积和幅度误差值。由于延时电路的控制位数相近且工作频率范围大致相同，重点将所设计的延时电路的插入损耗值与文献[10]中提出的延时电路的插入损耗值进行了比较。与文献[10]相比，所提延时线的插入损耗显著降低，特别是在更高的频率下。这一改进从表1 最后一行所示每比特数的最大损耗值中也得到验证。这表明，从较少的无源二阶APN 电路中获取较大的群延时有利于降低插入损耗。

3 结论

本文提出了一种新的群延时设计方法。该方法对二阶APN 群延时频率响应中的峰值特性进行了控制，从而获得相对较高的群延时值。因此，仅需较少数量的二阶APN 就可维持较高的群延时。采用0.18 μm CMOS 技术设计和制造了具有5 bit 控制位的无源集成延时线，在8 GHz～18 GHz 的频率间隔内获得了120 ps 最大延时，3.9 ps 延时分辨率。测试结果表明，所提延时线的均方根群延时误差小于3.3 ps，且平均插入损耗为12.5 dB～20.5 dB。与现有集成延时线相比，所提延时线电路芯片的插入损耗更低。