基于java实现的输电线路弧垂测量策略

蒋峰景， 吴 翔， 吴 睿， 凌 劲， 刘胜杰

(国网安徽省电力有限公司检修分公司， 安徽 合肥 231131)

0 引言

随着经济快速发展，人们对电能的需求不断增长，线路输送容量不断增大，保证输电线路的安全稳定运行显得尤为重要，而线路弧垂是输电线路安全运行的重要指标，在输电线路架线过程中，需要开展弧垂测量，以满足设计要求；在输电线路提高输送容量过程中，动态增容技术是其实现的重要手段，而线路弧垂决定了该技术的上限；在输电线路融冰过程中，直流融冰技术应用最为广泛，而线路弧垂影响着施加的直流电压的大小。因此，开展输电线路弧垂测量研究十分必要。

国内外对输电线路弧垂测量开展了许多针对性的研究，取得了丰硕的成果。目前弧垂观测的方法有等长法、异长法、角度法和平视法[1-3]。在进行测量时，为避免档距、悬挂点高差在测量时的影响，减少现场计算量以及掌握弧垂的实际误差范围，应首先选用异长法和等长法。当客观条件受到限制，不能采用异长法和等长法观测时，可选用角度法进行观测。如果某些地区地形复杂，杆塔间高差大，弧垂高于较低的杆塔，异长法、等长法和角度法均不能达到观测弧垂的允许范围且难以掌握实际观测误差，可以考虑用平视法来观测导线的弧垂。但这些方法不能满足现场生产的全部需要，为进一步弥补现场生产瓶颈，提出了一种在档外视野范围内测量弧垂的新策略，可称为“两点法”。该方法只需两导线悬挂点在视野范围内，不受地形、线路运行情况及线路台账等条件限制，且具有易操作、易实现、结果准确等特点，非常适合现场应用。

1 弧垂测量实现策略

“两点法”实现的弧垂测量，具体是先选取任意两基准点作为两经纬仪的摆放位置，确定两经纬仪间的距离，经纬仪对中，整平后，测量两基准点距离及基准点与导线悬挂点间的水平角及倾角，推导算出最大弧垂位置的水平偏转角；然后调节经纬仪水平偏转该角度，调节目镜，找到最大弧垂点，测量其仰角，最后推出最大弧垂计算公式；针对传统计算方法效率低的缺点，考虑运用java语言编写计算程序，录入观测参数即可迅速而准确地计算弧垂。该方法适用于前期资料收集、线路资料设计值与实际情况有出入、融冰线路或者现场情况不明条件下的测量，测量工作人员仅需携带经纬仪、皮尺或卷尺、电脑即可一人在现场完成所有测量工作，操作简单，在工程上具有极强的推广应用价值。

具体操作和分析如下：

(1)在线路附近，视野范围内找到合适的两基准点z1、z2，用皮尺或卷尺测量两基准点间的距离l。

(2)将两台经纬仪安放在两基准点z1、z2上，对中、整平后，测量两基准点与导线悬挂点间的水平角及倾角，为方便分析，在适当位置建立空间直角坐标系，如图1所示。

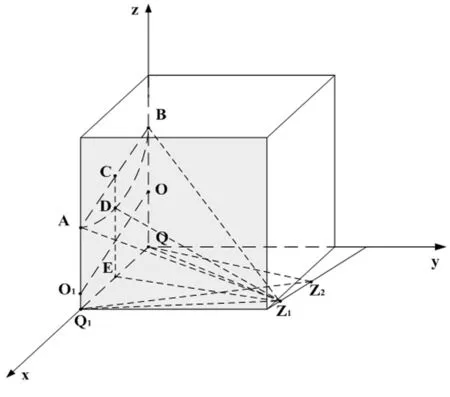
图1 两点法弧垂测量示意图

图1中：|AQ1|为基塔A距离地面的距离；|BO|为基塔B距离地面的距离；Z1、Z2为两台经纬仪安放位置；D点为基塔A、B水平距离中点垂线与导线交点；Q、Q1分别为Z1、Z2所在平面与直线AQ1、直线BO的交点；C、E分别为AB、QQ1中点。

1)先通过经纬仪测量水平角∠Q1Z1Z2、∠Q1Z2Z1、仰角∠AZ1Q1，设其分别为∂1、∂2、θ1；计算Z1点距离基塔A的水平距离|Q1Z1|和基塔A距离Z1、Z2点所在水平面的距离|AQ1|；计算如下。

在ΔQ1Z1Z2中，由三角形边长定理可得到公式(1)：

(1)

式(1)中，|Q1Z1|为Z1点距离基塔A的水平距离、l为两基准点Z1、Z2间的距离，∂1、∂2、θ1分别为经纬仪测量得到的水平角∠Q1Z1Z2、∠Q1Z2Z1、仰角∠AZ1Q1的大小。

在ΔAQ1Z1中，由三角形边长定理也可得到公式(2)：

(2)

式(2)中， |AQ1|为A点到Q1点的距离， |Q1Z1|为Q1点到Z1点间的距离，l为两基准点Z1、Z2间的距离， ∂1、∂2、θ1分别为经纬仪测量得到的水平角∠Q1Z1Z2、 ∠Q1Z2Z1、仰角∠AZ1Q1的大小。

2)同理，再通过经纬仪测量水平角∠QZ1Z2、∠QZ2Z1、仰角∠BZ1Q，设其分别为γ1、γ2、θ1；计算Z1点距离基塔B的水平距离|QZ1|和基塔B距离Z1、Z2点所在水平面的距离|BQ|，易得到公式(3)、公式(4)：

(3)

式(3)中，|QZ1|为Z1点距离基塔B的水平距离，l为两基准点Z1、Z2间的距离γ1，γ2、θ2分别为经纬仪测量的水平角∠QZ1Z2、∠QZ2Z1。

(4)

式(4)中，|BQ|为B点到Q点的距离，|QZ1|为Q点到点Z1的距离；γ1、γ2、θ2分别为经纬仪测量的水平角∠QZ1Z2、∠QZ2Z1、仰角∠BZ1Q。

3)计算基塔A、B档距|QQ1|，由余弦定理可得到公式(5)：

(5)

式(5)中，|QQ1|为Q点到Q1点的距离，|Q1Z1|为Q1点到Z1点的距离，|QZ1|为Q点到Z1点的距离，∂1为经纬仪测量得到的水平角∠QZ1Z2，γ1为经纬仪测量的水平角∠QZ1Z2。

(3)找到两杆塔水平距离中点垂线与导线交点D，测量其仰角∠DZ1E，令∠DZ1E=μ1，具体分析如下。

1)先推导出偏转角度∠Q1Z1E，可令∠Q1Z1E1=φ，计算如下。

先令∠QQ1Z=δ，在中∠QQ1Z1，可得到公式(6)：

(6)

式(6)中，δ为∠QQ1Z1的大小，|Q1Q|为Q点到Q1点的距离，|Q1Z1|为Q1点到Z1点的距离，|QZ1|为Q点到Z1点的距离。

在ΔQQ1E中，可得到公式(7)：

(7)

式(7)中，|EZ1|为E点到Z1点的距离，|Q1Q|为Q点到Q1点的距离，|Q1Z1|为Q1点到Z1点的距离，δ为∠QQ1Z1的大小。

在ΔQ1Z1E中,可得到公式(8):

(8)

式(8)中，φ为偏转角度∠Q1Z1E的大小，|Q1Z1|为Q1点到Z1点的距离，|EZ1|为E点到Z1点的距离，|QQ1|为Q点到Q1点的距离。

2)以Z1与基塔A水平方向为基准线，即直线Z1Q1，将Z1点经纬仪向导线中间位置水平偏转角度φ。

3)调整目镜，找到D点，测仰角∠DZ1E，令∠DZ1E=μ1。

4)计算最大弧垂f，可得到公式(9)：

(9)

式(9)中，f为导线最大弧垂，μ1为仰角∠DZ1E的大小,|AQ1|为A点到Q1点的距离,|BQ|为B点到Q点的距离,|EZ1|为E点到点Z1的距离。

上述操作中也可只使用一台经纬仪，但需要来回移动经纬仪位置到Z1、Z2点。

2 java程序实现

开展弧垂计算时若通过传统计算方法计算，效率低且容易出错，本文利用java语言编写计算程序，录入观测参数即可迅速而准确地计算弧垂。其主程序编写如下：

public class Calculate

{

double Q1Z1,QZ1,EZ1,QQ1;

public Calculate(double l,double alpha1,double alpha2,double gamma1,double gamma2)

{

double sinr1r2,sing1g2;

sinr1r2=Math.sin((alpha1+alpha2)*Math.PI/180);

sing1g2=Math.sin((gamma1+gamma2)*Math.PI/180);

Q1Z1=l*Math.sin(alpha2*Math.PI/180)/sinr1r2;

QZ1=l*Math.sin(gamma2*Math.PI/180)/sing1g2;

QQ1=Math.sqrt(Q1Z1*Q1Z1+QZ1*QZ1-2*Q1Z1*QZ1*Math.cos((alpha1-gamma1)*Math.PI/180));

double COSTHETA=(QQ1*QQ1+Q1Z1*Q1Z1-QZ1*QZ1)/(2*Q1Z1*QQ1);

EZ1=Math.sqrt((1.0/4)*QQ1*QQ1+Q1Z1*Q1Z1-QQ1*Q1Z1*COSTHETA);

}

public String Calculate2()

{

doublephi=180.0/PI*Math.acos((Q1Z1*Q1Z1+EZ1*EZ1-(1.0/4)*QQ1*QQ1)/(2*Q1Z1*EZ1));

String out1=String.format("%.2f", phi);

return out1;

}

public String Calculate3(double theta1,double theta2,double mu)

{

double AQ1,BQ,DE;

AQ1=Q1Z1*Math.tan(theta1*Math.PI/180);

BQ=QZ1*Math.tan(theta2*Math.PI/180);

DE=EZ1*Math.tan(mu*Math.PI/180);

doubleff=(1.0/2)*(AQ1+BQ)-DE;

String out1=String.format("%.5f", ff);

return out1;

}

}

计算界面如图2所示。

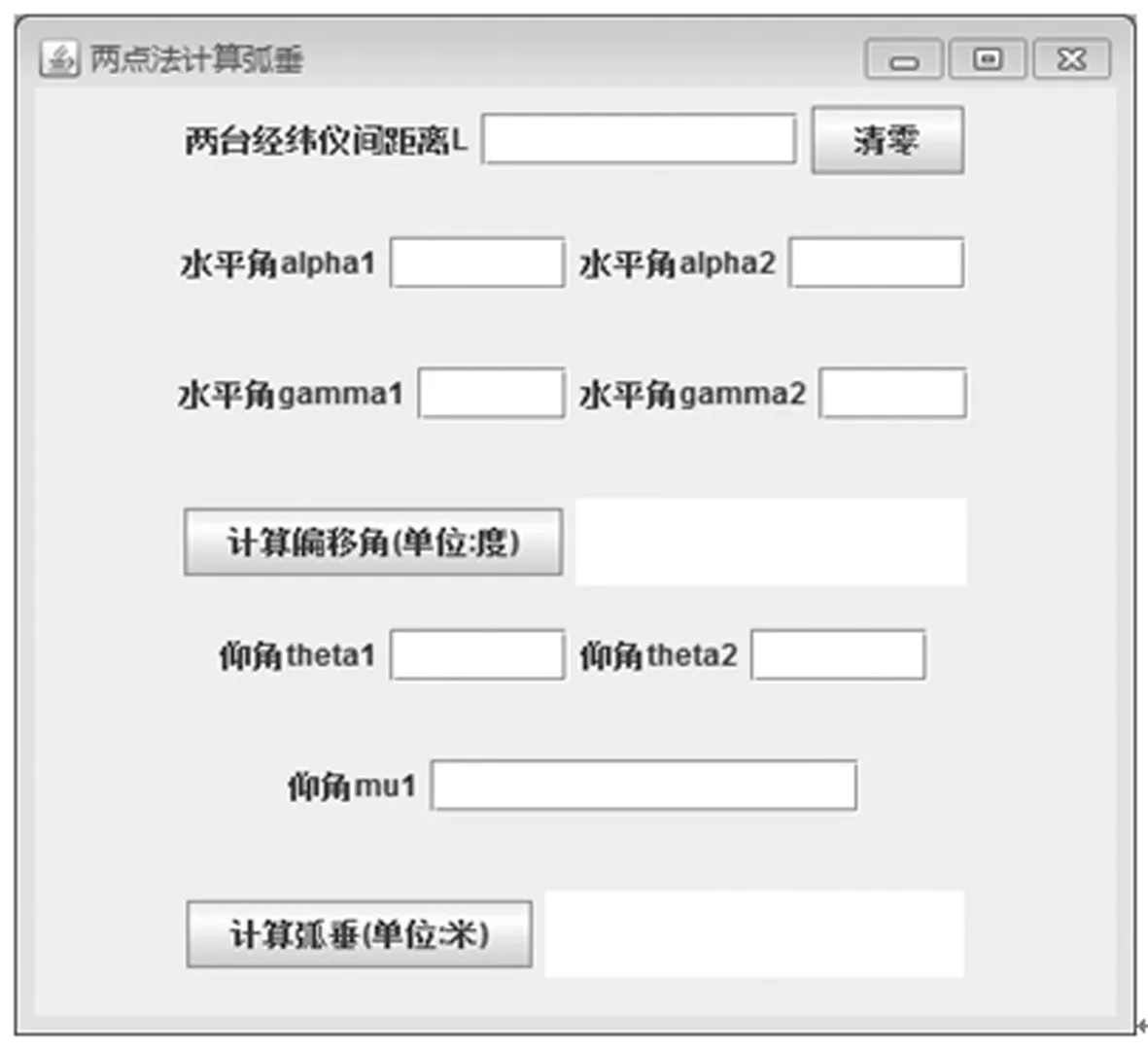
图2 “两点法”java计算界面

3 应用案例

为验证该策略的正确性，文中对某500 kV输电线路开展弧垂测量。选取其中2个区段测量弧垂大小，测量结果与设计理论值对比进行分析。分析如下。

选取某区段1，查阅资料其设计的弧垂大小为3.10 m，利用本文中的方法开展测量，输入测量的参数结果如图3所示。

图3中，依据本文测量方法，弧垂计算结果为3.193 35 m，误差大小为3%，考虑测量误差及导线的热胀冷缩，可认定误差在合理范围内，且测量结果较为准确。

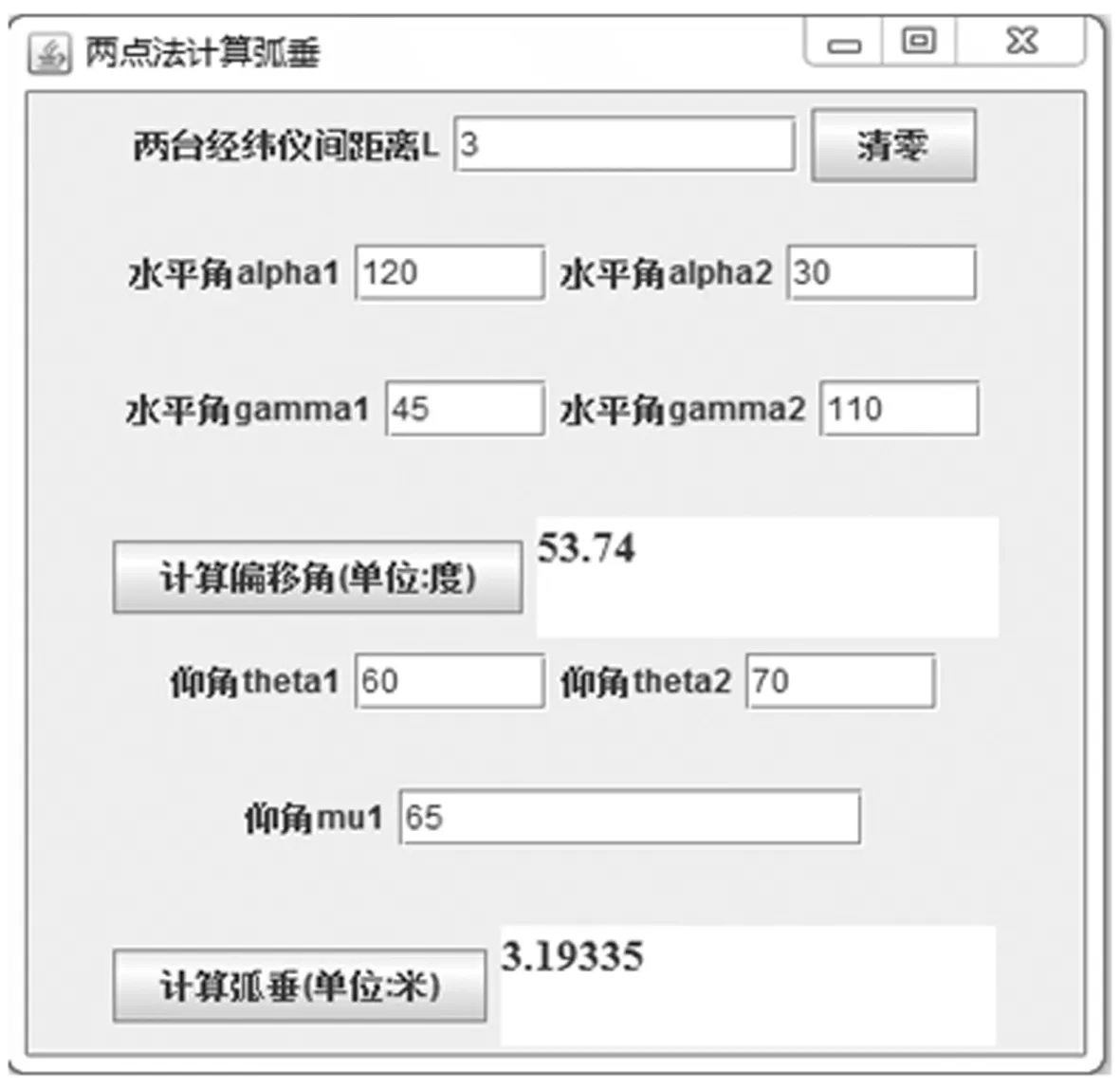
图3 某500 kV输电线路区段1弧垂测量结果

选取某区段2，查阅资料其设计的弧垂大小为3.3 m，利用本文中的方法开展测量，输入测量的参数结果如图4所示。

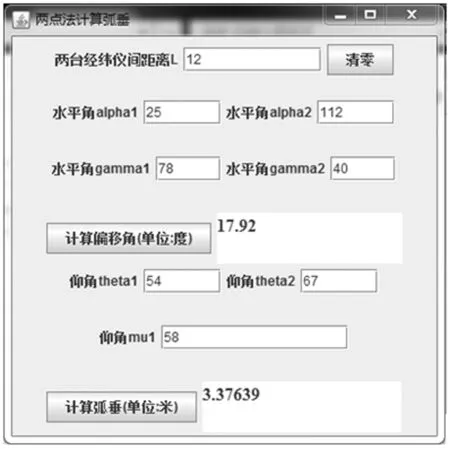
图4 某500 kV输电线路区段2弧垂测量结果

图4中，依据本文测量方法，弧垂计算结果为3.376 39 m，误差大小为2%，考虑测量误差及导线的热胀冷缩，可认定误差在合理范围内，且测量结果较为准确。

综上所述，基于java实现的输电线路弧垂测量策略能够快速、准确地实现对输电线路弧垂的测量。

4 结束语

一种基于Java实现的输电线路弧垂测量策略，通过经纬仪测量参数录入计算程序，快速得到最大弧垂，在工程上具有极强的推广应用价值。但在选择基准点时，为减小误差，我们应尽量选择同一水平面上的两点，且在基准点均能用经纬仪观测到导线两端悬挂点。