基于双目视觉的空中加油锥套定位与对接控制

张易明, 艾剑良

(复旦大学航空航天系, 上海 200433)

0 引 言

空中加油是一种增加无人作战飞机作战半径的主要方法,可分为软管-锥套式(软式)、伸缩套管式(硬式)两类[1]。其中,采用软式加油系统进行空中加油具有加油装置体积小、结构简单、便于拆装、可在一台加油机上安装数套装备等优势[2],有广阔的应用前景。空中加油过程包括会合、编队、对接、加油和退出5个阶段,对软式自主空中加油而言,对接阶段对控制的要求最高[3]。在软式加油过程中,加油锥套在加油机尾涡下洗及大气紊流作用下处于持续运动中[4],其摆动范围可达到2 m[5]。因此,快速准确地定位锥套位置,是实现自主精确对接控制的前提条件。

在对接过程中,受油机从加油机侧后方锁定加油锥套并逐渐靠近。在这个区域,由于多种干扰影响,传统惯性导航与GPS组合的导航方法难以提供高精度的位置测量信息[6],而使用雷达系统难以从加油机-加油装置组合体中分辨出加油锥套的位置。因此,基于视觉技术的测量方法是具有应用潜力的方案之一。近年来,相继出现了一些基于Mean-Shift和卡尔曼滤波及其改进或结合形式的单目锥套检测方法[7-12],用于从摄像机拍摄到的图像中寻找加油锥套。在对接过程中,仅在相机视野中识别出加油锥套是不够的,还需通过测量锥套在视场中的深度解算其空间位置。文献[13-14]开展了基于双目视觉的加油锥套定位研究,文献[15-17]研究了基于深度学习的锥套定位方法。对于双目立体视觉问题,传统的方法是先在一侧画面中提取感兴趣的点或区域,利用色彩/灰度匹配边缘匹配等方法在另一侧画面中找到共轭点对,随后通过对极几何求解空间点的坐标信息[18]。此种方法计算量大,难以满足实时性要求。考虑到加油锥套在受油机视野中的几何形态相对简单且固定,可利用基于深度学习的目标检测网络分别在两侧画面中定位其中心位置,再利用对极几何求解其空间坐标,可加快对加油锥套定位的速度。

对于图像中锥套目标的检测问题,多数研究是基于色彩信息的滤波跟踪方法,需要在加油锥套上额外加装彩色光源以区分前景与背景,并要求加油锥套在受油机视野中呈现完整的椭圆形。当跟踪目标与背景颜色接近或被遮挡时,容易出现跟踪窗口扩大等问题;同时,此类方法对初始帧中目标所在位置的估计有较大依赖。为克服以上问题,可以引入深度学习网络用于图像中的目标检测。YOLO(you look only once)系列是一种高速的目标检测网络[18-22],它的优势是兼顾了推理精度和速度,可作为目标检测阶段的一种选择。

在可获得锥套空间坐标的前提下,自主空中加油的对接控制问题可分为三部分:指令项、跟踪项、镇定项。指令项即指从编队位置到对接位置的参考轨迹设计。通常参考轨迹被设计为一条平滑轨迹,以避免过度的超调和震荡。现有的研究主要采用低通滤波器[23]、多项式[24]等方法生成参考轨迹等方法。跟踪项(外环)使受油机按照指定的参考轨迹完成对接任务,一般可以构建误差系统将跟踪问题转换为镇定问题。常见的方法有:非零点集方法(non-zero setpoint,NZSP),该方法将参考输出转化为参考状态[25];随后有学者提出指令生成跟踪器方法(command generator tracker,CGT),以克服NZSP需要常值参考输出的缺点[26]。镇定项(内环)用以保证系统稳定和收敛,基于比例-积分-微分(proportion integral derivative,PID)[27]和线性二次型调节器(linear quadratic regulator,LQR)[28-29]的控制器是比较常见的方法,亦有学者开展了基于自适应控制[30]、反步法[31-33]的对接控制研究。

1 问题描述

在空中加油对接阶段,受油机起始位置一般位于加油锥套侧后方偏下位置。以受油机机体系为参考坐标系,定义加油锥套中心相对受油机的位置矢量为rd=(xd,yd,zd),如图1所示。完成自主对接控制的任务即可分解为:第一,实时获得锥套位置rd;第二,使rd在一定时间内趋于0。

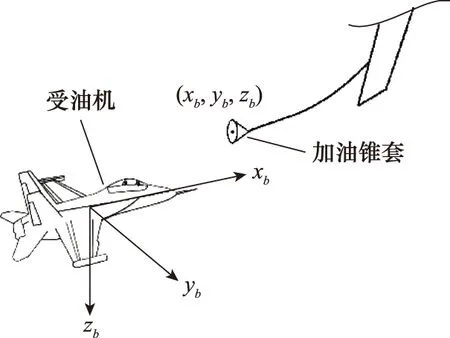
图1 受油机机体坐标系Fig.1 Body-axes of receiver aircraft

为实现上述目标,实现自主对接的任务流程可归结如下。

步骤 1利用计算机视觉方法获得rd:

(1) 在相机成像画面中检测加油锥套所在位置;

(2) 利用相机成像的映射关系反推加油锥套的空间位置rd。

步骤 2规划一条平滑的参考轨迹,在指定时间内逐渐消除rd。

步骤 3设计控制率使受油机跟踪参考轨迹以完成对接任务。

2 基于双目视觉系统的锥套定位

在受油机上架设双目相机后,在机体系内获得rd的问题转化为求取锥套在相机系统内的空间坐标问题。在实际应用中,单个相机捕获的是二维图像。因此,需求解空间点与相机成像画面点间的映射关系,进而获得加油锥套的空间坐标。

2.1 相机成像模型

相机成像过程涉及如下坐标系:

世界坐标系Ow-xwywzw,描述相机及被摄物体在真实物理空间中的位置,其原点和坐标轴方向可以任意指定,单位为mm;

相机坐标系Oc-xcyczc,其原点位于镜头光学中心,xc,yc轴与成像画面的两条边平行,zc轴与镜头光轴重合,单位为mm;

像素坐标系Opix-xpixypix,原点为成像画面左上角,xpix,ypix轴分别与成像画面的两条边平行,该坐标系反应成像画面中每一个像素点的行、列位置,坐标值均为非零正整数,单位为pixel。

图像坐标系Oimg-ximgyimg,原点为成像平面中心,ximg、yimg轴分别与成像画面的两条边平行,单位通常与世界坐标系一致。图像坐标系是对像素坐标系的物理性补充,便于参与相机坐标系及世界坐标系间的坐标变换。以上坐标系间关系如图2所示。

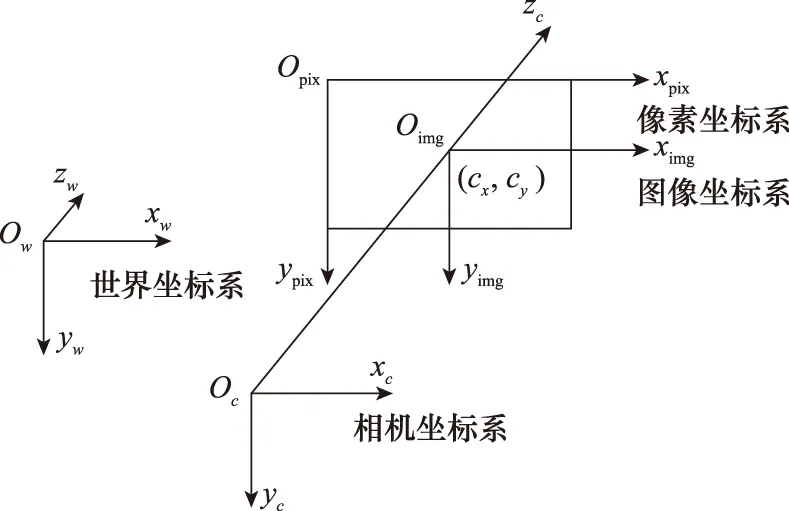
图2 世界、相机、图像和像素坐标系Fig.2 World, camera, image and pixel coordinates

相机成像模型可表示为

(1)

式中:KInt为内部参数矩阵;MExt为外部参数矩阵;zc称为尺度因子。具体表示为

(2)

式中:fx,fy分别为x、y方向对应的等效焦距,其定义是物理焦距与单位像素宽度的比值,单位为pixel;(cx,cy)为Oimg在Opix-xpixypix系下的坐标。

KExt=[R,t]

(3)

式中:R为3×3正交旋转矩阵;t为3×1平移向量。

实际的相机成像过程还需考虑镜头畸变,数学表达为

(4)

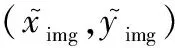
式(1)～式(4)描述了空间点(xw,yw,zw)到像素平面成像点(xpix,ypix)的映射关系,求解KInt、MExt、k、p的过程称为相机标定,可使用张正友标定法进行相机的参数标定[34]。张正友标定法是一种通过匹配棋盘格图像上角点的真实坐标与其成像坐标来求解成像映射关系的方法,主要步骤为[35]。

步骤 1令zw=0平面与棋盘格平面重合,构造单应性矩阵,求解内参矩阵;

步骤 2利用R的单位正交性求解外参矩阵;

步骤 3求解镜头畸变参数;

步骤 4用LM(Levenberg-Marquardt)方法[36]优化标定结果,使平均重投影误差极小。

2.2 基于平行双目相机的空间点定位

假设一对双目相机满足如下关系(以下简称“理想双目系统”):

① 内参相同；② 光轴平行；③ 左右成像平面共面；④ 对极线行对齐。则可根据相似三角形原理求解空间一点到相机平面的距离,如图3所示。

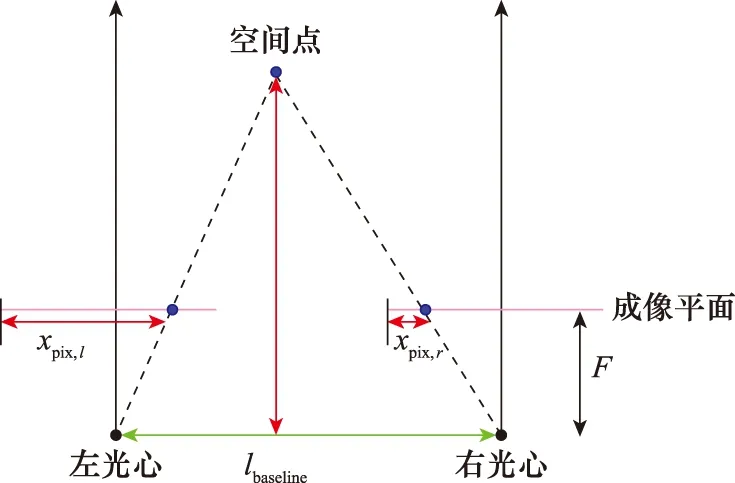
图3 平行双目相机测距Fig.3 Distance measurement with parallel cameras

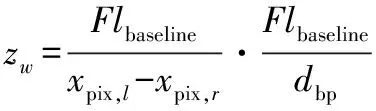
(5)

式中:lbaseline为两相机光心距离,称为基线;dbp=xpix,l-xpix,r为左右两成像平面内成像点的视差;F为焦距。

令世界系与其中一相机系重合(如左相机),则不难计算得到:

(6)

式(6)表明,当双目相机系统满足理想双目系统假设,空间点坐标可由其成像的像素坐标、相机内部参数及两相机间基线长度确定。

由于实际双目系统可能存在加工或安装误差,需进行立体校正,使其变换为理想双目系统。

首先求解两相机间的实际相对关系。空间一点P坐标(xw,yw,zw)在一组双目相机各自的相机系下坐标有如下关系:

(7)

对n张标定板进行标定,则可由n次标定获得的相机外参Rr、tr、Rl、tl求得两相机间的旋转、平移关系为

(8)

式中:Rrl、trl分别为左相机向右相机系的旋转矩阵、平移向量。

为将双目系统变换为理想系统,可进行如下操作:

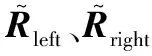
(9)

步骤 2构造Rrect=[e1,e2,e3]T使极点落于无穷远处。令e1与trl,e2与主光轴正交,e1、e2、e3正交,则有:

(10)

步骤 3构造校正矩阵:

(11)

对两相机捕获的图像分别左乘式(11),即可得到校正后的理想双目系统成像。

假设双目系统左相机光轴与受油机体轴Obxb平行,其光心在受油机机体坐标系系内位置矢量为rbc则加油锥套位置矢量可表示为

(12)

2.3 目标检测网络

在标定双目相机系统后,还需获得加油锥套中心在成像平面内的像素坐标(xpix,ypix),即可利用式(12)求得加油锥套中心在双目相机系统坐标系内的坐标。本文采用一种基于改进YOLOv4-Tiny的目标检测网络获得加油锥套中心在图像中的像素坐标。

YOLOv4系列网络在Neck部分采用了FPN(feature pyramid networks)+PAN(path aggregation network)的结构进行特征融合。其中,FPN结构能给增强high-level语义,有利于完成分类任务;PAN能增强low-level语义,有利于完成定位任务[37]。YOLOv4-Tiny是YOLOv4的轻量化版本,它牺牲了一定的精确性,但检测速度更快,更适合完成实时检测任务。

2.3.1 网络结构

YOLOv4-Tiny的网络结构如图4所示。图中,Conv表示卷积层,Leaky表示Leaky ReLU激活函数,Linear表示Linear激活函数,BN表示batch normalization层[35]。

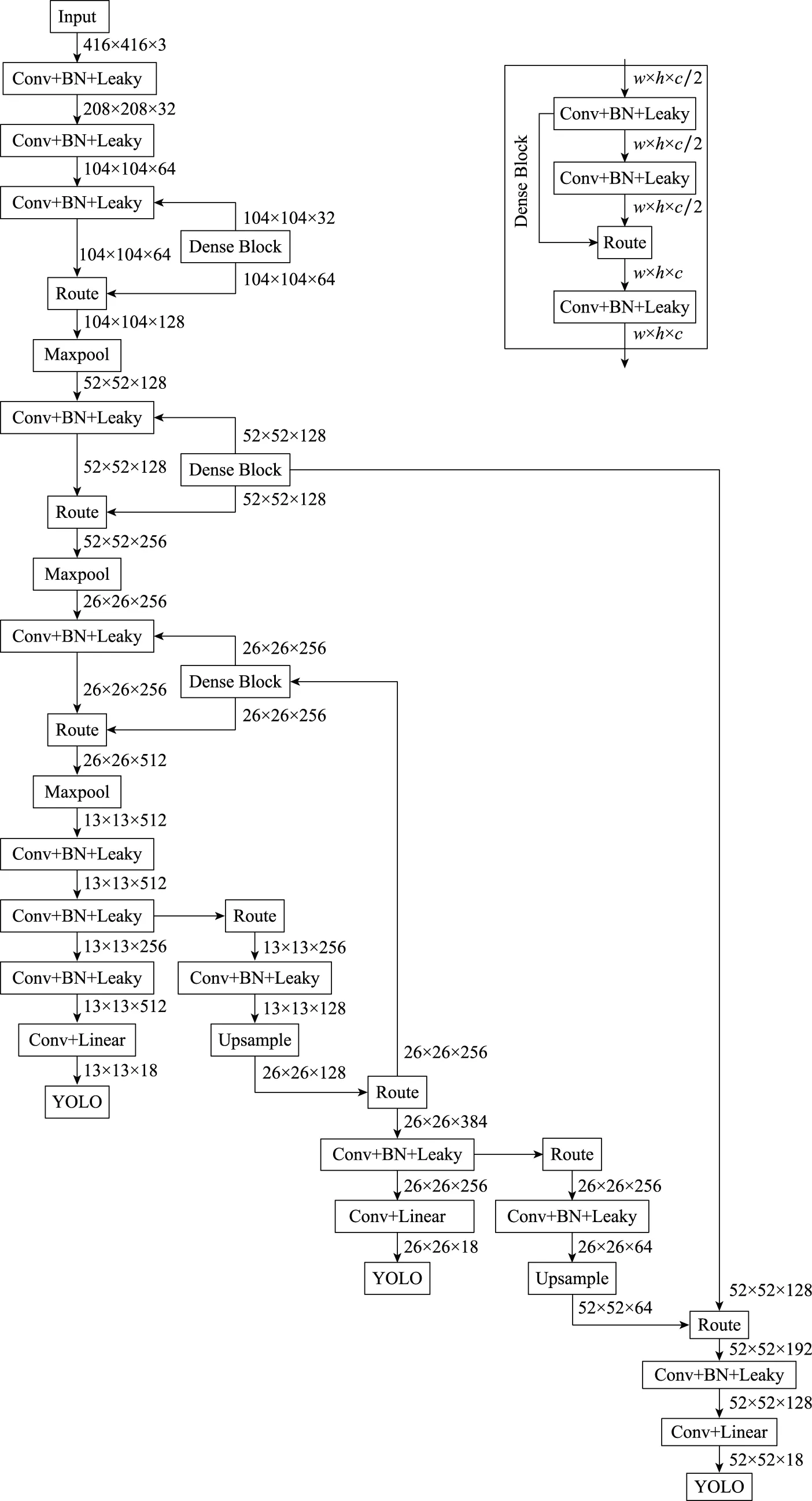
图4 YOLOv4-Tiny结构Fig.4 Structure of YOLOv4-Tiny

分析网络结构不难发现,每个YOLO层前的Conv+BN+Leaky层占用较多计算资源。以第一个YOLO层前为例,其卷积层尺度为3×3×512,输入256个特征图,需1 179 648个参数。参考network in network (NIN)方法[38],将一个3×3×512的卷积层分解为3个:1×1×128→3×3×128→1×1×512,可在实现原卷积层功能的同时,将参数减少到245 760个。对3个YOLO层前的Conv+BN+Leaky层做同样处理。

其次为增加降采样阶段的感受野,在第一个Dense Block中插入空间金字塔池化(spatial pyramid pooling, SPP)模块,如图5所示。

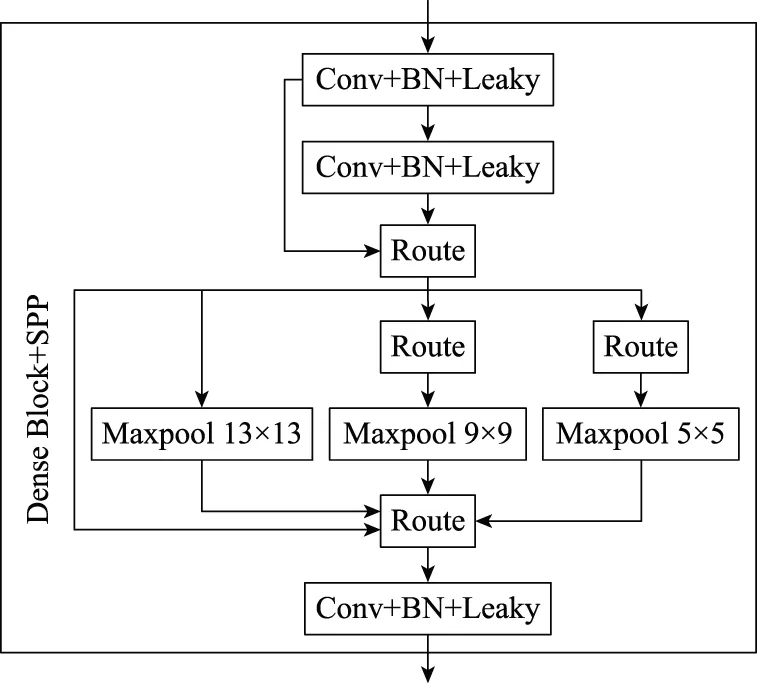
图5 在Dense Block中插入SPPFig.5 Insert SPP into Dense Block

经过如上两项修改的网络在下文中称为YOLOv4-TSPP。

2.3.2 网络输出

网络的输出为目标类别、分类置信度、目标边界框。目标边界框有4个待预测参数:(tx,ty,tw,th),如图6所示。其中,(tx,ty)为边界框中心的偏移量,(tw,th)为宽高缩放比。(bx,by,bw,bh)为预测得到的目标边界框,其中

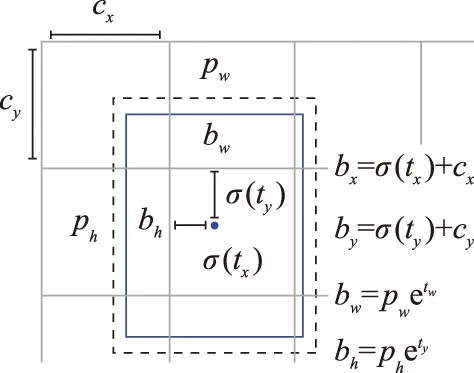
图6 边界框的预测Fig.6 Prediction of Bounding-Box

(13)

是边界框中心相对图像左上角的偏移量;

bw=pwetw,bh=phety

(14)

是边界框的宽和高;(cx,cy)是预设边界框在特征图上的中心坐标;(pw,ph)是预设边界框在特征图上的宽和高。

2.4 加油锥套椭圆拟合

近距离对接过程中,受油机需要将受油插头插入加油锥套中。前节建立的检测网络在理想状态下输出一个外接于锥套的矩形框。实际加油锥套在受油机视野中为圆形,在外接矩形所框定的范围内存在非插入目标区域,若受油机错误进入该区域则可能导致对接失败。为此,本文在获得预测矩形框的基础上建立一种“向心八点法”快速拟合锥套边界。首先作如下假设:

(1) Yolov4-TSPP已经提供了相当高交并比的外接矩形框;

(2) 加油锥套末端的稳定伞色彩沿其周向基本保持一致;

(3) 在近距离对接时,预测矩形框内大部分被锥套占据,剩余部分几乎为颜色一致的天空。

基于以上假设,建立如下椭圆边界拟合流程:

步骤 1裁剪画面,只保留矩形框内的区域;

步骤 2用Otsu方法将裁剪出的区域二值化处理[39],矩形框四个角点处应全为0或全为1;

步骤 3从矩形框的4个角点出发,各沿两条直线搜索锥套椭圆边界上的点,共寻找8个边缘点用于拟合椭圆;

步骤 4利用最小二乘法拟合出椭圆。

边缘点搜索的方法见图7,以右上角出发为例,分为图示两条路径。二值化后黑色像素为目标边缘,值为1;白色像素为背景,值为0。搜索目标为在直线路径上找到离矩形框角点最近的目标边缘点。

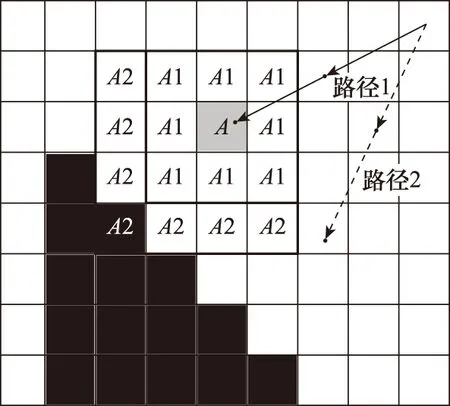
图7 边缘检测方法Fig.7 Method of edge detection

为了过滤孤立噪声点,当前点A处为1时,检查其周围3×3范围内A1的值是否全为1或大部分为1(如和为8),若是则进一步沿搜索方向取4×4范围内A2值是否全为1,或A,A1,A2的像素点集合大部分为1(如和为14)。若满足上述条件,则判断当前像素点A为边缘点。对8条路径重复上述步骤,即可得到落于锥套椭圆边界上的8个点。

相比在全局范围内进行边缘检测,“向心八点法”的计算量极小,只需在Yolov4-SPP给出的矩形框内进行8次一维搜索,即可得到加油锥套椭圆形边界。针对具体情况可对此方法进行更详细地逻辑梳理,例如:当二值图内存在一个矩形框角点与其他角点非同值,则可只取6个点进行椭圆拟合;当二值图内存在2个角点与另外2个角点非同值,可根据过去几帧预测的矩形框适当调整裁剪范围等。

2.5 加油锥套实时定位流程

结合第2.1节～第2.4节所述方法,可针对实时获取加油锥套位置及拟合其椭圆边缘这一任务目标建立一套完整的工作流程。总结为图8。

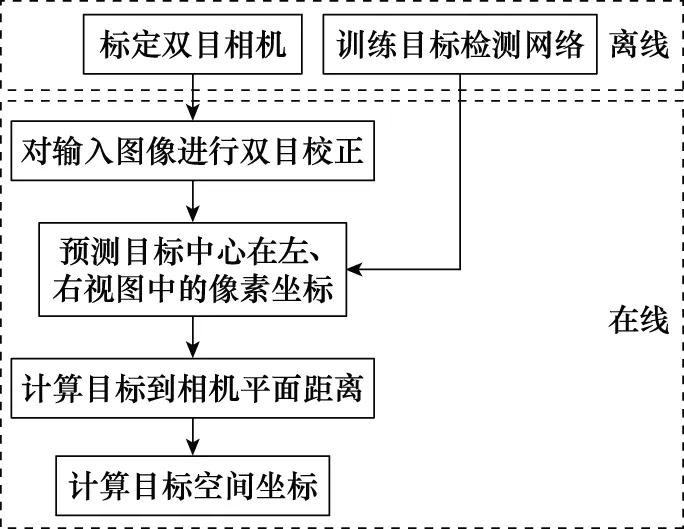
图8 锥套定位流程Fig.8 Scheme of drogue positioning

3 受油机自动对接控制律设计

前文已讨论了一种由固连于受油机上的双目相机获取加油锥套相对机体位置的方法,因此选择受油机机体坐标系进行动力学建模及控制律设计。

3.1 受油机模型

机体坐标系下受油机线性化模型定义为

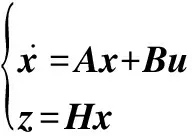
(15)

3.2 参考轨迹设计

为了避免过大的超调,引入时间t的7次多项式函数作为参考轨迹,引导受油机接近加油锥套完成对接任务,其形式为

ηr(t)=fT(t)Aco

(16)

式中:ηr=(xr,yr,zr)为位置指令;f(t)=(t4,t5,t6,t7);Aco=[ax,ay,az]为系数矩阵。参考指令可做如下设计。

对齐阶段,在时间段[0,t1]消除y,z方向的初始位置偏差(yd0,zd0):

(17)

(18)

精确跟踪阶段,在时间段[t1,t2]进行指令过渡,在时间段[t2,tf]完全跟踪锥套位置,具体地:

(19)

式中:(Δydrogue(t),Δzdrogue(t))为加油锥套相对初始位置的位移;kr(t)为过渡函数,定义为

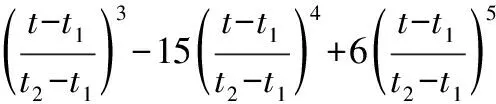
(20)

式(20)的引入可令参考轨迹指令在全任务时间内实现由7次多项式逼近向完全跟踪的平滑过渡,避免指令切换引起的震荡。

在x方向,加油锥套的运动几乎可以忽略不计,设计参考轨迹为

xr(t)=f(t)ax

(21)

由以下终端条件可求得系数向量ax为

(22)

式中:vf为对接时受油机相对加油锥套的前向速度,通常为0.5 m/s左右。

3.3 基于RSLQR増广的模型参考自适应控制

对理想系统,定义跟踪误差为

e=zd-z

(23)

为消除跟踪误差,引入积分信号:

(24)

将式(23)、式(24)代入式(15)得:

(25)

增广的系统动力学方程为

(26)

引入增广系统的状态量及系统矩阵,可将式(26)记为

(27)

基准控制量设计为增广状态的负反馈形式:

ub l=-Kxx+KceI

(28)

引入线性二次型指标:

(29)

式中:Q=diag(Q1,Q2);R为正定矩阵。引入代数Riccatti方程:

PA+ATP-PBR-1BTP+Q=0

(30)

则反馈增益为:

KLQR=[Kx,-Kc]=R-1BTP

(31)

为提供控制系统鲁棒性,可在基准控制器的基础上引入自适应控制量。考虑带有不确定性的 无人机开环系统模型为

(32)

式中:Λ表征控制系统的潜在缺陷;ΘT表征系统匹配不确定性;Φx为部分状态量。定义参考模型为

(33)

定义系统对参考模型的跟踪误差为

eref=xe-xref

(34)

总控制输入为

(35)

(36)

(37)

式中:proj(θ,y)为投影算子,其定义为

(38)

f为θ的凸函数,定义为

(39)

受油机对接控制系统的示意图如图9所示。

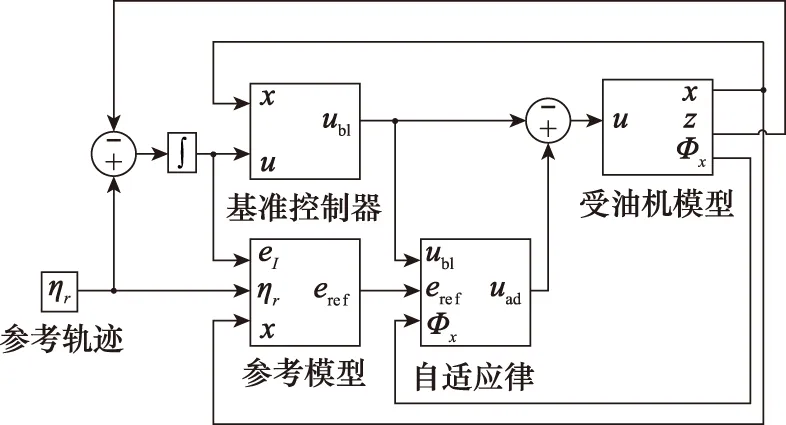
图9 对接控制系统框图Fig.9 Diagram of docking controller system

4 实验方法与结果

4.1 实验环境

双目相机系统由两台同型号相机平行架设而成;计算机为单GPU的单人电脑;标定用棋盘格采用硬质PET材质制作,棋盘格边框为6 mm,并增加背光,以提高图像对比度。具体环境如表1所示。

表1 实验环境Table 1 Experiment environment

4.2 双目视觉系统验证实验

4.2.1 双目相机标定

拍摄15组棋盘格图像,利用张正友标定法分别对两相机标定内、外参矩阵,计算重投影误差,如图10所示。图10中,对15组标定板进行重投影,其平均重投影误差为0.51 pixels,实验中输入图像大小为2 592×1 936 pixels,单张图片的最大平均重投影误差为1.17 pixels,为图片对角线长度的0.036%,可见标定结果可靠。

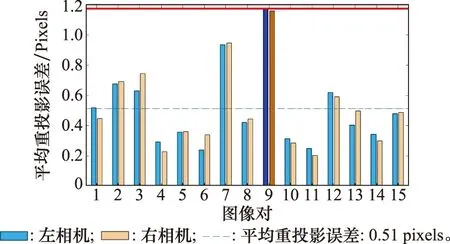
图10 重投影误差Fig.10 Reprojection error

经标定得到两相机内部参数如下。

(1) 左相机

焦距Fl=2.373 5×103

光心(cx,cy)l=(1 297,969)

径向畸变kl=[0.4 101,-1.9 595,3.2 949]T

切向畸变pl=[-0.023 5,0.001 7]T

(2) 右相机

焦距Fr=3.446 3×103

光心(cx,cy)r=(1 297,969)

径向畸变kr=[0.377 6,-1.5 757,2.8 951]T

切向畸变pr=[-0.014 3,0.008 1]T

右相机相对左相机的旋转矩阵、平移向量为

trl=[-115.416 7,-0.856 3,-0.817 0]T

以左相机光心为世界坐标系原点,两相机及所拍摄标定板在世界坐标系的位置如图11所示。

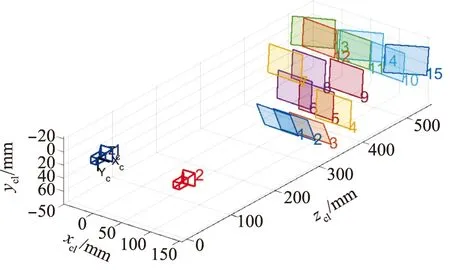
图11 相机及标定板的位置Fig.11 Location of cameras and checkboards

4.2.2 目标检测网络训练及测试

在单GPU计算机训练训检测网络,使用同样的训练参数对YOLOv4、YOLOv4-Tiny及YOLOv4-TSPP进行训练,参数设置如表2所示。

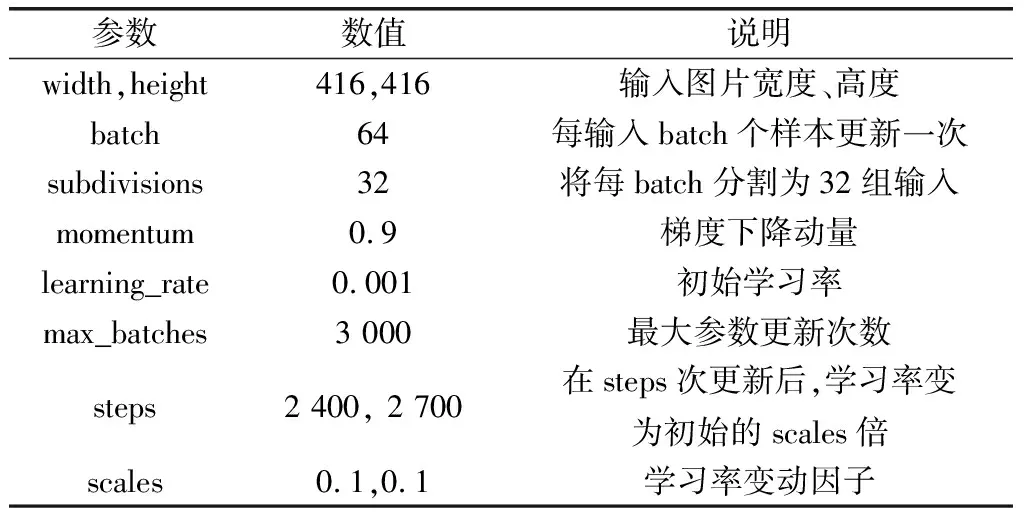
表2 训练参数Table 2 Training parameters

对数据集作如下说明。

训练集:由2 000张加油锥套缩比模型(约1∶12.5)的照片构成。为增加样本多样性并提高网络分类能力,针对加油锥套多空洞结构的特点,训练集图片具有以下特征:① 画面内存在多种不同背景,部分背景与锥套模型颜色相近;② 锥套模型存在尺寸、姿态、位置变化、部分超出画面等情况;③ 存在其他与锥套模型具有相似尺寸的圆形物体。图12是训练集部分图片示例。

图12 训练集示例Fig.12 Examples of training set

测试集:150幅由视频生成的连续图片序列,对其进行人工标注。测试集与训练集相互独立,且背景中存在干扰物。

(1) 目标检测网络性能测试

利用以上数据集按表2参数训练YOLOv4、YOLOv4-Tiny及改进的YOLOv4-TSPP,在测试集上的测试结果如表3所示。与YOLOv4-Tiny对比,YOLOv4-TSPP的卷积层浮点运算量为降低为73.51%,模型权重文件尺寸降低为69.53%;检测速度下降了9.14%,但仍然高达182 FPS,足以满足实时性要求;目标边界框预测值相对真值的平均IoU提高了5个百分点,达到88.53%,这意味着网络可以较好地预测目标所在位置及其大小。

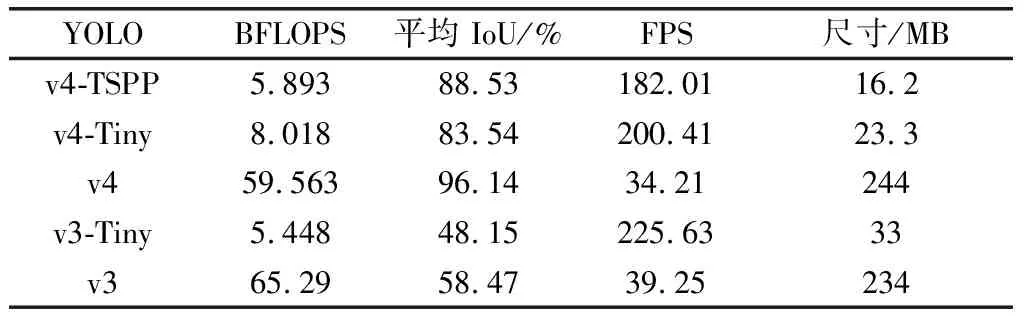
表3 检测网络在测试集上的性能对比Table 3 Performance comparison of detectors running on test set

在测试集上比了YOLOv4-TSPP与传统方法(文献[11],Camshift+卡尔曼滤波)的目标检测性能。图13显示,YOLOv4-TSPP能精确预测目标中心;使用Camshif方法时在部分时间段出现了严重的漂移,其原因在于边界框预测随着时间的推移出现扩大的情况,当聚类信息强于目标的干扰物进入预测框时,干扰物被错认为目标。

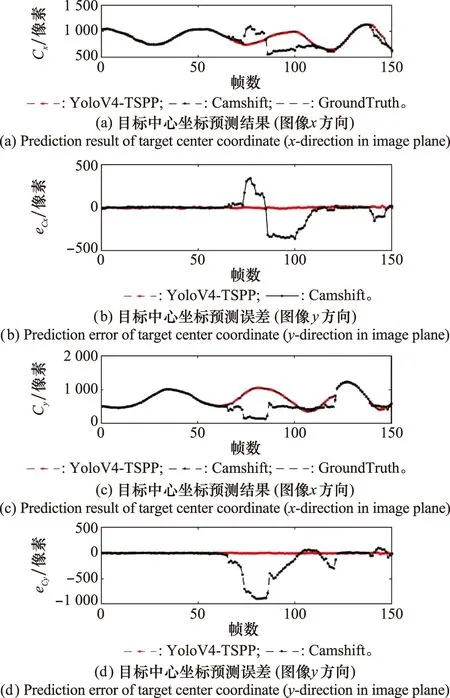
图13 图像序列预测Fig.13 Predictions on image sequence

图14统计了预测框与目标外接框真值的交并比(intersection over union, IoU),YOLOv4-TSP的预测维持了较高的IoU,而Camshift无法维持良好的预测。

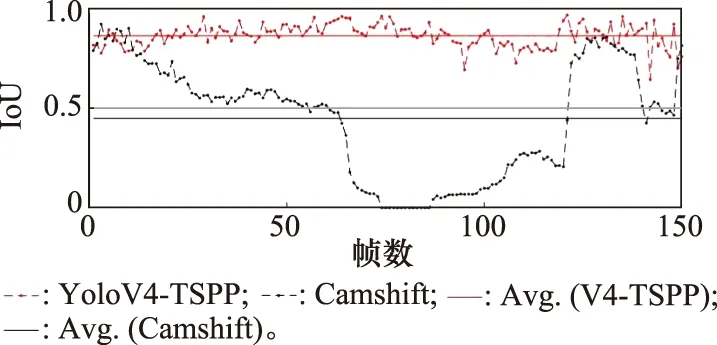
图14 图像序列IoUFig.14 IoU on image sequence

(2) 双目定位试验

用已标定双目相机拍摄若干组包含锥套模型的图像对,每组间目标沿相机光轴方向间隔50 mm,离相机的350～2 000 mm(缩比模型直径约为真实加油锥套的1/12.5,相当于验证了双目系统在距离4～25 m范围内的预测真实锥套位置的能力)。

先用YOLOv4-TSPP分别预测目标中心在左、右相机画面内的像素坐标,再利用式(6)即可求解其空间坐标。在此流程中,目标的空间定位误差主要来源于深度zw的测量误差,在相机标定足够精确的前提下,由式(6)通过zw求解xw、yw的过程不引入额外误差,因此应主要针对深度测量开展试验。

图15 双目目标检测试验(经立体校正)Fig.15 Test of binocular object detection (stereo rectified)

试验对比了对输入的双目图像进行校正及未进行校正的情况,试验结果表明:

(1) 进行双目校正有助于提升测距精度,距离预测的平均误差分别为:校正后-0.110 2 mm,未校正17.912 2 mm;定义距离的相对预测误差为绝对误差与实际距离的比值,可得每组测距的相对误差,如图16所示。

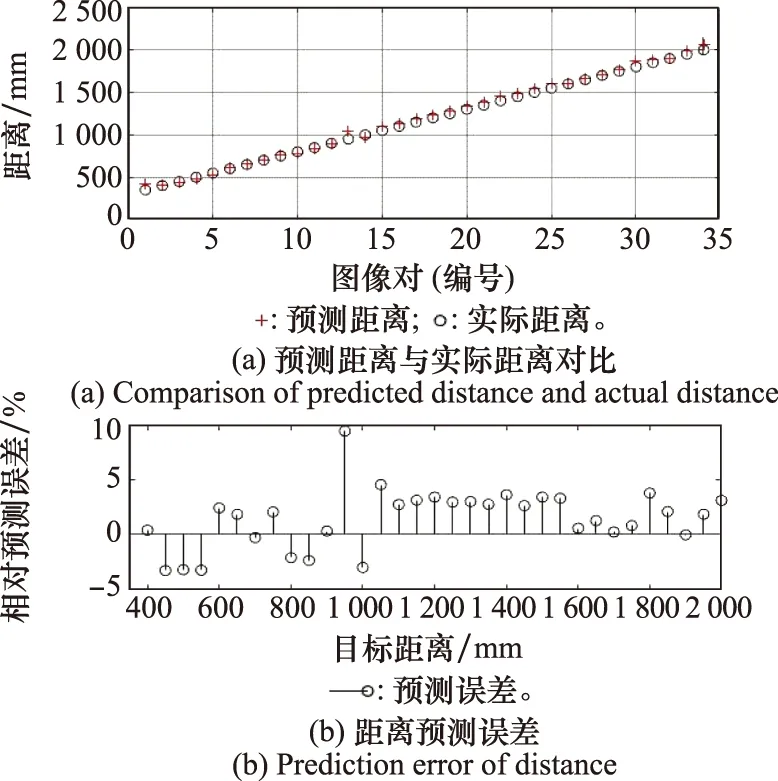
图16 距离预测结果Fig.16 Result of distance prediction

(2) 左、右两视图中目标中心的连线应落在同一水平线上。进行双目校正后,预测目标中心点对连线相对水平线的平均偏角为-0.230 7°,不进行双目校正,其平均偏角为-0.692 0°。这从侧面说明,该方法在避免进行全局水平匹配搜索的情况下,依然能够很好地预测目标中心位置。目标中心点对的连线相对水平线的偏角情况如图17所示。

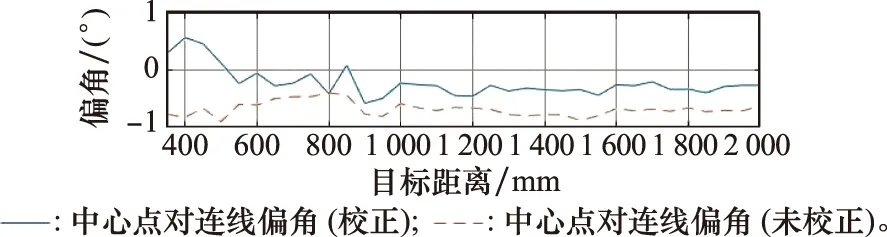
图17 预测中心连线相对水平线的偏角Fig.17 Deflection angle of connecting line between predicted centers over relative to horizontal line

图18展示了双目系统预测目标位置的结果,图中实际位置为试验过程中锥套模型摆放位置的近似空间轨迹,在深度预测具备足够精度的前提下,可以认为空间位置预测亦具备足够精度。

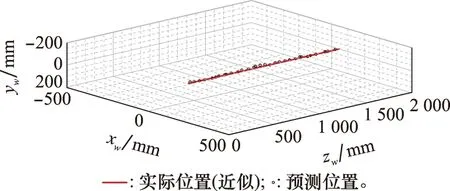
图18 目标在世界坐标系中的位置Fig.18 Location of target in world coordinates

(3) 椭圆拟合试验

对输入图像由Yolov4-TSPP在测试集上预测的矩形框后,利用第2.4节提出的向心八点法拟合得到锥套边缘。椭圆拟合的结果如图19所示,在测试集上搜索得到8个边缘点并进行椭圆拟合的平均耗时约为0.015 s(Matlab环境)。

图19 椭圆拟合效果Fig.19 Performance of ellipse fitting

4.3 对接控制系统仿真实验

第4.2节表明,基于YOLOv4-TSPP的双目系统可以有效捕捉加油锥套相对受油机的位置,因此,可基于此前提,采用文献[33]给出的状态空间模型对加油锥套运动进行仿真,并仿真验证对接控制器的性能。

以受油机作定直平飞为基准状态,飞行速度为100 m/s,飞行高度为5 000 m,进行配平并线化,加油锥套相对受油机的初始位置为(100,50,-50)。配平并线化后,式(15)中受油机状态矩阵、控制矩阵、输出矩阵分别为

--------------------

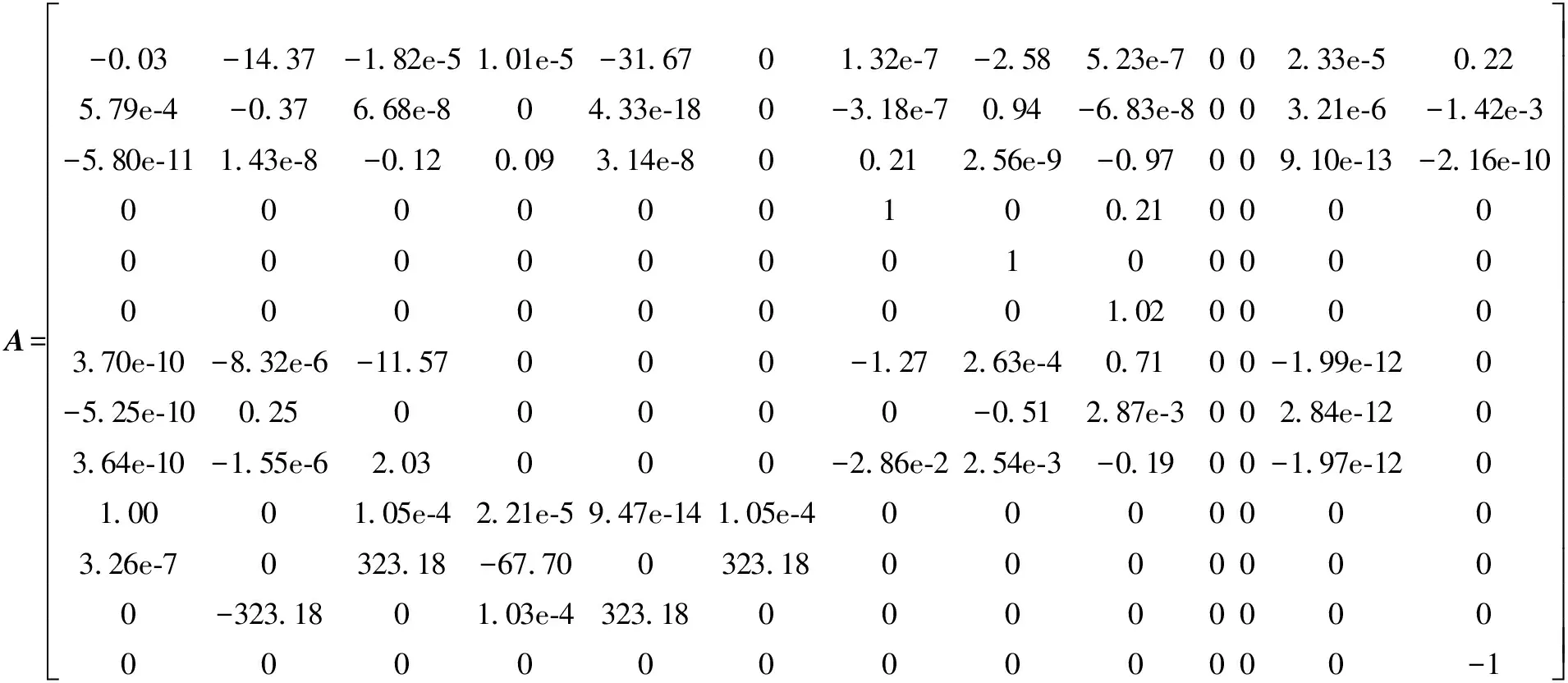
基准控制器的设计参数取为

Q=diag(20,10,10,1,10,10,1,1,1,
20,10,20,10,10,220,200,200)

R=diag(80,800,900,2 300)

其中,diag(·)表示以括号内元素为对角元素的对角阵,矩阵中除对角元素外全为0。

自适应控制器设计参数取为

ΓΘ=(0.1,0.1,1,1,1,1,1,1,1)×500
ΓU=(1,100,100,100)

仿真过程中,对受油机系统矩阵中各元素进行±30%的随机摄动,以模拟建模误差及参数不确定性。同时,在80 s时加入持续时间为10 s的Dryden紊流,在100 s、110 s、120 s依次加入x、y、z方向的突风,以检验控制器的抗风扰动性能。风扰动情况如图20所示。

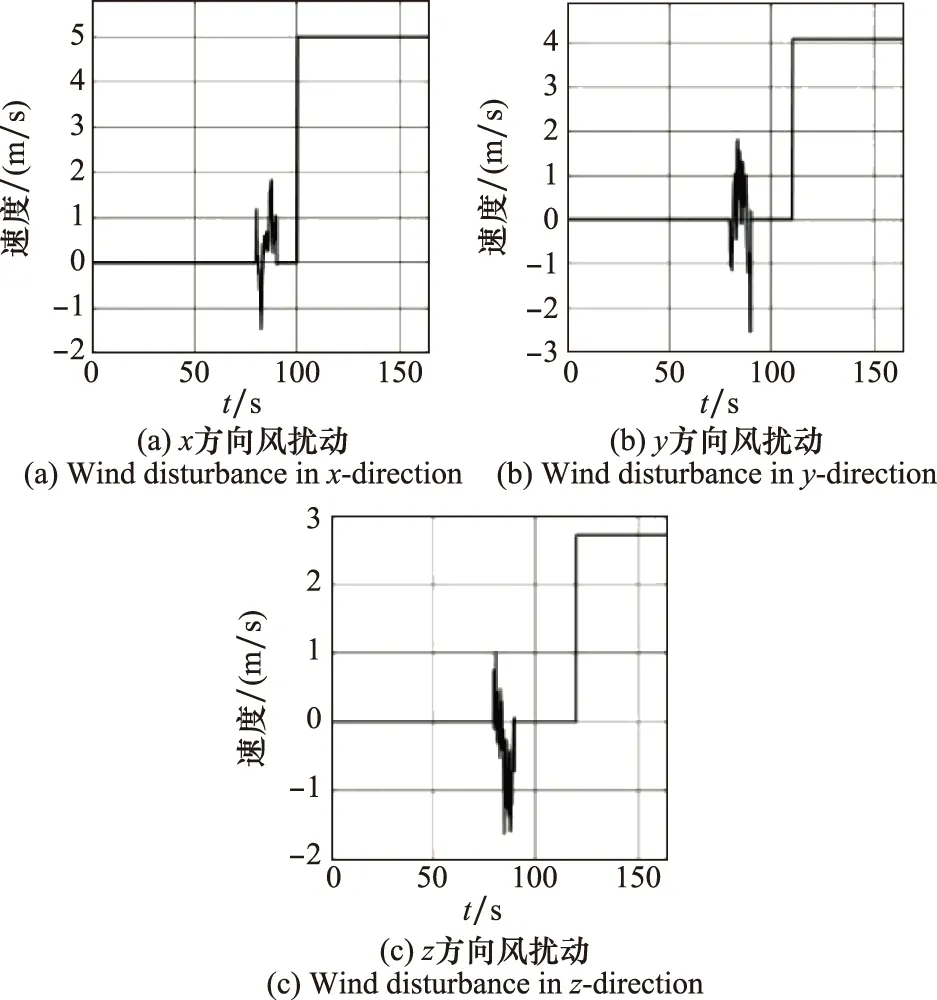
图20 风扰动Fig.20 Wind disturbances

指令跟踪的仿真结果如图21所示,结果表示为相对受油机于起始位置定直平飞时状态的增量。在无风扰动的情况下(80 s前),基于RSLQR增广的两种MRAC控制器均能使受油机跟踪参考轨迹,模型参数的摄动使自适应控制器的跟踪精度优于文献[29]提出的NZSP控制器。加入风扰动后(80 s后),NZSP方法可使受油机稳定,但受扰动后震荡幅度显著大于受投影MRAC控制的受油机;而使用传统的MRAC方法(不引入投影算子)时,在持续风扰动作用下受油机出现大幅度震荡,其原因在于式(35)中自适应量没有引入约束机制,当实际状态与参考模型状态差异较大时易引起控制量发散。

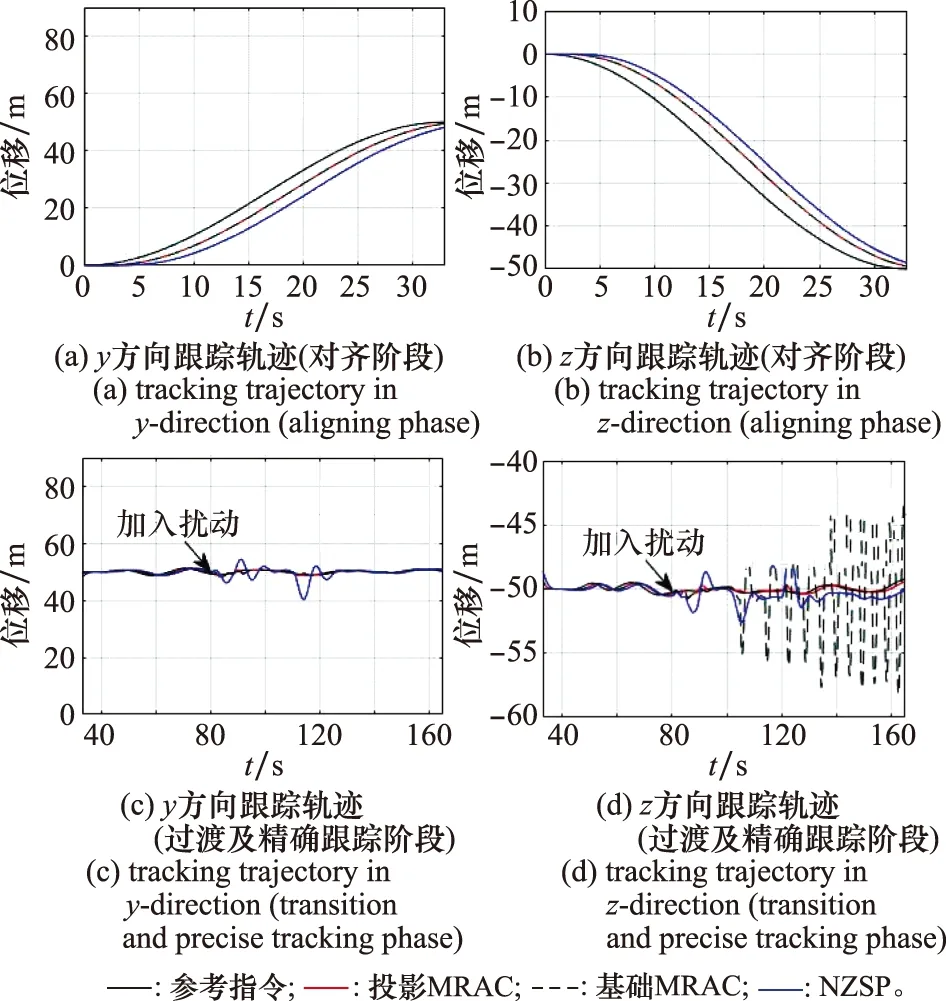
图21 y、z方向的指令跟踪Fig.21 Command tracking in y, z direction

图22显示,当存在风扰动时,各控制面的偏转角度及角速率在各自限值内(所选受油机模型舵面偏转角限值为±25°、±21.5°、±30°,偏转速率限值为±60°/s、±60°/s、±120°/s)。气流扰动带来较大的瞬时偏转速率,可通过距阵R进行调节。

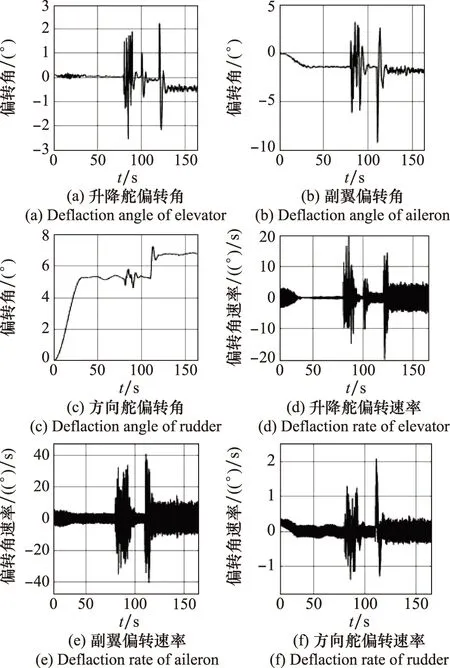
图22 控制面偏转情况Fig.22 Deflection of control surfaces

完成对齐阶段后,受油机在y-z平面内的跟踪误差如图24所示。以加油锥套的捕捉半径0.4 m为阈值,统计无风扰动的情况下精确跟踪阶段内跟踪误差小于阈值的概率为80.73%,即受油机在该阶段有80.73%的可能性对接成功,如图24(a)。存在风扰动时,如图24(b),受油机在紊流作用下跟踪误差出现一定程度的增大,在紊流停止后经过5 s左右回到较低误差水平;在突风起始时刻受油机出现较大跟踪误差,经过5 s左右回到较低误差水平,在风场稳定后跟踪误差与无风扰动时基本一致。

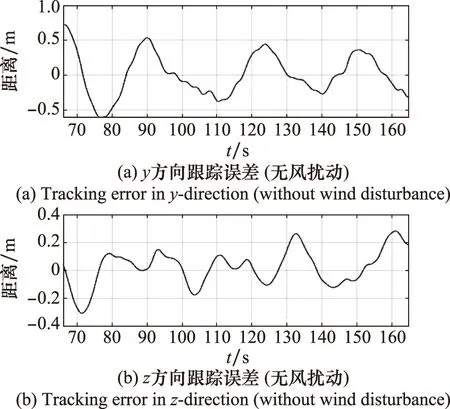
图23 y-z平面内的跟踪误差(无风扰动)Fig.23 Tracking error in y-z plane (without turbulence)

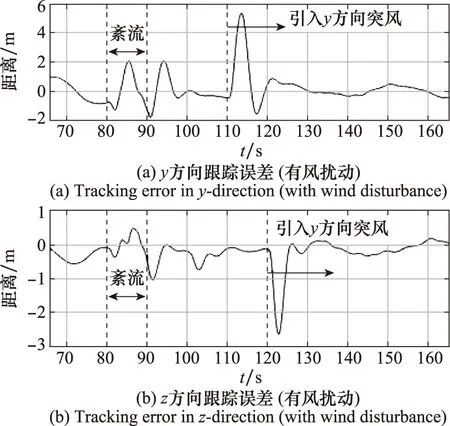
图24 y-z平面内的跟踪误差(有风扰动)Fig.24 Tracking error in y-z plane (with turbulence)

经反复试验,控制器设计参数影响如下:

(1) 增大Q阵对角线上的最后3个元素有助于抑制指令跟踪误差的产生,但同时将增大舵面偏转;增大R阵对角线上的元素有助于抑制舵面偏转,但同时将增加跟踪误差,在构造基准控制器时需权衡调整达到理想状态;

(2)增大自适应控制器设计参数ΓΘ、ΓU有助于减小图25所示的参考模型跟踪误差,即存在模型参数不确定性的飞机能更好地跟踪参考模型的状态。但该参数过大将使控制量出现较大振荡,应设计调优。

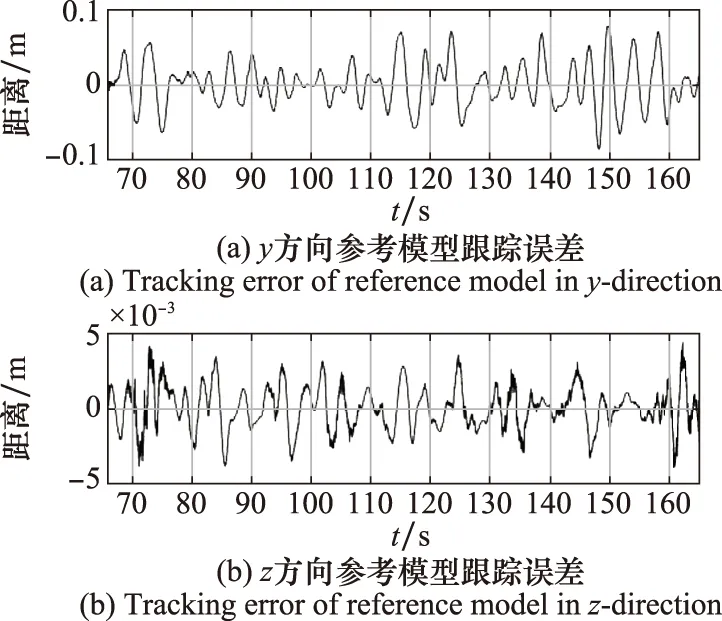
图25 参考模型跟踪误差Fig.25 Error of tracking the reference model

4 结 论

本文针对自主空中加油对接过程中锥套定位问题建立了基于双目YOLOv4-TSPP的空间定位方案,提出了一种基于YOLO目标检测结果进行向心八点搜索的锥套椭圆形边界拟合方法,并利用实体缩比模型进行了目标检测和双目测距的试验验证;针对空中加油对接控制问题提出了基于投影方法的MRAC增广控制器,进行了仿真验证。结果表明:

(1) YOLOv4-TSPP较YOLOv4-Tiny体积更小、性能更好,有较高的目标检测精度和速度,椭圆边界拟合方法满足实时性要求,符合空中加油的实际需求;

(2) 先分别从双目视野中检测目标物再进行位置匹配的方式降低了计算量,也从一定程度上摆脱了匹配算法对色彩的依赖度,可以提高双目测量方法的鲁棒性;

(3) 提出的控制方法能有效进行自主对接控制,并在机体参数存在不确定性及存在风扰动的情况下有较强的鲁棒性。