基于多尺度网格细胞的路径整合模型

赵辰豪, 吴德伟, 韩 昆, 朱浩男, 代传金

(空军工程大学信息与导航学院, 陕西 西安 710077)

0 引 言

近年来,智能导航技术成为导航技术发展的主流趋势。随着网格细胞[1]、位置细胞[2],头朝向细胞[3]、速度细胞[4]、边界细胞[5]等大脑内导航细胞的发现,产生了一种新的智能导航技术——类脑导航[6]。类脑导航作为新兴的智能导航技术,主要通过模拟大脑的空间表征机制[7],导航信息处理机制与记忆机制[8],实现自主环境探索、空间表征、路径规划、行为决策与目标导航过程[9]。区别于传统导航技术[10],类脑导航首先要建立类脑机制下的空间表征结果[11],通过类脑认知的方式对空间进行标定,具备类脑路径整合的能力。网格细胞具有六边形放电特性,被视为大脑空间定位机制的基础[12]。

目前,关于网格细胞空间定位机制的3种方案[13]为:① 多尺度网格细胞联合生成位置细胞[14];② 多尺度网格细胞的空间表征[15];③ 网格细胞放电模式的路径整合[16]。本文针对网格细胞放电模式路径整合模型的相关问题进行研究。

Islam等[17]基于头朝向细胞提出路径整合模型,该模型采用头朝向细胞感知运行体的运动方向与运行速度,采用模数计算，将互成60°角的6个头朝向细胞整合生成类似网格细胞的样式,并最终实现路径整合过程。Walters等[18]采用竞争神经网络与连续吸引子网络模拟头朝向细胞,构建基于头朝向细胞的路径整合模型。Kubie等[19]基于头朝向细胞建立了路径整合模型,通过在探索时记录访问点之间的位置,生成“捷径矩阵”,并在一定范围内完成了矢量导航任务。3种路径整合模型均采用头朝向细胞完成路径整合,未考虑网格细胞对路径整合过程的影响,对类脑机制模仿不完整。为实现完整的类脑路径整合机制,周阳等[20]采用头朝向细胞模型与网细胞模型分别感知运行体运动的方向与距离,同时引入距离细胞与头朝向细胞相关联,最终构建基于头朝向细胞与网格细胞的路径整合模型。该模型使用单一尺度的网格细胞模型,由于在曲线运动过程中单一尺度网格细胞只能感知一个位移变化量,路径整合过程结果存在较大的偶然误差。

针对以上问题,本文提出一种新型叠加整合算法构建路径整合模型,该模型由网格细胞与头朝向细胞共同构成,采用连续吸引子网络建立网格细胞模型与头朝向细胞模型,分别感知运行体的运动距离与运行方向。为提高路径整合过程的准确性,引入多尺度网格细胞模型感知多个位移变化量,采用加权平均法计算最终变化量,优化叠加算法。在运行体的不同运动情况下,灵活改变权重,使路径整合结果更加精确。

1 模 型

本文采用吸引子网络建立头朝向细胞模型与网格细胞模型,提出一种基于新型叠加算法的路径整合模型。

1.1 头朝向细胞模型

模型中的旋转细胞能整合角速度信息,调节旋转细胞与头朝向细胞的连接权重,更新头朝向细胞的放电情况。模型中头朝向细胞i的放电率[21]为

(1)

(2)

旋转细胞与头朝向细胞的连接权重为

(3)

(4)

式中:ω为头部角速度。

旋转细胞与头朝向细胞之间的连接权重与头部角速度ω有关。定义“活动包”表示头朝向细胞活性最大的细胞。根据式(4)可得,当ω>0时,将强化旋转细胞与顺时针方向的头朝向细胞连接权重,使“活动包”顺时针偏移;当ω<0时,将强化旋转细胞与逆时针方向的头朝向细胞连接权重,使“活动包”逆时针偏移。因此,头朝向细胞模型可以实时整合角速度。

1.2 网格细胞模型

本文中采用Burak等提出的单一尺度网格细胞的二维吸引子网络模型。模型中网格细胞的放电率计算方法[22]为

(5)

式中:f(x)为非线性整流函数,当x>0时,f(x)=x;当x≤0,f(x)=0;si表示神经元i的放电率;Wij为神经元i与神经元j间的连接权值;τ为时间常数;Bi为神经元i的前馈输入。

模型中设网格细胞模型为二维神经元网络,为了方便建模,规定每个神经元的优先朝向为(N,S,E,W)中的任意一个(实际中各神经元的优先朝向为连续集合[0,2π]的任意值),该优先朝向由θi决定。如图1所示,网络中相邻的4个神经元的优先朝向各不相同。神经元的优先朝向决定了神经元输出权重的移动方向与接收速度的大小。

图1 神经元的优先朝向Fig.1 Preferred direction of neurons

神经元权值矩阵内元素为

(6)

W0=a1e-γmgc|x|2-a2e-βmgc|x|2

(7)

(8)

式中：αmgc为模型速度响应系数;A(xi)为包络函数,当A(xi)=1,网格细胞网络为周期性网络。

1.3 单一尺度网格细胞路径整合模型

基于单一尺度网格细胞的路径整合模型通过记录单个网格细胞的放电次数计算运动距离,根据头朝向的变化量来判断运行体是直线运动还是曲线运动。但网格细胞的放电呈现周期性,且放电域在空间中为直线或者近似圆形区域。为了便于距离计算,算法中设置合理放电阈值Hgc,当si≥Hgc时,记网格细胞放电一次,从而使网格细胞的放电域表征空间的一个位置。如图2所示,运行体位于位置A(或位置B)时,网格细胞放电一次。

图2 网格细胞放电率曲线Fig.2 Curve of grid cell firing rate

当前时刻t所处位置A(位置B)即为网格细胞的放电野。为了避免重复计算放电次数,通过设置参数使周期性放电率曲线的上升过程首次出现si≥Hgc时,能够触发叠加算法;而同周期内再次出现si≥Hgc时,不再触发叠加算法。

为区分运行体直线运动过程与曲线运动过程,设置角度阈值与时间阈值。当运行体的头朝向变化量大于角度阈值时,认为此时进行曲线运动。单一尺度网格细胞模型的距离叠加算法如下:

Δθ=θnow-θsave;(计算头朝向变化量)

Δt=tnow-tsave;(叠加过程所用时间)

ifsi≥Hgc&& num==1

(放电率上升过程,首次大于Hgc)

num=0;

if Δθ<θth(运行体直线运动);

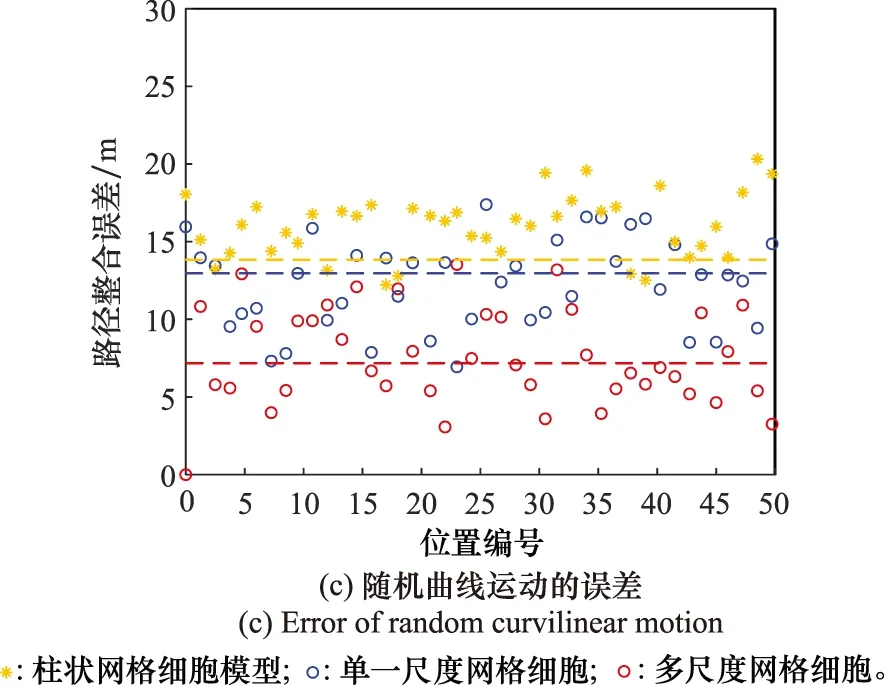
if Δt

count=count+1;

(记录网格细胞放电次数)

else

Δl=count·b;

(计算位移的变化量)

θsave=θnow,tsave=tnow;

(存储当前头朝向、时刻)

count=0,Δt=0;

(重置网格细胞放电次数、时间间隔)

end

else Δθ≥θth(运行体曲线运动);

Δl=count·b;

(计算位移的变化量)

θsave=θnow,tsave=tnow;

(存储当前头朝向、时刻)

count=0,Δt=0;

(重置网格细胞放电次数、时间间隔)

end

else

ifsi

(放电率下降过程,首次小于Hgc)

num=1;

end

end

算法中,Δθ为头朝向变化量;θsave为参考头朝向;θnow为当前头朝向;tsave为叠加过程的开始时刻;num为放电率上升沿参数;沿tnow为当前时刻;Δt为叠加过程所用时间;θth角度阈值;Tth为时间阈值;count为网格细胞放电次数;b为网格间距;Δl为位移变化量。

由算法可知,角度阈值θth能够判断运行体的运动情况,当Δθ<θth,运行体运动近似为直线运动,当Δθ≥θth时,运行体为曲线运动。当运行体进行曲线运动时,设置合理的θth,使Δθ<θth过程对应的曲线运动等效为直线运动。将曲线运动过程等效为每一小段的直线运动过程,从而完成曲线运动过程的位置计算。

1.4 多尺度网格细胞路径整合模型

根据单一尺度网格距离叠加算法可知,位移变化量Δl由网格细胞间距b与网格细胞放电次数count决定。而单一网格细胞模型仅通过单个网格细胞的放电率变化计算一次位移变化量,存在较大的偶然误差。为提高路径整合模型的精度,本节提出多尺度网格细胞路径整合模型,调整吸引子网络模型中的参数γmgc、βmgc，得到不同网格间距的网格细胞群,通过记录不同网格细胞群中不同网格细胞的放电率变化能分别感知运行体的位移变化量,对所得全部位移变化量加权取平均得到最终的位移变化量,从而减小路径整合过程的误差。

多尺度网格细胞模型中,设不同尺度网格细胞得到的位移变化量分别为:Δl1， Δl2， …， Δln;加权叠加所得位移变化量为

Δl=φ1Δl1+φ2Δl2+…+φnΔln

(9)

式中:φi为位移权重,0≤φi≤1,且满足

φ1+φ2+…+φn=1

(10)

根据不同运动情况,位移权重的取值不同。当运行体进行直线运动时,单一尺度网格细胞路径积分算法可得,不同尺度模型感知的位移变化量基本相同。在此情况下,对所得位移变化量取平均即可得到较为精确的结果。因此设置权重值:

φ1=φ2=…=φn=1/n

(11)

当运行体进行曲线运动时,由于头朝向的改变,不同尺度网格细胞的放电次数count不同。由于计数机制大尺度网格细胞模型所得位移变化量的偏差大,小尺度网格细胞模型所得位移变化量的偏差小。因此,需要增大小尺度网格细胞的权重,减小大尺度网格细胞的权重,使最终叠加结果更加精确。本文中取n=5,曲线运动时,φ1=0.5,φ2=0.3,φ3=0.2,φ4=φ5=0。

运行体在运动过程中,模型的接收输入分别为平移速度与旋转速度。根据头朝向细胞的放电情况能够判断运行体的运行方向θnow,网格细胞能够计算得到运行体相对于起始位置的运行距离Δl。因此,当运行体运动一段距离后,路径整合模型能够判断运行体沿着头朝向方向运行了一段距离,从而实现该过程的路径整合。通过路径整合模型得到运行体运动的距离与运行的方向,假设起始位置为a=[x0,y0],通过位置推算得到运行体的运动位置b=[x1,y1]。计算式为

x1=x0+Δlcosθnow

(12)

y1=y0+Δlsinθnow

(13)

将更新后的位置作为新的路径整合的起始位置,并重复上述步骤,从而实现路径整合的过程。考虑到完整记录网格细胞的重复放电以及减少计数误差,选取在该位置处放电的网格细胞为参考基准,记录该网格细胞重复放电的次数为运动过程中重复放电的次数,从而减小路径整合过程的误差。

2 仿真实验及分析

为验证路径整合模型的性能以及路径整合结果的误差,假设网格细胞模型与头朝向细胞模型感受到的速度不存在误差。仿真实验分为直线运动与曲线运动两个部分,将本文单一尺度路径整合模型与多尺度网格细胞模型的路径整合结果与文献[20]所提模型的结果进行比较,分析本文路径整合模型的性能。

2.1 仿真实验参数设置

仿真实验环境为2 500 m×2 500 m的正方形区域,直线运动过程中,运行体的运动速度为v=5 m/s,旋转速度为ω=0;曲线运动(本文的曲线运动为匀速圆周运动)过程中,运行体的运动速度为v=5 m/s,旋转速度为ω=v/r,r=1 250 m。路径整合模型能够无差别感知运行体的运动速度,通过网格细胞与头朝向细胞模型计算位移变化量与头朝向,并根据式(12)与式(13)完成路径整合过程。设置验证路径整合模型实验中的一些参数如表1所示。

表1 路径整合模型仿真参数设置Table 1 Simulation parameter setting of path integration model

2.2 仿真实验结果分析

如图3～图5所示,分别为直线过程与曲线过程的路径整合结果。对不同原理的路径整合模型的整合结果进行分析比较,验证本文方法的先进性。

图3所示为柱状网格细胞路径整合模型[20]与本文模型整合直线运动的结果。真实运动轨迹为运行体以运行速度运行的实际轨迹,准确位置为相应时刻对应的位置,其他位置为推算过程计算所得。根据图3(a)可知,柱状网格细胞路径整合模型(以下简称为柱状模型)、单一尺度网格细胞路径整合模型(以下简称为单一尺度模型)与多尺度网格细胞路径整合模型(以下简称为多尺度模型),都能够较好的完成直线运动过程的路径整合。根据图3(b)可知,通过比较3种模型的路径整合结果,柱状模型与单一尺度模型的路径整合能力相近。与二者相比,多尺度模型的路径整合结果更加接近运行体的实际位置。直线路径整合的仿真实验说明:本文所提的路径整合模型能够完成直线运动的路径整合,且与现有路径整合模型相比,多尺度网格细胞模型能够使路径整合的结果更加准确,提高路径整合精度,验证了模型在直线运动中的可行性与先进性。

图3 直线运动路径整合结果Fig.3 Results of line motion path integration

图4所示为柱状模型与本文模型整合圆周曲线运动的结果。根据图4(a)可知,柱状模型、单一尺度模型与多尺度模型都能够较好的完成曲线运动过程的路径整合。由图4(b)～图4(d)可知,在曲线运动路径整合过程中,现有柱状模型的路径整合误差较大,本文模型的路径整合误差小,且多尺度模型比单一尺度模型的路径整合结果更接近运行体的实际位置。单一尺度模型与多尺度模型的路径整合结果都存在一定的误差,但多尺度模型的误差维持在更小的水平。

图4 规则曲线运动路径整合结果Fig.4 Results of regular curves’ path integration

图5所示为柱状模型与本文模型整合随机曲线运动的结果。根据图5(a)可知,柱状模型、单一尺度模型与多尺度模型都能够较好的完成路径整合过程。由图5(b)～图5(d)可知,在路径整合的大多数位置处,路径整合的结果都存在一定的误差,但总体而言本文路径整合模型的整合结果要优于柱状模型,整合误差维持在更小的水平。

图5 不规则曲线运动路径整合结果Fig.5 Results of irregular curves’ path integration

根据图3～图5可得,本文路径整合模型能够完成直线与曲线运动的路径整合任务,但不可避免地存在整合误差。仿真结果表明,直线运动过程,柱状模型与单一尺度模型的整合误差相近,都大于多尺度模型;曲线运动过程中,本文模型路径整合能力都优于柱状模型,且与单一尺度路径整合模型相比,多尺度路径整合模型能够将路径整合的误差保持在更低的范围内。

对图3与图4的路径整合过程进行误差分析,得到某些位置的误差结果如图6所示。图6(a)为直线运动过程中某些位置路径整合的误差。由图6可知,随着运动距离的增加,柱状模型、单一尺度与多尺度网格细胞路径整合模型都存在误差,运动距离小于3 000 m时,柱状模型与单一尺度网格细胞模型的误差为12 m左右,而多尺度网格细胞模型的误差基本维持在10 m之内。因此,直线运动过程中多尺度路径整合模型的误差小于柱状模型与单一尺度路径整合模型。图6(b)为曲线运动过程中某些位置路径整合误差。由图可知,运行体在曲线运动距离约3 000 m的过程中,柱状模型的路径整合模型累计误差在15～25 m,单一尺度网格细胞路径整合模型的累计误差在10～20 m,多尺度网格细胞路径整合模型的累计误差在8～14 m。图6(c)为随机曲线运动过程中某些位置路径整合误差，由图可知，柱状模型的累计误差在10～20 m,单一尺度模型的累计误差在8～17 m,多尺度路径整合模型的累计误差在4～12 m。因此,曲线运动过程中本文所提模型(单一尺度路径整合模型与多尺度路径整合模型)的误差小于柱状路径整合模型。

图6 路径整合的误差Fig.6 Error of path integration

综上可得,本文路径整合模型能完成路径整合任务。直线运动过程中,单一尺度网格细胞路径整合模型与柱状网格细胞模型的误差相近,都大于多尺度网格细胞模型。曲线运动过程中,与柱状模型相比,本文模型(单一尺度模型与多尺度模型)的误差更小。因此,本文所提多尺度网格细胞在直线与曲线运动中路径整合的误差更小,整合结果更精确,具有可行性与先进性。

3 结 论

本文主要解决了类脑导航机制中使用多尺度网格细胞与头朝向细胞完成路径整合的问题。提出了一种基于新型叠加算法的路径整合模型,并结合多尺度网格细胞优化了叠加算法。通过仿真验证了算法的有效性,证明了多尺度路径整合模型的性能优于单一尺度模型。但实现类脑导航除了使用类脑机制完成路径整合过程外,还需要结合外部传感器优化路径整合过程,建立更加准确的类脑机制下的空间表征。因此,为实现类脑导航,需要结合视觉传感器等进行更进一步的研究。