考虑层间摩擦接触的沥青路面模量反演分析

孙广利 金 辰

(1.内蒙古公路交通投资发展有限公司 呼和浩特 010000；2.同济大学道路与交通工程教育部重点实验室 上海 201804)

采用落锤式弯沉仪(FWD)合理地反演半刚性基层沥青路面模量对路面结构承载能力评价具有重要意义。然而，目前国内外的模量反演方法大多是在弹性层状连续体系基础上建立的，没有充分考虑结构层间非连续接触条件，导致反演结果无法客观反映结构层实际情况。邱欣[1]系统分析了层间非连续接触条件对路面模量反演结果的影响，发现层间非连续接触对面层和土基的反演结果影响不大，而使基层模量反演结果显著偏低，反演值是理论值的40%～43%。查旭东[2]、杨国良[3]、朱洁[4]等分别基于同伦方法、神经网络法、迭代法等优化算法，提出了路面模量反演方法，但研究过程缺乏对实际层间接触条件的考虑。近年来，由于DBP法能够有效避免传统方法中解不唯一、初始值和局部收敛的问题，而得到了长足发展。所谓DBP法是建立弯沉盆参数(deflection basin parameters,DBP)与结构层模量的相关关系，从而利用DBP反演结构层模量。杨国良[5]、Rabbi[6]等采用DBP方法对路面结构层性能状况进行了预估评价，但研究过程忽略了层间非连续接触条件的影响，且没有充分考虑FWD荷载的动力效应。

为此，本文基于层间非连续接触条件，充分考虑FWD荷载的动力效应，建立三维动力有限元模型，构建路表弯沉盆与各结构层模量对应数据库。以数据库为基础，进行DBP敏感性分析，并利用多元回归分析方法提出结构层模量反演回归模型。

1 半刚性基层沥青路面三维动力有限元模型

1.1 路面结构及材料参数

选用我国常用的半刚性基层沥青路面结构层厚度组合，考虑到FWD冲击荷载作用持续时间较短，将各结构层视为线弹性体。根据JTG D50-2017《公路沥青路面设计规范》中推荐的路面材料模量取值范围及王旭东[7]对路面材料模量的室内试验结果，各结构层的厚度及材料参数取值见表1。

表1 常见半刚性基层沥青路面结构参数取值范围

1.2 FWD荷载与动力分析

参考国内外文献，通常采用半正弦曲线描述FWD产生的冲击荷载，见式(1)，荷载峰值pmax为0.707 MPa，荷载作用周期T为0.03 s，荷载作用半径为15 cm。

(1)

由于FWD荷载属于脉冲式荷载，荷载作用时间很短，应采用动力分析方法。同时，考虑到隐式动力分析的数值稳定性更好，且对道路结构动力响应问题更为有效[8]，故采用隐式动力分析方法来分析FWD荷载作用下的路面响应。具体分析时，还需提供用于计算阻尼矩阵的瑞利阻尼系数。本文根据国内外学者的研究成果，各结构层所选用的瑞利阻尼系数见表1。

1.3 路面层间接触条件

路面结构层之间的接触状态主要有完全黏结、部分黏结和完全光滑3种。在采用ABAQUS分析路面响应时，国内外通常采用Tie接触来模拟层间完全黏结状态；采用库仑摩擦模型来模拟层间部分黏结或完全光滑状态，并通过摩擦系数控制层间滑移行为，摩擦系数越大，层间黏结越好，摩擦系数为0时，代表层间完全光滑。

本文模型涉及2对接触面：①面层与基层接触面；②基层与土基接触面。对于面层与基层接触面，由于沥青面层与半刚性基层材料差异较大，在交通荷载和环境反复作用下，面层与基层之间的黏结作用会逐渐减弱，且大量路面调查表明，面层与基层之间层间脱开现象较多，层间黏结作用较弱。因此，采用库仑摩擦模型来模拟面层与基层之间的部分黏结状态。参考国内外学者在构建路面有限元模型时的摩擦系数取值，本文摩擦系数取为0～1[9-11]。对于基层与土基接触面，由于荷载尤其是引起水平向相对滑移的荷载随深度逐渐减小，可认为层间为连续的变形和滑移，故采用Tie接触来模拟基层与土基之间的完全黏结状态。

1.4 模型尺寸与网格划分

由于沥青路面的各结构层在水平方向无限伸展，底层在深度和水平方向无限伸展，且FWD的荷载作用区域具有对称性，故可采用1/4对称模型进行分析。经试算，最优模型长和宽取为5 m×5 m，路基深度方向取为8 m。模型底部采用固定约束，水平方向约束法向位移，对称面施加对称边界条件。模型采用C3D8R三维六面体单元进行模拟。考虑到弯沉盆测点距荷载中心的距离分别为0，20，30，45，60，90，120，150，180 cm，为方便通过节点直接获取FWD各传感器位置上的弯沉值，在靠近受荷位置的区域网格划分尺寸为5 cm。同时考虑计算精度和计算效率，在远离受荷位置的区域网格划分相对较粗。整个结构的三维动力有限元模型的示意图见图1。图中d1～d9分别代表0～180 cm位置处的9个传感器。

图1 三维动力模型示意图

1.5 有限元模型验证

邱欣利用FWD测试设备对上海沪宁高速公路进行了路表弯沉测试，获取了实测弯沉盆数据，并测试得到了结构层模量、层间摩擦系数等相关数据。相同路面结构工况下现场测试与本文数值模拟的对比结果见表2。

表2 实测弯沉数据与计算弯沉数据对比

由表2可见，两者的均方根误差RMSE在3.4%～6.2 %之间，结果相近。因此，可基于本文的建模方法，进一步开展沥青路面模量反演分析。

2 数据库构建与DBP指标敏感性分析

2.1 数据库构建

根据本文所述的建模方法与表1中的路面结构组合形式与材料参数，共对21种路面结构组合进行计算。沥青面层模量为2 000～22 000 MPa，步长取为4 000 MPa；半刚性基层模量为3 000～23 000 MPa，步长取为4 000 MPa；土基模量为100～400 MPa，步长取为100 MPa；层间摩擦系数取为0或1。故每种路面结构组合对应288种工况，本文共计算了6 048种工况，并以此构建路表弯沉盆与各结构层参数之间的对应数据库。

2.2 DBP的敏感性分析

为准确评价路面性能状态，国内外研究者提出了各种不同的DBP指标，总结概括为7类见表3。表中d1～d9分别为0～180 cm位置处的9个传感器的弯沉值，0.001 mm；r1～r9分别为9个传感器距荷载中心的距离，cm。

表3 弯沉盆参数指标

为探究面层模量Eac、基层模量Ebc、土基模量Esg对上述DBP指标的影响程度，本文以敏感度系数作为评价指标进行了敏感性分析。敏感度系数(SAF)的计算方法见式(2)，敏感度系数越大，表明两变量之间越敏感。

(2)

式中：ΔA/A为弯沉盆参数的变动比率；ΔF/F为结构层模量的变动比率。

按敏感度系数由大到小进行排序，综合分析结果见表4。

表4 弯沉盆参数敏感度系数综合排序

由表4可见，对面层模量变化较敏感的弯沉盆参数依次为：DD2>CI3>S1；对基层模量变化较敏感的弯沉盆参数依次为：CI2>S2>DD5；对土基模量变化较敏感的弯沉盆参数依次为：d9>CI8>S7，可利用敏感性较强的弯沉盆参数反演各结构层模量。

3 各结构层模量反演回归模型

基于DBP敏感性分析结果，选取对面层模量变化较敏感的DBP指标，通过多元非线性回归分析，建立了特定面层和基层厚度下，面层模量反演回归模型，见式(3)。

lnEac=aln(DD2)+bln(CI3)+clnS1+d

(3)

式中：Eac为面层模量，MPa；DD2、CI3、S1为弯沉盆参数指标；a、b、c、d为回归系数。

不同路面结构组合下，模型所对应的拟合结果见表5。

表5 面层模量回归系数取值

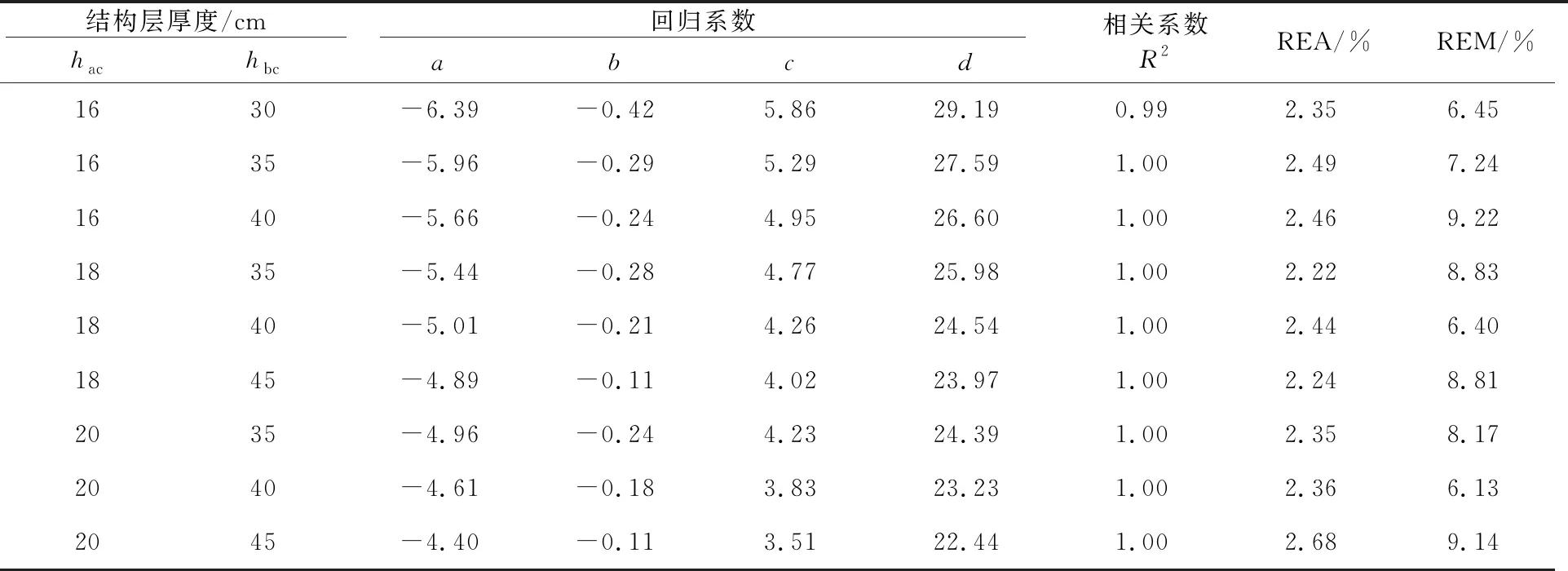
续表5

由表5可见，在较薄的面层厚度下(面层厚度小于7 cm)，面层模量的计算误差较大，REA在7.35%～8.32%之间，最大REM为32.42%；而在较厚的面层厚度下，面层模量的计算误差较小，REA在2.06%～3.17%之间，最大REM为13.53%。May等[12]在利用FWD反演结构层模量时，也发现了FWD难以准确反演薄沥青面层模量的问题，并认为这是由于薄沥青层模量对弯沉值影响较小所致，在反演分析时建议将薄沥青面层的模量设定为已知值。因此，本文不建议采用该回归模型计算薄沥青面层的模量。

随后，根据表5给出的回归系数与结构层厚度之间的对应关系，通过逐步回归分析，进一步建立了回归系数与结构层厚度的拟合方程，a、b、c、d计算方法相同，见式(4)。回归结果见表6。

a(b,c,d)=k1ln(hac,hbc)+k2hac+k3hbc+k4

(4)

式中：hac、hbc分别为面层厚度、基层厚度,cm；k1、k2、k3、k4为回归系数。

同理，建立基层模量与土基模量的反演回归模型。基层模量的回归模型见式(5)、(6)，土基模量的回归模型见式(7)、(8)。

lnEbc=alnCI2+blnS2+cln(AREA6)+d

(5)

a(b,c,d)=k1hbc+k2lnhac+k3lnhbc+k4

(6)

(7)

a(b,c)=k1ln(hac·hbc)+k2hac+k3hbc+k4

(8)

式中：Ebc、Esg分别为基层模量、土基模量，MPa；hac、hbc分别为面层厚度、基层厚度，cm；a、b、c、d、k1、k2、k3、k4为回归系数。

模型回归系数拟合结果见表6。

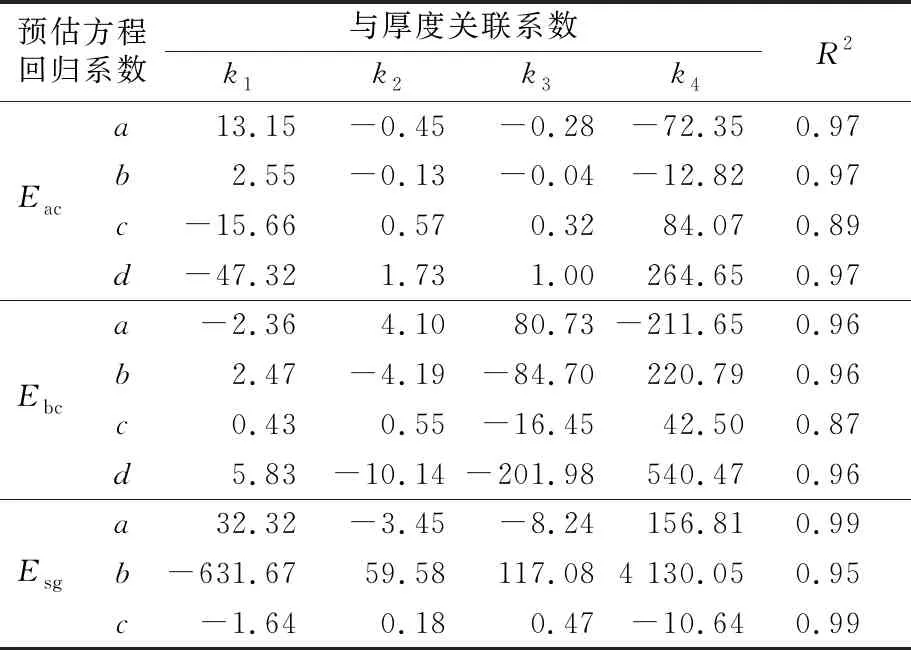
表6 面层模量回归系数与结构层厚度对应关系

经计算，基层模量的REA在1.01%～2.78%之间，最大REM为14.37%；土基模量的REA在1.39%～2.64%之间，最大REM为13.72%。由此可见，本文所得到的反演回归模型精度较高，各结构层反演模量的有效范围基本上能够满足工程分析要求。本文提出的反演回归模型适用于半刚性基层沥青路面，同时为满足反演精度要求，沥青面层适用厚度为10～20 cm，半刚性基层适用厚度为30～45 cm。

4 结论

1) 弯沉盆参数敏感性分析表明，对面层模量变化较敏感的弯沉盆参数依次为：DD2>CI3>S1；对基层模量变化较敏感的弯沉盆参数依次为：CI2>S2>DD5；对土基模量变化较敏感的弯沉盆参数依次为：d9>CI8>S7。

2) 利用多元回归分析方法，提出了考虑层间摩擦接触的结构层模量反演回归模型。该模型能够达到工程精度要求，具有形式简单，易于工程应用的优点。但对于面层厚度小于7 cm的情况，不建议采用面层模量回归模型反演面层模量。