带有扰动观测器的无人水面艇有限时间轨迹跟踪控制∗

姜朝宇 陈源宝

（1.海军驻葫芦岛代表室 葫芦岛 125004）（2.武汉第二船舶设计研究所 武汉 430205）

1 引言

无人水面艇是一种典型无人操控的非线性复杂系统。近年来，随着各学科的互融和人工智能等新技术的发展，配备新技术和新装备的无人水面艇已经广泛应用在刑侦取证、环境监测、反恐搜救等众多领域［1］。值得注意的是，由于海洋环境存在众多不确定和外界强扰动，因此无人水面艇在执行高精度轨迹跟踪控制任务时，若无有效控制策略作用，则闭环系统性能会遭受严重影响。

目前现有的无人水面艇轨迹跟踪控制策略常采用滑模控制［2～3］、反步控制［4～5］、智能控制［6］等方法。虽然上述方法均可保证闭环系统在外界扰动作用下的稳定性，但跟踪误差却无法保证在有限时间内达到满意的控制精度，这也大大限制了无人水面艇在执行一些快速机动任务的使用和需求。

基于扰动观测器DO（Disturbance Observer）的控制策略能够在很大程度上降低外界扰动对系统造成的影响。在扰动观测器设计中，一般通过构造被控对象同类结构（结构中包含模型的已知确定部分），并在此结构中引入非线性补偿函数或嵌入模糊逻辑系统/神经网络完成观测器构造，最终通过李雅普诺夫稳定性分析方法证明所设计的扰动观测器具有扰动估计能力。文献［7］提出了一种具有指数收敛速度的非线性扰动估计方法，并进一步构造了一类非线性控制器。文献［8］采用模糊逻辑系统设计了一种带有非线性扰动观测器的控制策略。文献［9］在假设扰动变化率有界的情况下，设计了一类非线性扰动观测器，并反向构造了自适应控制律以保证闭环系统的稳定性。值得注意的是，以上文献所提出的扰动观测器均存在扰动估计误差收敛速度慢的缺点，仅仅取得了渐进收敛的结果，这些方法难以快速估计外界扰动，不利于控制系统快速抑制外界扰动对系统造成的影响。

针对以上文献所提方法的不足，并结合无人水面艇自身特点和任务需求，本文将设计一种有限时间扰动观测器，并在此基础上，利用有限时间理论构造一种快速鲁棒控制方法，通过所设计的方法使得闭环系统不仅能够在较短时间内估计外界扰动并降低外界扰动对系统造成的不利影响，同时也提高了无人水面艇轨迹跟踪控制系统的鲁棒性。最后通过Simulink仿真验证方法的有效性。

2 无人水面艇模型及问题描述

选取η=[x，y，ψ]T为地球坐标系下无人水面艇系统状态向量（其中(x，y)表示船体运动位置，ψ为艏向角），通过牛顿定律可得无人水面艇非线性模型为［2～3］

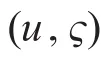
M是惯性矩阵，C(υ)是Coriolis向心力矩阵；D(υ)是阻尼矩阵，这些矩阵具体描述为

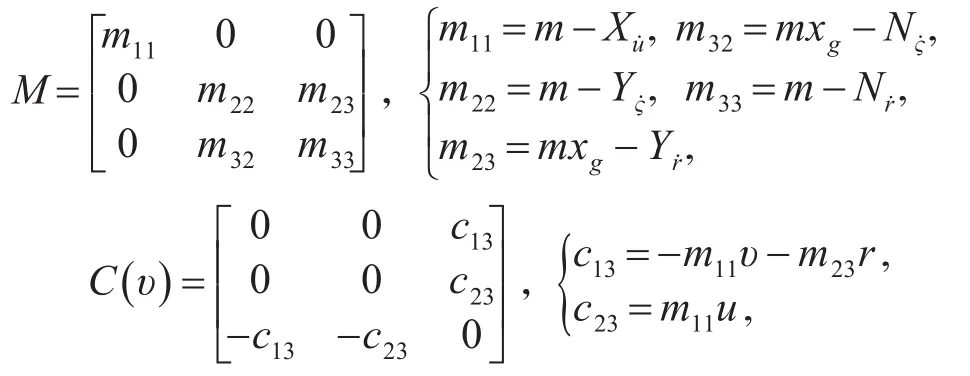
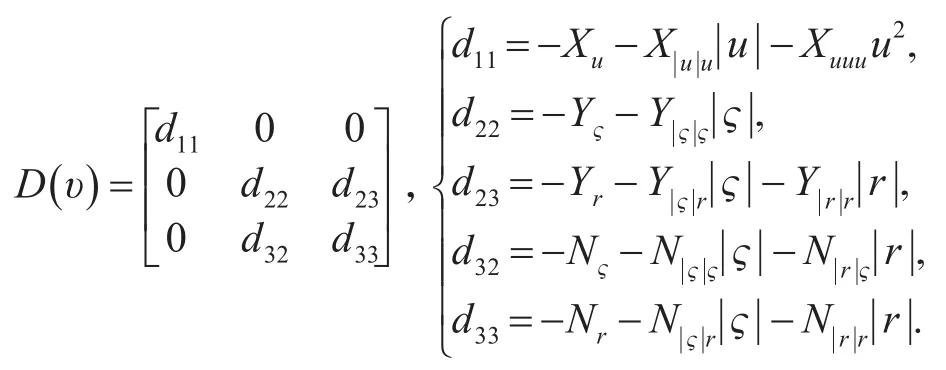
在上述参数中，m是船体质量，IZ是转动惯量，X*，Y*，和 N*是各个自由度的水动力导数［10］。除此之外，在式（1）中，τ=[τ1，τ2，τ3]T∈R3为待设计的控制输入；P=[P1，P2，P3]T∈R3为外界不确定扰动。

考虑到系统（1）中存在系统参数不确定部分，亦即M=M0+ΔM，C(υ)=C0+ΔC，D(υ)=D0+ΔD，其中M0、C0、D0是可确定的常数矩阵且满足M0＞0；ΔM 、ΔC、ΔD为不确定有界部分，因此式（1）可进一步整理为

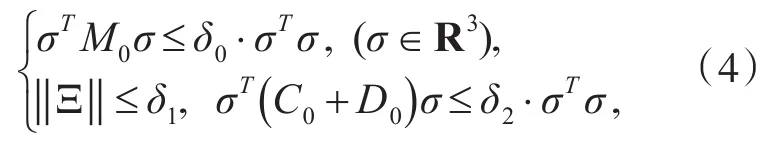
为了更好地设计控制系统，下面的假设是需要的。

假设2：无人水面艇的系统状态向量η和υ中各个物理量均可通过传感器测量得到。

本文的控制目标是：针对非线性无人水面艇系统（3），设计一种带有扰动观测器的闭环控制系统，以保证无人艇在外界扰动作用下仍然能够实现有限时间轨迹跟踪控制任务。

3 控制系统设计及稳定性分析

3.1 扰动观测器设计

首先定义一个变量为

式中，υ是系统（1）的状态，β是下面构造的辅助系统状态。

其中，η1＞δ2，η2＞δ1，η3＞0是设计参数；α1和α2是奇整数满足α2＞α1。结合式（4）和已构造的辅助系统（5），则综合扰动观测器设计为

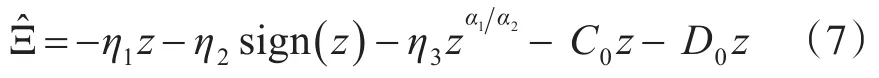
为分析和说明所设计的综合扰动观测器估计能力，下面给出严格的数学证明。选取Lyapunov能量函数为

利用式（3）～（5），对上式求导可得：

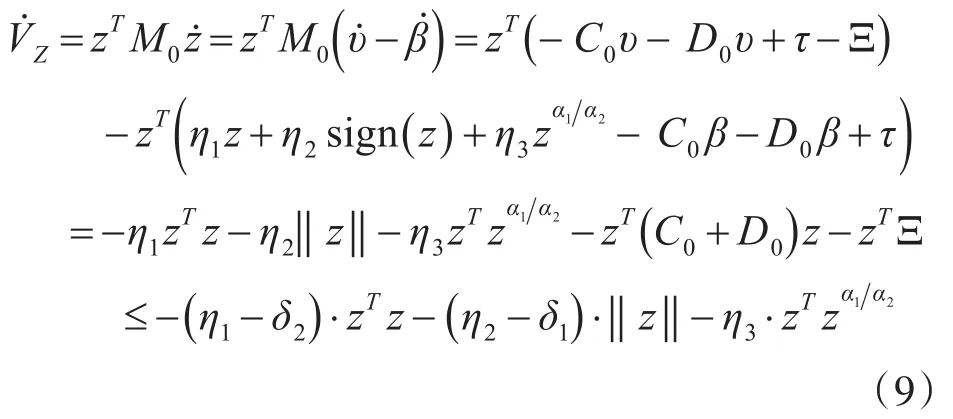
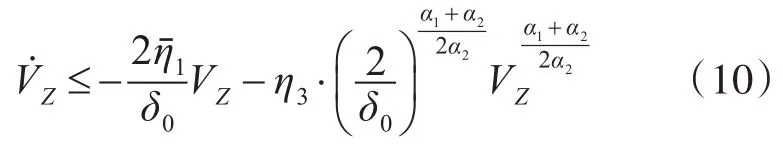
由关系式（10）可得：当 t≥tf时，VZ≡0，其中tf求解为

当t≥tf时，VZ≡0可进一步得到z≡0并且ż=0。考虑到：

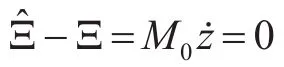
3.2 带有扰动观测器的控制律设计

本文中控制律可通过以下设计/分析步骤得到。

第一步：首先定义轨迹跟踪误差e1向量为

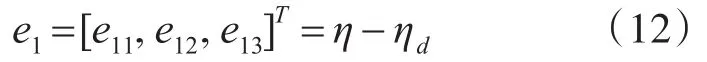
其中，ηd是期望的指令信号。对上式求导可得：

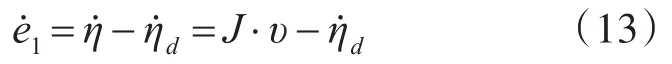
为使得闭环系统稳定，设计虚拟控制律

其中k1＞1。进一步定义速度跟踪误差向量e2并选取Lyapunov函数为

结合式（13）、（14）和（15），对式（16）求导可得到以下结果：

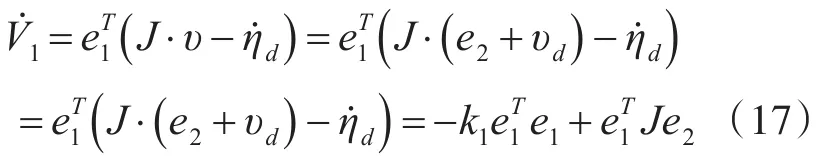
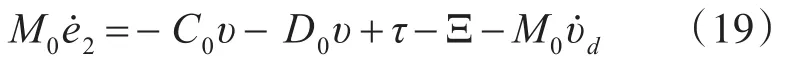
为使闭环系统具有有限时间控制能力，控制律设计如下：

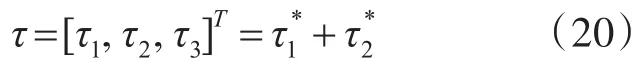
其中，0＜q＜1，k2，k3＞0。再次选取Lyapu⁃nov函数：

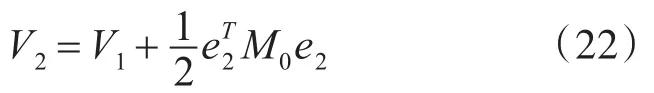
对式（22）求导并结合式（17）与式（19）得：

将控制律 τ带入上式进行整理，则有

利用Young不等式，因此有

结合不等式（25）以及 k1-0.5＞0，则式（24）可整理为

基于式（26）并利用有限时间稳定性理论［10～12］，可得到

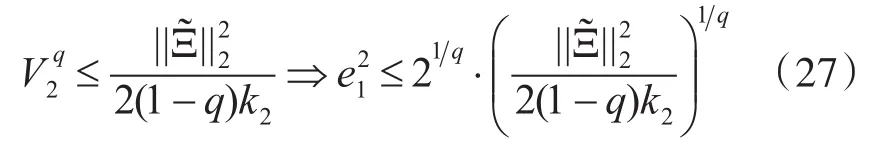
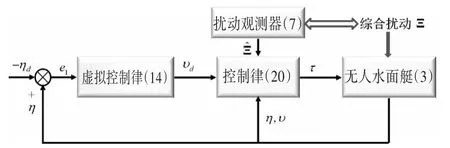
图1 闭环系统结构图

4 仿真实验与分析

为验证所设计控制方法的有效性，选取文献［13］的无人水面艇进行仿真和分析。

4.1 仿真条件和参数配置

无人艇的参数如表1所示，除此之外，系统的初始状态：η(0)=[6，3，3]，υ(0)=[1，0，0]；轨迹跟踪的指令信号为

表1 无人水面艇系统参数

外界扰动选取为

控制器参数设置为q=0.8并且k1=k2=k3=5。

4.2 仿真结果和分析

仿真结果如图2～图8所示，其中图2～4是描述无人水面艇针对给定的轨迹指令信号完成的轨迹跟踪效果。

由图2～图4可见，本文所设计的控制策略能够实现机动快速的轨迹跟踪任务，在轨迹跟踪前期，控制器根据系统反馈回的状态信息快速做出响应，因此在t≥1s后（由图5～图6可见），轨迹跟踪误差为|e11|≤0.042，|e12|≤0.037以及|e13|≤0.005。更重要的是，在整个轨迹跟踪过程中，尽管外界扰动实时作用于无人水面艇系统，但并未影响控制系统的跟踪精度和轨迹误差的快速收敛速度，这也客观说明了所设计的方法具有较强的鲁棒性。并且通过选取合适的控制参数，控制信号不存在高频抖震现象。

图2 轨迹跟踪1

图3 轨迹跟踪2

图4 轨迹跟踪3

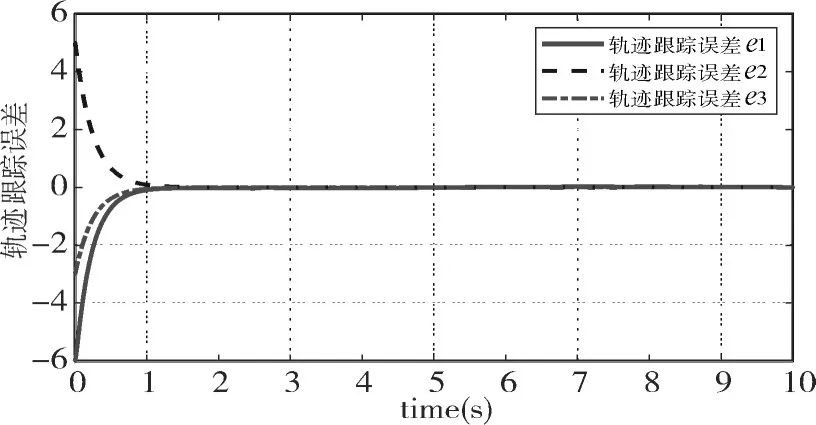
图5 轨迹跟踪误差效果

图6 二维平面轨迹跟踪

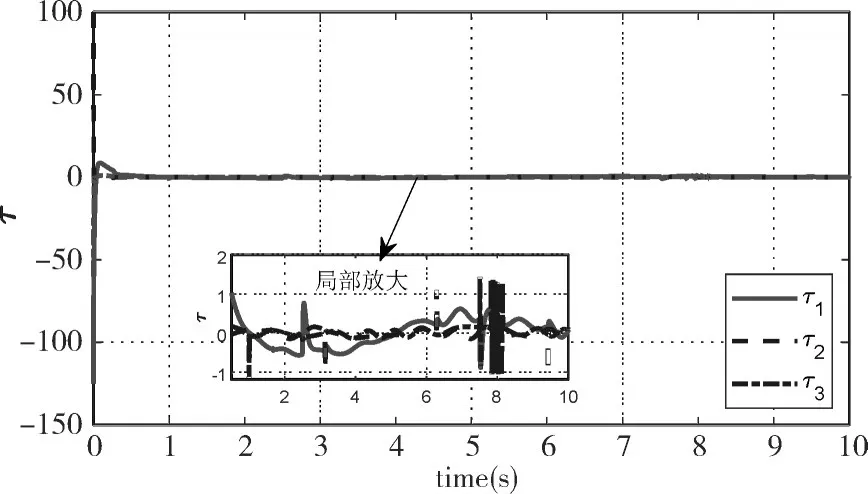
图7 控制输入信号

5 结语

本文针对外界扰动下的无人水面艇轨迹跟踪问题，设计了一种带有快速扰动观测器的鲁棒控制方法。首先针对外界扰动构建了一种新型扰动观测器，通过估计得到的扰动信息反馈给控制器，使得控制系统能够快速地消除外界扰动对系统造成的不利影响，利用Lyapunov能量函数和有限时间理论证明了所设计的控制器能够保证轨迹跟踪误差有限时间内收敛到平衡点的领域内，最后通过实验仿真验证了所设计方法的可行性和有效性。