DPSD算法在人体阻抗测量中的应用仿真

王庆祥，宁可庆，闫江

（北方工业大学信息学院，北京100144）

人体阻抗测量技术，是在人体不同部位加上特殊电极，通过电极向人体注入安全的恒定电流，检测相应部位的电压幅度和相位，从而计算出人体阻抗。在采样过程中得到的信号往往伴随着大量的噪声，同时由于人体安全电流的限制，采样得到的电压幅度在2～200 mV 之间，信噪比通常在30 dB 以下[1-7]。基于互相关原理的数字相敏检波技术，可以十分有效地从噪声中提取出与参考信号具有相关性的待测信号的幅度和相位信息，同时忽略不相关的背景噪声的干扰[8-14]。通过数字方式实现相敏检波，可以避免模拟相敏检波中由器件的不稳定所带来的噪声[15]以及器件的延迟效应所带来的相移问题。为探讨该算法的精度与采样率和采样时间的关系，文中在Matlab 中直接生成了加入高斯白噪声的正弦波电压信号。以电流注入法测量人体阻抗为例，直接对相应的电压信号用DPSD 检测，分析DPSD 对强噪声的抑制效果，从而证明DPSD 算法能够精确地提取出采样信号的幅度和相位。

1 DPSD算法的基本原理

与模拟相敏检波(Analog Phase Sensitive Detection,APSD)不同，DPSD 通过模数转换器采样后，将连续信号变成离散信号，假设两个离散电压信号频率相同且互相正交，分别为r(n)和r′(n)，采样频率为fs，每周期采样点数N=fs/f，若采样周期数为m，则有如下离散序列。

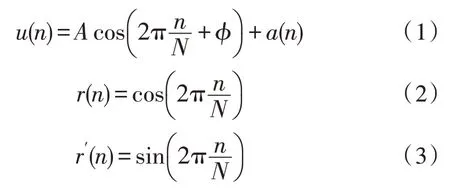
式中，n∈[0,m×N-1]。

相关函数具有降噪性，同时它还不改变原信号的特性，将离散信号u(n)分别与r(n)和r′(n)作互相关运算，得到如下估计值：

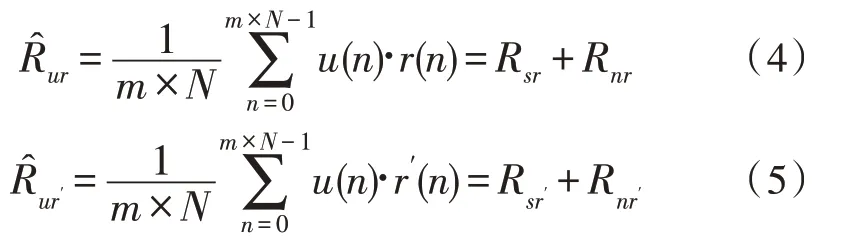
因为噪声与原信号不相关，故式中Rnr=Rnr′=0，u(n)序列分别与两正交信号相乘求和后，只保留了同相分量Rsr和正交分量Rsr′[16]：

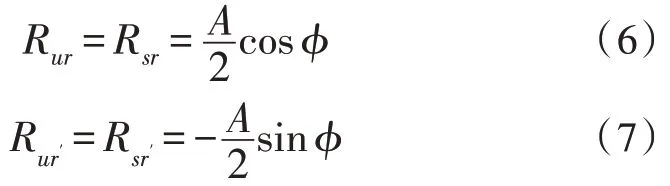
联立（6）、（7）两式，求得幅值和相角：

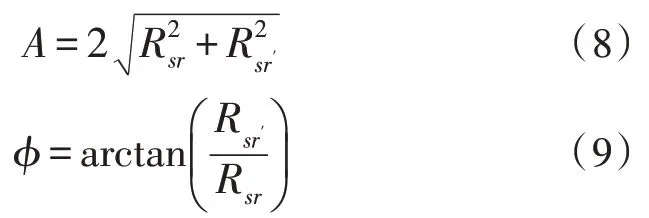
经过互相关运算，发现DPSD 算法可以去除原信号中的不相关噪声，提取出相位和幅度信息，从而达到滤波的效果。模拟滤波方法只能去除特定频率的噪声，经过模拟滤波后的波形容易产生相移，同时阻抗测量中的噪声信号通常具有随机性，故用数字滤波方法更有利于精确地计算出阻抗值。

2 基于Matlab的仿真算法实现

以电流注入法为例，当电流注入人体特定部位时，在测量电极两端产生相应的电压。故该算法以对电压信号处理为例，分析其在不同条件下的滤波效果。因高斯白噪声功率谱密度服从均匀分布，幅度分布服从高斯分布，具有代表性。所以在Matlab中生成了加入高斯噪声的电压信号序列，同时生成和其同频且相互正交的两个参考信号序列，经过互相关运算得到对应的直流分量，利用直流分量估计值，即可计算出电压信号的幅值和相角。

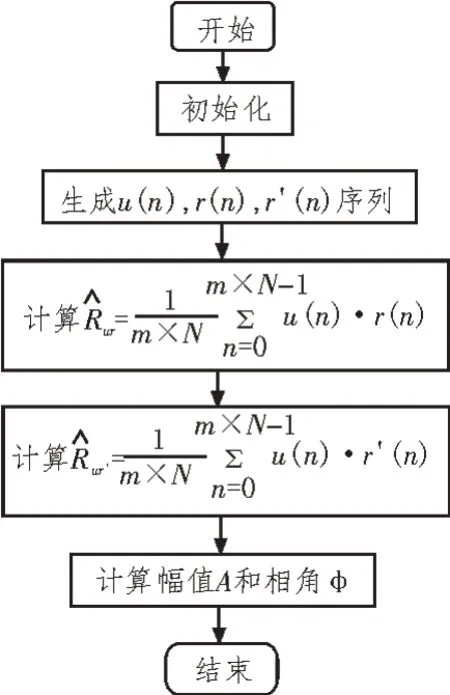
图1 电压信号检测算法流程图

DPSD算法的关键是正确设置每周期采样点数和采样周期数。设置不同频率的正弦波电压信号幅值为0.025 V，相位为10°，分别在不同的采样点数和采样周期数的条件下，对其进行30次测量并计算出其均值。

3 仿真结果

在30 dB 条件下，分别对10 kHz、100 kHz 去噪前后波形进行对比，设定原信号幅值为0.025 V，相位为10°，采样周期数m=500，总采样点数N=8 000。

3.1 10 kHz加噪和去噪信号波形及测量样点分布

1）10 kHz 加入噪声信号波形

如图2所示，在10 kHz 的正弦信号中加入高斯白噪声信号。

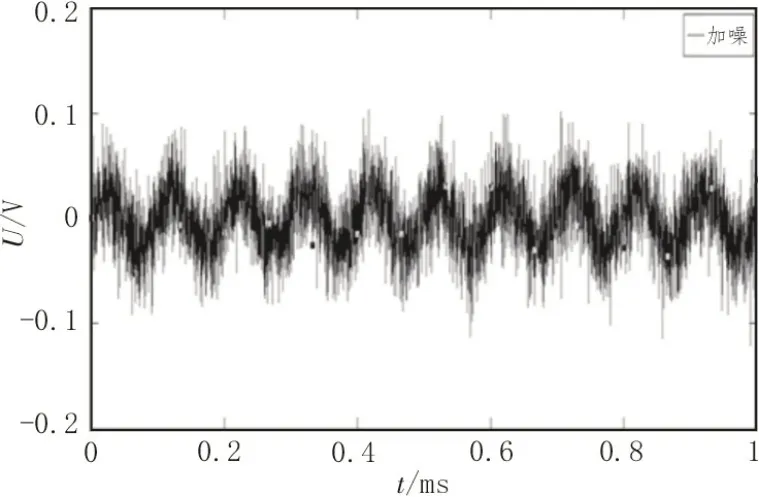
图2 10 kHz加入噪声信号波形

2）10 kHz 去除噪声信号波形

按：“叹伤”，感叹悲伤。其他文献用例如《温庭筠诗集》卷第七《经李处士杜城别业》：“忆昔几游集，今来倍叹伤。” 《秋涧先生大全文集》卷第三十五《上元仲一书记书》：“仆每读至此，未尝不废书长叹伤，岁月不我与也。”《汉语大词典》收有同义的“伤叹”，“叹伤”一词未收。

如图3所示，其为10 kHz 的正弦信号加入高斯白噪声信号在经过数控相敏检波算法去除高斯白噪声后的信号波形。

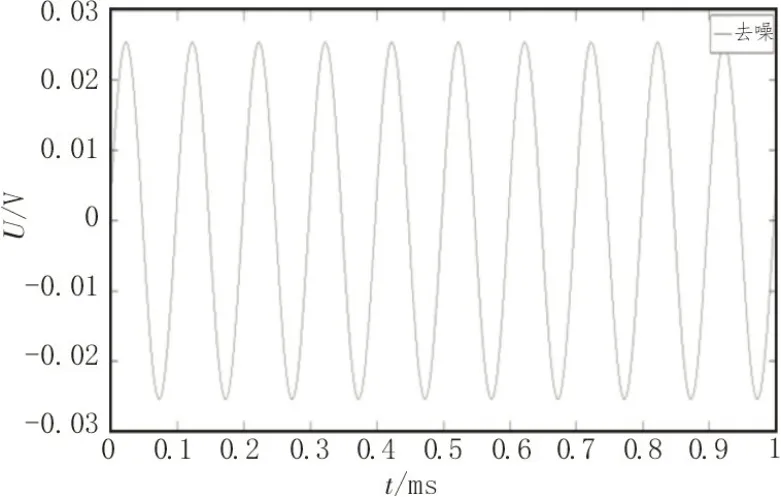
图3 10 kHz去除噪声信号波形

3）10 kHz 30 次幅值测量样点分布

如图4所示，经过去除噪声的信号波形幅值均值为0.024 985 V，误差为0.015 mV。

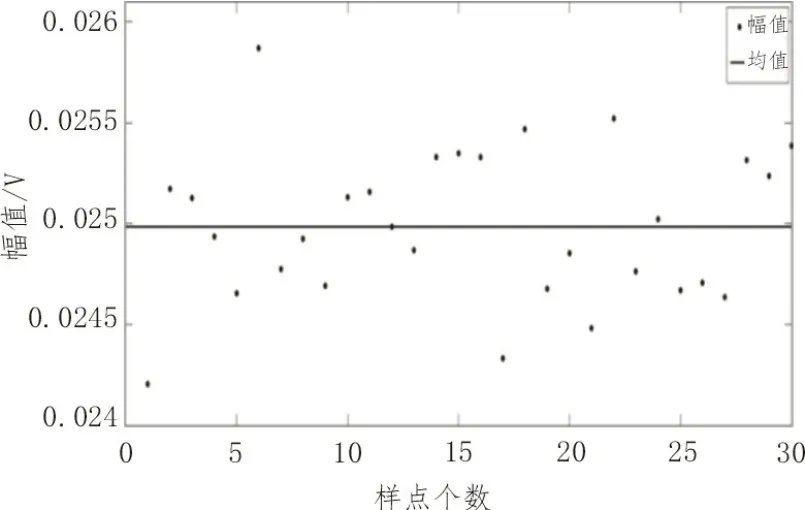
图4 10 kHz 30次样本幅值测试结果

4）10 kHz 30 次相位测量样点分布

如图5所示，经过去除噪声的信号波形相位均值为10.056 81°，误差为0.056 81°。

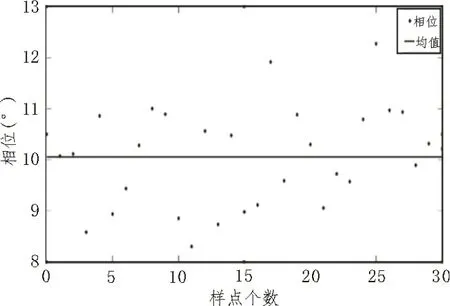
图5 10 kHz 30次样本相位测试结果

3.2 100 kHz加噪和去噪信号波形及测量样点分布

1）100 kHz 加入噪声信号波形

如图6所示，在100 kHz 的正弦信号中加入高斯白噪声信号。

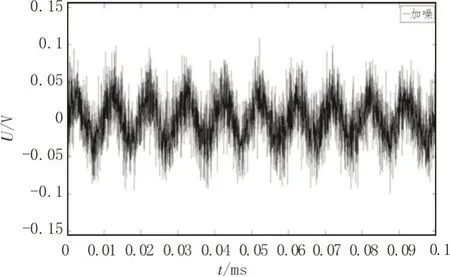
图6 100 kHz加入噪声信号波形

如图7所示，其为100 kHz 的正弦信号加入高斯白噪声信号在经过数控相敏检波算法去除高斯白噪声后的信号波形。

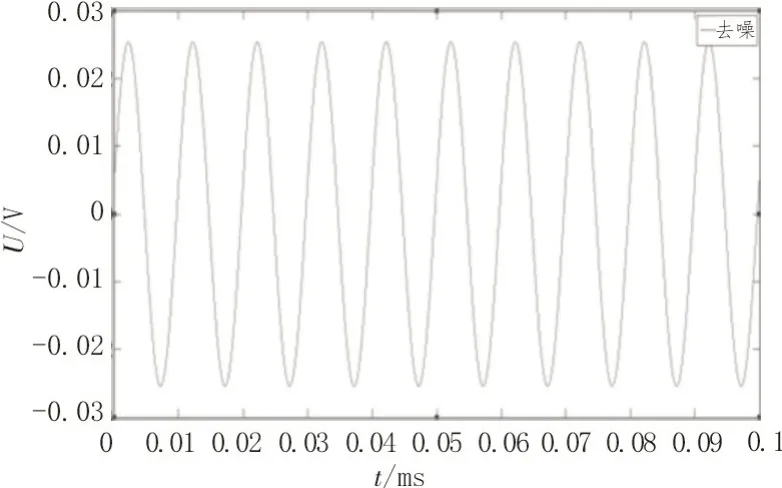
图7 100 kHz去除噪声信号波形

3）100 kHz 30 次幅值测量样点分布

如图8所示，经过去除噪声的信号波形幅值均值为0.024 993 V，误差为0.007 mV。

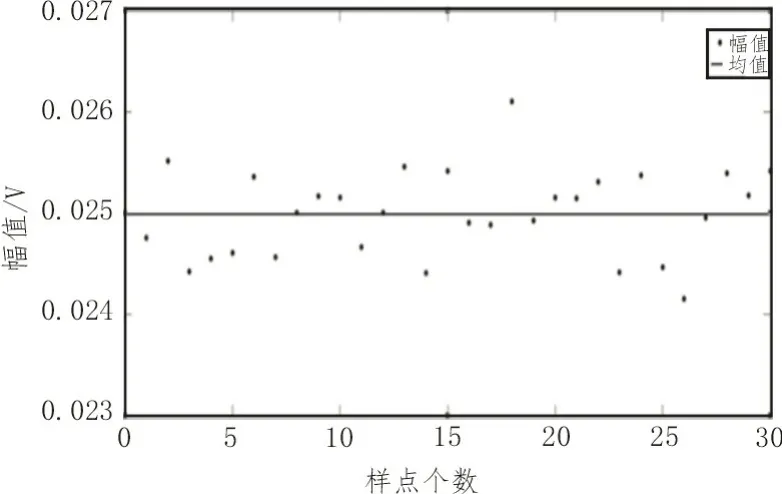
图8 100 kHz 30次样本幅值测试结果

4）100 kHz 30 次幅值测量样点分布

如图9所示，经过去除噪声的信号波形相位均值为10.016 11°，误差为0.016 11°。

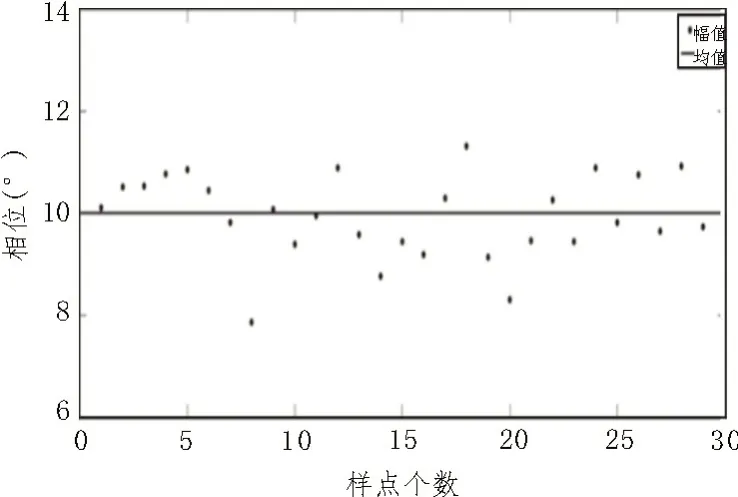
图9 100 kHz 30次样本相位测试结果

为进一步比较DPSD 算法在不同条件下的测量误差，设置信噪比为30 dB，总采样点数为8 000，每周期采样点数分别为200、500 时，得到仿真结果如表1所示。

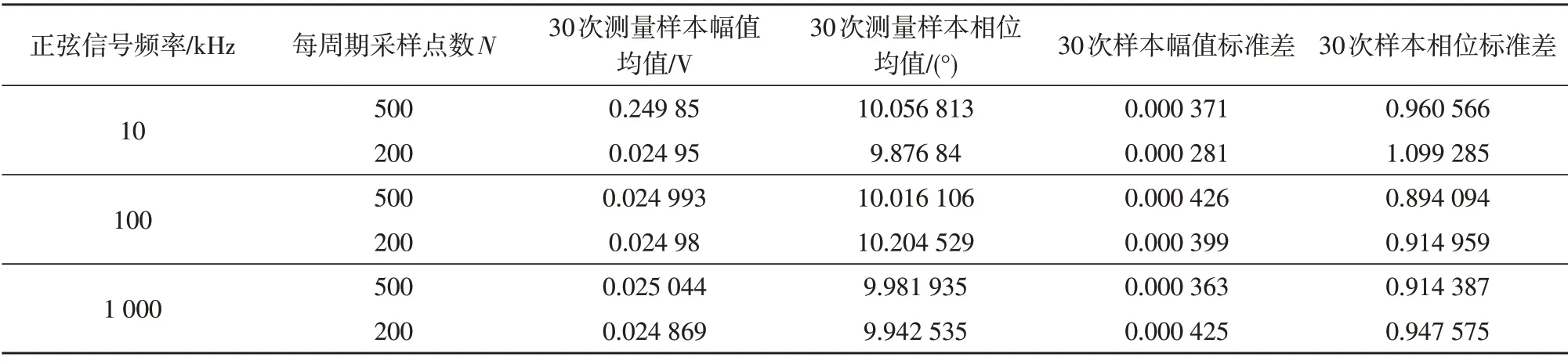
表1 不同条件下的仿真结果

4 结 论

实验证明，在不同频率下，DPSD 算法均可在误差允许的范围内计算出幅值和相角。但由于噪声的不确定性，误差也具有随机性。在不同的测试条件下幅值误差小于0.005 mV，相位误差小于0.1°。仿真分析中的噪声是人为加入的高斯白噪声，现实中的噪声往往是没有规律的，此时可通过增加采样周期数和每周期采样点数来减小测量误差。每周期采样点数和采样周期数越大，测量误差越小。因此该算法适用复杂噪声中微弱信号的检测。