LR-正则Clifford半环的性质和结构

唐宝杰 李 刚

(山东师范大学数学与统计学院,250358,济南)

1 预备知识

半环的概念由Dedekind于1894年首先提出,经过Hilbert,Huntigon,Macaulay和Noether的研究与发展,Vandiver于1934年精确定义了半环.半环是具有加法和乘法两个代数运算且满足结合律和分配律的代数系，已经被广泛运用到泛函分析、拓扑学及计算机科学等领域.近年来,对各种半群的研究已经得到了很多好的结果.本文拟利用研究半群的Clifford层次的方法,给出一个半环是LR-正则Clifford半环的充要条件及LR-正则Clifford半环的织积分解.

称半环S=(S,+,·)为幂等元半环,若∀a∈S,a+a=a·a=a.文献[1]介绍了一类非常重要的幂等元半环—带半环,这是因为在很多方面帯半环在半环中的作用如同带在半群中所起的作用.一个幂等元半环S=(S,+,·)称为带半环,若对∀a,b∈S,

a+ab+a=a,

a+ba+a=a.

一个带半环S=(S,+,·)称为T半环,若S的加法半群(S,+)是一个T带,其中T可能是“矩形”、“左(右)零”、“左(右)正则”、“正则”、“LR-正则”带等等.

引理1[2]若S是纯正群并半群,则∀a,b∈S,V+(b)+V+(a)⊆V+(a+b).

引理2[2]关于半群S下列条件等价:

1)S是一个左群；

2)S是正则的且E(S)是左零半群；

3)S≅L×G,其中L是左零半群，G是群.

引理3[3]关于半群S下列条件等价：

1)S是一个左(右)Clifford半群；

2)S是左(右)群的半格.

引理4[4]若S是加法半群为完全正则半群的半环，则

定义1[5]一个半环S称为左环，若S同构于一个左零带半环和一个环的直积.

定理1[5]一个半环S是左环的充分必要条件为

1)S的加法半群(S,+)是一个左交换群，即是一个左零带和一个交换群的直积；

2)E+(S)⊆E·(S)，其中E+(S)(E·(S))表示S的加法(乘法)半群的幂等元的集合.

定义2[5]一个半环S称为左Clifford半环，若S是左环的分配格.

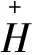
引理6[4]半群S是纯正群并半群的充分必要条件为S是矩形群的半格.

定义3[4]一个半环S称为矩形环，若S是一个矩形带半环和一个环的直积.

定理2[4]一个半环S是矩形环的充分必要条件为

1)S的加法半群(S,+)是一个矩形交换群，即是一个矩形带和一个交换群的直积；

2)E+(S)⊆E·(S)其中E+(S)(E·(S))表示S的加法(乘法)半群的幂等元的集合.

定义4[4]一个半环S称为矩形Clifford半环，若S是矩形环的分配格.

定义5[6]称带B是一个LR-正则带，如果对于任意e∈B,下列两款至少有一个成立：

1)(∀f∈B)efe=ef,

2)(∀f∈B)efe=fe.

易知，LR-正则带总是正则带，反之未必.

定义6[6]纯正群并半群S称为LR-正则 Clifford 半群，若幂等元集合E(S)是LR-正则带.

因为纯正群并半群是矩形群的半格，所以若S是LR-正则 Clifford 半群，则S是矩形群的半格且E(S)是LR-正则带.

定理3[7]半群S是拟Clifford半群的充分必要条件为S同构于织积Sl×TSr,其中Sl=[D;Lα×Tα]是左Clifford半群，Sr=[D;Tα×Rα]是右Clifford半群，且在半群同态Φ:(i,x)→x，∀(i,x)∈Sl与Ψ:(x,λ)→x，∀(x,λ)∈Sr下它们有相同的Clifford半群分量T=[D;Tα].

定理4[8]半群S是LR-C半群的充分必要条件为S同构于织积Sl×TSr其中Sl=[D;Lα×Tα]是左Clifford半群，Sr=[D;Tα×Rα]是右Clifford半群，且在半群同态Φ:(i,x)→x，∀(i,x)∈Sl与Ψ:(x,λ)→x，∀(x,λ)∈Sr下它们有相同的Clifford半群分量T=[D;Tα]；并且使得

E(S)⊆(C(E(Sl))×E(Sr))∪(E(Sl)×C(E(Sr))),

且C(E(Si))是E(Si)的中心，i=1,2.

推论1[8]半群S是LR-C半群当且仅当S同构于织积Sl×TSr，关于Clifford 半群T，Sl=[D;Lα×Tα]是左Clifford半群，Sr=[D;Tα×Rα]是右Clifford半群；且有满同态θ:Sl→T,和Φ:Sr→T，使得对∀e∈ET或者eθ-1={x},∃x∈ECSl或者eΦ-1={y},∃y∈ECSr.

2 LR-正则Clifford半环的定义与性质

定义7一个半环S称为LR-正则Clifford半环，若S是矩形环的分配格,并且E+(S)是LR-正则带.

定理5半环S是LR-正则Clifford半环的充要条件为S的加法半群(S,+)是LR-正则Clifford半群，且其极大子群是可交换的，E+(S)⊆E.(S),并且S满足以下条件:

1)∀a∈S,V+(a)+a⊇a(a+V+(a));

2)∀a,b∈S,V+(ab)+ab⊇(b+V+(b))a;

3)∀a,b∈S,V+(a)+a⊇a+ab+V+(ab)+V+(a).

a2+ax+a2=a(a+x+a)=aa=a2；

ax+a2+ax=a(x+a+x)=ax.

所以aV+(a)⊆V+(a2)，由引理4知

V+(a)+a=a2+V+(a2)⊇a2+aV+(a)=a(a+V+(a))，

∀a∈S,V+(a)+a⊇a(a+V+(a)).

同理

V+(ab)+ab=ba+V+(ba)⊇ba+V+(b)a=(b+V+(b))a，

∀a,b∈S,V+(ab)+ab⊇(b+V+(b))a.

又因为(S,+)是纯正群并半群，由引理1得∀a,b∈S,V+(b)+V+(a)⊆V+(a+b)，再由引理4得

V+(a)+a=a+ab+V+(a+ab)⊇(a+ab)+V+(ab)+V+(a)，

∀a,b∈S,V+(a)+a⊇a+ab+V+(ab)+V+(a).

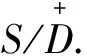
(a2+V+(a2))∩(V+(a)+a)⊇a(a+V+(a)),

(a2+V+(a2))∩(V+(a)+a)≠∅.

(ba+V+(ba)∩(V+(ba)+ab)⊇(b+V+(b))a，

(ba+V+(ba)∩(V+(ba)+ab)≠∅.

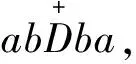
(a+ab+V+(a+ab))∩(V+(a)+a)⊇a+ab+V+(ab)+V+(a).

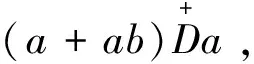
注1显然E+(S)是(S,·)上的理想.

3 LR-正则Clifford半环的织积结构

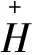
E+(S)⊆C(E+(Sl)×E+(Sr))∪(E+(Sl)×C(E+(Sr)))，

(1)

其中

且C(E+(Si))是E+(Si)的中心，i=1,2.

证充分性.由定理条件易知(S,+)=(Sl,+)×T(Sr,+)，(S,+)是拟Clifford半群，且E+(S)⊆C(E+(Sl)×E+(Sr))∪(E+(Sl)×C(E+(Sr))).

对于∀e∈E+(S),设e=((i,1Tα),(1Tα,λ))，考虑下列两种情形.

1)若e∈C(E+(Sl)×E+(Sr)),即(i,1Tα)∈C(E+(Sl))，则∀f=((j,1Tβ),(1Tβ,μ))∈E+(S),可得

e+f+e=((i,1Tα)+(j,1Tβ)+(i,1Tα),(1Tα,λ)+(1Tβ,μ)+(1Tα,λ))

=((i,1Tα)+(j,1Tβ),(1Tβ,μ)+(1Tα,λ))

=((j,1Tβ)+(i,1Tα),(1Tβ,μ)+(1Tα,λ))

=f+e

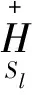
必要性. 设半环S是LR-正则Clifford半环，则易知S必是拟Clifford半环.故S同构于织积Sl×TSr，其中Sl=[D;Lα×Tα]是左Clifford半环，Sr=[D;Tα×Rα]是右Clifford半环，且在半环同态Φ:(i,x)→x,∀(i,x)∈Sl与Ψ:(x,λ)→x,∀(x,λ)∈Sr下它们有相同的Clifford半环分量T=[D;Tα].下面只需证E+(S)⊆C(E+(Sl)×E+(Sr))∪(E+(Sl)×C(E+(Sr))).

因为E+(S)是LR-正则带，对任意的e=((i,1Tα),(1Tα,λ))∈E+(S),考虑下列两种情况.

1)对任意的f∈E+(S),有e+f+e=e+f，下证(1Tα,λ)∈C(E+(Sr)).

事实上，对任意的(1Tβ,μ)∈E+(Sr)，存在(j,1Tβ)∈E+(Sl)，使得f=((j,1Tβ),(1Tβ,μ))∈E+(S).

于是

e+f+e=((i,1Tα),(1Tα,λ))+((j,1Tβ,),(1Tβ,μ))+((i,1Tα),(1Tα,λ))

=((i,1Tα)+(j,1Tβ)+(i,1Tα),(1Tα,λ)+(1Tβ,μ)+(1Tα,λ))

=((i,1Tα)+(j,1Tβ),(1Tβ,μ)+(1Tα,λ)).

e+f=((i,1Tα),(1Tα,λ))+((j,1Tβ),(1Tβ,μ))

=((i,1Tα)+(j,1Tβ),(1Tα,λ)+(1Tβ,μ))

所以

(1Tβ,μ)+(1Tα,λ)=(1Tα,λ)+(1Tβ,μ)，

即

(1Tα,λ)∈C(E+(Sr)).

2)对任意f∈E+(S)，有e+f+e=f+e，同理易证(i,1Tα)∈C(E+(Sl)).

综上可知(1)式成立，从而定理得证.