一维波方程非同位误差反馈调节
李志媛 金凤飞
(山东师范大学数学与统计学院, 250358, 济南)
1 引 言
输出调节问题,又称伺服问题,是现代控制理论中的核心问题之一.其主要任务是为给定系统设计一个反馈控制器,在保证被控系统稳定的前提下,使其某一信号跟踪上参考信号,同时抑制外在的干扰信号.现代控制理论中常见的反馈方式为状态反馈.考虑到直接获取系统状态信息的困难性,只需要测量误差信息的误差反馈在一定程度上就具有更强的现实性.由于被控系统及外系统的复杂性与不确定性,针对不同类型的系统发展了不同的处理方法.内模原理首先被应用于有限维系统[1-3],后来被推广至无穷维系统[4-8];从带有常值参考和干扰信号的分布参数系统[4],发展至带有非光滑干扰和参考信号的正则线性系统[5];由带有有界控制的输出调节问题[6,7],推广到带有无界控制的正则系统[8,9];由生成参考信号或扰动信号的外系统为有限维[10,11],引申到外系统为无穷维[12-14].Paunonen L等人[9,10]讨论了鲁棒输出调节问题是否可解,进一步对常规线性系统的鲁棒输出调节问题提出了三种动态误差反馈控制率.自适应伺服控制的主要思想是通过状态估计及参数更新来设计反馈控制律.这种思想在近年来取得了显著的研究成果[15-19],其中包括系统的扰动参数为已知[15],借助状态观测器解决带有一般外部干扰的问题[16],利用边界控制处理输出与控制同位[17]与非同位[18,19]的情形等.Smyshlyaev等人[20]系统的总结了backstepping控制方法的数学原理及主要应用.该方法通过移动全体特征值使系统达到Lyapunov意义下的稳定性,被广泛应用于解决系统的镇定问题[21,22].实现跟踪目标必须建立在系统稳定的前提下,因此backstepping方法对输出调节问题具有重要意义.Guo W等人[14]利用backstepping方法研究了带有无穷维外系统的变系数热方程的输出调节问题.
2017年,Guo W等人[18]利用误差反馈研究了带有谐波扰动的输出与控制非同位的一维波系统,并实现了量测输出趋于零的目标.本文进一步研究当系统方程中带有分布扰动时,如何利用误差反馈设计边界控制器来实现跟踪目标.考虑如下一维波方程系统:
(1)
其中,U(t)为系统(1)的控制输入,w(0,t)为调节输出,e(t)=w(0,t)-r(t)代表可测的跟踪误差,d1(t),d2(t)为一般谐波干扰信号,r(t)为给定参考信号.为了后续书写的简便,取形式为
d1(t)=asinαt+bcosαt,d2(t)=csinβt+dcosβt,r(t)=msinδt+lcosδt.
本文要利用误差信息为系统(1)设计一个边界反馈控制器,调节可测跟踪误差e(t)=w(0,t)-r(t)使其达到趋于零的目标.
全文结构安排如下:第二部分构造辅助系统的状态观测器,并证明其有效性;第三部分为原系统设计误差反馈控制律,证明闭环系统存在唯一有界解且跟踪误差渐近趋于零;第四部分给出总结.
2 状态观测器的设计
取变换
可得
(2)
且有
v(0,t)=w(0,t)-(msinδt+lcosδt)=e(t).
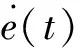
(3)
其中,k1,k2,r1,r2,r3为正参数.
令
为参数估计误差,综合系统(2)、(3)可得误差系统的具体形式为公式(4).
其中
定义系统(4)的Lyapunov函数为
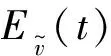
(4)
令L2(0,1)为带有由内积诱导的范数‖ · ‖ 的一般Hilbert空间,A0为L2(0,1)空间中的算子,且满足
定义状态空间V=H3(0,1)∩D(A0).
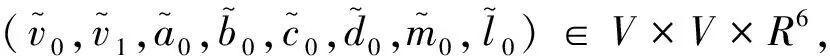
证考虑自治方程
(5)
其中F=diag(D1,D2,D3),且
函数向量(cosαt,sinαt,cosβt,sinβt,cosδt,sinδt)为系统(5)的一个解.
定义状态空间V0=H1(0,1)×L2(0,1)×R6,H=V0×R6,并且带有如下形式的内积:
定义算子A1:D(A1)(⊂H)→H,满足
(6)
将系统(4)、(5)与(6)在H中写为一个抽象形式的非线性自治发展方程
(7)
其中
由文献[14]知可建立Galerkin格式来说明系统(4)的解的存在唯一性,此处省略具体步骤.
证明完毕.
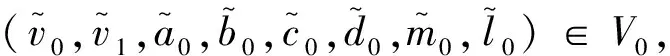
且满足
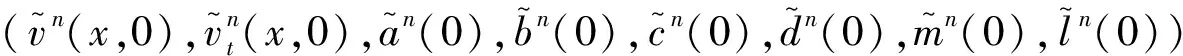
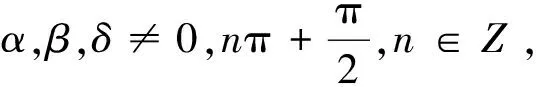
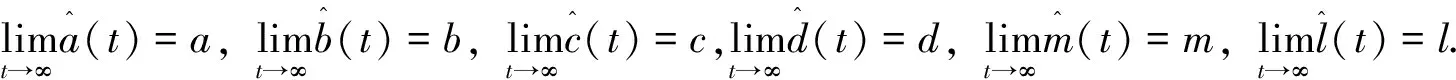
证定义函数
ξ1(t)=cosαt,η1(t)=sinαt,ξ2(t)=cosβt,η2(t)=sinβt,ξ3(t)=cosδt,η3(t)=sinδt,
构造系统(4)的Lyapunov函数
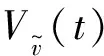
且有
Vz(t)≤Vz(0).
因此
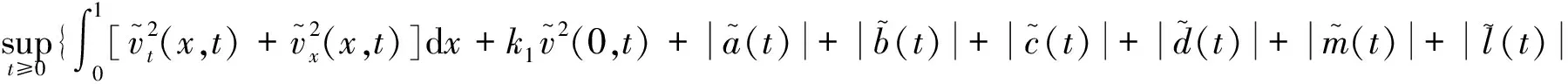
(8)
且有
定义如下函数
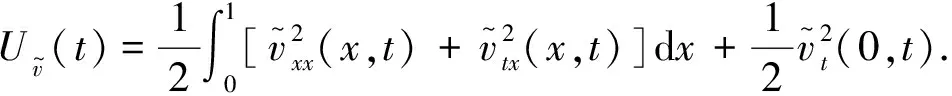
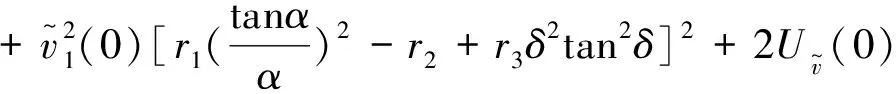
系统(7)的解轨迹为
系统(7)具有如下形式的最大不变集
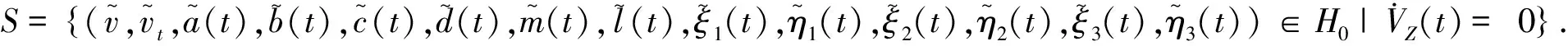
只需考虑系统
由文献[18]知,上述方程只有零解.因此系统的最大不变集S={(0,0,0,0,0,0,0,0,1,0,1,0,1,0)}.
根据Lasalle不变性原理,上述方程的零解渐近稳定.
证明完毕.
3 反馈调节器的设计
为了把干扰、参考信号和控制变换变到系统的同一端,需要构造辅助系统.
(9)
可以得到如下的辅助系统
(10)
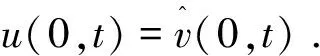
至此可为系统(10)设计一个误差反馈调节器,形式如下:
(11)
其中c0,c1为正参数.
结合控制器(11)得到下述闭环系统:
(12)
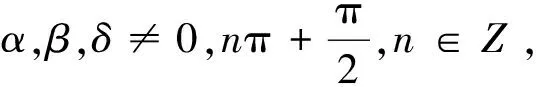
证受到文献[20]启发,引入可逆的backstepping变换
上述变换将系统(12)变为
(13)
系统(13)可被改写为
由文献[23]知,算子A2能生成稳定的C0半群,即存在常数μ,M>0,使得‖eA2t‖≤Me-μt.
由文献[24]知,算子A3对eA2t是允许的.
(u*(·,t),(·,t))T
(14)
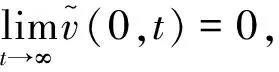
考虑到‖eA2t‖≤Me-μt,对(14)式右端第一项进行范数估计得
改写(14)式右端第二项为
其中
通过选择合适的t可以得到
由A3算子的允许性有
因此有
由backstepping变换的可逆性可以得到
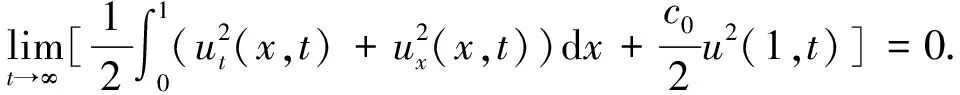
(15)
在状态空间X=H0×V0中讨论由系统(1)、(3)和(15)构成的最终闭环系统(16).
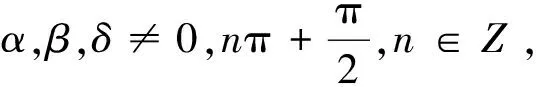
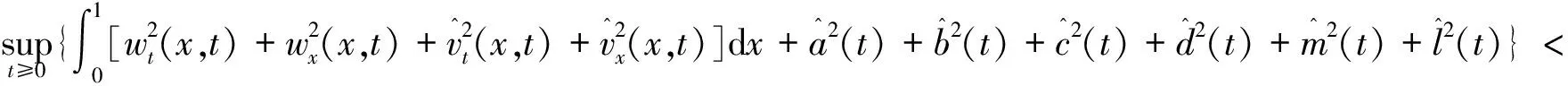
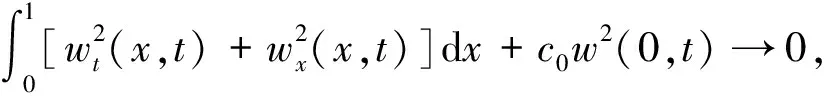
证令
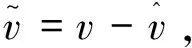
对任意初值
4 结 语
本文通过自适应控制的方法研究了受分布谐波干扰的一维波方程的输出调节问题.首先利用可测的输出来设计自适应观测器,估计扰动的未知参数并恢复系统状态.然后通过观测器和参数估计器来构造辅助系统,使得干扰与控制变成同位的情形.最后借助backstepping变换为系统设计边界误差反馈控制器,调节跟踪误差为零,并保证系统状态有界.在未来的工作中,将这种设计方法应用于不稳定或反稳定的系统将是一个值得研究的方向.

