近零介电常数材料中的非线性光学效应研究进展

宁廷银 李 鑫

(山东师范大学物理与电子科学学院，250358，济南)

1 引 言

非线性光学现象在光通讯、全光数据处理与存储[1,2]、光谱学以及量子信息技术[3,4]等方面具有非常广泛的应用[5].但通常绝大多数材料只有非常弱的非线性光学响应，一般需要很长的作用距离来实现所需的光学非线性效应，从而严重制约了器件的小型化和集成化[6].因此，在非线性光学领域一个长期以来的研究目标就是发展具有巨大光学非线性响应的材料，其光学性质能够被低功率光场显著改变.另外，优良的非线性光学材料还需要有亚皮秒的响应时间，以及与现代金属-氧化物-半导体(CMOS)制备工艺相兼容以实现纳米级尺度的集成[7].

最近研究发现，近零介电常数(Epsilon Near Zero,ENZ)材料具有非常高效的非线性光学现象[8-13]，展现出丰富的令人兴奋的性质[14-19]，与之密切相关的近零折射率(Near-Zero-index, NZI)超材料[20-23]，都引起了研究者非常大的兴趣.ENZ以及NZI相关课题的研究可以追溯到十年前的一系列理论工作，预言了此类材料中电场的巨大增强以及高效谐波产生[24-29].目前对此类材料的研究兴趣重新被激发是基于实验发现，一些重掺杂半导体，如氧化铟锡(ITO), 铝氧化锌(AZO)等，在ENZ波长处具有巨大增强的非线性响应.[9-12]比如，相关工作报道此类材料的非线性折射率比传统认为具有很大非线性系数的硒化砷玻璃还有大几个量级[30-32]，并且具有亚皮秒的超快响应.另外，最大折射率的改变也有显著增大，比如在ITO中，最大光致折射率的改变甚至可以达到0.7[11].这种空前大的折射率改变会使得此类材料在光子学有全新的应用前景[8]，特别是在光与物质相互作用长度受限的光学体系，如光学超表面[33].除了光致折射率改变，其他ENZ材料增强的非线性光学效应，如谐波产生[9,10,34]，光波混频与频率转变[12,35]以及电光效应[36-38]等被广泛报道.基于EZN材料的高效实用的光学器件，如全光与电光调制器被提出.表I给出了几种EZN材料的三阶非线性系数.

本文主要概述EZN材料和NZI材料的光学性质和实际应用.首先从理论上理解ENZ材料巨大非线性响应的机理，然后综述近年来ENZ行为与光学非线性响应相关联的实验研究工作，最后是对该新生领域的总结与展望.

2 ENZ材料及其非线性光学增强的机理讨论

ENZ材料在某一特定波长处其介电常数的实部接近为零，此波长记为ZE.类似地，NZI材料在某一特定波长处其折射率(或等效折射率)的实部接近为零，此波长记为ZI.我们知道材料的折射率表示为其中ε为相对介电常数，μ为相对磁导率.材料的介电常数和磁导率的实部均趋于零时，折射率n的实部趋于零，因此，NZI材料也被称为介电和磁导率近零(Epsilon and Mu Near Zero, EMNZ)或双零材料.[21,42]对一般非磁性介质来讲，μ1，其折射率其中上标一撇和两撇分别代表实部和虚部.在近零介电常数波长ZE处ε′=0，此时，比如对于ITO来讲，其介电常数实部为0时，其虚部ε″0.3，此时n′=0.4[11,43].因此，ENZ和NZI还以有一定区别的.

下面我们对ENZ材料体系做一下简要概述.主要分为自然界中存在的ENZ材料和人工超构材料两种类型.

2.1EZN材料体系

2.1.1 自然存在的材料体系 自然存在的EZN材料体系主要有金属、半金属、掺杂半导体、声子材料及带间材料等几大类.

其次，半金属材料由金属元素与介质元素化合得到，其载流子浓度(1～51022cm-3)比金属有显著下降.通常其介电常数在可见光波段存在零值.最近EZN半金属材料研究主要集中在硅化物[50-52]、过渡族金属氮化物[53-58]、锗化物[59，60]等.其中，过渡族金属氮化物因其ENZ在可见光波段的纳米光子学应用而被广泛研究.[55,61-63]代表性的过渡族金属氮化物半金属材料，比如，TiN(ZE=500 nm,ε″=3), ZrN(ZE=430 nm,ε″=1.1),HfN(ZE=430 nm,ε″=1.3)，具有在蓝绿光区域的ENZ效应.其他过渡族金属氮化物半金属材料，如VN，YN，WN等，也被预言具有和前述氮化物相似的性质[64].相对于金属，半金属材料除了ENZ在可见与近红外波段的优势外，还有一个重要优势就是ZE可以通过调控半金属材料的组分及结构实现很宽范围内的可调特性，以及可以通过外加电场或光场激发实现动态可调.这种可调特性可以实现基于此类材料的特殊光子学器件应用领域.

再次，掺杂半导体，特别是掺杂的氧化物[43,54,65-67]、氮化物[68]以及砷化物[69,70]是最通用和研究最广泛的ENZ和NZI材料.掺杂半导体具有几个优异的性质：宽的NZI和ENZ可调性；满足NZI和ENZ时低的损耗；Drude响应导致的宽的NZI和EZN带宽；NZI和/或ENZ波长的静态和动态可调性.典型地，高掺杂的氧化物材料，比如In:SnO, Ga:ZnO, In:CdO等ZE可以达到1 150 nm[34]，而Si:InAs甚至可以达到远红外15 800 nm[70].通过改变基本材料、组分和掺杂程度，可以实现从近红外到远红外整个光谱范围内的可调.轻掺杂半导体，比如ZnO[71]，InAs[70]，Si77等可以在中红外波段实现ENZ[72].此波段的ENZ和NZI效应将带来一些新的应用，比如，热成像，化学传感及化学振动谱等.另外，由于轻掺杂减小的载流子浓度，通常来讲其Drude损耗要比重掺杂半导体小.另外，掺杂半导体材料覆盖很宽的材料体系，可以用成熟的方法和技术制备，比如溅射法[53]，激光烧蚀法[73]，化学气相沉积法[74]，分子束外延[65]，及液相化学法[66]等.总之，由于掺杂半导体的优异可调性、低光学损耗以及成熟完善的制备方法，使得此类材料体系在近红外波段的NZI和ENZ研究方兴未艾.

声子材料表现出振动共振性而具有金属性波长区域[75,76].一般来讲，这种情况发生在横光学声子模和纵光学声子模之间，此区域也被称为剩余射线带[72,77].此类效应可以用洛伦茨公式说明[76]，如图1所示.由图可以直观地看出在近红外光谱范围具有NZI和EZN效应.此类效应自然的存在于异质半导体(如，AlN[78]，GaN[79]和SiC[75]等)，以及一些二维材料体系，如六角氮化硼(hBN)[80-82]声子材料也具有一个非常重要的特点，即在零波长处具有比较低的损耗，比如SiC(ZE=10 500 nm，ε″=0.3)[83],InP(ZE=6 500 nm，ε″=0.1)[84], hBN(ZE=12 350 nm，ε″=0.05)[82].诚然，低的损耗对很多光学应用来讲是非常关键的，比如高品质因子的声子共振应用于光开关[77]，但由于这种共振是由于材料中的声子振动模式，使得NZI或EZN效应的波长位置很难实现静态可调，但使用某些方法可以实现动态调控[85].声子材料是目前最接近零折射的材料，因此为研究基础物理现象及光与物质相互提供了基础平台.

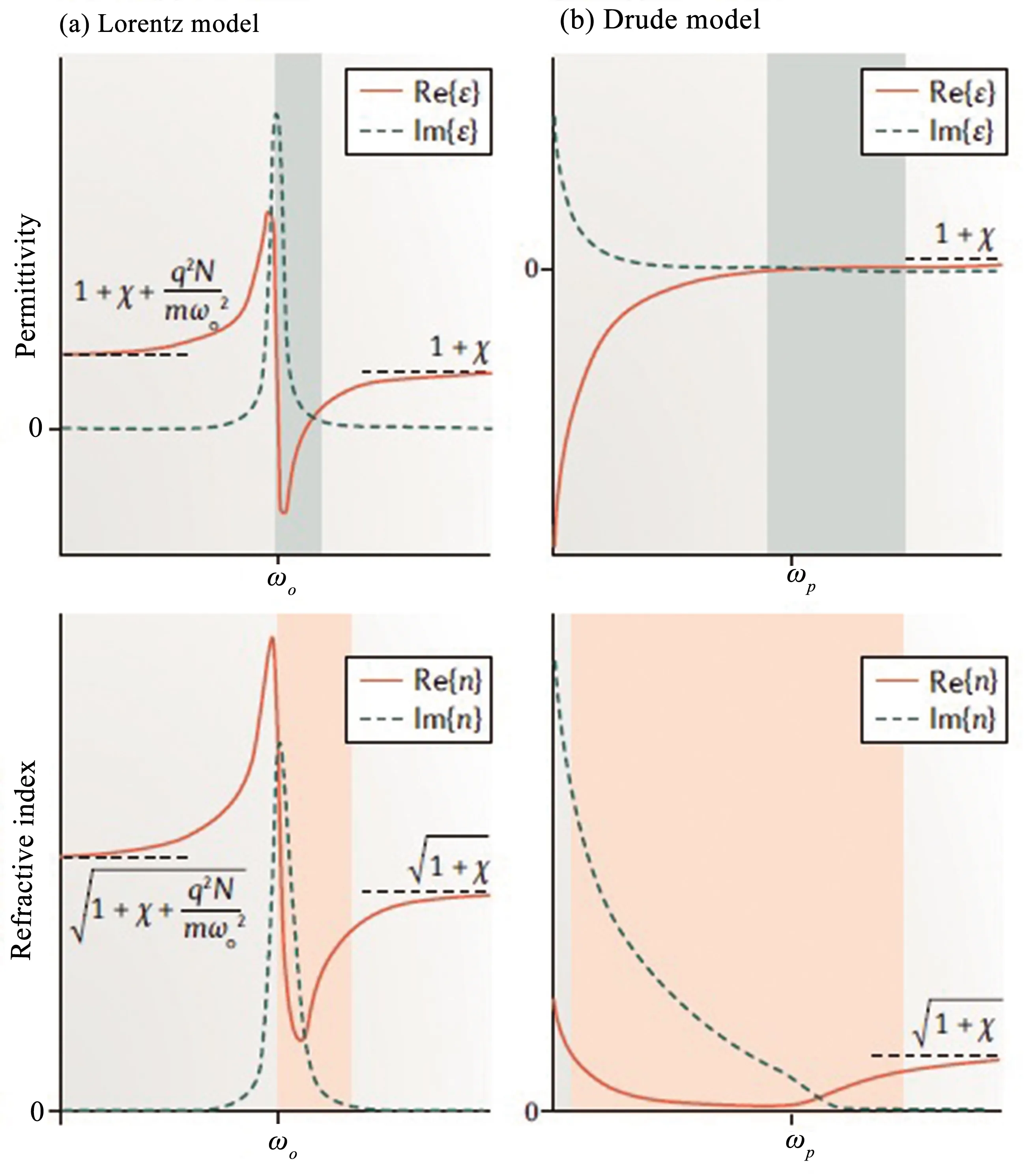
图1

最后，关于带间材料.如图1所示，介电率在洛伦兹共振的短波长边有一个谷，这个特征使得强共振和/或低背景介电的材料具有ENZ区域，且此区域预期在蓝光和紫外波段.比如，在拓扑绝缘体Bi1.5Sb0.5Te1.8Se1.2材料中，ENZ效应在紫外波段通过等离激元行为实现[86].尽管ENZ区域能够在带间材料中实现，但在共振处大的光学损耗却是一个很大的挑战.不过，ENZ区域大的光学损耗可能对增强光学吸收效应是有益的.

2.1.2 超材料 除了自然界中存在的材料外，人工构筑的超材料也可实现ENZ和NZI光学响应.典型的构型，比如金属与介电材料的堆叠[87-93]，如图2所示.在光频，介电材料具有正的介电常数，而金属具有负的介电实部，通过调控两种材料的权重比例可以在两者复合材料中实现EZN.在超构材料中实现EZN的结构还有很多，这里不做重点赘述.超构材料相对于自然材料有许多优势，比如近零波长及带宽可以通过控制材料的组分与结构实现极度的可调性，并且可以实现介电率与磁导率的同时可调，当然这些优点都是以显著增加的加工成本与复杂度为代价的.此外，需要特别指出的是，超材料的EZN或NZI行为仅为等效性质，发生在远大于结构单元的距离.

图2 Ag-SiO2金属-介电薄膜堆组成的ε近零(ENZ)超材料电镜图[87].

2.2ENZ材料非线性光学增强的机理克尔类型的光学非线性，即光致材料折射率的改变Δn与非线性折射率n2和光强I成线性关系，Δn=n2I.非线性折射率n2[94]可写为，n2=3χ(3)(ω;ω,ω,-ω)/4n0Re(n0)ε0c.其中，(3)为三阶非线性极化率，n0为线性折射率，ε0为真空介电常数，c为光速.从公式看，当分母上的Re(n0)为零时，n2是发散的.但上式的成立是有条件的，即|n2I/n0|≪1[95].显然，在低折射率介质中，用 上式描述非线性折射率是不适合的.光强相关的折射率应该直接写为，其中ε(1)为复线性介电率，|E|为材料内的光场幅度.此时，光致折射率的改变Δn为材料在高光强时的折射率与弱光强时折射率的差，而不需要等于n2I.上式光致折射率的改变必然是(3)的增强，或者|E|的增强，或者两者同时增强.ENZ材料的非线性光学增强机理目前主要有四种讨论.

2.2.1 三阶非线性极化率 上述讨论已经指出，非线性折射与(3)和|E|相关，非线性折射的增强必然由(3)的增强，或者|E|的增强，或者两者同时增强决定.首先，我们讨论ENZ下的(3).

2.2.2 电场连续引起的场增强 当表面没有电荷时，电位移矢量D在界面满足法向连续.因此，材料内的电场E法向分量大小正比于外电场大小E0，反比于材料的节电率，即|E⊥|∝ε-1|E0,⊥|.对于一束入射角为的p偏振入射光，电位移矢量法向连续，电场切向连续，|E⊥|∝ε-1|E0,⊥|,|E‖|∝|E0,‖|,|E0,‖|=|E0|cosθ,|E0,⊥|=|E0|sinθ，可得由此可以看出，在斜入射情况下，ENZ媒质中的电场远大于入射场.这种增强机理能够导致很多与角度显著相关的非线性光学效应.特别的，在薄膜ENZ材料中，相对于各向同性的ENZ材料，具有垂直表面方向(面外)为ENZ的各向异性材料，或称为纵向ENZ薄膜[27,100,101]，具有更大的强增强以及损耗不敏感特性.

2.2.3 EZN模式和Berreman 模式 EZN薄膜支持一系列独特的传播模式，包括无束缚布鲁斯特模，或称为Berreman 模式，以及在一些情况下的束缚模，或称为ENZ模[107].如前所述，ENZ模具有平的色散线型特征以及边界条件导致的强增强.但需要注意的是薄膜必须很薄(小于波长五十分之一)才能支持ENZ模式.比如ITO薄膜其ENZ波长大约在1240 nm，ITO薄膜厚度最多25 nm才能支持此模式，否则ENZ模退变为长程表面等离激元模式[108].像其他束缚模式一样，没有外在的耦合，ENZ模式在自由空间是很难达到的.

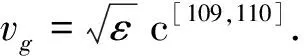
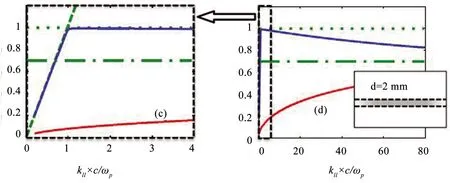
图3 当薄膜厚度减为2 nm时平带色散的ENZ模式[107].

3 ENZ材料非线性光学性质实验研究

基于ITO，AZO以及相关材料平台的非线性已被广泛实验研究.这里，我们主要综述实验测量ENZ中的一些非线性光学现象，如非线性折射率，超短脉冲下的谐波产生以及波混频，以及讨论存在静态电场时材料的行为以及其它非线性光学现象.

3.1光致折射率改变2016年，Boyd等人[11]在310 nm厚的ITO薄膜中的非线性折射率.利用z扫描方法在150 fs脉冲激光条件下，测得零介电波长(约1 240 nm)处的非线性折射率，在垂直入射时为n2=2.610-16m2/W.该值比偏离ENZ波长区域时的n2值大40倍.当p偏振入射光入射角为60o时，n2值达到1.110-14m2/W.最大饱和折射率改变达到0.72.泵浦探测实验表明，ITO薄膜非线性具有弛豫时间为360 fs的超快响应，且具有短于脉宽(150 fs)的上升沿时间[95].更深入详尽的分析表明，ITO薄膜中的非线性折射有来自三阶、五阶，甚至七阶的非线性贡献，如图4所示.2018年，Carnemolla等人[96]测量得到了AZO在其零介电波长(1 360 nm)处的非线性折射率n2=5.1710-16m2/W.该值比偏离零介电波长(1 400 nm)处的非线性折射率大35倍.大的非线性折射率还同样在有机ENZ薄膜中观察到[98].2018年，Lee等人[98]研究了55 nm厚的聚甲炔染料薄膜的非线性光学性质.该薄膜的EZN波长在可见光波段，约500 nm 至 570 nm.在EZN波长处，非线性折射率n2高达1.710-14m2/W，比非ENZ波长处的n2大两个量级.但是，该薄膜的损伤阈值比较低(小于45 GW/cm2)，远低于ITO和AZO(大于1 000 GW/cm2，有些情况下甚至可达2 000 GW/cm2[12])，使得其最大非线性折射率的改变受限.除薄膜外，2017年，Guo等人[113]利用化学合成的方法制备了直径约为8 nm的ITO纳米晶胶体.通过控制纳米晶胶体的浓度，可实现ENZ波长在1 300 nm至1 600 nm范围内可调.35 fs脉宽下，他们得到胶体的非线性吸收系数高达-5.1410-10m/W，并利用ITO纳米晶胶体的高饱和吸收系数，得到了脉宽是600 fs的锁模激光器.此外，在ENZ薄膜上制备超表面结构，可进一步增强其非线性折射率.2018年，Boyd等人[114]在ITO薄膜表面制备了金棒(360 nm110 nm30 nm)做为纳米天线来辅助阻抗匹配和场增强.纳米天线在ENZ波长1 240 nm附近产生表面等离激元共振，可提供50 倍的激光峰值强度增强.另外，在垂直入射时，天线还可以有效的将光从自由空间耦合进ITO薄膜.这种复合超表面结构显示出巨大的非线性折射率|n2|=3.7310-13m2/W，同时，非线性的带宽也显著增大超过400 nm.总的折射率改变Δn大于2.5，且响应时间只有纯ITO薄膜的50%.当然，这种超表面构型也有其缺点，主要受限于金纳米天线的损伤阈值[115].

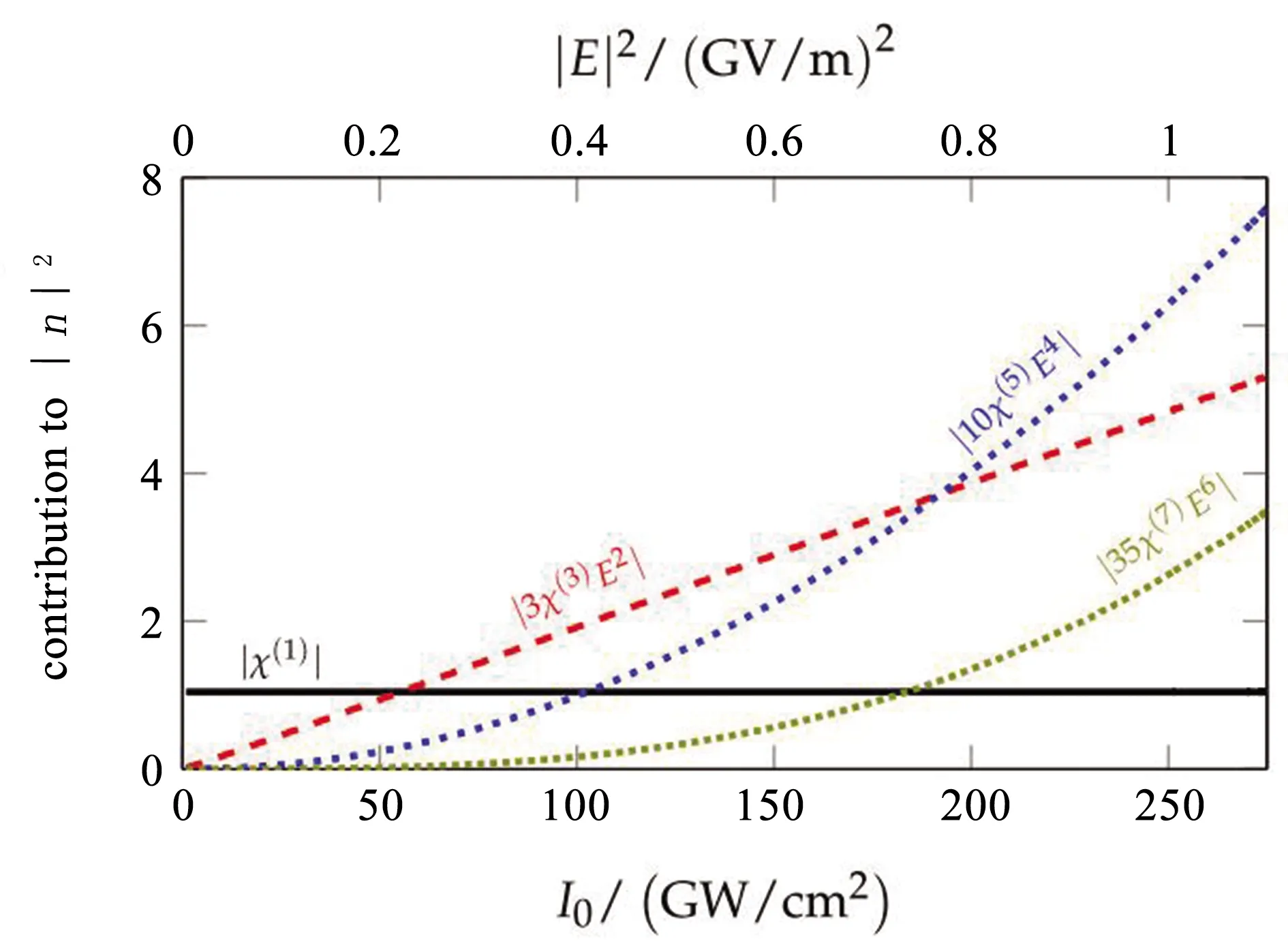
图4 ITO中折射率随光强变化[95]

3.2谐波产生在实验测量ENZ材料的谐波产生之前，已经有许多的理论工作预言了ENZ和NZI材料[25,27,29,116]中的谐波产生增强.最近，关于ENZ材料中谐波产生的微观理论模型[101,117,118]也陆续提出，尤其是ITO共振体系在ENZ条件下由自由电子产生的二次谐波产生(SHG)和束缚电子贡献的三次谐波产生(THG)理论[119].

2015年，Luk等人以及Capretti等人[9,10]独立报道了ITO中THG在零介电波长处的增强.Luk等人[94]在脉冲宽度为150 fs，峰值光强为40 MW/cm2的激光条件下，测量了37 nm厚的ITO薄膜中的THG.研究工作表明，在零介电波长处，THG在ITO薄膜中的转换效率是在300m厚的单晶硅中的600倍，并得到为3.510-18m2/V2.Capretti等人[9]在脉宽50 fs，峰值光强20 GW/cm2条件下研究了33 nm厚的ITO薄膜的THG.结果发现，在Kretchsmann构型下，ITO薄膜零介电波长处的THG信号是常规斜入射测量时的200 倍.这主要归因于Kretchsmann构型下形成的EZN模式比常规斜入射测量时薄膜中的光强增强6倍，因此THG强度增强200倍.THG的转换效率约为3.3约为310-21m2/V2.ITO中大的三阶非线性极化率归因于大的电子迁移速率.

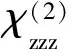
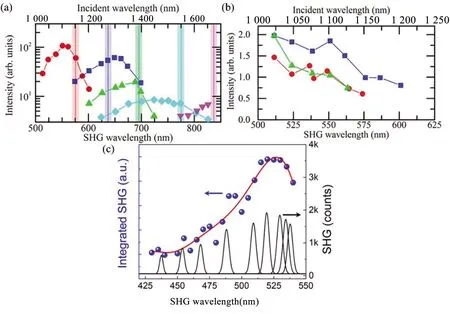
图5 ε近零材料的谐波产生

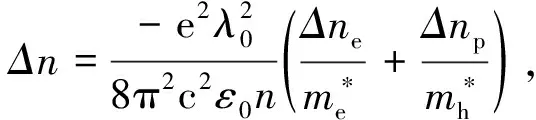
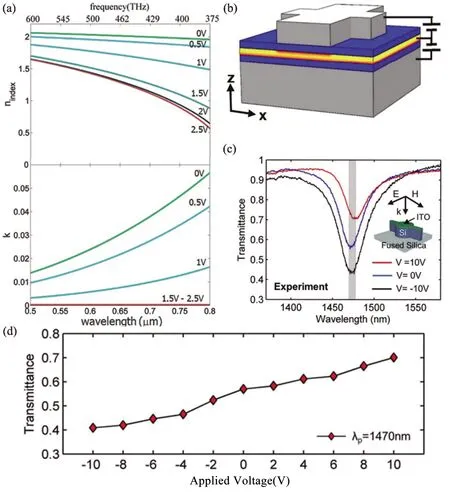
图6

3.4其他非线性现象除了上述非线性折射率及谐波产生的增强，ENZ和NZI还可以实现许多其他非线性光学效应.我们将针对几个典型研究工作做简要概述.

2017年，Yang等人[13]研究了75 nm 厚的In:CdO 薄膜(ENZ波长约为2100 nm)中的偏振开关效应，消光比达到20 dB，如图7所示.ENZ薄膜的Berreman模式起到表面等离激元腔的作用，比单纯通过薄膜的吸收增强了14倍.2018年，Taghinejad等人[124]研究了用10 nm厚ITO薄膜间隔金膜与金纳米结构阵列的偏振光开关.在p偏振光照射时的共振腔模式下，这种结构具有显著的偏振相关的响应.波长为645 nm 共振泵浦时，反射率的最大相对改变ΔR/R 达到75%.2017年，Kim等人[125]研究了70 nm厚的主动可调的ENZ层Fabry-Perot腔的共振，共振波长的可调范围达到200 nm.这种可调特性主要归因于ENZ等离子体频率的可调行，可以从1.85 eV调到1.70 eV.

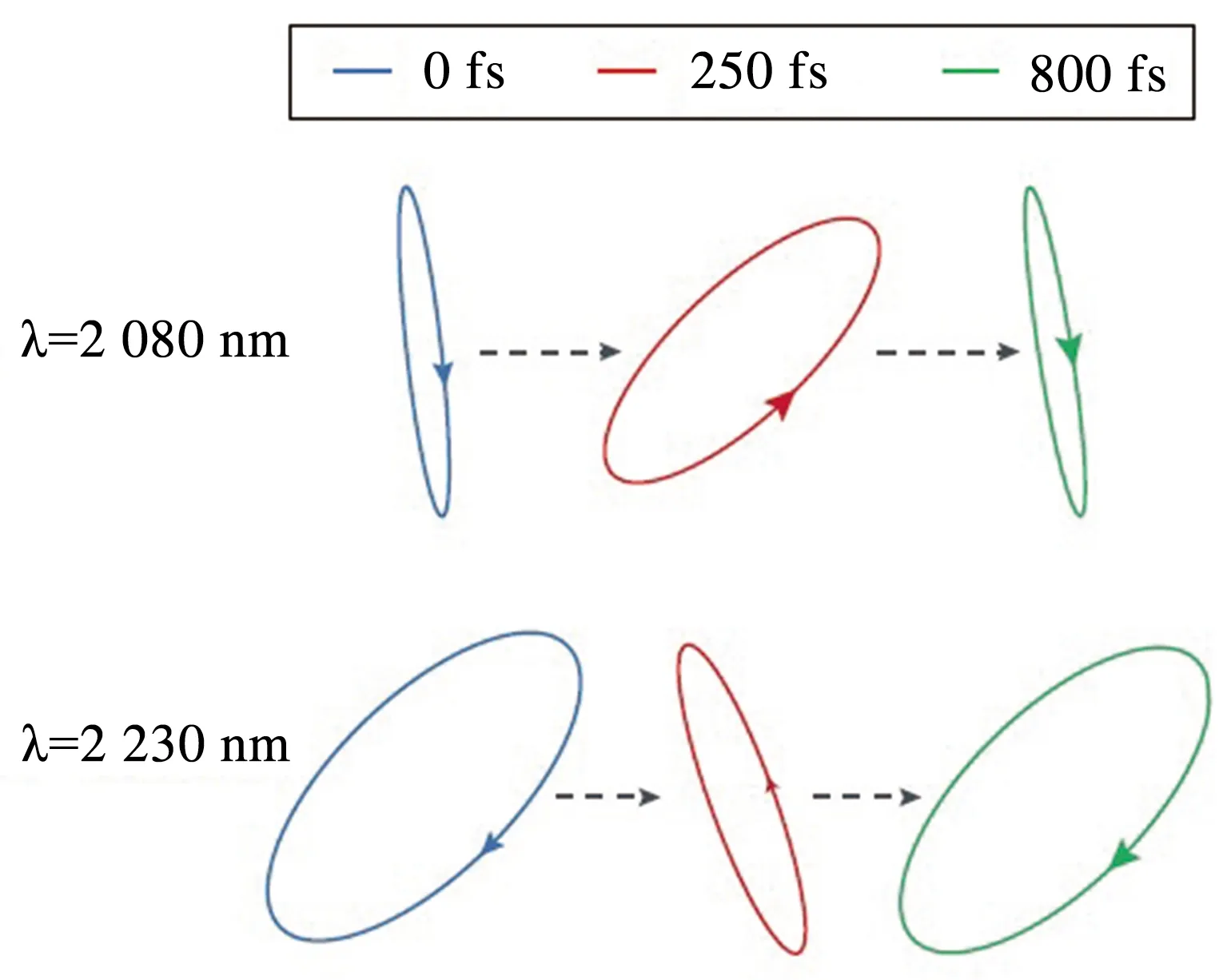
图7

最后，NZI材料还提供了实现非线性相位匹配的优异特性.一束光场通过折射率为零的材料具有无方向性的k矢量(k=0).因此，非线性相互作用光束可以在任意方向相互混合从而满足相位匹配条件.2013年，Suchowski等人[126]研究了800 nm厚的渔网结构的超材料四波混频.此结构的零折射率波长为 1 340 nm 和1 460 nm.实验发现，在入射光波长接近零折射率波长时，前向传播的非线性产生信号光和后向传播的非线性产生信号光强度大概相同，表明前向信号光和后向信号光同时满足相位匹配条件，不同于传统当前向信号光满足相位匹配条件时，后向光不满足相位匹配而较弱的情况.2014年，Mattiucci等人也从理论上预言了在狄拉克锥零折射率超材料中的二次谐波产生[127]和四波混频过程具有相似的效应[99].值得注意的是，在NZI介质中的非线性作用的相位匹配条件仍然是必须满足的，只是，在NZI条件下，在多重方向上入射或出射的光可以同时满足相位匹配条件.

4 结 语

我们综述了目前在ENZ和NZI响应下的各种非线性光学效应.实验结果表明，ENZ材料确实可以显著提高超快的非线性效应，比如强度相关的折射率[11，96，98]以及谐波产生[9，10，34]等.尽管ENZ材料已经使超快非线性光学效应进入了一个新的领域，但ENZ从实验室概念到实际应用仍有许多工作需要做.其中，考虑体相ENZ材料时，一个主要障碍是关于材料工程，即不像硅在电子学中的地位，目前还没有一种材料当担当唯一性的ENZ非线性材料角色.尽管目前多数的研究都集中在ITO和AZO上，但这两种材料也有明显的局限性，比如光学损耗问题和制备过程中低重复率的问题.因此，更好的材料还需要探索.理想的ENZ材料应具有以下几个性质：CMOS工艺兼容性，高度结晶性，大的载流子迁移率及低的线性损耗.同时，这种材料应具有可剪裁的零介电波长，能够直接被沉积制备或形成纳米结构.目前，还没有发现满足上述所有标准的材料.因此，在发展用于实际可用的以及低成本非线性光学器件的ENZ材料方面还需要付出很大努力.另外，还有一些不同非线性响应时机理问题有待解决，比如，在ENZ区声子是否同样增强非线性响应；热电子效应是否与脉宽相关；脉宽对非线性与ENZ带宽的影响；以及在零介电情况下，其他非线性效应是否也如强度相关的折射率一样需要修正描述方程等.最后，一些理论预测，比如在ENZ和NZI材料中的自由腔阻光以及具有孤子解的光束自陷，[112，128]ENZ材料中的自发辐射以及超辐射增强[129,130]，通过调制Purcell效应[131]控制自发辐射等问题还需要实验验证.

尽管在此领域还存在上述提到的问题和挑战，我们看到ENZ非线性材料在纳米光子学和非线性光学方面的应用前景还是非常激动人心的.随着该领域继续深入研究以及材料制备与微加工技术的进步，我们期望在ENZ材料非线性光学响应的研究会在近几年产生非常重要的结果.