分布时滞区间神经网络的脉冲同步控制

王 瑶 田玉娟

(山东师范大学数学与统计学院, 250358, 济南)

1 引 言

近年来,随着信息科学、神经科学和控制科学的快速发展,神经网络在图像处理、联想记忆、模式识别、自动控制等众多领域得到了广泛应用[1-4].神经网络也随之得到了深入的研究.由于两个相互作用的神经元自身之间不可避免地存在传递信息所需的时间以及物理元器件的限制,在神经网络的应用中会产生时滞的现象.时滞的存在对神经网络的稳定性具有较大的影响,可能导致振荡行为、性能劣化、甚至混沌现象[5-8].因此研究有延迟的神经网络的动力学行为尤为重要.同步作为一种重要的动力学行为,在生物系统、信息科学和安全通信等领域有着广泛应用[9-11].

到目前为止,针对如何实现神经网络的同步有很多控制方法,如间歇控制[12]、脉冲控制[13]、反馈控制[14]、采样控制[15]等.脉冲控制作为一种典型的不连续控制方法,在降低控制成本和信息传输量上具有很大的优势,并已应用于药物给药,水生生态系统的治理以及种群模型等诸多实际问题.近年来,大量的文献通过脉冲控制方法来研究神经网络的同步[16-19].He W L等人[16]基于脉冲控制研究了时滞神经网络的牵制控制同步；Kan Y等人[17]研究了具有时变时滞的复值神经网络在脉冲控制下的指数同步.然而,在现实生活中,可用的信息通常是不确定的、不精确的,这些数据都是通过区间数据或模糊数据表示出来的.所以在很多应用中应该将输入向量和预测值用区间形式表示,而不是单个实值表示.因此,区间神经网络的研究是一个十分重要的课题,很多学者对时滞区间神经网络的动力学行为进行了研究[20-23].但其所研究的时滞大多局限于离散时变时滞情形.由于具有大量的并行通道,神经网络往往具有空间属性.因此,有必要在区间神经网络中引进分布时滞,以使它们更精确地贴合系统本质.Li X等人[24]究了具有中立型连续分布时滞的随机区间神经网络的全局鲁棒稳定性；Jiang F F等人[25]研究了具有时变时滞和分布时滞的区间神经网络在脉冲扰动下的平稳振荡.尽管许多文献已经研究了具有分布时滞的区间神经网络的动力学行为,但很少有人运用脉冲控制来实现区间神经网络的同步.

基于以上分析,本文将进一步研究具有分布时滞的区间神经网络在脉冲控制下的同步问题.通过构造Lyapunov函数,利用脉冲微分不等式技术，导出依赖于分布时滞的全局指数同步准则,所得判据均由线性矩阵不等式表示.最后,通过一个数值算例验证该结论的正确性.

2 预备知识

2.1符号介绍

1)R表示实数集；Rn表示n维欧几里得空间；Z+表示正实数集；‖·‖为欧几里得范数；

2)A>0(A<0)表示A为正定(负定)矩阵；AT表示矩阵A的转置；A-1表示矩阵A的逆；

3)λmax(A)(λmin(A))表示矩阵A的最大特征值(最小特征值)；

4)PC(J,U)表示定义域为J⊆R,值域为U⊆Rk(1≤k≤n)的分段连续函数；

5)I表示适合维数的单位矩阵；

6)*表示矩阵中的对称部分；Λ={1,2,…,n}.

2.2系统模型考虑具有分布时滞的区间神经网络

(1)

其中x(t)=(x1(t),…,xn(t))T∈Rn为系统在t时刻的状态向量；f(x(t))=(f1(x(t)),…,fn(x(t)))T∈Rn是神经网络激活函数；C=diag(c1,…,cn)∈Rn×n是一个正对角矩阵,A,B∈Rn×n为连接权矩阵；J(t)∈Rn是外部输入函数；β(t)是分布时滞，且满足条件0≤β(t)≤β,其中β为常数；φ(·)∈PC([-β,0],Rn)为初值条件.

假设1对任意的u,v∈R，存在一个正对角矩阵L=diag(L1,…,Ln),使得下列不等式成立

‖fi(u)-fi(v)‖≤Li‖u-v‖,i∈Λ.

假设2令系统中未知矩阵C,A,B在下列区间内有界

C∈CI,A∈AI,B∈BI,

其中

与驱动系统(1)相对应的响应系统为

(2)

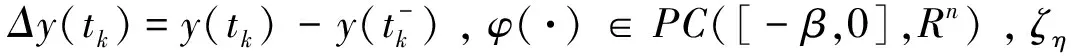
令e(t)=y(t)-x(t)表示同步误差,可得误差系统

(3)

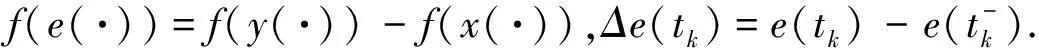
其中C0,A0和B0分别是区间矩阵C,A和B的参考矩阵.令

其中ei∈Rn,i∈Λ表示i行为1,其他元素为0的列向量.系统(3)可以重新表示为

(4)

其中

Θ=[Θ1,Θ2,Θ3]n×3n2,Δi∈Γ,i=1,2,3,

定义1[17]若存在常数μ>0,N>1使得下列不等式成立

则驱动系统(1)和响应系统(2)在脉冲集合ζη下是全局指数同步的.

引理1[26]考虑如下脉冲微分不等式

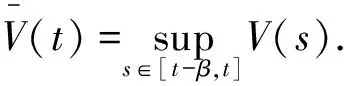
其中M>1,λ>0.

引理2[27]对任意正定矩阵E∈Rn×n,常数a>0,b>0,定义向量函数u:[a,b]→Rn,则有

引理3[28]对任意向量x,y∈Rn和正定矩阵Q∈Rn×n,有下列不等式成立

xTy+yTx≤xTQx+yTQ-1y.

3 主要结果

定理1在假设1和2下,如果存在常数a∈R,b>0,0<ε<1,和正定矩阵P∈Rn×n,正定对角矩阵Qi∈Rn×n(i=1,2),Qi∈Rn2×n2(i=3,4,5),矩阵Zk∈Rn×n使得下列不等式成立

(5)

(6)

(7)

其中

则驱动系统(1)和响应系统(2)关于脉冲序列ζη是全局指数同步的,且控制增益为Ek=P-1Zk.

证选取Lyapunov函数V(t)=eT(t)Pe(t),沿着系统(4)的轨迹取V(t)的导数,当t∈[tk-1,tk)，k∈Z+时,可以推导出

(8)

由(8)式和引理3,可得

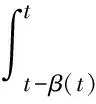
(9)

由Ψe(t)定义知

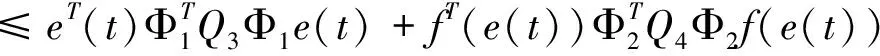
(10)

由引理3和(10)式，有

(11)

结合(8)式和(11)式，可以得出

(12)

在条件(6)下,由引理2得

(13)

结合条件(5)、(6)、(12)和(13),可得

另一方面，当t=tk时，可得

V(tk)=eT(tk)Pe(tk)

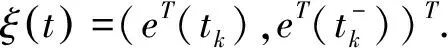
其中M>1,λ>0.由于V(t)=eT(t)Pe(t),可得

综合各式可得

因此,系统(1)和(2)关于脉冲序列ζη是全局指数同步的.

注1定理1通过构造Lyapunov函数研究了区间神经网络的同步问题,给出了依赖于分布时滞的全局指数同步准则.近年来,有关区间神经网络的研究成果越来越丰富,但关于区间神经网络的脉冲控制相关结果较少.文献[20]和[21]研究了时滞区间神经网络的动力学行为,但它们所考虑的时滞仅限于时变时滞且都忽略了分布时滞的影响.因此,本文的研究改进了文献[20]和[21]的结果.

特别地，若C,A,B是已知的常数矩阵，则有下列推论1成立.

推论1在假设1下,如果存在常数a∈R,b>0,0<ε<1,和正定矩阵P∈Rn×n,正定对角矩阵Qi∈Rn×n(i=1,2),矩阵Zk∈Rn×n使得下列不等式成立

(14)

bP-β2LQ2L>0,

(15)

(16)

其中

Π11=-2PC-aP+LQ1L,

则驱动系统(1)和响应系统(2)关于脉冲序列ζη是全局指数同步的,且控制增益为Ek=P-1Zk.

4 数值算例

本节通过一个数值例子来说明所得结果的有效性和优越性.

例1考虑二维区间神经网络(1),参数如下：

系统初值条件如下：φ(t)=(0.3,1.6)T,激活函数f(x)=tanh(x),分布时滞β(t)=0.3-0.01sin(t),脉冲区间tk+1-tk=0.005 4，外部输入J=(0,0)T.

同理，响应系统(2)选取初值条件φ(t)=(-1.9,-2)T.另一方面，基于以上参数，可得L=I2×2,

令a=15,b=0.5,ε=0.07，基于定理1,使用Matlab LMI工具箱,可得

因此,增益矩阵设计如下

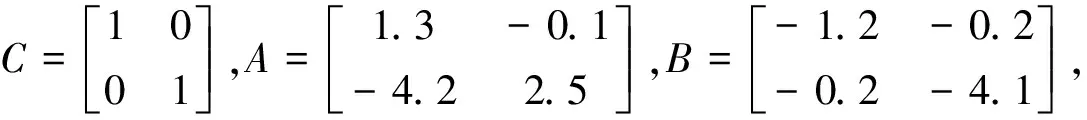
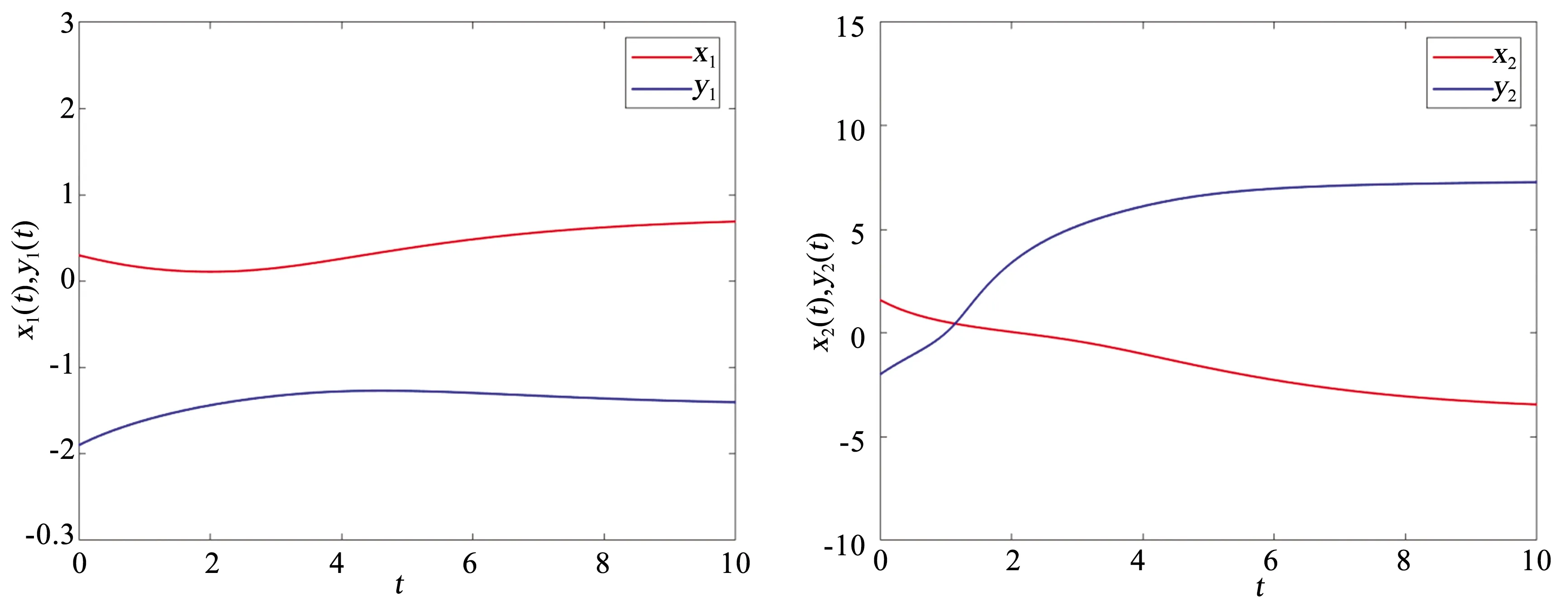
图1 无脉冲控制时驱动系统(1)和响应系统(2)的状态轨迹

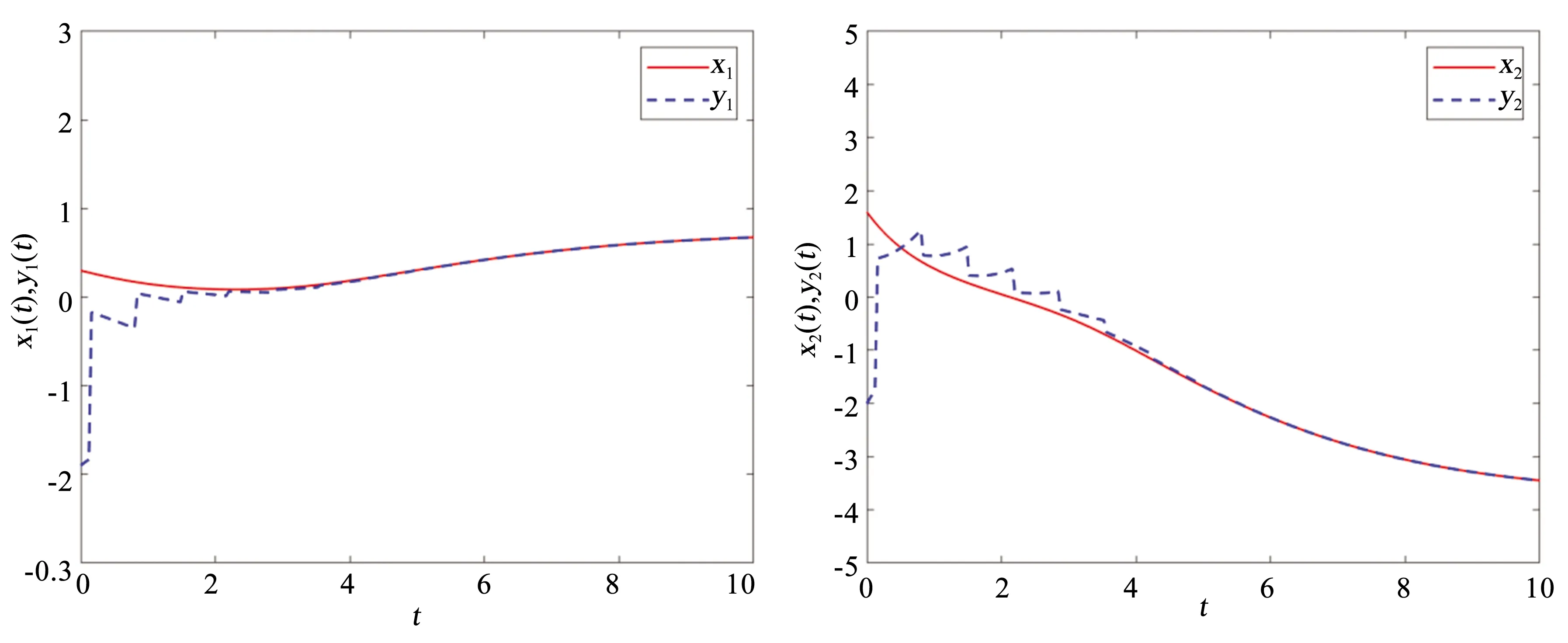
图2 在脉冲控制下驱动系统(1)和响应系统(2)的状态轨迹

5 结 语

本文考虑了具有分布时滞的区间神经网络在脉冲控制下的同步问题.通过构造Lyapunov函数,利用脉冲微分不等式技术,得到了驱动系统和响应系统全局指数同步的充分条件,并得到了相关推论.最后给出了一个数值算例,验证了所设计方案的可行性和有效性.