响应变量缺失下基于协变量平衡下的变系数模型的经验似然推断

范 莉 王秀丽

(山东师范大学数学与统计学院，250358，济南)

1 引 言

考虑如下形式的变系数模型

Y=XTβ(U)+ε，

(1)

其中，Y是响应变量，X,U为协变量，X∈RP，U∈R，β(·)=(β1(·)，…，βp(·))T为一个p维未知的参数函数向量，ε为误差项且满足：E(ε|X,U)=0，var(ε2|U,X)=σ2(U).

这里主要考虑响应变量Y随机缺失的情况，样本量为n的不完全数据可以表示为(δi,Xi,Yi,Ui),i=1,…,n，其中当Yi缺失时，δi=0,否则δi=1，且满足

P{δi=1|Yi,Xi,Ui}=P{δi=1|Xi,Ui}=π(Xi,Ui).

(2)

变系数模型是一类应用非常广泛的模型，包含了常见的一些模型，如可加模型，部分线性模型，单指标函数系数回归模型等.它不仅避免了“维数祸根”，而且更加具有可解释性，许多统计学者对该模型进行了研究，取得了丰富的研究成果.Fan J Q等人[1]提出了两步估计法，允许系数函数有不同的窗宽，并且证明了两步估计要优于一步估计.卢一强等人[2]考虑到各个系数函数的差别，允许各个系数函数有不同的光滑参数，在系数函数为三阶B样条函数的条件下，用贝叶斯模型平均的方法来估计函数系数.

但在实际问题中经常会遇到缺失数据，分析缺失数据广泛使用的是由Thompson P G等人[3]提出的逆概率加权方法，这个方法产生的估计在缺失机制假定正确的前提下是无偏的.杜海燕等人[4]考虑了协变量缺失下变系数部分非线性模型的统计推断问题，基于逆概率加权利用轮廓最小二乘和经验似然的方法得到参数和非参系数的估计.陈盼盼等人[5]基于逆概率加权最小二乘方法研究了缺失数据下变系数部分线性模型的统计推断问题.但是这种估计方法也只是用到了完全观测的数据.为了提高估计的效率，Robins J M等人[6]提出了扩张的逆概率加权(Augmented Inverse Probability Weighting，AIPW)，通过对每一个缺失的变量借补一个合适的值，利用观测到的数据和借补的值进行统计推断，得到的估计量具有双稳健性.有很多学者利用它来处理缺失数据的问题[7-9].在运用以上两种方法构造估计量时，通常需要先估计出选择概率，当选择概率模型和回归模型都被指定正确时，扩张的逆概率加权就会得到很好的估计，但是当两者都被指定错误时，扩张的逆概率加权方法的双稳健性就会变差.为了解决这个问题，Kosuke I等人[10]提出了协变量平衡倾向得分(Covariate Balancing Propensity Score，CBPS)方法，这个方法通过最大化协变量平衡得到的参数值来降低潜在的选择概率模型被错误指定而导致的后果，所以这是一种稳健的估计选择概率的方法.Guo D L等人[11]基于协变量平衡倾向得分(CBPS)研究了非线性模型稳健估计，但对于变系数模型中的稳健估计没有进行研究.本文将基于协变量平衡倾向得分研究在响应变量随机缺失条件下的变系数模型的经验似然统计推断.

2 基于协变量平衡倾向得分的估计量的构造

在(2)式中π(Xi,Ui)是未知的，通常情况下假设π(Xi,Ui)是logistic模型,则有

(3)

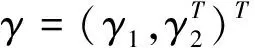
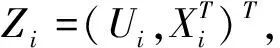
(4)

若π(Z，γ)关于γ是二阶连续可导的，则(4)式等价于如下一阶条件

(5)

其中π′(Zi,γ)=∂π(Zi,γ)/∂γT.

虽然极大似然方法简单，但是当选择概率错误的时候，该方法得到的回归系数估计量是有偏的.为了使参数方法更稳健，利用文献[10]提出的协变量平衡的倾向得分(CBPS)方法对选择概率模型中的未知参数γ进行估计，即令选择概率π(Zi,γ)满足协变量平衡条件

(6)

即使选择概率模型被指定错误，(6)式也能保证协变量的一阶矩平衡，由(6)式可得协变量平衡条件的样本形式为

(7)

若只考虑(5)式，此时参数的个数和方程的个数相等即为恰好识别,这种情况下利用矩方法的思想可以得到未知参数的矩估计.在这里只考虑过识别的情形，联合(5)式及(7)式可得

(8)

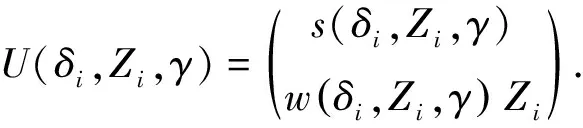
(9)

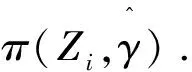
为了方便介绍，引入以下的记号和假设条件.

C1 对所有Zi，π(Zi,γ)在γ0附近都是一个已知可微的函数；

C2E(Zi)、E[W(δi,Zi,γ)]存在且矩阵E(ZiZiT)满秩；

C3 1)WE[U(δi,Zi,γ)]=0当且仅当γ=γ0，γ0∈Θ为紧集；

2)E(‖π′(Z，γ0)‖2)<且E(‖Zi‖2)<；

C4U有有界支撑Ω，且U的密度函数f(u)>0，f(u)为Lipschitz连续；

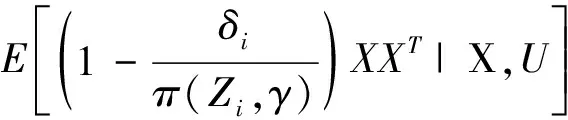
C6 核函数K(·)为有界支撑的对称概率密度函数；

C7 {β(U)，i=1,2,…,p}在所有的U∈Ω有连续的二阶导数；

C8 存在r>0，使得E|X|2+r<,E|ε|2+r<；

C9 窗宽h满足当n→，h→0时,nh5→0,nh→；

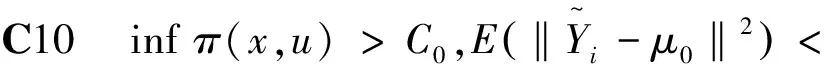
由参考文献[13]，可以得到下述的定理1.

定理1[13]假设Zi，i=1,2,…,n是一组独立同分布的随机向量，满足条件C1-C3,γ0为γ的真值，则有

推论1[13]如果π(Zi,γ)是连续的，γ0为γ的真值，在条件C1-C3下，有

2.2回归系数的经验似然由Zhou X S等人[14]的研究结果可知，系数函数向量β(u)=(β1(u),β2(u),…,βp(u))T在u0处的局部线性估计可表示为

其中，IP和0p分别表示p阶单位矩阵和p阶零矩阵，

Y=(Y1,Y2,…,Yn)T，X=(X1，X2，…，Xn)T，ε=(ε1，…，εn)T，

W(u0)=Diag(Kh(U1-u0)δ1,Kh(U2-u0)δ2,…,Kh(Un-u0)δn)，

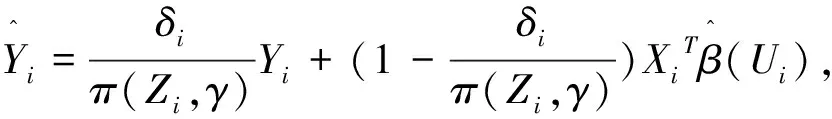
(10)

构造辅助随机向量

(11)

(12)

利用Lagrange乘子法选择最优pi，可得

(13)

其中λ为拉格朗日乘数且为下述方程的解

(14)

定理2如果假设条件C1-C10成立，则当β(u)为真值时，有

其中χp2表示自由度为p的卡方分布.

基于定理2可以定义β(u)的近似置信水平为1-α的置信区间为

Iα(β(u))={β(u)|l(β(u))≤χp2(1-α)}.

3 定理的证明

下面给出定理2的证明，首先给出如下的引理1.

引理1若假设条件C4-C10成立，则有

其中

证经计算有

类似于文献[11]中定理2，可证

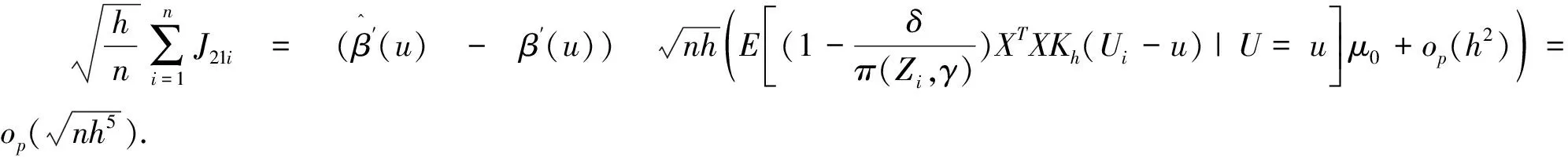
下面给出定理2的证明.

证由引理1的证明简单计算可得

(15)

由引理1的证明及文献[15]中引理1的证明可得

(16)

类似于文献[16]中的定理2的证明可知

λ=OP((n/h)-1/2).

(17)

由(15)式和(16)式，将(13)式进行Taylor展开易得

(18)

又由(14)式，结合(15)-(17)式，可得

(19)

(20)

再根据(18)-(20)式,计算可知

结合引理1，定理2得证.