一道竞赛题的多证、多变与几何背景
2021-11-10 06:20:16云南省昆明市第一中学650000张远雄
中学数学研究(江西) 2021年10期
云南省昆明市第一中学 (650000) 张远雄
本文对一道法国数学奥赛试题进行证明,然后得到它的五种变式,最后探讨该不等式的几何背景.

不等式简洁、优美,下面笔者从三个视角对这道不等式进行探究.
视角1证法探究
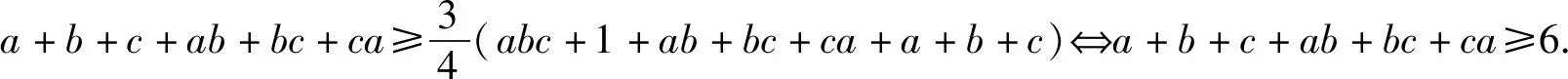

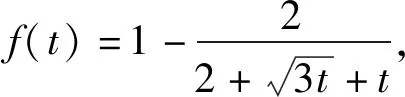




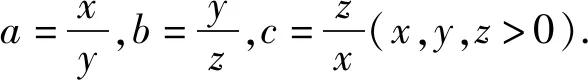

视角2不等式的多变
由上述证明过程,可获得如下变式:

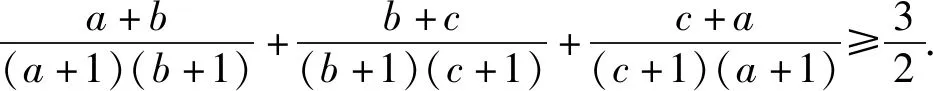

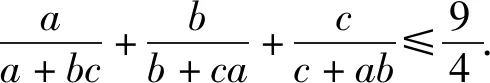

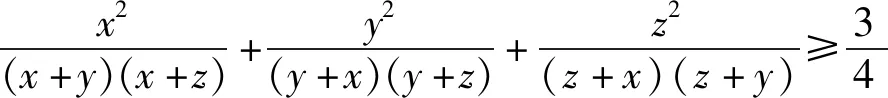
视角3不等式的几何背景
由a,b,c为正数,且abc=1,可以联想到三角形的塞瓦定理:

图1

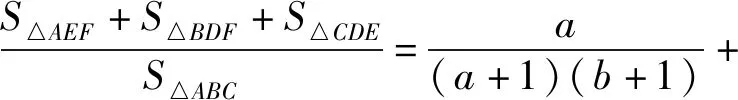

在上述探究的基础上,我们还可以继续探究获得更多的优美不等式,也可以将以上这些关于三元(a,b,c)的不等式拓展到四元(a,b,c,d)甚至n元的情形.其实,我们的探究并没有结束,限于篇幅,这里不再赘述.
猜你喜欢
中学数学研究(2024年3期)2024-04-05 16:02:32
中等数学(2022年4期)2022-08-29 06:27:14
中等数学(2020年7期)2020-11-26 08:03:46
天府数学(2020年3期)2020-09-10 19:53:46
中等数学(2020年4期)2020-08-24 08:08:38
河北理科教学研究(2020年1期)2020-07-24 08:14:34
中等数学(2019年5期)2019-08-30 03:52:22
福建中学数学(2018年5期)2018-11-29 07:24:48
科教新报(2018年14期)2018-06-24 10:32:01
数学学习与研究(2016年1期)2016-07-04 13:18:37

