两道三角形最小值问题的解法探究
2021-11-10 06:19:32广东省惠州仲恺中学516029黄国春
中学数学研究(江西) 2021年10期
广东省惠州仲恺中学 (516029) 李 林 黄国春
近日,笔者对如下两道三角模考试题产生很大兴趣,这两道问题都是条件式求最小值问题,笔者对其给出几种解法,供大家学习.



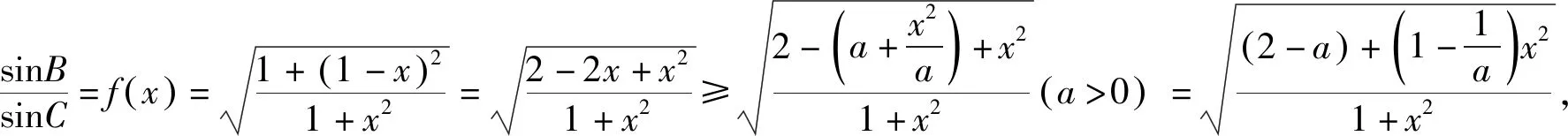
评注:解法1运用对勾函数求最小值,解法2用待定系数法求最小值.

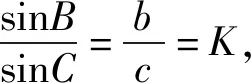

本题对学生(甚至部分老师)来说有点难度,难的原因有两个:一是有关角度的条件式看着比较复杂,变形方向比较多,不知道从哪里入手;二是两个已知条件之间看着似乎没有联系,并且两个条件和目标式之间也联系得不紧密,换言之,难以找到三者之间的桥梁.
很多人可能就是简单地把sin(A-B)拆开之后合并同列项,然后利用正弦定理和余弦定理得到a,b,c之间的关系,实际上,既然拆开之后出现sinA和sinB的齐次式,利用正弦定理可以得到a与b的关系,得到c与b的关系呢?这样就和目标式成功地联系上了.


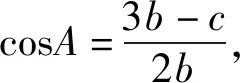
猜你喜欢
农业工程学报(2023年5期)2023-05-15 03:30:56
旅游纵览(2022年5期)2022-06-01 22:37:21
汽车实用技术(2022年7期)2022-04-20 11:45:06
中学数学研究(广东)(2021年11期)2021-07-08 11:46:04
中学生数理化(高中版.高二数学)(2020年11期)2020-12-14 07:36:32
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27 03:04:28
河北理科教学研究(2020年1期)2020-07-24 08:14:28
音乐教育与创作(2020年4期)2020-05-13 13:49:58
水动力学研究与进展 B辑(2017年3期)2017-06-07 08:22:46
智富时代(2017年4期)2017-04-27 02:13:48

